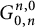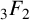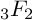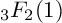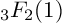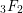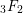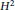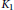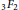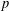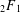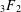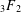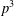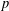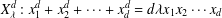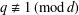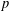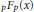Refine search
Actions for selected content:
22 results
TRANSFORMATION FORMULA OF DWORK’S p-ADIC HYPERGEOMETRIC FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1-12
-
- Article
- Export citation
THE WZ METHOD AND FLAWLESS WZ PAIRS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-9
-
- Article
- Export citation
An approximation formula for the shifted cubic moment of automorphic L-functions in the weight aspect
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 06 September 2023, pp. 715-738
- Print publication:
- June 2025
-
- Article
- Export citation
Riesz-type criteria for L-functions in the Selberg class
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1062-1088
- Print publication:
- June 2024
-
- Article
- Export citation
Generating function of multiple polylog of Hurwitz type
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 November 2022, pp. 1-17
- Print publication:
- February 2024
-
- Article
- Export citation
OHNO–ZAGIER TYPE RELATIONS FOR MULTIPLE t-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 215-226
- Print publication:
- April 2023
-
- Article
- Export citation
EVALUATION OF CERTAIN EXOTIC
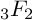 $_3F_2$(1)-SERIES
$_3F_2$(1)-SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 107-118
- Print publication:
- March 2023
-
- Article
- Export citation
A note on the number of irrational odd zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 09 October 2020, pp. 1699-1717
- Print publication:
- August 2020
-
- Article
- Export citation
Hypergeometric rational approximations to ζ(4)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 374-397
-
- Article
-
- You have access
- Open access
- Export citation
AN ALGEBRO-GEOMETRIC STUDY OF SPECIAL VALUES OF HYPERGEOMETRIC FUNCTIONS
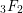 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 13 September 2018, pp. 47-62
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
On extensions of van Hamme's conjectures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 30 August 2018, pp. 1017-1027
- Print publication:
- October 2018
-
- Article
- Export citation
SOME HYPERGEOMETRIC INTEGRALS FOR LINEAR FORMS IN ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 372-375
- Print publication:
- December 2018
-
- Article
-
- You have access
- Open access
- Export citation
CM Periods, CM Regulators, and Hypergeometric Functions, I
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 3 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-514
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
SUPERCONGRUENCES INVOLVING
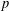 $p$ -ADIC GAMMA FUNCTIONS
$p$ -ADIC GAMMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 27-37
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
COUNTING POINTS ON DWORK HYPERSURFACES AND
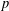 $p$ -ADIC HYPERGEOMETRIC FUNCTIONS
$p$ -ADIC HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 208-216
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Mahler Measures as Linear Combinations of L–values of Multiple Modular Forms
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 424-449
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Bounds for zeros of Meixner and Kravchuk polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 47-57
-
- Article
-
- You have access
- Export citation
Densities of Short Uniform Random Walks
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 5 / 01 October 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-990
- Print publication:
- 01 October 2012
-
- Article
-
- You have access
- Export citation
A Generalised Kummer-Type Transformation for the pFp (x) Hypergeometric Function
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 3 / 01 September 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 571-578
- Print publication:
- 01 September 2012
-
- Article
-
- You have access
- Export citation
ANALYTIC PROPERTIES OF MIRROR MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 195-235
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation