Article contents
Mahler Measures as Linear Combinations of L–values of Multiple Modular Forms
Published online by Cambridge University Press: 20 November 2018
Abstract
We study the Mahler measures of certain families of Laurent polynomials in two and three variables. Each of the known Mahler measure formulas for these families involves 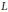 $L$ –values of at most one newform and/or at most one quadratic character. In this paper we show, either rigorously or numerically, that the Mahler measures of some polynomials are related to
$L$ –values of at most one newform and/or at most one quadratic character. In this paper we show, either rigorously or numerically, that the Mahler measures of some polynomials are related to 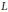 $L$ –values of multiple newforms and quadratic characters simultaneously. The results suggest that the number of modular
$L$ –values of multiple newforms and quadratic characters simultaneously. The results suggest that the number of modular 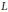 $L$ –values appearing in the formulas significantly depends on the shape of the algebraic value of the parameter chosen for each polynomial. As a consequence, we also obtain new formulas relating special values of hypergeometric series evaluated at algebraic numbers to special values of
$L$ –values appearing in the formulas significantly depends on the shape of the algebraic value of the parameter chosen for each polynomial. As a consequence, we also obtain new formulas relating special values of hypergeometric series evaluated at algebraic numbers to special values of 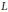 $L$ –functions.
$L$ –functions.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015
References
- 7
- Cited by

