Refine search
Actions for selected content:
13 results
COHOMOLOGY ISOMORPHISM OF SYMMETRIC POWER OF COTANGENT BUNDLE OF BALL QUOTIENT AND ITS TOROIDAL COMPACTIFICATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 11 December 2025, e1
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHERENCE OF MULTIPLIER SUBMODULE SHEAVES ON GENERIC COMPLEX TORI
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 666-673
- Print publication:
- December 2025
-
- Article
- Export citation
Invariant divisors and equivariant line bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSION OF COHOMOLOGY CLASSES FOR VECTOR BUNDLES WITH SINGULAR HERMITIAN METRICS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 259 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 562-580
- Print publication:
- September 2025
-
- Article
- Export citation
ON A BOGOMOLOV TYPE VANISHING THEOREM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 170-182
- Print publication:
- March 2025
-
- Article
- Export citation
DUAL NAKANO POSITIVITY AND SINGULAR NAKANO POSITIVITY OF DIRECT IMAGE SHEAVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 55-78
- Print publication:
- March 2025
-
- Article
- Export citation
Positivity of Schur forms for strongly decomposably positive vector bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 January 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONCAVITY PROPERTY OF MINIMAL
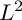 $L^{2}$ INTEGRALS WITH LEBESGUE MEASURABLE GAIN
$L^{2}$ INTEGRALS WITH LEBESGUE MEASURABLE GAIN
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 05 June 2023, pp. 842-905
- Print publication:
- December 2023
-
- Article
- Export citation
Positivity of direct images with a Poincaré type twist
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 October 2022, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SINGULAR HERMITIAN METRICS WITH ISOLATED SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 980-989
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic Zeta Functions and Equivariant Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 376-389
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
A Takayama-type extension theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 522-540
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Lp -curvature and the Cauchy-Riemann equation near an isolated singular point
-
- Journal:
- Nagoya Mathematical Journal / Volume 164 / December 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 35-51
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation











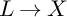

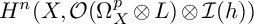
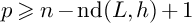


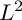
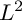
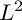
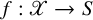
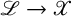
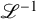

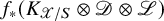
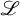
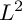
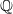 -divisor that has Kawamata log terminal singularities on the submanifold from which extension occurs. In this paper we weaken the positivity assumptions on the twisting line bundle to what we believe to be the minimal positivity hypotheses. The main new idea is an
-divisor that has Kawamata log terminal singularities on the submanifold from which extension occurs. In this paper we weaken the positivity assumptions on the twisting line bundle to what we believe to be the minimal positivity hypotheses. The main new idea is an 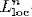 -curvature, to admit the Sobolev inequality and to have suitable volume growth near
-curvature, to admit the Sobolev inequality and to have suitable volume growth near 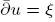 has a smooth solution on a punctured neighbourhood of
has a smooth solution on a punctured neighbourhood of 