Hostname: page-component-784d4fb959-g9298 Total loading time: 0 Render date: 2025-07-17T00:08:48.669Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A BOGOMOLOV TYPE VANISHING THEOREM

Part of: Holomorphic fiber spaces (Co)homology theory Compact analytic spaces

Published online by Cambridge University Press:  13 January 2025

ZHI LI Open the ORCID record for ZHI LI [Opens in a new window] ,
XIANKUI MENG Open the ORCID record for XIANKUI MENG [Opens in a new window] ,
JIAFU NING Open the ORCID record for JIAFU NING [Opens in a new window] ,
ZHIWEI WANG Open the ORCID record for ZHIWEI WANG [Opens in a new window]  and
XIANGYU ZHOU Open the ORCID record for XIANGYU ZHOU [Opens in a new window]
ZHI LI
Affiliation:
Department of Mathematics, School of Science Key Laboratory of Mathematics and Information Networks (Ministry of Education) Beijing University of Posts and Telecommunications Beijing 100876 China lizhi@amss.ac.cn, lizhi10@foxmail.com
XIANKUI MENG*
Affiliation:
Department of Mathematics, School of Science Key Laboratory of Mathematics and Information Networks (Ministry of Education) Beijing University of Posts and Telecommunications Beijing 100876 China
JIAFU NING*
Affiliation:
School of Mathematics and Statistics HNP-LAMA Central South University Changsha Hunan 410083 China
ZHIWEI WANG
Affiliation:
Laboratory of Mathematics and Complex Systems (Ministry of Education) School of Mathematical Sciences Beijing Normal University Beijing 100875 China zhiwei@bnu.edu.cn
XIANGYU ZHOU
Affiliation:
Institute of Mathematics Academy of Mathematics and Systems Sciences Hua Loo-Keng Key Laboratory of Mathematics Chinese Academy of Sciences Beijing 100190 China xyzhou@math.ac.cn
*
mengxiankui@amss.ac.cn
jfning@csu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be a compact Kähler manifold, and let 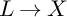$L \rightarrow X$ be a holomorphic line bundle equipped with a singular metric h such that the curvature $\mathrm {i}\Theta _{L,h}\geqslant 0$ in the sense of currents. The main result of this paper is the vanishing of 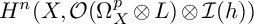$H^n(X,\mathcal {O}(\Omega ^p_X\otimes L)\otimes \mathcal {I}(h))$ for 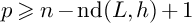$p\geqslant n-\operatorname {nd}(L,h)+1$, which generalizes Bogomolov’s vanishing theorem and Watanabe’s result.

Keywords

L2 estimatescohomology vanishingsingular Hermitian metricsnumerical dimension

MSC classification

Primary: 32L20: Vanishing theorems 32L10: Sheaves and cohomology of sections of holomorphic vector bundles, general results 32J25: Transcendental methods of algebraic geometry 14F17: Vanishing theorems 14F18: Multiplier ideals

Information

Type
Article
Information
Nagoya Mathematical Journal , Volume 257 , March 2025 , pp. 170 - 182
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bogomolov, F. A., Holomorphic tensors and vector bundles on projective varieties , Math. USSR, Izv. 13 (1979), 499–555.CrossRefGoogle Scholar
Bogomolov, F. A., Unstable vector bundles and curves on surfaces , Proc. Int. Congr. Math., Helsinki, 1978 2 (1980), 517–524.Google Scholar
Boucksom, S., Cônes positifs des variétés complexes compactes. PhD thesis, 2002 (in French).Google Scholar
Cao, J., Numerical dimension and a Kawamata-Viehweg-nadel-type vanishing theorem on compact Kähler manifolds , Compos. Math. 150 (2014), no. 11, 1869–1902.CrossRefGoogle Scholar
Demailly, J.-P., Estimations L2 pour l’opérateur $\bar{\partial}$ d’un fibre vectoriel holomorphe semi-positif au-dessus d’une variété Kaehlerienne complete , Ann. Sci. Éc. Norm. Supér. (4) 15 (1982), 457–511.CrossRefGoogle Scholar
Demailly, J.-P., Analytic Methods in Algebraic Geometry, Surveys of Modern Mathematics, Higher Education Press, Beijing, 2010.Google Scholar
Demailly, J.-P., Complex analytic and differential geometry, 2012. https://www-fourier.ujf-grenoble.fr/demailly/documents.html.Google Scholar
Demailly, J.-P., “ On the cohomology of pseudoeffective line bundles ”, in Complex Geometry and Dynamics. The Abel Symposium 2013, Trondheim, Norway, July 2–5, 2013, Springer, Cham, 2015, pp. 51–99.Google Scholar
Demailly, J.-P. and Peternell, T., A Kawamata–Viehweg vanishing theorem on compact Kähler manifolds , J. Differ. Geom. 63 (2003), no. 2, 231–277.CrossRefGoogle Scholar
Demailly, J.-P., Peternell, T. and Schneider, M., Pseudo-effective line bundles on compact Kähler manifolds , Int. J. Math. 12 (2001), no. 6, 689–741.CrossRefGoogle Scholar
Esnault, H. and Viehweg, E., Lectures on Vanishing Theorems. Notes, Grew Out of the DMV-Seminar on Algebraic Geometry, held at Reisensburg, October 13–19, 1991, DMV Semin., 20, Birkhäuser Verlag, Basel, 1992.Google Scholar
Graf, P., Bogomolov–Sommese vanishing on log canonical pairs , J. Reine Angew. Math. 702 (2015), 109–142.CrossRefGoogle Scholar
Guan, Q. and Zhou, X., A proof of Demailly’s strong openness conjecture , Ann. Math. 2 (2015), no. 182, 605–616.CrossRefGoogle Scholar
Mourougane, C., Versions kählériennes du théorème d’annulation de bogomolov , Collect. Math. 49 (1998), nos. 2–3, 433–445.Google Scholar
Shiffman, B. and Sommese, A. J., Vanishing Theorems on Complex Manifolds, Prog. Math., 56, Birkhäuser, Cham, 1985.CrossRefGoogle Scholar
Watanabe, Y., Bogomolov–Sommese type vanishing theorem for holomorphic vector bundles equipped with positive singular Hermitian metrics , Math. Z. 303 (2023), no. 4, 23, Id/No 92.CrossRefGoogle Scholar
Wu, X., On a vanishing theorem due to Bogomolov, Preprint, 2020, arXiv:2011.13751 [math.CV].Google Scholar