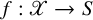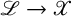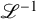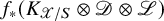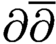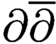Refine search
Actions for selected content:
11 results
Deformed Aeppli cohomology: canonical deformations and jumping formulas
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-34
-
- Article
- Export citation
DUAL NAKANO POSITIVITY AND SINGULAR NAKANO POSITIVITY OF DIRECT IMAGE SHEAVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 55-78
- Print publication:
- March 2025
-
- Article
- Export citation
Positivity of direct images with a Poincaré type twist
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 October 2022, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Group actions on local moduli space of holomorphic vector bundles
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 August 2022, pp. 553-567
- Print publication:
- June 2023
-
- Article
- Export citation
Smoothing toroidal crossing spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 August 2021, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POWER SERIES PROOFS FOR LOCAL STABILITIES OF KÄHLER AND BALANCED STRUCTURES WITH MILD
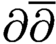 $\partial \overline {\partial }$-LEMMA
$\partial \overline {\partial }$-LEMMA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 08 June 2021, pp. 305-354
- Print publication:
- June 2022
-
- Article
- Export citation
The Kodaira Problem for Kähler Spaces with Vanishing First Chern Class
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 15 March 2021, e24
-
- Article
-
- You have access
- Open access
- Export citation
OBSTRUCTION THEORY FOR SUPERMANIFOLDS AND DEFORMATIONS OF SUPERCONFORMAL STRUCTURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 15 March 2017, pp. 512-514
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Global Geometrical Coordinates on Falbel's Cross-Ratio Variety
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 2 / 01 June 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 285-294
- Print publication:
- 01 June 2009
-
- Article
-
- You have access
- Export citation
JACOBI COHOMOLOGY, LOCAL GEOMETRY OF MODULI SPACES, AND HITCHIN CONNECTIONS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 92 / Issue 3 / May 2006
- Published online by Cambridge University Press:
- 18 April 2006, pp. 545-580
- Print publication:
- May 2006
-
- Article
- Export citation
DEFORMATION OF 2-STEP NILMANIFOLDS WITH ABELIAN COMPLEX STRUCTURES
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 22 February 2006, pp. 173-193
- Print publication:
- February 2006
-
- Article
- Export citation