In this paper we study the existence and the analytic dependence upon domain perturbation of the solutions of a nonlinear nonautonomous transmission problem for the Laplace equation. The problem is defined in a pair of sets consisting of a perforated domain and an inclusion whose shape is determined by a suitable diffeomorphism $\phi$. First we analyse the case in which the inclusion is a fixed domain. Then we will perturb the inclusion and study the arising boundary value problem and the dependence of a specific family of solutions upon the perturbation parameter $\phi$.

We consider a nonlinear Robin problem for the Poisson equation in an unbounded periodically perforated domain. The domain has a periodic structure, and the size of each cell is determined by a positive parameter δ. The relative size of each periodic perforation is determined by a positive parameter ε. Under suitable assumptions, such a problem admits a family of solutions which depends on ε and δ. We analyse the behaviour the energy integral of such a family as (ε, δ) tends to (0, 0) by an approach that represents an alternative to asymptotic expansions and classical homogenization theory.

Let $E$ and $D$ be open subsets of $\mathbb{R}^{n+1}$ such that $\overline{D}$ is a compact subset of $E$, and let $v$ be a supertemperature on $E$. We call a temperature $u$ on $D$extendable by$v$ if there is a supertemperature $w$ on $E$ such that $w=u$ on $D$ and $w=v$ on $E\backslash \overline{D}$. Such a temperature need not be a thermic minorant of $v$ on $D$. We show that either there is a unique temperature extendable by $v$, or there are infinitely many. Examples of temperatures extendable by $v$ include the greatest thermic minorant $GM_{v}^{D}$ of $v$ on $D$, and the Perron–Wiener–Brelot solution of the Dirichlet problem $S\!_{v}^{D}$ on $D$ with boundary values the restriction of $v$ to $\unicode[STIX]{x2202}D$. In the case where these two examples are distinct, we give a formula for producing infinitely many more. Clearly $GM_{v}^{D}$ is the greatest extendable thermic minorant, but we also prove that there is a least one, which is not necessarily equal to $S\!_{v}^{D}$.

We present a simple, accurate method for computing singular or nearly singular integrals on a smooth, closed surface, such as layer potentials for harmonic functions evaluated at points on or near the surface. The integral is computed with a regularized kernel and corrections are added for regularization and discretization, which are found from analysis near the singular point. The surface integrals are computed from a new quadrature rule using surface points which project onto grid points in coordinate planes. The method does not require coordinate charts on the surface or special treatment of the singularity other than the corrections. The accuracy is about O(h3), where h is the spacing in the background grid, uniformly with respect to the point of evaluation, on or near the surface. Improved accuracy is obtained for points on the surface. The treecode of Duan and Krasny for Ewald summation is used to perform sums. Numerical examples are presented with a variety of surfaces.

For a subfunction u, associated with the stationary Schrödinger operator, which is dominated on the boundary by a certain function on a cone, we generalise the classical Phragmén-Lindelöf theorem by making an a-harmonic majorant of u.

We discuss here the boundedness of the fractional integral operator Iα and its generalized version on generalized nonhomogeneous Morrey spaces. To prove the boundedness of Iα, we employ the boundedness of the so-called maximal fractional integral operator Ia,κ*. In addition, we prove an Olsen-type inequality, which is analogous to that in the case of homogeneous type.

Modifications of balayage spaces are studied which, in probabilistic terms, correspond to killing and transitions (creation of mass combined with jumps). This is achieved by a modification of harmonic kernels for sufficiently small open sets. Applications to coupling of elliptic and parabolic partial differential equations of second order are discussed.

By using integration by parts and Stokes' formula the authors give a new definition of the Hadamard principal value of higher order singular integrals on the complex hypersphere in Cn. Then the transformation formula for the higher order singular integrals is deduced.

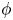
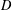
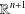
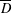
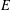
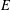
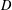
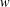
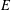
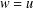
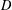
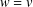
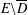
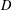
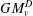
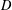
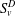
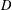
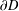
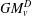
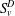
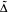Let be the invariant Laplacian on the open unit ball 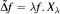B of Cn and let Xλ denote the set of those f € C2(B) such that counterparts of some known results on X0, i.e. on M-harmonic functions, are investigated here. We distinguish those complex numbers λ for which the real parts of functions in Xλ belongs to Xλ. We distinguish those λ for which the Maximum Modulus Priniple remains true. A kind of weighted Maximum Modulus Principle is presented. As an application, setting α ≥ ½ and λ = 4n2α(α — 1), we obtain a necessary and sufficient condition for a function f in Xλ to be represented as

for some F ∊ LP(∂B).

In this note we obtain a sharp estimate for a radial derivative of bounded harmonic functions in the ball.