Article contents
EXTENDABLE TEMPERATURES
Published online by Cambridge University Press: 27 February 2019
Abstract
Let 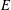 $E$ and
$E$ and 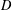 $D$ be open subsets of
$D$ be open subsets of 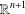 $\mathbb{R}^{n+1}$ such that
$\mathbb{R}^{n+1}$ such that 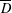 $\overline{D}$ is a compact subset of
$\overline{D}$ is a compact subset of 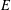 $E$, and let
$E$, and let  $v$ be a supertemperature on
$v$ be a supertemperature on 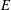 $E$. We call a temperature
$E$. We call a temperature  $u$ on
$u$ on 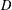 $D$extendable by
$D$extendable by $v$ if there is a supertemperature
$v$ if there is a supertemperature 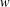 $w$ on
$w$ on 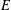 $E$ such that
$E$ such that 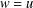 $w=u$ on
$w=u$ on 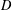 $D$ and
$D$ and 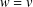 $w=v$ on
$w=v$ on 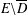 $E\backslash \overline{D}$. Such a temperature need not be a thermic minorant of
$E\backslash \overline{D}$. Such a temperature need not be a thermic minorant of  $v$ on
$v$ on 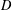 $D$. We show that either there is a unique temperature extendable by
$D$. We show that either there is a unique temperature extendable by  $v$, or there are infinitely many. Examples of temperatures extendable by
$v$, or there are infinitely many. Examples of temperatures extendable by  $v$ include the greatest thermic minorant
$v$ include the greatest thermic minorant 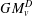 $GM_{v}^{D}$ of
$GM_{v}^{D}$ of  $v$ on
$v$ on 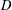 $D$, and the Perron–Wiener–Brelot solution of the Dirichlet problem
$D$, and the Perron–Wiener–Brelot solution of the Dirichlet problem 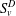 $S\!_{v}^{D}$ on
$S\!_{v}^{D}$ on 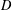 $D$ with boundary values the restriction of
$D$ with boundary values the restriction of  $v$ to
$v$ to 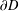 $\unicode[STIX]{x2202}D$. In the case where these two examples are distinct, we give a formula for producing infinitely many more. Clearly
$\unicode[STIX]{x2202}D$. In the case where these two examples are distinct, we give a formula for producing infinitely many more. Clearly 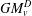 $GM_{v}^{D}$ is the greatest extendable thermic minorant, but we also prove that there is a least one, which is not necessarily equal to
$GM_{v}^{D}$ is the greatest extendable thermic minorant, but we also prove that there is a least one, which is not necessarily equal to 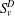 $S\!_{v}^{D}$.
$S\!_{v}^{D}$.
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 297 - 303
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by

