No CrossRef data available.
Article contents
Lp Behavior of the Eigenfunctions of the Invariant Laplacian
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 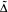 be the invariant Laplacian on the open unit ball B of Cn and let Xλ denote the set of those f € C2(B) such that
be the invariant Laplacian on the open unit ball B of Cn and let Xλ denote the set of those f € C2(B) such that 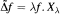 counterparts of some known results on X 0, i.e. on M-harmonic functions, are investigated here. We distinguish those complex numbers λ for which the real parts of functions in Xλ belongs to Xλ . We distinguish those λ for which the Maximum Modulus Priniple remains true. A kind of weighted Maximum Modulus Principle is presented. As an application, setting α ≥ ½ and λ = 4n 2 α(α — 1), we obtain a necessary and sufficient condition for a function f in Xλ to be represented as
counterparts of some known results on X 0, i.e. on M-harmonic functions, are investigated here. We distinguish those complex numbers λ for which the real parts of functions in Xλ belongs to Xλ . We distinguish those λ for which the Maximum Modulus Priniple remains true. A kind of weighted Maximum Modulus Principle is presented. As an application, setting α ≥ ½ and λ = 4n 2 α(α — 1), we obtain a necessary and sufficient condition for a function f in Xλ to be represented as
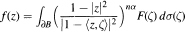
for some F ∊ LP (∂B).
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1993
References
[K]
Kwon, E. G., One radius theorem for the eigenfunctionsofthe invariant Laplacian, Proc. AMS. 116(1992), 27–34.Google Scholar
[KK] Kim, H. O. and Kwon, E. G., M-invariant subspaces of Xλ
, Illinois Math, J., to appear.Google Scholar
[R] Rudin, Walter, Function theory in the unit ball ofCn, Springer-Verlag, New York, 1980.Google Scholar
[SI Slater, Lucy John, Generalized hyper geometricfunctions, Cambridge University Press, 1966.Google Scholar

