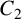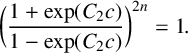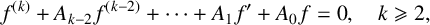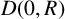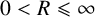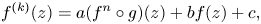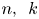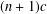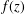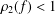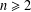Refine search
Actions for selected content:
45 results
AN ASYMPTOTIC ESTIMATE FOR THE CHARACTERISTIC AND NUMBER OF FIXED POINTS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 01 August 2025, pp. 648-665
- Print publication:
- December 2025
-
- Article
- Export citation
A study of transcendental entire solutions of several nonlinear partial differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 22 July 2025, pp. 1329-1369
-
- Article
- Export citation
On an open problem of value sharing and differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1110-1136
-
- Article
- Export citation
A note on Hayman’s problem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 18 December 2024, pp. 620-627
- Print publication:
- June 2025
-
- Article
- Export citation
Defect relation for holomorphic maps from complex discs into projective varieties and hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 157-172
-
- Article
- Export citation
NOTES ON FERMAT-TYPE DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 324-335
- Print publication:
- April 2025
-
- Article
- Export citation
A TROPICAL ANALOGUE OF THE LEMMA ON THE LOGARITHMIC DERIVATIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 20 May 2024, pp. 303-312
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE DIFFERENCE ANALOGUE OF THE TUMURA–HAYMAN–CLUNIE THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 145-154
- Print publication:
- August 2024
-
- Article
- Export citation
DESCRIPTION OF GROWTH AND OSCILLATION OF SOLUTIONS OF COMPLEX LDE’S
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 16 June 2022, pp. 145-171
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CARLSON–GRIFFITHS THEORY FOR COMPLETE KÄHLER MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 14 February 2022, pp. 2337-2365
- Print publication:
- September 2023
-
- Article
- Export citation
On meromorphic solutions of functional-differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 10 February 2022, pp. 263-278
-
- Article
- Export citation
On unavoidable families of meromorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 18 November 2021, pp. 114-123
- Print publication:
- March 2023
-
- Article
- Export citation
Dual exponential polynomials and a problem of Ozawa
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 16 June 2021, pp. 701-719
- Print publication:
- June 2022
-
- Article
- Export citation
On the number of linearly independent admissible solutions to linear differential and linear difference equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 30 July 2020, pp. 1556-1591
- Print publication:
- December 2021
-
- Article
- Export citation
Restrictions on meromorphic solutions of Fermat type equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 08 May 2020, pp. 654-665
-
- Article
- Export citation
ON THE PERIODICITY OF TRANSCENDENTAL ENTIRE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 453-465
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Entropy of transcendental entire functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 338-348
- Print publication:
- February 2021
-
- Article
- Export citation
GAUSSIAN CURVATURE AND UNICITY PROBLEM OF GAUSS MAPS OF VARIOUS CLASSES OF SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 18 March 2019, pp. 275-297
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
A Note on a Unicity Theorem for the Gauss Maps of Complete Minimal Surfaces in Euclidean Four-space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 292-300
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
Function-theoretic Properties for the Gauss Maps of Various Classes of Surfaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 6 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1411-1434
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation