Article contents
On the number of linearly independent admissible solutions to linear differential and linear difference equations
Published online by Cambridge University Press: 30 July 2020
Abstract
A classical theorem of Frei states that if 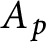 $A_p$ is the last transcendental function in the sequence
$A_p$ is the last transcendental function in the sequence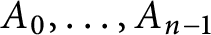 $A_0,\ldots ,A_{n-1}$ of entire functions, then each solution base of the differential equation
$A_0,\ldots ,A_{n-1}$ of entire functions, then each solution base of the differential equation 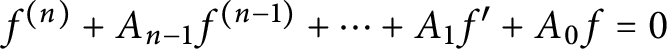 $f^{(n)}+A_{n-1}f^{(n-1)}+\cdots +A_{1}f'+A_{0}f=0$ contains at least
$f^{(n)}+A_{n-1}f^{(n-1)}+\cdots +A_{1}f'+A_{0}f=0$ contains at least 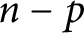 $n-p$ entire functions of infinite order. Here, the transcendental coefficient
$n-p$ entire functions of infinite order. Here, the transcendental coefficient 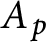 $A_p$ dominates the growth of the polynomial coefficients
$A_p$ dominates the growth of the polynomial coefficients  $A_{p+1},\ldots ,A_{n-1}$. By expressing the dominance of
$A_{p+1},\ldots ,A_{n-1}$. By expressing the dominance of 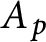 $A_p$ in different ways and allowing the coefficients
$A_p$ in different ways and allowing the coefficients  $A_{p+1},\ldots ,A_{n-1}$ to be transcendental, we show that the conclusion of Frei’s theorem still holds along with an additional estimation on the asymptotic lower bound for the growth of solutions. At times, these new refined results give a larger number of linearly independent solutions of infinite order than the original theorem of Frei. For such solutions, we show that
$A_{p+1},\ldots ,A_{n-1}$ to be transcendental, we show that the conclusion of Frei’s theorem still holds along with an additional estimation on the asymptotic lower bound for the growth of solutions. At times, these new refined results give a larger number of linearly independent solutions of infinite order than the original theorem of Frei. For such solutions, we show that 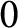 $0$ is the only possible finite deficient value. Previously, this property has been known to hold for so-called admissible solutions and is commonly cited as Wittich’s theorem. Analogous results are discussed for linear differential equations in the unit disc, as well as for complex difference and complex q-difference equations.
$0$ is the only possible finite deficient value. Previously, this property has been known to hold for so-called admissible solutions and is commonly cited as Wittich’s theorem. Analogous results are discussed for linear differential equations in the unit disc, as well as for complex difference and complex q-difference equations.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
References
- 2
- Cited by


