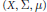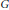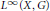Refine search
Actions for selected content:
11 results
Integral equivariant cohomology of affine Grassmannians
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 727-741
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRUNCATED AFFINE SPRINGER FIBERS AND ARTHUR’S WEIGHTED ORBITAL INTEGRALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1757-1818
- Print publication:
- July 2023
-
- Article
- Export citation
A construction of complex analytic elliptic cohomology from double free loop spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 26 July 2021, pp. 1853-1897
- Print publication:
- August 2021
-
- Article
- Export citation
PROJECTIVE LOOPS GENERATE RATIONAL LOOP GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 17 August 2020, pp. 459-485
- Print publication:
- March 2022
-
- Article
- Export citation
GEOMETRY OF KOTTWITZ–VIEHMANN VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 November 2019, pp. 1-65
- Print publication:
- January 2022
-
- Article
- Export citation
Completeness of Infinite-dimensional Lie Groups in Their Left Uniformity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 131-152
- Print publication:
- February 2019
-
- Article
-
- You have access
- Open access
- Export citation
Generalized affine Springer fibres
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 03 January 2012, pp. 569-609
- Print publication:
- July 2012
-
- Article
- Export citation
Unitarization of Loop Group Representations of Fundamental Groups
-
- Journal:
- Nagoya Mathematical Journal / Volume 187 / September 2007
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-33
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
A Steinberg Cross Section for Non-Connected Affine Kac—Moody Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 3 / 01 June 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 625-642
- Print publication:
- 01 June 2006
-
- Article
-
- You have access
- Export citation
Some Examples of Hecke Algebras for Two-Dimensional Local Fields
-
- Journal:
- Nagoya Mathematical Journal / Volume 183 / 2006
- Published online by Cambridge University Press:
- 11 January 2016, pp. 57-84
- Print publication:
- 2006
-
- Article
-
- You have access
- Export citation
Lie Groups of Measurable Mappings
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 5 / 01 October 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 969-999
- Print publication:
- 01 October 2003
-
- Article
-
- You have access
- Export citation
 .
.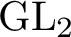
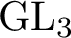
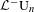
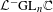
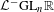
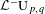
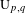
 and determine all possible ways of the unitarization. Such matrix functions can be regarded as images of the generators for the fundamental group of a surface in an
and determine all possible ways of the unitarization. Such matrix functions can be regarded as images of the generators for the fundamental group of a surface in an