Article contents
PROJECTIVE LOOPS GENERATE RATIONAL LOOP GROUPS
Published online by Cambridge University Press: 17 August 2020
Abstract
We generalize Uhlenbeck’s generator theorem of 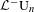 ${\mathcal{L}}^{-}\operatorname{U}_{n}$ to the full rational loop group
${\mathcal{L}}^{-}\operatorname{U}_{n}$ to the full rational loop group 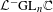 ${\mathcal{L}}^{-}\operatorname{GL}_{n}\mathbb{C}$ and its subgroups
${\mathcal{L}}^{-}\operatorname{GL}_{n}\mathbb{C}$ and its subgroups 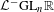 ${\mathcal{L}}^{-}\operatorname{GL}_{n}\mathbb{R}$,
${\mathcal{L}}^{-}\operatorname{GL}_{n}\mathbb{R}$, 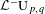 ${\mathcal{L}}^{-}\operatorname{U}_{p,q}$: they are all generated by just simple projective loops. Recall that Terng–Uhlenbeck studied the dressing actions of such projective loops as generalized Bäcklund transformations for integrable systems. Our result makes a nice supplement: any rational dressing is the composition of these Bäcklund transformations. This conclusion is surprising in the sense that Lie theory suggests the indispensable role of nilpotent loops in the case of noncompact reality conditions, and nilpotent dressings appear quite complicated and mysterious. The sacrifice is to introduce some extra fake singularities. So we also propose a set of generators if fake singularities are forbidden. A very geometric and physical construction of
${\mathcal{L}}^{-}\operatorname{U}_{p,q}$: they are all generated by just simple projective loops. Recall that Terng–Uhlenbeck studied the dressing actions of such projective loops as generalized Bäcklund transformations for integrable systems. Our result makes a nice supplement: any rational dressing is the composition of these Bäcklund transformations. This conclusion is surprising in the sense that Lie theory suggests the indispensable role of nilpotent loops in the case of noncompact reality conditions, and nilpotent dressings appear quite complicated and mysterious. The sacrifice is to introduce some extra fake singularities. So we also propose a set of generators if fake singularities are forbidden. A very geometric and physical construction of 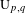 $\operatorname{U}_{p,q}$ is obtained as a by-product, generalizing the classical construction of unitary groups.
$\operatorname{U}_{p,q}$ is obtained as a by-product, generalizing the classical construction of unitary groups.
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 2 , March 2022 , pp. 459 - 485
- Copyright
- © Cambridge University Press 2020
References
- 2
- Cited by


