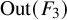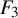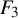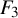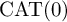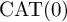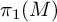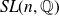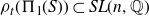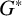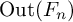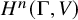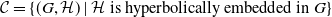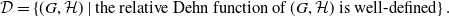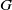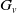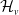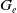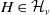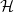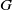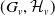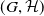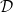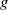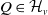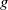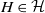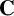Refine search
Actions for selected content:
65 results
A note on morphisms to wreath products
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-28
-
- Article
- Export citation
Rigidity phenomena and the statistical properties of group actions on
 $\text {CAT}(0)$ cube complexes
$\text {CAT}(0)$ cube complexes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 September 2025, e150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random walks and contracting elements I: deviation inequality and limit laws
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 1512-1575
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The conjugacy problem for
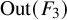 $\operatorname {Out}(F_3)$
$\operatorname {Out}(F_3)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic Metric Spaces and Stochastic Embeddings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of virtually free groups among hyperbolic groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 477-483
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROPER
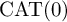 $\mathrm {CAT(0)}$ ACTIONS OF UNIPOTENT-FREE LINEAR GROUPS
$\mathrm {CAT(0)}$ ACTIONS OF UNIPOTENT-FREE LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 587-601
- Print publication:
- March 2025
-
- Article
- Export citation
Finitely generated simple sharply 2-transitive groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 1941-1957
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic one-relator groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CORRECTION TO ‘AUTOMORPHISM AND OUTER AUTOMORPHISM GROUPS OF RIGHT-ANGLED ARTIN GROUPS ARE NOT RELATIVELY HYPERBOLIC’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 30 April 2024, pp. 171-176
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zariski dense surface subgroups in
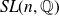 $SL(n,\mathbb{Q})$ with odd
$SL(n,\mathbb{Q})$ with odd  $n$
$n$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 26 March 2024, pp. 643-653
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Examples of hyperbolic spaces without the properties of quasi-ball or bounded eccentricity
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. 440-448
- Print publication:
- May 2024
-
- Article
- Export citation
COMPLETE EMBEDDINGS OF GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 136-144
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classifying spaces for families of abelian subgroups of braid groups, RAAGs and graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 290-307
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR GROWTH OF TRANSLATION LENGTHS OF RANDOM ISOMETRIES ON GROMOV HYPERBOLIC SPACES AND TEICHMÜLLER SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1751-1795
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability for hyperbolic groups acting on boundary spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 September 2023, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cusps, Kleinian groups, and Eisenstein series
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 August 2023, e75
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative Dehn functions, hyperbolically embedded subgroups and combination theorems
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 25 August 2023, pp. 1-23
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relatively hyperbolic groups with strongly shortcut parabolics are strongly shortcut
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 17 April 2023, pp. 367-380
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLICATION TABLES AND WORD-HYPERBOLICITY IN FREE PRODUCTS OF SEMIGROUPS, MONOIDS AND GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 17 March 2023, pp. 396-430
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation