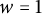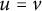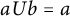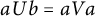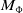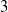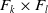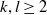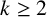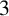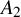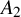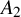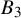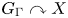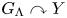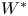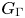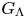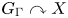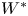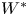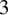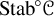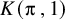Refine search
Actions for selected content:
54 results
Higher incoherence of the automorphism groups of a free group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stratified braid groups: monodromy
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 259-292
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Right-angled Artin groups and the cohomology basis graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 634-654
-
- Article
- Export citation
Membership problems for positive one-relator groups and one-relation monoids
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Centers of Artin groups defined on cones
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 44-50
-
- Article
- Export citation
CONGRUENCE SUBGROUPS OF BRAID GROUPS AND CRYSTALLOGRAPHIC QUOTIENTS. PART I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 145-163
- Print publication:
- April 2025
-
- Article
- Export citation
Corrigendum: A certain structure of Artin groups and the isomorphism conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 729-730
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Dehn functions of mapping tori of right-angled Artin groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 252-289
- Print publication:
- May 2024
-
- Article
- Export citation
The spherical growth series of Dyer groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 December 2023, pp. 168-187
-
- Article
- Export citation
FAITHFULNESS OF THE 2-BRAID GROUP VIA ZIGZAG ALGEBRA IN TYPE B
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 67-84
- Print publication:
- August 2024
-
- Article
- Export citation
TORIC REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 171-199
- Print publication:
- April 2024
-
- Article
- Export citation
A note on virtual duality and automorphism groups of right-angled Artin groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 573-581
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
q-deformed rational numbers and the 2-Calabi–Yau category of type
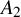 $A_{2}$
$A_{2}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 June 2023, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orbit equivalence rigidity of irreducible actions of right-angled Artin groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 860-887
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite image homomorphisms of the braid group and its generalizations
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 March 2023, pp. 430-445
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subsymmetric exchanged braids and the Burau matrix
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 154-187
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersection of parabolic subgroups in even Artin groups of FC-type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 18 October 2022, pp. 938-957
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parabolic subgroups of large-type Artin groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 393-414
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability conditions for contraction algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bouquets of curves in surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 90-97
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation