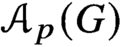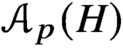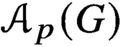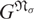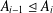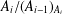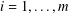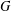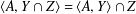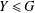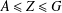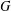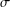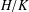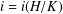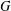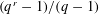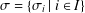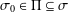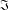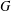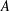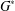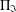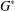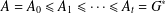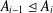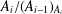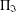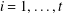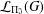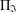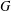Refine search
Actions for selected content:
16 results
A CHARACTERISATION OF SOLUBLE
 ${PST}$-GROUPS
${PST}$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 520-527
- Print publication:
- December 2024
-
- Article
- Export citation
FINITE GROUPS WITH LARGE CHERMAK–DELGADO LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 451-455
- Print publication:
- June 2023
-
- Article
- Export citation
Groups whose Chermak–Delgado lattice is a subgroup lattice of an abelian group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 June 2022, pp. 443-449
- Print publication:
- June 2023
-
- Article
- Export citation
An approach to Quillen’s conjecture via centralisers of simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e48
-
- Article
-
- You have access
- Open access
- Export citation
FINITE GROUPS WITH THE SAME JOIN GRAPH AS A FINITE NILPOTENT GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 17 August 2020, pp. 640-650
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
ON THE σ-NILPOTENT NORM AND THE σ-NILPOTENT LENGTH OF A FINITE GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 27 February 2020, pp. 121-132
- Print publication:
- January 2021
-
- Article
- Export citation
A GENERALISATION OF FINITE PT-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 March 2018, pp. 396-405
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
GENERATION OF SECOND MAXIMAL SUBGROUPS AND THE EXISTENCE OF SPECIAL PRIMES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 07 November 2017, e25
-
- Article
-
- You have access
- Open access
- Export citation
ON THE LATTICE OF
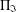 $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$ -SUBNORMAL SUBGROUPS OF A FINITE GROUP
$\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$ -SUBNORMAL SUBGROUPS OF A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 233-244
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
On Finite Groups with Dismantlable Subgroup Lattices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 1 / 01 March 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 182-187
- Print publication:
- 01 March 2015
-
- Article
-
- You have access
- Export citation
Fixed-point free action of an abelian group of odd non-squarefree exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 77-89
-
- Article
-
- You have access
- Export citation
OVERGROUPS OF PRIMITIVE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 01 August 2009, pp. 37-82
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
COEFFICIENTS OF THE PROBABILISTIC FUNCTION OF A MONOLITHIC GROUP*
-
- Journal:
- Glasgow Mathematical Journal / Volume 50 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 75-81
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
ON THE REDUCED LEFSCHETZ MODULE AND THE CENTRIC p-RADICAL SUBGROUPS II
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 22 February 2006, pp. 126-140
- Print publication:
- February 2006
-
- Article
- Export citation
Some new permutability properties of hypercentrally embedded subgroups of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-255
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation
On c-normality of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-304
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation