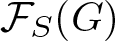 $\mathcal{F}_{S}(G)$
$\mathcal{F}_{S}(G)$
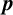 $\boldsymbol {p}$-GROUPS
$\boldsymbol {p}$-GROUPS
 ${PST}$-GROUPS
${PST}$-GROUPS
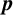 $\boldsymbol {p}$
-GROUPS
$\boldsymbol {p}$
-GROUPS
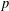 $p$-GROUPS
$p$-GROUPS