Hostname: page-component-7dd5485656-hw7sx Total loading time: 0 Render date: 2025-10-30T13:22:29.984Z Has data issue: false hasContentIssue false
  • English
  • Français

RATIONAL REPRESENTATIONS AND RATIONAL GROUP ALGEBRA OF VZ $\boldsymbol {p}$-GROUPS

Part of: Rings and algebras arising under various constructions Representation theory of groups

Published online by Cambridge University Press:  06 November 2024

RAM KARAN CHOUDHARY  and
SUNIL KUMAR PRAJAPATI
RAM KARAN CHOUDHARY
Affiliation:
Indian Institute of Technology, Bhubaneswar, Arugul Campus, Jatni, Khurda 752050, India e-mail: ramkchoudhary1997@gmail.com
SUNIL KUMAR PRAJAPATI*
Affiliation:
Indian Institute of Technology, Bhubaneswar, Arugul Campus, Jatni, Khurda 752050, India
*
e-mail: skprajapati@iitbbs.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we study rational matrix representations of VZ p-groups (p is any prime). Using our findings on VZ p-groups, we explicitly obtain all inequivalent irreducible rational matrix representations of all p-groups of order $\leq p^4$. Furthermore, we establish combinatorial formulae to determine the Wedderburn decompositions of rational group algebras for VZ p-groups and all p-groups of order 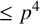$\leq p^4$, ensuring simplicity in the process.

Keywords

rational representationsWedderburn decompositionVZ-groupsp-groups

MSC classification

Primary: 20D15: Nilpotent groups, $p$-groups
Secondary: 20C15: Ordinary representations and characters 16S34: Group rings , Laurent polynomial rings

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 118 , Issue 1 , February 2025 , pp. 1 - 30
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author acknowledges University Grants Commission, Government of India. The corresponding author acknowledges SERB, Government of India for financial support through grant (MTR/2019/000118).

Communicated by Benjamin Martin

References

Ayoub, R. G. and Ayoub, C., ‘On the group ring of a finite abelian group’, Bull. Aust. Math. Soc. 1 (1969), 245–261.CrossRefGoogle Scholar
Bakshi, G. K. and Kaur, G., ‘Character triples and Shoda pairs’, J. Algebra 491 (2017), 447–473.CrossRefGoogle Scholar
Bakshi, G. K. and Kaur, G., ‘A generalization of strongly monomial groups’, J. Algebra 520 (2019), 419–439.CrossRefGoogle Scholar
Bakshi, G. K. and Maheshwary, S., ‘The rational group algebra of a normally monomial group’, J. Pure Appl. Algebra 218(9) (2014), 1583–1593.CrossRefGoogle Scholar
Bakshi, G. K. and Passi, I. B. S., ‘Primitive central idempotents in rational group algebras’, Comm. Algebra 40(4) (2012), 1413–1426.CrossRefGoogle Scholar
Burnside, W., Theory of Groups of Finite Order (Cambridge University Press, Cambridge, 1911).Google Scholar
del Río, Á. and Ruiz, M., ‘Computing large direct products of free groups in integral group rings’, Comm. Algebra 30(4) (2002), 1751–1767.CrossRefGoogle Scholar
Fernández-Alcober, G. A. and Moretó, A., ‘Groups with two extreme character degrees and their normal subgroups’, Trans. Amer. Math. Soc. 353(6) (2001), 2171–2192.CrossRefGoogle Scholar
Ford, C. E., ‘Characters of $p$ -groups’, Proc. Amer. Math. Soc. 101(4) (1987), 595–601.Google Scholar
Hall, P., ‘The classification of prime-power groups’, J. reine angew. Math. 182 (1940), 130–141.CrossRefGoogle Scholar
Herman, A., ‘On the automorphism group of rational group algebras of metacyclic groups’, Comm. Algebra 25(7) (1997), 2085–2097.CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (Dover Publications Inc., New York, 1994).Google Scholar
James, R., ‘The groups of order ${p}^6$ ( $p$ an odd prime)’, Math. Comp. 34(150) (1980), 613–637.Google Scholar
Jespers, E. and del Río, Á., ‘A structure theorem for the unit group of the integral group ring of some finite groups’, J. reine angew. Math. 521 (2000), 99–117.Google Scholar
Jespers, E. and del Río, Á., Group Ring Groups, Volume 1: Orders and Generic Constructions of Units (De Gruyter, Berlin, 2016).Google Scholar
Jespers, E. and Leal, G., ‘Generators of large subgroups of the unit group of integral group rings’, Manuscripta Math. 78(3) (1993), 303–315.CrossRefGoogle Scholar
Jespers, E., Leal, G. and Paques, A., ‘Central idempotents in rational group algebras of finite nilpotent groups’, J. Algebra Appl. 2(1) (2003), 57–62.CrossRefGoogle Scholar
Lewis, M. L., ‘Generalizing Camina groups and their character tables’, J. Group Theory 12(2) (2009), 209–218.CrossRefGoogle Scholar
Lewis, M. L., ‘The vanishing-off subgroup’, J. Algebra 321(4) (2009), 1313–1325.CrossRefGoogle Scholar
Newman, M. F., O’Brien, E. A. and Vaughan-Lee, M. R., ‘Presentations for the groups of order ${p}^6$ for prime $p\ge 7$ ’, Preprint, 2023, arXiv:2302.02677 [math.GR].Google Scholar
Olivieri, A., del Río, Á. and Simón, J. J., ‘On monomial characters and central idempotents of rational group algebras’, Comm. Algebra 32(4) (2004), 1531–1550.CrossRefGoogle Scholar
Olivieri, A., del Río, Á. and Simón, J. J., ‘The group of automorphisms of a rational group algebra of a finite metacyclic group’, Comm. Algebra 34(10) (2006), 3543–3567.CrossRefGoogle Scholar
Olteanu, G., ‘Computing the Wedderburn decomposition of group algebras by the Brauer–Witt theorem’, Math. Comp. 76(258) (2007), 1073–1087.CrossRefGoogle Scholar
Perlis, S. and Walker, G. L., ‘Abelian group algebras of finite order’, Trans. Amer. Math. Soc. 68(3) (1950), 420–426.CrossRefGoogle Scholar
Prajapati, S. K., Darafsheh, M. R. and Ghorbani, M., ‘Irreducible characters of $p$ -group of order $\le {p}^5$ ’, Algebr. Represent. Theory 20(5) (2017), 1289–1303.CrossRefGoogle Scholar
Prajapati, S. K. and Sharma, R., ‘Total character of a group $G$ with ( $G$ , $Z(G)$ ) as a generalized Camina pair’, Canad. Math. Bull. 59(2) (2016), 392–402.CrossRefGoogle Scholar
Reiner, I., ‘The Schur index in the theory of group representations’, Michigan Math. J. 8 (1961), 39–47.CrossRefGoogle Scholar
Ritter, J. and Sehgal, S. K., ‘Construction of units in integral group rings of finite nilpotent groups’, Trans. Amer. Math. Soc. 324(2) (1991), 603–621.CrossRefGoogle Scholar
Tappe, J., ‘On Isoclinic groups’, Math. Z. 148 (1976), 147–153.CrossRefGoogle Scholar
Yamada, T., The Schur Subgroup of the Brauer Group, Lecture Notes in Mathematics, 397 (Springer Verlag, Berlin, 1974).CrossRefGoogle Scholar
Yamada, T., ‘Types of faithful metacyclic $2$ -groups’, SUT J. Math. 28(1) (1992), 23–46.Google Scholar
Yamada, T., ‘Remarks on rational representations of a finite group’, SUT J. Math. 29(1) (1993), 71–77.Google Scholar