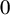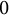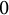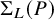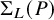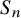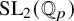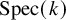Refine search
Actions for selected content:
77 results
Borel-type presentation of the torus-equivariant quantum K-ring of flag manifolds of type C
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 December 2025, e198
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The geometric Satake equivalence for integral motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 17 December 2025, pp. 2755-2851
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DENOMINATORS IN LUSZTIG’S ASYMPTOTIC HECKE ALGEBRA VIA THE PLANCHEREL FORMULA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived equivalences for trigonometric double affine Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Diagrammatics for the smallest quantum coideal and Jones–Wenzl projectors
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 April 2025, pp. 1-20
-
- Article
- Export citation
Quasi-polynomial representations of double affine Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 April 2025, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A categorical action of the shifted
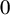 $0$-affine algebra
$0$-affine algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 April 2025, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalised Temperley–Lieb algebras of type G(r, p, n)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 April 2025, pp. 193-227
- Print publication:
- March 2025
-
- Article
- Export citation
Geometrization of the Satake transform for mod p Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 February 2025, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Oriented Temperley–Lieb algebras and combinatorial Kazhdan–Lusztig theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 January 2025, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
0-Hecke modules, domino tableaux, and type-B quasisymmetric functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regular Schur labeled skew shape posets and their 0-Hecke modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 November 2024, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantum wreath products and Schur–Weyl duality I
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An update on Haiman’s conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability in the category of smooth mod-p representations of
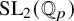 ${\mathrm {SL}}_2(\mathbb {Q}_p)$
${\mathrm {SL}}_2(\mathbb {Q}_p)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-15
- Print publication:
- January 2025
-
- Article
- Export citation
Affine Bruhat order and Demazure products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 April 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL CATEGORIES AND PRO-p IWAHORI–HECKE MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 04 April 2023, pp. 1029-1076
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subsymmetric exchanged braids and the Burau matrix
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 154-187
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double coset Markov chains
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 January 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation