1 Introduction
The 0-Hecke algebra
![]() $H_W(0)$
of a Coxeter system
$H_W(0)$
of a Coxeter system
![]() $(W,S)$
is the
$(W,S)$
is the
![]() $q=0$
specialization of the Hecke algebra
$q=0$
specialization of the Hecke algebra
![]() $H_W(q)$
of W. In type A, representations of
$H_W(q)$
of W. In type A, representations of
![]() $0$
-Hecke algebras can be interpreted in terms of the Hopf algebra
$0$
-Hecke algebras can be interpreted in terms of the Hopf algebra
![]() $\mathrm {QSym}$
of quasisymmetric functions; specifically, the quasisymmetric characteristic map [Reference Duchamp, Krob, Leclerc and Thibon8] defines an isomorphism between the Grothendieck group of finite-dimensional
$\mathrm {QSym}$
of quasisymmetric functions; specifically, the quasisymmetric characteristic map [Reference Duchamp, Krob, Leclerc and Thibon8] defines an isomorphism between the Grothendieck group of finite-dimensional
![]() $0$
-Hecke modules and
$0$
-Hecke modules and
![]() $\mathrm {QSym}$
. Much recent work, including [Reference Bardwell and Searles1, Reference Berg, Bergeron, Saliola, Serrano and Zabrocki2, Reference Niese, Sundaram, van Willigenburg, Vega and Wang12, Reference Searles16, Reference Tewari and van Willigenburg19], has been devoted to giving representation–theoretic interpretations of important bases of quasisymmetric functions by constructing families of type-A 0-Hecke modules that are associated with these bases via the quasisymmetric characteristic map.
$\mathrm {QSym}$
. Much recent work, including [Reference Bardwell and Searles1, Reference Berg, Bergeron, Saliola, Serrano and Zabrocki2, Reference Niese, Sundaram, van Willigenburg, Vega and Wang12, Reference Searles16, Reference Tewari and van Willigenburg19], has been devoted to giving representation–theoretic interpretations of important bases of quasisymmetric functions by constructing families of type-A 0-Hecke modules that are associated with these bases via the quasisymmetric characteristic map.
Recently, a uniform method for constructing type-A
![]() $0$
-Hecke modules was introduced in [Reference Searles17], based on an ascent-compatibility condition defined on subsets of symmetric groups. As far as we are aware, all of the
$0$
-Hecke modules was introduced in [Reference Searles17], based on an ascent-compatibility condition defined on subsets of symmetric groups. As far as we are aware, all of the
![]() $0$
-Hecke modules that have been constructed for notable families of quasisymmetric functions can be obtained via this ascent-compatibility framework. Our first main result, which we present in Section 3, consists of a type-independent definition of ascent-compatibility for all (not necessarily finite) Coxeter groups together with a consequent extension of the construction method for
$0$
-Hecke modules that have been constructed for notable families of quasisymmetric functions can be obtained via this ascent-compatibility framework. Our first main result, which we present in Section 3, consists of a type-independent definition of ascent-compatibility for all (not necessarily finite) Coxeter groups together with a consequent extension of the construction method for
![]() $0$
-Hecke modules from [Reference Searles16] from type A to all Coxeter groups. We show that any convex subset of the left weak order that has a unique maximal element is ascent-compatible, allowing the construction of large families of
$0$
-Hecke modules from [Reference Searles16] from type A to all Coxeter groups. We show that any convex subset of the left weak order that has a unique maximal element is ascent-compatible, allowing the construction of large families of
![]() $0$
-Hecke modules for any Coxeter system.
$0$
-Hecke modules for any Coxeter system.
We then specialize our attention to the type B case. There is a type-B analog of the type-A connection between
![]() $0$
-Hecke algebras and quasisymmetric functions: Chow [Reference Chow7] introduced the ring
$0$
-Hecke algebras and quasisymmetric functions: Chow [Reference Chow7] introduced the ring
![]() $\mathrm {QSym}^B$
of type-B quasisymmetric functions, and Huang [Reference Huang9] defined a quasisymmetric characteristic map from the Grothendieck group of finite-dimensional type-B 0-Hecke modules to
$\mathrm {QSym}^B$
of type-B quasisymmetric functions, and Huang [Reference Huang9] defined a quasisymmetric characteristic map from the Grothendieck group of finite-dimensional type-B 0-Hecke modules to
![]() $\mathrm {QSym}^B$
. Consequently, ascent-compatible subsets of hyperoctahedral groups give rise to families of type-B quasisymmetric functions that have representation – theoretic significance. As an application of our methods, we construct type-B 0-Hecke modules corresponding to families of type-B quasisymmetric functions defined by Mayorova and Vassilieva [Reference Mayorova and Vassilieva11] that exhibit a type-B analogue of Schur positivity.
$\mathrm {QSym}^B$
. Consequently, ascent-compatible subsets of hyperoctahedral groups give rise to families of type-B quasisymmetric functions that have representation – theoretic significance. As an application of our methods, we construct type-B 0-Hecke modules corresponding to families of type-B quasisymmetric functions defined by Mayorova and Vassilieva [Reference Mayorova and Vassilieva11] that exhibit a type-B analogue of Schur positivity.
In Section 4, we first consider the domino functions introduced by Mayorova and Vassilieva [Reference Mayorova and Vassilieva11]. These type-B analogs of Schur functions are defined in terms of domino tableaux of partition shape. We give a representation–theoretic interpretation of these functions by defining an action of the type-B
![]() $0$
-Hecke algebra on standard domino tableaux of a given shape: the quasisymmetric characteristics of the resulting type-B
$0$
-Hecke algebra on standard domino tableaux of a given shape: the quasisymmetric characteristics of the resulting type-B
![]() $0$
-Hecke modules are precisely the type-B Schur functions. We then consider the semistandard domino tableaux of shifted partition shape introduced by Chemli [Reference Chemli6] and used to provide an expansion formula for products of Schur Q-functions. We define a variant of these semistandard domino tableaux whose generating functions are in
$0$
-Hecke modules are precisely the type-B Schur functions. We then consider the semistandard domino tableaux of shifted partition shape introduced by Chemli [Reference Chemli6] and used to provide an expansion formula for products of Schur Q-functions. We define a variant of these semistandard domino tableaux whose generating functions are in
![]() $\mathrm {QSym}^B$
. These functions, which we call shifted domino functions, form type-B analogs of Schur Q-functions. We prove that shifted domino functions expand positively in the type-B peak functions introduced by Petersen [Reference Petersen15]. Our expansion is indexed by type-B peak sets of standard shifted domino tableaux, analogously to how peak sets of standard shifted tableaux index the expansion of Schur Q-functions in (type-A) peak functions.
$\mathrm {QSym}^B$
. These functions, which we call shifted domino functions, form type-B analogs of Schur Q-functions. We prove that shifted domino functions expand positively in the type-B peak functions introduced by Petersen [Reference Petersen15]. Our expansion is indexed by type-B peak sets of standard shifted domino tableaux, analogously to how peak sets of standard shifted tableaux index the expansion of Schur Q-functions in (type-A) peak functions.
In type A, the
![]() $0$
-Hecke–Clifford algebras are obtained by combining the
$0$
-Hecke–Clifford algebras are obtained by combining the
![]() $0$
-Hecke algebras and the Clifford algebras. Bergeron, Hivert, and Thibon defined a quasisymmetric characteristic map [Reference Bergeron, Hivert and Thibon3] from the Grothendieck group of finite-dimensional
$0$
-Hecke algebras and the Clifford algebras. Bergeron, Hivert, and Thibon defined a quasisymmetric characteristic map [Reference Bergeron, Hivert and Thibon3] from the Grothendieck group of finite-dimensional
![]() $0$
-Hecke–Clifford modules to the type-A peak algebra of Stembridge [Reference Stembridge18]. Type-A ascent-compatibility was applied in [Reference Searles17] to construct
$0$
-Hecke–Clifford modules to the type-A peak algebra of Stembridge [Reference Stembridge18]. Type-A ascent-compatibility was applied in [Reference Searles17] to construct
![]() $0$
-Hecke–Clifford modules whose quasisymmetric characteristics are certain bases of the peak algebra. In Section 5, we introduce a type-B analog of the
$0$
-Hecke–Clifford modules whose quasisymmetric characteristics are certain bases of the peak algebra. In Section 5, we introduce a type-B analog of the
![]() $0$
-Hecke–Clifford algebras and show that the isomorphism classes of the modules of these algebras induced from the simple type-B
$0$
-Hecke–Clifford algebras and show that the isomorphism classes of the modules of these algebras induced from the simple type-B
![]() $0$
-Hecke modules are indexed by the type-B peak sets. Moreover, we show that the quasisymmetric characteristics of the restrictions of these modules to the type-B
$0$
-Hecke modules are indexed by the type-B peak sets. Moreover, we show that the quasisymmetric characteristics of the restrictions of these modules to the type-B
![]() $0$
-Hecke algebra are precisely the type-B peak functions of Petersen [Reference Petersen15], thereby giving representation–theoretic significance to these functions.
$0$
-Hecke algebra are precisely the type-B peak functions of Petersen [Reference Petersen15], thereby giving representation–theoretic significance to these functions.
In Section 6, we prove a general result that allows us to compute the type-B quasisymmetric characteristic of the restriction of an induction of a type-B
![]() $0$
-Hecke module. This result applies whenever the module is obtained via the type-B ascent compatibility framework. We also apply it in order to give representation–theoretic significance to our aforementioned shifted domino functions.
$0$
-Hecke module. This result applies whenever the module is obtained via the type-B ascent compatibility framework. We also apply it in order to give representation–theoretic significance to our aforementioned shifted domino functions.
2 Preliminaries
2.1 Quasisymmetric functions
We use the notation
![]() $[n]=\{1,\ldots ,n\}$
and
$[n]=\{1,\ldots ,n\}$
and
![]() $[0,n]=\{0,1,\ldots ,n\}$
. A
$[0,n]=\{0,1,\ldots ,n\}$
. A ![]() is a finite tuple of positive integers. If
is a finite tuple of positive integers. If
![]() $\alpha =(\alpha _1,\ldots ,\alpha _k)$
is a composition such that
$\alpha =(\alpha _1,\ldots ,\alpha _k)$
is a composition such that
![]() $\alpha _1+\cdots +\alpha _k=n$
, then we say
$\alpha _1+\cdots +\alpha _k=n$
, then we say
![]() $\alpha $
is a composition of n and write
$\alpha $
is a composition of n and write
![]() $\alpha \vDash n$
; the integers
$\alpha \vDash n$
; the integers
![]() $\alpha _i$
are called the
$\alpha _i$
are called the ![]() of
of
![]() $\alpha $
. If
$\alpha $
. If
![]() $\alpha _1\geq \dots \geq \alpha _k$
, then we say
$\alpha _1\geq \dots \geq \alpha _k$
, then we say
![]() $\alpha $
is a
$\alpha $
is a ![]() of n and write
of n and write
![]() $\alpha \vdash n$
. The
$\alpha \vdash n$
. The ![]() of
of
![]() $\alpha $
is the set
$\alpha $
is the set
![]() $\mathrm {Des}(\alpha )=\{\alpha _1, \alpha _1+\alpha _2, \ldots , \alpha _1 + \alpha _2 + \dots + \alpha _{k-1}\}$
. The map
$\mathrm {Des}(\alpha )=\{\alpha _1, \alpha _1+\alpha _2, \ldots , \alpha _1 + \alpha _2 + \dots + \alpha _{k-1}\}$
. The map
![]() $\alpha \mapsto \mathrm {Des}(\alpha )$
is a bijection from the set of compositions of n to the set of subsets of
$\alpha \mapsto \mathrm {Des}(\alpha )$
is a bijection from the set of compositions of n to the set of subsets of
![]() $[n-1]$
.
$[n-1]$
.
For
![]() $\alpha \vDash n$
, the
$\alpha \vDash n$
, the ![]()
![]() $F_\alpha $
is defined by
$F_\alpha $
is defined by
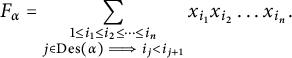 $$\begin{align*}F_\alpha = \sum_{\substack{1\le i_1 \le i_2 \le \dots \le i_n\\ j\in \mathrm{Des}(\alpha) \implies i_j<i_{j+1}}}x_{i_1}x_{i_2}\dots x_{i_n}.\end{align*}$$
$$\begin{align*}F_\alpha = \sum_{\substack{1\le i_1 \le i_2 \le \dots \le i_n\\ j\in \mathrm{Des}(\alpha) \implies i_j<i_{j+1}}}x_{i_1}x_{i_2}\dots x_{i_n}.\end{align*}$$
As
![]() $\alpha $
ranges over all compositions, the fundamental quasisymmetric functions
$\alpha $
ranges over all compositions, the fundamental quasisymmetric functions
![]() $F_{\alpha }$
form a linear basis of the algebra
$F_{\alpha }$
form a linear basis of the algebra
![]() $\mathrm {QSym}$
of quasisymmetric functions. It will be notationally simpler for us to index fundamental quasisymmetric functions (and their variants) by sets instead of compositions. Thus, we will write
$\mathrm {QSym}$
of quasisymmetric functions. It will be notationally simpler for us to index fundamental quasisymmetric functions (and their variants) by sets instead of compositions. Thus, we will write
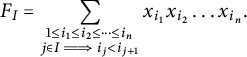 $$\begin{align*}F_I = \sum_{\substack{1\le i_1 \le i_2 \le \dots \le i_n\\ j\in I \implies i_j<i_{j+1}}}x_{i_1}x_{i_2}\dots x_{i_n}.\end{align*}$$
$$\begin{align*}F_I = \sum_{\substack{1\le i_1 \le i_2 \le \dots \le i_n\\ j\in I \implies i_j<i_{j+1}}}x_{i_1}x_{i_2}\dots x_{i_n}.\end{align*}$$
Note that this definition depends implicitly on n; this should not lead to confusion since n will often be fixed.
Example 2.1 Let
![]() $n=4$
. The composition
$n=4$
. The composition
![]() $\alpha =(2,1,1)$
has descent set
$\alpha =(2,1,1)$
has descent set
![]() $\{2,3\}$
, so
$\{2,3\}$
, so
Chow [Reference Chow7] introduced type-B analogs of the fundamental quasisymmetric functions that involve an additional variable
![]() $x_0$
. A
$x_0$
. A ![]() of n is a tuple
of n is a tuple
![]() $(\alpha _1,\ldots ,\alpha _k)$
of integers such that
$(\alpha _1,\ldots ,\alpha _k)$
of integers such that
![]() $\alpha _1\geq 0$
and
$\alpha _1\geq 0$
and
![]() $\alpha _2,\ldots ,\alpha _k\geq 1$
. As for ordinary (type-A) compositions, the descent set of
$\alpha _2,\ldots ,\alpha _k\geq 1$
. As for ordinary (type-A) compositions, the descent set of
![]() $\alpha $
is the set
$\alpha $
is the set
![]() $\mathrm {Des}(\alpha )=\{\alpha _1, \alpha _1+\alpha _2, \ldots , \alpha _1 + \alpha _2 + \dots + \alpha _{k-1}\}$
. The
$\mathrm {Des}(\alpha )=\{\alpha _1, \alpha _1+\alpha _2, \ldots , \alpha _1 + \alpha _2 + \dots + \alpha _{k-1}\}$
. The ![]()
![]() $F_\alpha ^B$
is defined by
$F_\alpha ^B$
is defined by
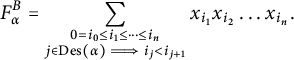 $$\begin{align*}F^B_\alpha = \sum_{\substack{0=i_0\le i_1 \le \dots \le i_n\\ j\in \mathrm{Des}(\alpha) \implies i_j<i_{j+1}}}x_{i_1}x_{i_2}\dots x_{i_n}.\end{align*}$$
$$\begin{align*}F^B_\alpha = \sum_{\substack{0=i_0\le i_1 \le \dots \le i_n\\ j\in \mathrm{Des}(\alpha) \implies i_j<i_{j+1}}}x_{i_1}x_{i_2}\dots x_{i_n}.\end{align*}$$
Note that
![]() $x_0$
appears in
$x_0$
appears in
![]() $F^B_\alpha $
if and only if
$F^B_\alpha $
if and only if
![]() $0$
is not a part of
$0$
is not a part of
![]() $\alpha $
. As before, we will often abuse notation and index type-B quasisymmetric functions with sets; we write
$\alpha $
. As before, we will often abuse notation and index type-B quasisymmetric functions with sets; we write
![]() $F_{\mathrm {Des}(\alpha )}^B$
instead of
$F_{\mathrm {Des}(\alpha )}^B$
instead of
![]() $F_\alpha ^B$
. Again, this notation suppresses the implicit dependence on n.
$F_\alpha ^B$
. Again, this notation suppresses the implicit dependence on n.
Example 2.2 Let
![]() $n=4$
. Then
$n=4$
. Then
and
A subset
![]() $P\subseteq [n-1]$
is called a
$P\subseteq [n-1]$
is called a ![]() if
if
![]() $1\notin P$
and P does not contain two consecutive integers. The compositions whose descent sets are peak sets are called
$1\notin P$
and P does not contain two consecutive integers. The compositions whose descent sets are peak sets are called ![]() ; these are precisely the compositions whose non-final parts are all greater than
; these are precisely the compositions whose non-final parts are all greater than
![]() $1$
. Given a peak set
$1$
. Given a peak set
![]() $P\subseteq [n-1]$
, the
$P\subseteq [n-1]$
, the ![]()
![]() $K_P$
is defined as
$K_P$
is defined as
 $$\begin{align*}K_P = 2^{|P|+1}\sum_{\substack{J\subseteq [n-1] \\ P\subseteq J\triangle (J+1)}} F_J,\end{align*}$$
$$\begin{align*}K_P = 2^{|P|+1}\sum_{\substack{J\subseteq [n-1] \\ P\subseteq J\triangle (J+1)}} F_J,\end{align*}$$
where
![]() $J+1 = \{j+1 : j\in J\}$
and
$J+1 = \{j+1 : j\in J\}$
and
![]() $\triangle $
denotes symmetric difference.
$\triangle $
denotes symmetric difference.
Petersen introduced type-B analogs of the peak functions in [Reference Petersen15]. A subset
![]() ${P\subseteq [n-1]}$
is called a
${P\subseteq [n-1]}$
is called a ![]() if P contains no two consecutive integers; note that a type-B peak set is permitted to contain
if P contains no two consecutive integers; note that a type-B peak set is permitted to contain
![]() $1$
. For each type-B peak set P, there are two type-B peak functions
$1$
. For each type-B peak set P, there are two type-B peak functions
![]() $K_{(0,P)}$
and
$K_{(0,P)}$
and
![]() $K_{(1,P)}$
defined by
$K_{(1,P)}$
defined by
 $$\begin{align*}K_{(0,P)} = 2^{|P|}\sum_{\substack{J\subseteq [0,n-1] \\ P\subseteq J\triangle (J+1)}} F^B_J \quad \mbox{and} \quad K_{(1,P)} = 2^{|P|+1}\sum_{\substack{0\in J \subseteq [0,n-1] \\ P\subseteq J\triangle (J+1)}}F^B_J,\end{align*}$$
$$\begin{align*}K_{(0,P)} = 2^{|P|}\sum_{\substack{J\subseteq [0,n-1] \\ P\subseteq J\triangle (J+1)}} F^B_J \quad \mbox{and} \quad K_{(1,P)} = 2^{|P|+1}\sum_{\substack{0\in J \subseteq [0,n-1] \\ P\subseteq J\triangle (J+1)}}F^B_J,\end{align*}$$
with the proviso that
![]() $K_{(1,P)}$
is defined only if
$K_{(1,P)}$
is defined only if
![]() $1\notin P$
. The type-B peak set associated with a set
$1\notin P$
. The type-B peak set associated with a set
![]() $I\subseteq [0,n-1]$
is
$I\subseteq [0,n-1]$
is
Let us define
where
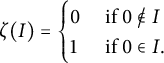 $$\begin{align*}\zeta(I)=\begin{cases} 0 & \mbox{ if } 0\not\in I \\ 1 & \mbox{ if } 0\in I. \end{cases}\end{align*}$$
$$\begin{align*}\zeta(I)=\begin{cases} 0 & \mbox{ if } 0\not\in I \\ 1 & \mbox{ if } 0\in I. \end{cases}\end{align*}$$
We will also make use of the ![]() of I, which we define to be
of I, which we define to be
Note that
2.2 0-Hecke algebras and modules
Given symbols
![]() $\gamma ,\delta $
and a non-negative integer r, we write
$\gamma ,\delta $
and a non-negative integer r, we write
![]() $[\gamma \vert \delta ]_r$
for the word
$[\gamma \vert \delta ]_r$
for the word
 $$\begin{align*}\underbrace{\dots\gamma\delta}_r\end{align*}$$
$$\begin{align*}\underbrace{\dots\gamma\delta}_r\end{align*}$$
of length r that alternates between
![]() $\gamma $
and
$\gamma $
and
![]() $\delta $
and ends with
$\delta $
and ends with
![]() $\delta $
. For example,
$\delta $
. For example,
![]() ${[\gamma \vert \delta ]_4=\gamma \delta \gamma \delta }$
, while
${[\gamma \vert \delta ]_4=\gamma \delta \gamma \delta }$
, while
![]() $[\gamma \vert \delta ]_5=\delta \gamma \delta \gamma \delta $
.
$[\gamma \vert \delta ]_5=\delta \gamma \delta \gamma \delta $
.
Let
![]() $(W,S)$
be a Coxeter system. Thus, W is generated by S, and each element of S is an involution. For all distinct
$(W,S)$
be a Coxeter system. Thus, W is generated by S, and each element of S is an involution. For all distinct
![]() $s,t\in S$
, there is an integer
$s,t\in S$
, there is an integer
![]() $m(s,t)=m(t,s)\in \{2,3,\ldots \}\cup \{\infty \}$
such that
$m(s,t)=m(t,s)\in \{2,3,\ldots \}\cup \{\infty \}$
such that
![]() $[s\vert t]_{m(s,t)}=[t\vert s]_{m(s,t)}$
(this relation is not present if
$[s\vert t]_{m(s,t)}=[t\vert s]_{m(s,t)}$
(this relation is not present if
![]() $m(s,t)=\infty $
). The symmetric group
$m(s,t)=\infty $
). The symmetric group
![]() $S_n$
has the simple generating set
$S_n$
has the simple generating set
![]() $\{s_1,\ldots ,s_{n-1}\}$
, where
$\{s_1,\ldots ,s_{n-1}\}$
, where
![]() $m(s_i,s_{i+1})=3$
for all
$m(s_i,s_{i+1})=3$
for all
![]() $1\leq i\leq n-2$
and
$1\leq i\leq n-2$
and
![]() $m(s_i,s_j)=2$
whenever
$m(s_i,s_j)=2$
whenever
![]() $|i-j|\geq 2$
. The hyperoctahedral group
$|i-j|\geq 2$
. The hyperoctahedral group
![]() $B_n$
has the simple generating set
$B_n$
has the simple generating set
![]() $\{s_0,s_1,\ldots ,s_{n-1}\}$
, where
$\{s_0,s_1,\ldots ,s_{n-1}\}$
, where
![]() $m(s_0,s_1)=4$
,
$m(s_0,s_1)=4$
,
![]() $m(s_0,s_j)=2$
for all
$m(s_0,s_j)=2$
for all
![]() $j\geq 2$
, and
$j\geq 2$
, and
![]() $m(s_i,s_j)$
is the same as for the symmetric group when
$m(s_i,s_j)$
is the same as for the symmetric group when
![]() $i,j\geq 1$
.
$i,j\geq 1$
.
The ![]()
![]() $H_W(0)$
of the Coxeter system
$H_W(0)$
of the Coxeter system
![]() $(W,S)$
is a certain deformation of the group algebra of W; it has a generating set
$(W,S)$
is a certain deformation of the group algebra of W; it has a generating set
![]() $\{\pi _s : s\in S\}$
satisfying the relations
$\{\pi _s : s\in S\}$
satisfying the relations
for all distinct
![]() $s,t\in S$
.
$s,t\in S$
.
We will mostly focus on
![]() $0$
-Hecke algebras when W is
$0$
-Hecke algebras when W is
![]() $S_n$
or
$S_n$
or
![]() $B_n$
. These are referred to as, respectively, the type-A
$B_n$
. These are referred to as, respectively, the type-A
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $H_n(0)$
and the type-B
$H_n(0)$
and the type-B
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $H_n^B(0)$
. The type-A
$H_n^B(0)$
. The type-A
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $H_n(0)$
is generated by
$H_n(0)$
is generated by
![]() $\{\pi _1, \ldots , \pi _{n-1}\}$
satisfying the relations
$\{\pi _1, \ldots , \pi _{n-1}\}$
satisfying the relations
while the type-B
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $H_n^B(0)$
is generated by
$H_n^B(0)$
is generated by
![]() $\{\pi _0, \pi _1, \ldots , \pi _{n-1}\}$
with the same relations (2.3), (2.4), and (2.5) for
$\{\pi _0, \pi _1, \ldots , \pi _{n-1}\}$
with the same relations (2.3), (2.4), and (2.5) for
![]() $1\le i \le n-1$
and the additional relations
$1\le i \le n-1$
and the additional relations
By [Reference Norton13], the simple modules of
![]() $H_n(0)$
(respectively,
$H_n(0)$
(respectively,
![]() $H_n^B(0)$
) are all one-dimensional, and they are in bijection with the subsets of the set of simple generators of
$H_n^B(0)$
) are all one-dimensional, and they are in bijection with the subsets of the set of simple generators of
![]() $S_n$
(respectively,
$S_n$
(respectively,
![]() $B_n$
). For
$B_n$
). For
![]() $I\subseteq [n-1]$
, let us (slightly abusing notation) write
$I\subseteq [n-1]$
, let us (slightly abusing notation) write
![]() $\mathcal S_I$
for the simple
$\mathcal S_I$
for the simple
![]() $H_n(0)$
-module corresponding to the set
$H_n(0)$
-module corresponding to the set
![]() $\{s_i:i\in I\}$
of simple generators of
$\{s_i:i\in I\}$
of simple generators of
![]() $S_n$
. Similarly, for
$S_n$
. Similarly, for
![]() $I\subseteq [0,n-1]$
, we write
$I\subseteq [0,n-1]$
, we write
![]() $\mathcal S_I^B$
for the simple
$\mathcal S_I^B$
for the simple
![]() $H_n^B(0)$
-module corresponding to the set
$H_n^B(0)$
-module corresponding to the set
![]() $\{s_i:i\in I\}$
of simple generators of
$\{s_i:i\in I\}$
of simple generators of
![]() $B_n$
. The module structures of
$B_n$
. The module structures of
![]() $\mathcal S_I$
and
$\mathcal S_I$
and
![]() $\mathcal S_I^B$
are determined by
$\mathcal S_I^B$
are determined by
 $$\begin{align*}\pi_j\varepsilon_I = \begin{cases} -\varepsilon_I & \mbox{ if } j\in I \\ 0 & \mbox{ if } j\notin I, \end{cases}\end{align*}$$
$$\begin{align*}\pi_j\varepsilon_I = \begin{cases} -\varepsilon_I & \mbox{ if } j\in I \\ 0 & \mbox{ if } j\notin I, \end{cases}\end{align*}$$
where
![]() $\varepsilon _I$
is a fixed basis element of
$\varepsilon _I$
is a fixed basis element of
![]() $\mathcal S_I$
or
$\mathcal S_I$
or
![]() $\mathcal S_I^B$
.
$\mathcal S_I^B$
.
Let
![]() $[M]$
denote the isomorphism class of a
$[M]$
denote the isomorphism class of a
![]() $0$
-Hecke module M. The
$0$
-Hecke module M. The ![]() of
of
![]() $H_n(0)$
, denoted
$H_n(0)$
, denoted
![]() $\mathcal {G}_0(H_n(0))$
, is the span of the isomorphism classes of the finitely-generated
$\mathcal {G}_0(H_n(0))$
, is the span of the isomorphism classes of the finitely-generated
![]() $H_n(0)$
-modules, modulo the relation
$H_n(0)$
-modules, modulo the relation
![]() $[A]-[B]+[C]=0$
whenever there exists a short exact sequence
$[A]-[B]+[C]=0$
whenever there exists a short exact sequence
![]() $0\rightarrow A \rightarrow B \rightarrow C\rightarrow 0$
; the Grothendieck group
$0\rightarrow A \rightarrow B \rightarrow C\rightarrow 0$
; the Grothendieck group
![]() $\mathcal {G}_0(H_n^B(0))$
is defined analogously. The (type-A)
$\mathcal {G}_0(H_n^B(0))$
is defined analogously. The (type-A) ![]()
![]() $\mathrm {ch}: \bigoplus _{n\ge 0} \mathcal {G}_0(H_n(0)) \rightarrow \mathrm {QSym}$
[Reference Duchamp, Krob, Leclerc and Thibon8] is the isomorphism defined by
$\mathrm {ch}: \bigoplus _{n\ge 0} \mathcal {G}_0(H_n(0)) \rightarrow \mathrm {QSym}$
[Reference Duchamp, Krob, Leclerc and Thibon8] is the isomorphism defined by
![]() $\mathrm {ch}([\mathcal S_I]) = F_I$
. The
$\mathrm {ch}([\mathcal S_I]) = F_I$
. The ![]()
![]() $\mathrm {ch}^B:\mathcal {G}_0(H_n^B(0))\rightarrow \mathrm {QSym}^B$
is defined by
$\mathrm {ch}^B:\mathcal {G}_0(H_n^B(0))\rightarrow \mathrm {QSym}^B$
is defined by
![]() $\mathrm {ch}^B([\mathcal S_I^B]) = F_I^B$
. For ease of notation, we will generally write
$\mathrm {ch}^B([\mathcal S_I^B]) = F_I^B$
. For ease of notation, we will generally write
![]() $\mathrm {ch}(M)$
in place of
$\mathrm {ch}(M)$
in place of
![]() $\mathrm {ch}([M])$
.
$\mathrm {ch}([M])$
.
3 Ascent-compatibility
Let
![]() $(W,S)$
be a Coxeter system. A
$(W,S)$
be a Coxeter system. A ![]() for an element
for an element
![]() $w\in W$
is a minimum-length word over the alphabet S that represents w; the number of letters in a reduced word for w is called the
$w\in W$
is a minimum-length word over the alphabet S that represents w; the number of letters in a reduced word for w is called the ![]() of w and is denoted by
of w and is denoted by
![]() $\ell (w)$
. We say
$\ell (w)$
. We say
![]() $s\in S$
is a (left)
$s\in S$
is a (left) ![]() of w if
of w if
![]() $\ell (sw)<\ell (w)$
; otherwise, s is an
$\ell (sw)<\ell (w)$
; otherwise, s is an ![]() of w. The set of descents of w is denoted
of w. The set of descents of w is denoted
![]() $\mathrm {Des}(w)$
.
$\mathrm {Des}(w)$
.
Given an arbitrary set X, we write
![]() $\mathbb CX$
for the complex vector space freely generated by X.
$\mathbb CX$
for the complex vector space freely generated by X.
Fix
![]() $X\subseteq W$
. For
$X\subseteq W$
. For
![]() $s\in S$
, define a linear operator
$s\in S$
, define a linear operator
![]() $ \pi _s: \mathbb C X \rightarrow \mathbb C X$
by
$ \pi _s: \mathbb C X \rightarrow \mathbb C X$
by
 $$\begin{align*}\pi_s(x) = \begin{cases} -x & \mbox{ if } s\in \mathrm{Des}(x) \\ 0 & \mbox{ if } s\notin \mathrm{Des}(x) \mbox{ and } sx\notin X \\ sx & \mbox{ if } s\notin \mathrm{Des}(x) \mbox{ and } sx\in X \end{cases}\end{align*}$$
$$\begin{align*}\pi_s(x) = \begin{cases} -x & \mbox{ if } s\in \mathrm{Des}(x) \\ 0 & \mbox{ if } s\notin \mathrm{Des}(x) \mbox{ and } sx\notin X \\ sx & \mbox{ if } s\notin \mathrm{Des}(x) \mbox{ and } sx\in X \end{cases}\end{align*}$$
for all
![]() $x\in X$
. For
$x\in X$
. For
![]() $u,v\in W$
and
$u,v\in W$
and
![]() $s,t\in S$
, let us say the quadruple
$s,t\in S$
, let us say the quadruple
![]() $(u,v,s,t)$
is
$(u,v,s,t)$
is ![]() if the simple generator s is an ascent of u, the simple generator t is an ascent of v, and
if the simple generator s is an ascent of u, the simple generator t is an ascent of v, and
![]() $u^{-1}su=v^{-1}tv$
. We say X is
$u^{-1}su=v^{-1}tv$
. We say X is ![]() if for all
if for all
![]() $u,v \in X$
and all
$u,v \in X$
and all
![]() $s,t\in S$
such that
$s,t\in S$
such that
![]() $(u,v,s,t)$
is aligned, we have that
$(u,v,s,t)$
is aligned, we have that
![]() $su\in X$
if and only if
$su\in X$
if and only if
![]() $tv\in X$
.
$tv\in X$
.
The following theorem was proven in type A in [Reference Searles17], where it was used to provide a general framework for constructing type-A 0-Hecke modules whose quasisymmetric characteristics are interesting quasisymmetric functions.
Theorem 3.1 Let
![]() $(W,S)$
be a Coxeter system. If X is an ascent-compatible subset of W, then the linear operators
$(W,S)$
be a Coxeter system. If X is an ascent-compatible subset of W, then the linear operators
![]() $\pi _s$
define an action of the
$\pi _s$
define an action of the
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $H_W(0)$
on
$H_W(0)$
on
![]() $\mathbb C X$
.
$\mathbb C X$
.
Proof Fix
![]() $x\in X$
and
$x\in X$
and
![]() $s\in S$
. We first show that
$s\in S$
. We first show that
![]() $ \pi _s^2(x)=- \pi _s(x)$
. If
$ \pi _s^2(x)=- \pi _s(x)$
. If
![]() $ \pi _s(x)=-x$
, then we have
$ \pi _s(x)=-x$
, then we have
![]() $ \pi _s^2(x)= \pi _s(-x)=- \pi _s(x)$
. If
$ \pi _s^2(x)= \pi _s(-x)=- \pi _s(x)$
. If
![]() $ \pi _s(x)=0$
, then
$ \pi _s(x)=0$
, then
![]() $ \pi _s^2(x)=0=- \pi _s(x)$
. If
$ \pi _s^2(x)=0=- \pi _s(x)$
. If
![]() $ \pi _s^2(x)=sx$
, then
$ \pi _s^2(x)=sx$
, then
![]() $s\not \in \mathrm {Des}(x)$
, so
$s\not \in \mathrm {Des}(x)$
, so
![]() $s\in \mathrm {Des}(sx)$
. In this case,
$s\in \mathrm {Des}(sx)$
. In this case,
![]() $ \pi _s^2(x)= \pi _s(sx)=-sx=- \pi _s(x)$
.
$ \pi _s^2(x)= \pi _s(sx)=-sx=- \pi _s(x)$
.
Now choose some
![]() $t\in S\setminus \{s\}$
, and let
$t\in S\setminus \{s\}$
, and let
![]() $m=m(s,t)$
. We need to show that
$m=m(s,t)$
. We need to show that
![]() ${[{\pi }_s\vert {\pi }_t]_m(x)=[{\pi }_t\vert {\pi }_s]_m(x)}$
. We consider two cases.
${[{\pi }_s\vert {\pi }_t]_m(x)=[{\pi }_t\vert {\pi }_s]_m(x)}$
. We consider two cases.
Case 1. Suppose either
![]() $s\in \mathrm {Des}(x)$
or
$s\in \mathrm {Des}(x)$
or
![]() $t\in \mathrm {Des}(x)$
. Without loss of generality, we may assume
$t\in \mathrm {Des}(x)$
. Without loss of generality, we may assume
![]() $s\in \mathrm {Des}(x)$
. Then,
$s\in \mathrm {Des}(x)$
. Then,
![]() ${\pi }_s(x)=-x$
, so
${\pi }_s(x)=-x$
, so
![]() $[{\pi }_s\vert {\pi }_t]_i(x)=-[{\pi }_t\vert {\pi }_s]_{i+1}(x)$
for all
$[{\pi }_s\vert {\pi }_t]_i(x)=-[{\pi }_t\vert {\pi }_s]_{i+1}(x)$
for all
![]() $i\geq 0$
. Let k be the largest integer in
$i\geq 0$
. Let k be the largest integer in
![]() $[0,m-1]$
such that
$[0,m-1]$
such that
![]() $[{\pi }_s\vert {\pi }_t]_k(x)=[s\vert t]_kx$
. Let
$[{\pi }_s\vert {\pi }_t]_k(x)=[s\vert t]_kx$
. Let
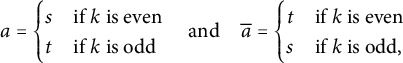 $$\begin{align*}a=\begin{cases} s & \mbox{if } k\text{ is even} \\ t & \mbox{if } k\text{ is odd}\end{cases}\quad\text{and}\quad \overline a=\begin{cases} t & \mbox{if } k\text{ is even} \\ s & \mbox{if } k\text{ is odd,}\end{cases}\end{align*}$$
$$\begin{align*}a=\begin{cases} s & \mbox{if } k\text{ is even} \\ t & \mbox{if } k\text{ is odd}\end{cases}\quad\text{and}\quad \overline a=\begin{cases} t & \mbox{if } k\text{ is even} \\ s & \mbox{if } k\text{ is odd,}\end{cases}\end{align*}$$
and observe that
![]() $a\in \mathrm {Des}([s\vert t]_kx)$
. If we assume that
$a\in \mathrm {Des}([s\vert t]_kx)$
. If we assume that
![]() $k\leq m-2$
and
$k\leq m-2$
and
![]() $[{\pi }_s\vert {\pi }_t]_{k+1}(x)=0$
, then
$[{\pi }_s\vert {\pi }_t]_{k+1}(x)=0$
, then
![]() ${[{\pi }_t\vert {\pi }_s]_{k+2}(x)=-[{\pi }_s\vert {\pi }_t]_{k+1}(x)=0}$
, so
${[{\pi }_t\vert {\pi }_s]_{k+2}(x)=-[{\pi }_s\vert {\pi }_t]_{k+1}(x)=0}$
, so
![]() ${[{\pi }_s\vert {\pi }_t]_m(x)=0=[{\pi }_t\vert {\pi }_s]_m(x)}$
. Hence, we may assume either that
${[{\pi }_s\vert {\pi }_t]_m(x)=0=[{\pi }_t\vert {\pi }_s]_m(x)}$
. Hence, we may assume either that
![]() $k=m-1$
or that
$k=m-1$
or that
![]() $k\leq m-2$
and
$k\leq m-2$
and
![]() $[{\pi }_s\vert {\pi }_t]_{k+1}(x)=-[s\vert t]_kx$
. We claim that
$[{\pi }_s\vert {\pi }_t]_{k+1}(x)=-[s\vert t]_kx$
. We claim that
![]() $\overline a\in \mathrm {Des}([s\vert t]_kx)$
. This is immediate from the definitions of k and
$\overline a\in \mathrm {Des}([s\vert t]_kx)$
. This is immediate from the definitions of k and
![]() ${\pi }_{\overline a}$
if
${\pi }_{\overline a}$
if
![]() $[{\pi }_s\vert {\pi }_t]_{k+1}(x)=-[s\vert t]_kx$
. Now suppose
$[{\pi }_s\vert {\pi }_t]_{k+1}(x)=-[s\vert t]_kx$
. Now suppose
![]() $k=m-1$
. Since
$k=m-1$
. Since
![]() $s\in \mathrm {Des}(x)$
, we can write
$s\in \mathrm {Des}(x)$
, we can write
![]() $x=sy$
, where
$x=sy$
, where
![]() $\ell (x)=\ell (y)+1$
. Then
$\ell (x)=\ell (y)+1$
. Then
![]() $[s\vert t]_{m-1}x=[t\vert s]_my=[s\vert t]_my$
, and
$[s\vert t]_{m-1}x=[t\vert s]_my=[s\vert t]_my$
, and
![]() $\ell ([s\vert t]_my)=\ell (y)+m$
. The first letter in the word
$\ell ([s\vert t]_my)=\ell (y)+m$
. The first letter in the word
![]() $[s\vert t]_my$
is
$[s\vert t]_my$
is
![]() $\overline a$
, so
$\overline a$
, so
![]() $\overline a\in \mathrm {Des}([s\vert t]_my)=\mathrm {Des}([s\vert t]_{k}x)$
.
$\overline a\in \mathrm {Des}([s\vert t]_my)=\mathrm {Des}([s\vert t]_{k}x)$
.
We have proven that
![]() $\{s,t\}=\{a,\overline a\}\subseteq \mathrm {Des}([s\vert t]_kx)$
, so
$\{s,t\}=\{a,\overline a\}\subseteq \mathrm {Des}([s\vert t]_kx)$
, so
![]() $[{\pi }_s\vert {\pi }_t]_m(x)=(-1)^{m-k}[s\vert t]_k(x)$
and
$[{\pi }_s\vert {\pi }_t]_m(x)=(-1)^{m-k}[s\vert t]_k(x)$
and
![]() $[{\pi }_t\vert {\pi }_s]_m(x)=-[{\pi }_s\vert {\pi }_t]_{m-1}(x)=-(-1)^{m-1-k}[s\vert t]_k(x)$
. Thus,
$[{\pi }_t\vert {\pi }_s]_m(x)=-[{\pi }_s\vert {\pi }_t]_{m-1}(x)=-(-1)^{m-1-k}[s\vert t]_k(x)$
. Thus,
![]() $[{\pi }_s\vert {\pi }_t]_m(x)=[{\pi }_t\vert {\pi }_s]_m(x)$
.
$[{\pi }_s\vert {\pi }_t]_m(x)=[{\pi }_t\vert {\pi }_s]_m(x)$
.
Case 2. Suppose
![]() $s,t\not \in \mathrm {Des}(x)$
. Since
$s,t\not \in \mathrm {Des}(x)$
. Since
![]() $[s\vert t]_m$
is the longest element of the parabolic subgroup of W generated by
$[s\vert t]_m$
is the longest element of the parabolic subgroup of W generated by
![]() $\{s,t\}$
, it follows from [Reference Björner and Brenti5, Lemma 3.2.4] that
$\{s,t\}$
, it follows from [Reference Björner and Brenti5, Lemma 3.2.4] that
![]() $\ell ([s\vert t]_mx)=\ell (x)+m$
. This implies that
$\ell ([s\vert t]_mx)=\ell (x)+m$
. This implies that
![]() $[{\pi }_s\vert {\pi }_t]_m(x)\in \{0,[s\vert t]_mx\}$
and
$[{\pi }_s\vert {\pi }_t]_m(x)\in \{0,[s\vert t]_mx\}$
and
![]() $[{\pi }_t,{\pi }_s]_m(x)\in \{0,[t\vert s]_mx\}=\{0,[t\vert s]_mx\}$
. Assume by way of contradiction that
$[{\pi }_t,{\pi }_s]_m(x)\in \{0,[t\vert s]_mx\}=\{0,[t\vert s]_mx\}$
. Assume by way of contradiction that
![]() $[{\pi }_s,\vert {\pi }_t]_m(x)\neq [{\pi }_t\vert {\pi }_s]_m(x)$
. Without loss of generality, we may assume that
$[{\pi }_s,\vert {\pi }_t]_m(x)\neq [{\pi }_t\vert {\pi }_s]_m(x)$
. Without loss of generality, we may assume that
![]() $[{\pi }_s\vert {\pi }_t]_m(x)=0$
and
$[{\pi }_s\vert {\pi }_t]_m(x)=0$
and
![]() $[{\pi }_t\vert {\pi }_s]_m(x)=[s\vert t]_mx$
. There exists
$[{\pi }_t\vert {\pi }_s]_m(x)=[s\vert t]_mx$
. There exists
![]() $j\in [0,m-1]$
such that
$j\in [0,m-1]$
such that
![]() ${[{\pi }_s\vert {\pi }_t]_j(x)\neq 0=[{\pi }_s\vert {\pi }_t]_{j+1}(x)}$
. Let
${[{\pi }_s\vert {\pi }_t]_j(x)\neq 0=[{\pi }_s\vert {\pi }_t]_{j+1}(x)}$
. Let
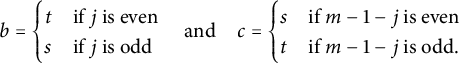 $$\begin{align*}b=\begin{cases} t & \mbox{if } j\text{ is even} \\ s & \mbox{if } j\text{ is odd}\end{cases}\quad\text{and}\quad c=\begin{cases} s & \mbox{if } m-1-j\text{ is even} \\ t & \mbox{if } m-1-j\text{ is odd.}\end{cases}\end{align*}$$
$$\begin{align*}b=\begin{cases} t & \mbox{if } j\text{ is even} \\ s & \mbox{if } j\text{ is odd}\end{cases}\quad\text{and}\quad c=\begin{cases} s & \mbox{if } m-1-j\text{ is even} \\ t & \mbox{if } m-1-j\text{ is odd.}\end{cases}\end{align*}$$
Then,
 $$ \begin{align*} ([s\vert t]_jx)^{-1}b([s\vert t]_jx)&=x^{-1}[s\vert t]_{2j+1}x \\ &=x^{-1}[t\vert s]_{2m-2j-1}x \\ &=([t\vert s]_{m-1-j}x)^{-1}c([t\vert s]_{m-1-j}x), \end{align*} $$
$$ \begin{align*} ([s\vert t]_jx)^{-1}b([s\vert t]_jx)&=x^{-1}[s\vert t]_{2j+1}x \\ &=x^{-1}[t\vert s]_{2m-2j-1}x \\ &=([t\vert s]_{m-1-j}x)^{-1}c([t\vert s]_{m-1-j}x), \end{align*} $$
and we have
This shows that the quadruple
![]() $([s\vert t]_jx,[t\vert s]_{m-1-j}x,b,c)$
is aligned. Furthermore, we know that
$([s\vert t]_jx,[t\vert s]_{m-1-j}x,b,c)$
is aligned. Furthermore, we know that
![]() ${\pi }_b([s\vert t]_jx)=[{\pi }_s\vert {\pi }_t]_{j+1}(x)=0$
, so
${\pi }_b([s\vert t]_jx)=[{\pi }_s\vert {\pi }_t]_{j+1}(x)=0$
, so
![]() $b[s\vert t]_jx\not \in X$
. Because X is ascent-compatible, we must have
$b[s\vert t]_jx\not \in X$
. Because X is ascent-compatible, we must have
![]() ${c[t\vert s]_{m-1-j}x\not \in X}$
, so
${c[t\vert s]_{m-1-j}x\not \in X}$
, so
![]() ${\pi }_c([t\vert s]_{m-1-j}x)=0$
. This is impossible since
${\pi }_c([t\vert s]_{m-1-j}x)=0$
. This is impossible since
![]() ${\pi }_c([t\vert s]_{m-1-j}x)=[{\pi }_t\vert {\pi }_s]_{m-j}(x)$
and
${\pi }_c([t\vert s]_{m-1-j}x)=[{\pi }_t\vert {\pi }_s]_{m-j}(x)$
and
![]() $[{\pi }_t\vert {\pi }_s]_{m}(x)\neq 0$
.
$[{\pi }_t\vert {\pi }_s]_{m}(x)\neq 0$
.
For an easy example of an ascent-compatible set, consider
![]() $I\subseteq S$
, and define the
$I\subseteq S$
, and define the ![]() associated with I to be the set
associated with I to be the set
![]() $D_I^W=\{x\in W:\mathrm {Des}(x)=I\}$
.
$D_I^W=\{x\in W:\mathrm {Des}(x)=I\}$
.
Proposition 3.2 Let
![]() $(W,S)$
be a Coxeter system. If
$(W,S)$
be a Coxeter system. If
![]() $I\subseteq S$
and
$I\subseteq S$
and
![]() $X\subseteq D_I^W$
, then X is ascent-compatible.
$X\subseteq D_I^W$
, then X is ascent-compatible.
Proof Suppose
![]() $u,v\in X$
and
$u,v\in X$
and
![]() $s,t\in S$
are such that
$s,t\in S$
are such that
![]() $(u,v,s,t)$
is aligned. Then,
$(u,v,s,t)$
is aligned. Then,
![]() ${s\not \in \mathrm {Des}(u)=I}$
and
${s\not \in \mathrm {Des}(u)=I}$
and
![]() $t\not \in \mathrm {Des}(v)=I$
. However, we have
$t\not \in \mathrm {Des}(v)=I$
. However, we have
![]() $s\in \mathrm {Des}(su)$
and
$s\in \mathrm {Des}(su)$
and
![]() $t\in \mathrm {Des}(tv)$
, so
$t\in \mathrm {Des}(tv)$
, so
![]() $su$
and
$su$
and
![]() $tv$
are not in
$tv$
are not in
![]() $D_I^W$
. It follows that
$D_I^W$
. It follows that
![]() $su$
and
$su$
and
![]() $tv$
are both not in X.
$tv$
are both not in X.
The next theorem provides more interesting examples of ascent-compatible sets. First, we need to establish some additional background. As before, let
![]() $(W,S)$
be a Coxeter system. For
$(W,S)$
be a Coxeter system. For
![]() $x,y\in W$
, let us write
$x,y\in W$
, let us write
![]() $x\leq _{{\mathsf {L}}}y$
if there is a reduced word for y that contains a reduced word for x as a suffix; then
$x\leq _{{\mathsf {L}}}y$
if there is a reduced word for y that contains a reduced word for x as a suffix; then
![]() $\leq _{{\mathsf {L}}}$
is a partial order on W called the
$\leq _{{\mathsf {L}}}$
is a partial order on W called the ![]() . If
. If
![]() $x\leq _{{\mathsf {L}}}y$
, then the
$x\leq _{{\mathsf {L}}}y$
, then the ![]() between x and y in the left weak order is the set
between x and y in the left weak order is the set
![]() $[x,y]_{{\mathsf {L}}}=\{z\in W:x\leq _{L}z\leq _{{\mathsf {L}}}y\}$
. A set
$[x,y]_{{\mathsf {L}}}=\{z\in W:x\leq _{L}z\leq _{{\mathsf {L}}}y\}$
. A set
![]() $X\subseteq W$
is
$X\subseteq W$
is ![]() (in the left weak order) if for all
(in the left weak order) if for all
![]() $x,y\in X$
with
$x,y\in X$
with
![]() $x\leq _{{\mathsf {L}}}y$
, we have
$x\leq _{{\mathsf {L}}}y$
, we have
![]() $[x,y]_{{\mathsf {L}}}\subseteq X$
. A
$[x,y]_{{\mathsf {L}}}\subseteq X$
. A ![]() in W is an element that is conjugate to a simple generator. Thus, the set of reflections is
in W is an element that is conjugate to a simple generator. Thus, the set of reflections is
![]() $\{w^{-1}sw:s\in S, w\in W\}$
. A reflection r is called a
$\{w^{-1}sw:s\in S, w\in W\}$
. A reflection r is called a ![]() of an element
of an element
![]() $x\in W$
if
$x\in W$
if
![]() $\ell (xr)<\ell (x)$
. Let
$\ell (xr)<\ell (x)$
. Let
![]() $\mathrm {Inv}(x)$
denote the set of right inversions of x. For
$\mathrm {Inv}(x)$
denote the set of right inversions of x. For
![]() $x,y\in W$
, it is well known that
$x,y\in W$
, it is well known that
![]() $\ell (x)=\lvert \mathrm {Inv}(x)\rvert $
and that
$\ell (x)=\lvert \mathrm {Inv}(x)\rvert $
and that
![]() $x\leq _{{\mathsf {L}}}y$
if and only if
$x\leq _{{\mathsf {L}}}y$
if and only if
![]() $\mathrm {Inv}(x)\subseteq \mathrm {Inv}(y)$
.
$\mathrm {Inv}(x)\subseteq \mathrm {Inv}(y)$
.
Theorem 3.3 Let
![]() $(W,S)$
be a Coxeter system, and let
$(W,S)$
be a Coxeter system, and let
![]() $X\subseteq W$
. If X is convex in the left weak order and has a unique maximal element under the left weak order, then X is ascent-compatible.
$X\subseteq W$
. If X is convex in the left weak order and has a unique maximal element under the left weak order, then X is ascent-compatible.
Proof Let z be the unique maximal element of X. Assume by way of contradiction that X is not ascent-compatible. Then there exist
![]() $u,v\in X$
and
$u,v\in X$
and
![]() $s,t\in S$
such that
$s,t\in S$
such that
![]() $(u,v,s,t)$
is aligned,
$(u,v,s,t)$
is aligned,
![]() $su\in X$
, and
$su\in X$
, and
![]() $tv\not \in X$
. Let
$tv\not \in X$
. Let
![]() $r=u^{-1}su=v^{-1}tv$
. Since
$r=u^{-1}su=v^{-1}tv$
. Since
![]() $u\leq _{{\mathsf {L}}} su$
and
$u\leq _{{\mathsf {L}}} su$
and
![]() $v\leq _{{\mathsf {L}}}tv$
, the reflection r is both a right inversion of
$v\leq _{{\mathsf {L}}}tv$
, the reflection r is both a right inversion of
![]() $su$
and a right inversion of
$su$
and a right inversion of
![]() $tv$
. Since
$tv$
. Since
![]() $su\in X$
, we have
$su\in X$
, we have
![]() $su\leq _{{\mathsf {L}}}z$
, so
$su\leq _{{\mathsf {L}}}z$
, so
![]() $\mathrm {Inv}(su)\subseteq \mathrm {Inv}(z)$
. This implies that
$\mathrm {Inv}(su)\subseteq \mathrm {Inv}(z)$
. This implies that
![]() $r\in \mathrm {Inv}(z)$
. On the other hand, since
$r\in \mathrm {Inv}(z)$
. On the other hand, since
![]() $\lvert \mathrm {Inv}(tv)\rvert =\ell (tv)=\ell (v)+1=\lvert \mathrm {Inv}(v)\rvert +1$
and
$\lvert \mathrm {Inv}(tv)\rvert =\ell (tv)=\ell (v)+1=\lvert \mathrm {Inv}(v)\rvert +1$
and
![]() $r\not \in \mathrm {Inv}(v)$
, we must have
$r\not \in \mathrm {Inv}(v)$
, we must have
![]() $\mathrm {Inv}(tv)=\mathrm {Inv}(v)\cup \{r\}$
. Because
$\mathrm {Inv}(tv)=\mathrm {Inv}(v)\cup \{r\}$
. Because
![]() $v\in X$
, we have
$v\in X$
, we have
![]() $v\leq _{{\mathsf {L}}}z$
, so
$v\leq _{{\mathsf {L}}}z$
, so
![]() $\mathrm {Inv}(v)\subseteq \mathrm {Inv}(z)$
. This implies that
$\mathrm {Inv}(v)\subseteq \mathrm {Inv}(z)$
. This implies that
![]() $\mathrm {Inv}(tv)=\mathrm {Inv}(v)\cup \{r\}\subseteq \mathrm {Inv}(z)$
, so
$\mathrm {Inv}(tv)=\mathrm {Inv}(v)\cup \{r\}\subseteq \mathrm {Inv}(z)$
, so
![]() $v\leq _{{\mathsf {L}}}tv\leq _{{\mathsf {L}}}z$
. However, X is convex and contains v and z, so this forces
$v\leq _{{\mathsf {L}}}tv\leq _{{\mathsf {L}}}z$
. However, X is convex and contains v and z, so this forces
![]() $tv$
to belong to X, which is a contradiction.
$tv$
to belong to X, which is a contradiction.
Remark 3.4 Inverses of left descent classes (which are also called right descent classes) provide notable examples of convex subsets of the left weak order of a Coxeter group W. More precisely, if
![]() $(W,S)$
is a Coxeter system and
$(W,S)$
is a Coxeter system and
![]() $I\subseteq S$
is such that the left descent class
$I\subseteq S$
is such that the left descent class
![]() $D_I^W$
is nonempty, then the right descent class
$D_I^W$
is nonempty, then the right descent class
![]() $(D_I^W)^{-1}=\{x\in W:\mathrm {Des}(x^{-1})=I\}$
is a finite convex subset of the left weak order that has a unique maximal element. Hence, if
$(D_I^W)^{-1}=\{x\in W:\mathrm {Des}(x^{-1})=I\}$
is a finite convex subset of the left weak order that has a unique maximal element. Hence, if
![]() $D_I^W$
is nonempty, then
$D_I^W$
is nonempty, then
![]() $(D_I^W)^{-1}$
is ascent-compatible by Theorem 3.3.
$(D_I^W)^{-1}$
is ascent-compatible by Theorem 3.3.
It was shown in [Reference Jung, Kim, Lee and Oh10] that intervals in the left weak order on the symmetric group
![]() $S_n$
give rise to important families of type-A
$S_n$
give rise to important families of type-A
![]() $0$
-Hecke modules, and in [Reference Searles17], it was shown that these modules can be obtained via the ascent-compatibility framework. One can view Theorem 3.3 as a generalization of this to arbitrary Coxeter groups; our theorem is also more general even in type A since it does not require the set X to have a unique minimal element.
$0$
-Hecke modules, and in [Reference Searles17], it was shown that these modules can be obtained via the ascent-compatibility framework. One can view Theorem 3.3 as a generalization of this to arbitrary Coxeter groups; our theorem is also more general even in type A since it does not require the set X to have a unique minimal element.
Let us now specialize our attention to the hyperoctahedral group
![]() $B_n$
and its
$B_n$
and its
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $H_n^B(0)$
. It will be convenient to identify simple generators of
$H_n^B(0)$
. It will be convenient to identify simple generators of
![]() $B_n$
with their indices; for instance, we will view the descent set of an element of
$B_n$
with their indices; for instance, we will view the descent set of an element of
![]() $B_n$
as a subset of
$B_n$
as a subset of
![]() $[0,n-1]$
. If X is an ascent-compatible subset of
$[0,n-1]$
. If X is an ascent-compatible subset of
![]() $S_n$
, then Theorem 3.1 endows
$S_n$
, then Theorem 3.1 endows
![]() $\mathbb C X$
with the structure of an
$\mathbb C X$
with the structure of an
![]() $H_n(0)$
-module. It was proven in [Reference Searles17] that the quasisymmetric characteristic of this module is given by
$H_n(0)$
-module. It was proven in [Reference Searles17] that the quasisymmetric characteristic of this module is given by
The same argument yields the following analog of this result in type B.
Theorem 3.5 If X is an ascent-compatible subset of
![]() $B_n$
, then
$B_n$
, then
Proof Let
![]() $m=|X|$
, and let
$m=|X|$
, and let
![]() $x_m,\ldots ,x_1$
be a linear extension of the poset
$x_m,\ldots ,x_1$
be a linear extension of the poset
![]() $(X,\leq _{{\mathsf {L}}})$
. That is,
$(X,\leq _{{\mathsf {L}}})$
. That is,
![]() $x_m,\ldots ,x_1$
is an ordering of the elements of X such that
$x_m,\ldots ,x_1$
is an ordering of the elements of X such that
![]() $j<i$
whenever
$j<i$
whenever
![]() $x_i\leq _{{\mathsf {L}}}x_j$
. For
$x_i\leq _{{\mathsf {L}}}x_j$
. For
![]() $0\leq k\leq m$
, let
$0\leq k\leq m$
, let
![]() $\textbf {N}_k=\text {span}\{x_1,\ldots ,x_k\}$
. Then
$\textbf {N}_k=\text {span}\{x_1,\ldots ,x_k\}$
. Then
is a filtration of
![]() $\mathbb C X$
. For
$\mathbb C X$
. For
![]() $1\leq k\leq m$
, the quotient
$1\leq k\leq m$
, the quotient
![]() $\textbf {N}_k/\textbf {N}_{k-1}$
is a
$\textbf {N}_k/\textbf {N}_{k-1}$
is a
![]() $1$
-dimensional
$1$
-dimensional
![]() $H_n^B(0)$
-module spanned by the element
$H_n^B(0)$
-module spanned by the element
![]() $\overline x_k=x_k+\textbf {N}_{k-1}$
; the module structure is given by
$\overline x_k=x_k+\textbf {N}_{k-1}$
; the module structure is given by
 $$\begin{align*}\pi_j(\overline x_k)=\begin{cases} -\overline x_k & \mbox{ if } j\in \mathrm{Des}(x_k) \\ 0 & \mbox{ if } j\not\in\mathrm{Des}(x_k). \end{cases} \end{align*}$$
$$\begin{align*}\pi_j(\overline x_k)=\begin{cases} -\overline x_k & \mbox{ if } j\in \mathrm{Des}(x_k) \\ 0 & \mbox{ if } j\not\in\mathrm{Des}(x_k). \end{cases} \end{align*}$$
Thus,
![]() $\textbf {N}_k/\textbf {N}_{k-1}$
is isomorphic to the simple module
$\textbf {N}_k/\textbf {N}_{k-1}$
is isomorphic to the simple module
![]() $\mathcal S_{\mathrm {Des}(x_k)}^B$
. It follows that
$\mathcal S_{\mathrm {Des}(x_k)}^B$
. It follows that
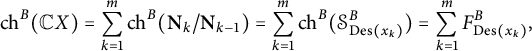 $$\begin{align*}\mathrm{ch}^B(\mathbb C X)=\sum_{k=1}^m\mathrm{ch}^B(\textbf{N}_k/\textbf{N}_{k-1})=\sum_{k=1}^m\mathrm{ch}^B(\mathcal S_{\mathrm{Des}(x_k)}^B)=\sum_{k=1}^m F^B_{\mathrm{Des}(x_k)}, \end{align*}$$
$$\begin{align*}\mathrm{ch}^B(\mathbb C X)=\sum_{k=1}^m\mathrm{ch}^B(\textbf{N}_k/\textbf{N}_{k-1})=\sum_{k=1}^m\mathrm{ch}^B(\mathcal S_{\mathrm{Des}(x_k)}^B)=\sum_{k=1}^m F^B_{\mathrm{Des}(x_k)}, \end{align*}$$
as desired.
In Section 6, we will obtain a result similar to Theorem 3.5 that will allow us to compute the type-B quasisymmetric characteristic of the module obtained from an ascent-compatible set X by first inducing a type-B
![]() $0$
-Hecke–Clifford module from
$0$
-Hecke–Clifford module from
![]() $\mathbb CX$
and then restricting back to an
$\mathbb CX$
and then restricting back to an
![]() $H_n^B(0)$
-module.
$H_n^B(0)$
-module.
We now provide specific applications of Theorem 3.5. Motivated by a type-B analog of Schur positivity, Mayorova and Vassilieva [Reference Mayorova and Vassilieva11] studied several interesting subsets of
![]() $B_n$
and functions associated with them. For
$B_n$
and functions associated with them. For
![]() $X\subseteq B_n$
, let
$X\subseteq B_n$
, let
For a specific choice of X, if we can show that the set
![]() $X^{-1} = \{x^{-1}:x\in X\}$
is ascent-compatible, then it will follow from Theorems 3.1 and 3.5 that
$X^{-1} = \{x^{-1}:x\in X\}$
is ascent-compatible, then it will follow from Theorems 3.1 and 3.5 that
![]() $\mathcal Q(X)$
can be realized as the quasisymmetric characteristic of an
$\mathcal Q(X)$
can be realized as the quasisymmetric characteristic of an
![]() $H_n^B(0)$
-module.
$H_n^B(0)$
-module.
We view
![]() $B_n$
as the group of permutations
$B_n$
as the group of permutations
![]() $\sigma $
of the set
$\sigma $
of the set
![]() $\pm [n]:=\{\pm 1,\ldots ,\pm n\}$
with the property that
$\pm [n]:=\{\pm 1,\ldots ,\pm n\}$
with the property that
![]() ${\sigma (-i)=-\sigma (i)}$
for all i. One example of a set
${\sigma (-i)=-\sigma (i)}$
for all i. One example of a set
![]() $X\subseteq B_n$
whose corresponding function
$X\subseteq B_n$
whose corresponding function
![]() $\mathcal {Q}(X)$
was studied in [Reference Mayorova and Vassilieva11] is the left descent class
$\mathcal {Q}(X)$
was studied in [Reference Mayorova and Vassilieva11] is the left descent class
![]() $D_I^{B} = \{\sigma \in B_n: \mathrm {Des}(\sigma )=I\}$
associated with a set
$D_I^{B} = \{\sigma \in B_n: \mathrm {Des}(\sigma )=I\}$
associated with a set
![]() $I\subseteq [0,n-1]$
(where we identify the simple generator
$I\subseteq [0,n-1]$
(where we identify the simple generator
![]() $s_i$
with the index i). A second example of such a set X is the set
$s_i$
with the index i). A second example of such a set X is the set
![]() $L^B=\bigcup _{i=1}^nL_i^B$
, where
$L^B=\bigcup _{i=1}^nL_i^B$
, where
![]() $L_i^B$
is the set of all
$L_i^B$
is the set of all
![]() $\sigma \in B_n$
such that
$\sigma \in B_n$
such that
elements of
![]() $L^B$
are called
$L^B$
are called ![]() .
.
Theorem 3.6 The sets
![]() $(D_I^{B})^{-1}$
and
$(D_I^{B})^{-1}$
and
![]() $(L_i^B)^{-1}$
are ascent-compatible. Therefore, both
$(L_i^B)^{-1}$
are ascent-compatible. Therefore, both
![]() $\mathbb C(D_I^{B})^{-1}$
and
$\mathbb C(D_I^{B})^{-1}$
and
![]() $\mathbb C(L_i^B)^{-1}$
are
$\mathbb C(L_i^B)^{-1}$
are
![]() $H_n^B(0)$
-modules, and we have
$H_n^B(0)$
-modules, and we have
the latter of these identities implies that
![]() $\mathrm {ch}^B(\bigoplus _{i=1}^n\mathbb C(L_i^B)^{-1})=\mathcal {Q}(L^B)$
.
$\mathrm {ch}^B(\bigoplus _{i=1}^n\mathbb C(L_i^B)^{-1})=\mathcal {Q}(L^B)$
.
Proof We know from Remark 3.4 that
![]() $(D_I^B)^{-1}$
is ascent-compatible.
$(D_I^B)^{-1}$
is ascent-compatible.
Fix
![]() $1\leq i\leq n$
. Let
$1\leq i\leq n$
. Let
![]() $\sigma $
be the element of
$\sigma $
be the element of
![]() $B_n$
such that
$B_n$
such that
![]() $\sigma (j)=-j$
for
$\sigma (j)=-j$
for
![]() $1\leq j\leq i-1$
and
$1\leq j\leq i-1$
and
![]() $\sigma (k)=k-i-n$
for
$\sigma (k)=k-i-n$
for
![]() $i\leq k\leq n$
. Let
$i\leq k\leq n$
. Let
![]() $\tau $
be the element of
$\tau $
be the element of
![]() $B_n$
such that
$B_n$
such that
![]() $\tau (j)=i-j$
for
$\tau (j)=i-j$
for
![]() $1\leq j\leq i-1$
and
$1\leq j\leq i-1$
and
![]() $\tau (k)=k$
for
$\tau (k)=k$
for
![]() $i\leq k\leq n$
. It is straightforward to check that
$i\leq k\leq n$
. It is straightforward to check that
![]() $(L_i^B)^{-1}$
is equal to the interval
$(L_i^B)^{-1}$
is equal to the interval
![]() $[\sigma ,\tau ]_{{\mathsf {L}}}$
in the left weak order. According to Theorem 3.3,
$[\sigma ,\tau ]_{{\mathsf {L}}}$
in the left weak order. According to Theorem 3.3,
![]() $(L_i^B)^{-1}$
is ascent-compatible.
$(L_i^B)^{-1}$
is ascent-compatible.
We note that
![]() $D_I^B$
and
$D_I^B$
and
![]() $L_i^B$
themselves are subsets of left descent classes, so they are ascent-compatible by Proposition 3.2. Therefore, the functions
$L_i^B$
themselves are subsets of left descent classes, so they are ascent-compatible by Proposition 3.2. Therefore, the functions
![]() $\mathcal {Q}(D_I^{B})^{-1}$
and
$\mathcal {Q}(D_I^{B})^{-1}$
and
![]() $\mathcal {Q}(L_i^B)^{-1}$
are also quasisymmetric characteristics of
$\mathcal {Q}(L_i^B)^{-1}$
are also quasisymmetric characteristics of
![]() $H_n^B(0)$
-modules by Theorems 3.1 and 3.5.
$H_n^B(0)$
-modules by Theorems 3.1 and 3.5.
Another subset of
![]() $B_n$
considered in [Reference Mayorova and Vassilieva11] is the
$B_n$
considered in [Reference Mayorova and Vassilieva11] is the ![]() associated with a standard domino tableau T. This is the set
associated with a standard domino tableau T. This is the set
![]() $C_T^B$
of all
$C_T^B$
of all
![]() $\sigma \in B_n$
that insert to T under a certain type-B analog of the Robinson–Schensted correspondence (see Section 4 for the definition of a standard domino tableau). The set
$\sigma \in B_n$
that insert to T under a certain type-B analog of the Robinson–Schensted correspondence (see Section 4 for the definition of a standard domino tableau). The set
![]() $(C_T^B)^{-1}$
is not in general ascent-compatible. However,
$(C_T^B)^{-1}$
is not in general ascent-compatible. However,
![]() $C_T^B$
itself is a subset of a left-descent class, so it is ascent-compatible, and the functions
$C_T^B$
itself is a subset of a left-descent class, so it is ascent-compatible, and the functions
![]() $\mathcal {Q}((C_T^B)^{-1})$
are quasisymmetric characteristics of
$\mathcal {Q}((C_T^B)^{-1})$
are quasisymmetric characteristics of
![]() $H_n^B(0)$
-modules.
$H_n^B(0)$
-modules.
The final example considered in [Reference Mayorova and Vassilieva11] concerns the signed arc permutations in
![]() $B_n$
. The set of signed arc permutations is ascent-compatible (although the set of their inverses is not); this ascent-compatibility is noteworthy because the set of signed arc permutations in
$B_n$
. The set of signed arc permutations is ascent-compatible (although the set of their inverses is not); this ascent-compatibility is noteworthy because the set of signed arc permutations in
![]() $B_n$
is not convex in the left weak order, so its ascent-compatibility does not follow from Theorem 3.3.
$B_n$
is not convex in the left weak order, so its ascent-compatibility does not follow from Theorem 3.3.
Let
![]() $-[n]=\{-1,\ldots ,-n\}$
. It will be convenient to represent negative numbers using overlines; for example, we will write
$-[n]=\{-1,\ldots ,-n\}$
. It will be convenient to represent negative numbers using overlines; for example, we will write ![]() instead of
instead of
![]() $-3$
. The
$-3$
. The ![]() of a signed permutation
of a signed permutation
![]() $\sigma \in B_n$
is the word
$\sigma \in B_n$
is the word
![]() $\sigma (1)\dots \sigma (n)$
. Suppose
$\sigma (1)\dots \sigma (n)$
. Suppose
![]() $x_0$
and
$x_0$
and
![]() $x_1$
are finite words that use disjoint sets of letters. A
$x_1$
are finite words that use disjoint sets of letters. A ![]() of
of
![]() $x_0$
and
$x_0$
and
![]() $x_1$
is a word w such that for each
$x_1$
is a word w such that for each
![]() $i\in \{0,1\}$
, deleting the letters in w that appear in
$i\in \{0,1\}$
, deleting the letters in w that appear in
![]() $x_{1-i}$
yields the word
$x_{1-i}$
yields the word
![]() $x_i$
. Let
$x_i$
. Let ![]() denote the set of all shuffles of
denote the set of all shuffles of
![]() $x_0$
and
$x_0$
and
![]() $x_1$
. For example, the elements of
$x_1$
. For example, the elements of ![]() are
are
A ![]() is an element of
is an element of
![]() $B_n$
whose one-line notation is a shuffle of a word
$B_n$
whose one-line notation is a shuffle of a word
![]() $a_1\dots a_p$
over the alphabet
$a_1\dots a_p$
over the alphabet
![]() $[n]$
and a word
$[n]$
and a word
![]() $b_1\dots b_{n-p}$
over the alphabet
$b_1\dots b_{n-p}$
over the alphabet
![]() $-[n]$
satisfying the following conditions:
$-[n]$
satisfying the following conditions:
-
•
 $a_{i+1}\equiv a_i+1\ \pmod n$
for all
$a_{i+1}\equiv a_i+1\ \pmod n$
for all
 $1\leq i\leq p-1$
;
$1\leq i\leq p-1$
; -
•
 $b_{j+1}\equiv b_j+1\ \pmod n$
for all
$b_{j+1}\equiv b_j+1\ \pmod n$
for all
 $1\leq j\leq n-p-1$
;
$1\leq j\leq n-p-1$
; -
•
 $a_1\equiv -b_1+1\ \, \pmod n$
if p and
$a_1\equiv -b_1+1\ \, \pmod n$
if p and
 $n-p$
are both nonzero.
$n-p$
are both nonzero.
Let
![]() $\mathcal A_n^B$
be the set of signed arc permutations in
$\mathcal A_n^B$
be the set of signed arc permutations in
![]() $B_n$
. For example,
$B_n$
. For example,

Theorem 3.7 The set
![]() $\mathcal A_n^B$
is ascent-compatible. Therefore,
$\mathcal A_n^B$
is ascent-compatible. Therefore,
![]() $\mathbb C\mathcal A_n^B$
is an
$\mathbb C\mathcal A_n^B$
is an
![]() $H_n^B(0)$
-module, and
$H_n^B(0)$
-module, and
Proof The proof is easy if
![]() $n\leq 2$
, so assume
$n\leq 2$
, so assume
![]() $n\geq 3$
. Let u and v be signed arc permutations in
$n\geq 3$
. Let u and v be signed arc permutations in
![]() $B_n$
, and suppose
$B_n$
, and suppose
![]() $s,t\in S$
are such that
$s,t\in S$
are such that
![]() $(u,v,s,t)$
is aligned. We must show that
$(u,v,s,t)$
is aligned. We must show that
![]() $su\in \mathcal A_n^B$
if and only if
$su\in \mathcal A_n^B$
if and only if
![]() $tv\in \mathcal A_n^B$
.
$tv\in \mathcal A_n^B$
.
None of the simple generators of
![]() $B_n$
other than
$B_n$
other than
![]() $s_0$
are conjugate to
$s_0$
are conjugate to
![]() $s_0$
. Since
$s_0$
. Since
![]() $u^{-1}su=v^{-1}tv$
, we have
$u^{-1}su=v^{-1}tv$
, we have
![]() $s=s_0$
if and only if
$s=s_0$
if and only if
![]() $t=s_0$
. If
$t=s_0$
. If
![]() $s=t=s_0$
, then the reflection
$s=t=s_0$
, then the reflection
![]() $u^{-1}su=v^{-1}tv$
is a transposition of the form
$u^{-1}su=v^{-1}tv$
is a transposition of the form ![]() for some
for some
![]() $k\in [n]$
. On the other hand, if s and t are not
$k\in [n]$
. On the other hand, if s and t are not
![]() $s_0$
, then the reflection
$s_0$
, then the reflection
![]() $u^{-1}su=v^{-1}tv$
can be written as
$u^{-1}su=v^{-1}tv$
can be written as ![]() for some
for some
![]() $m_1,m_2\in \pm [n]$
. We now consider four cases.
$m_1,m_2\in \pm [n]$
. We now consider four cases.
Case 1. Suppose that
![]() $s=s_0$
and that the reflection
$s=s_0$
and that the reflection
![]() $u^{-1}su=v^{-1}tv$
is either
$u^{-1}su=v^{-1}tv$
is either ![]() or
or ![]() . We consider only the case when this reflection is
. We consider only the case when this reflection is ![]() ; the other case is similar. Because
; the other case is similar. Because
![]() $s_0$
is an ascent of u, we have
$s_0$
is an ascent of u, we have ![]() and
and
![]() $(su)(1)=1$
. There exists
$(su)(1)=1$
. There exists
![]() $q\in [n]$
such that
$q\in [n]$
such that ![]() and
and ![]() . It follows that
. It follows that
![]() ${su=s_0u\in \mathcal A_n^B}$
. A similar argument shows that
${su=s_0u\in \mathcal A_n^B}$
. A similar argument shows that
![]() $tv=s_0v\in \mathcal A_n^B$
as well.
$tv=s_0v\in \mathcal A_n^B$
as well.
Case 2. Suppose that
![]() $s=s_0$
and that
$s=s_0$
and that ![]() for some
for some
![]() $2\leq k\leq n-1$
. We will show that
$2\leq k\leq n-1$
. We will show that
![]() $su,tv\not \in \mathcal A_n^B$
. Let us prove that
$su,tv\not \in \mathcal A_n^B$
. Let us prove that
![]() $su\not \in \mathcal A_n^B$
; the same argument can be used to prove that
$su\not \in \mathcal A_n^B$
; the same argument can be used to prove that
![]() $tv\not \in \mathcal A_n^B$
. Let us write u as a shuffle of a word
$tv\not \in \mathcal A_n^B$
. Let us write u as a shuffle of a word
![]() $a_1\dots a_p$
over
$a_1\dots a_p$
over
![]() $[n]$
and a word
$[n]$
and a word
![]() $b_1\dots b_{n-p}$
over
$b_1\dots b_{n-p}$
over
![]() $-[n]$
as in the definition of signed arc permutations. Because
$-[n]$
as in the definition of signed arc permutations. Because
![]() $s_0$
is an ascent of u, we have
$s_0$
is an ascent of u, we have ![]() for some
for some
![]() $1\leq j\leq n-p$
. Suppose by way of contradiction that
$1\leq j\leq n-p$
. Suppose by way of contradiction that
![]() $su\in \mathcal A_n^B$
. The one-line notation of
$su\in \mathcal A_n^B$
. The one-line notation of
![]() $su$
is obtained from that of u by changing
$su$
is obtained from that of u by changing ![]() into
into
![]() $1$
. We claim that negative entries cannot appear in the one-line notation of u (equivalently,
$1$
. We claim that negative entries cannot appear in the one-line notation of u (equivalently,
![]() $su$
) on both sides of position k; indeed, if there were negative entries on both sides of position k, then deleting the positive entries from the one-line notation of
$su$
) on both sides of position k; indeed, if there were negative entries on both sides of position k, then deleting the positive entries from the one-line notation of
![]() $su$
would result in a word over
$su$
would result in a word over
![]() $-[n]$
in which
$-[n]$
in which ![]() and
and ![]() appear consecutively, contradicting the definition of
appear consecutively, contradicting the definition of
![]() $\mathcal A_n^B$
. Similarly, positive entries cannot appear in the one-line notation of u (equivalently,
$\mathcal A_n^B$
. Similarly, positive entries cannot appear in the one-line notation of u (equivalently,
![]() $su$
) on both sides of position k. It follows that j is
$su$
) on both sides of position k. It follows that j is
![]() $1$
or
$1$
or
![]() $n-p$
. We will assume that
$n-p$
. We will assume that
![]() $j=1$
; the argument is similar if
$j=1$
; the argument is similar if
![]() $j=n-p$
. Thus, the one-line notation of u is
$j=n-p$
. Thus, the one-line notation of u is ![]() , while the one-line notation of
, while the one-line notation of
![]() $su$
is
$su$
is
![]() $a_1\dots a_p1b_2\dots b_{n-p}$
. The defining conditions of signed arc permutations then imply that
$a_1\dots a_p1b_2\dots b_{n-p}$
. The defining conditions of signed arc permutations then imply that
![]() $a_p=n$
and
$a_p=n$
and ![]() , which is impossible.
, which is impossible.
Case 3. Suppose that s and t are not
![]() $s_0$
and that
$s_0$
and that ![]() , where the set
, where the set ![]() is not equal to
is not equal to ![]() . Without loss of generality, we may assume that
. Without loss of generality, we may assume that
![]() $m_1$
is the smallest positive element of
$m_1$
is the smallest positive element of ![]() . Then
. Then
![]() $1\leq m_1\leq n-2$
. In this case, we will show that
$1\leq m_1\leq n-2$
. In this case, we will show that
![]() $su$
and
$su$
and
![]() $tv$
are not in
$tv$
are not in
![]() $\mathcal A_n^B$
. Let us prove that
$\mathcal A_n^B$
. Let us prove that
![]() $su\not \in \mathcal A_n^B$
; the same argument can be used to prove that
$su\not \in \mathcal A_n^B$
; the same argument can be used to prove that
![]() $tv\not \in \mathcal A_n^B$
. Let
$tv\not \in \mathcal A_n^B$
. Let
![]() $s=s_i$
. Let us say a q-element set
$s=s_i$
. Let us say a q-element set
![]() $J\subseteq \mathbb Z$
is a
$J\subseteq \mathbb Z$
is a ![]() modulo n if there is a set of q consecutive integers that are congruent modulo n to the elements of J. Observe that if
modulo n if there is a set of q consecutive integers that are congruent modulo n to the elements of J. Observe that if
![]() $\sigma \in \mathcal A_n^B$
, then for each
$\sigma \in \mathcal A_n^B$
, then for each
![]() $q\in [n]$
, the set
$q\in [n]$
, the set
![]() $\{|\sigma (j)|:1\leq j\leq q\}$
is a cyclic interval modulo n. Now,
$\{|\sigma (j)|:1\leq j\leq q\}$
is a cyclic interval modulo n. Now,
Since
![]() $m_1\leq n-2$
, this implies that the sets
$m_1\leq n-2$
, this implies that the sets
![]() $\{|u(j)|:1\leq j\leq m_1\}$
and
$\{|u(j)|:1\leq j\leq m_1\}$
and
![]() $\{|(su)(j)|:1\leq j\leq m_1\}$
cannot both be cyclic intervals modulo n. Since
$\{|(su)(j)|:1\leq j\leq m_1\}$
cannot both be cyclic intervals modulo n. Since
![]() $u\in \mathcal A_n^B$
, we must have
$u\in \mathcal A_n^B$
, we must have
![]() $su\not \in \mathcal A_n^B$
.
$su\not \in \mathcal A_n^B$
.
Case 4. Suppose that s and t are not
![]() $s_0$
and that
$s_0$
and that ![]() , where
, where ![]() . We will show that
. We will show that
![]() $su$
and
$su$
and
![]() $tv$
are not in
$tv$
are not in
![]() $\mathcal A_n^B$
. Let us prove that
$\mathcal A_n^B$
. Let us prove that
![]() $su\not \in \mathcal A_n^B$
; the same argument can be used to prove that
$su\not \in \mathcal A_n^B$
; the same argument can be used to prove that
![]() $tv\not \in \mathcal A_n^B$
. Let us write u as a shuffle of a word
$tv\not \in \mathcal A_n^B$
. Let us write u as a shuffle of a word
![]() $a_1\dots a_p$
over
$a_1\dots a_p$
over
![]() $[n]$
and a word
$[n]$
and a word
![]() $b_1\dots b_{n-p}$
over
$b_1\dots b_{n-p}$
over
![]() $-[n]$
as in the definition of signed arc permutations. Let
$-[n]$
as in the definition of signed arc permutations. Let
![]() $s=s_i$
. Because
$s=s_i$
. Because
![]() $s_i$
is an ascent of u, the pair
$s_i$
is an ascent of u, the pair
![]() $(u(n-1),u(n))$
must be
$(u(n-1),u(n))$
must be
![]() $(i,i+1)$
,
$(i,i+1)$
, ![]() ,
, ![]() , or
, or ![]() . Suppose first that this pair is
. Suppose first that this pair is ![]() or
or ![]() . Then,
. Then,
![]() $a_p=i+1$
and
$a_p=i+1$
and ![]() . If
. If
![]() $p\geq 2$
, then
$p\geq 2$
, then
![]() $a_{p-1}=a_p-1=i$
; if
$a_{p-1}=a_p-1=i$
; if
![]() $p=1$
, then
$p=1$
, then ![]() . In either case, we obtain a contradiction because i and
. In either case, we obtain a contradiction because i and ![]() do not appear in the one-line notation of u. Thus, we may assume that the pair
do not appear in the one-line notation of u. Thus, we may assume that the pair
![]() $(u(n-1),u(n))$
is either
$(u(n-1),u(n))$
is either
![]() $(i,i+1)$
or
$(i,i+1)$
or ![]() . If
. If
![]() $(u(n-1),u(n))=(i,i+1)$
, then the last two entries in the one-line notation of
$(u(n-1),u(n))=(i,i+1)$
, then the last two entries in the one-line notation of
![]() $su$
are
$su$
are
![]() $i+1,i$
, so it follows from the first bulleted item in the definition of a signed arc permutation that
$i+1,i$
, so it follows from the first bulleted item in the definition of a signed arc permutation that
![]() $su\not \in \mathcal A_n^B$
. Similarly, if
$su\not \in \mathcal A_n^B$
. Similarly, if ![]() , then the last two entries in the one-line notation of
, then the last two entries in the one-line notation of
![]() $su$
are
$su$
are ![]() , so it follows from the second bulleted item that
, so it follows from the second bulleted item that
![]() $su\not \in \mathcal A_n^B$
.
$su\not \in \mathcal A_n^B$
.
Remark 3.8 It could be interesting to see if some of our work on ascent-compatible sets could extend to other complex reflection groups. This could lead to connections with the generalizations of peak algebras studied in [Reference Bergeron and Hohlweg4, Reference Novelli, Saliola and Thibon14].
4 Domino tableaux and type-B peak functions
A central motivation for studying the families of functions considered in Section 3 is the fact that they expand positively into type-B analogues of Schur functions known as domino functions, which have formulas in terms of domino tableaux [Reference Mayorova and Vassilieva11]. In this section, we define an action of the type-B
![]() $0$
-Hecke algebra on standard domino tableaux, thereby obtaining a representation–theoretic interpretation of the domino functions. We then consider the shifted domino tableaux introduced by Chemli [Reference Chemli6], define a modification of these that allows
$0$
-Hecke algebra on standard domino tableaux, thereby obtaining a representation–theoretic interpretation of the domino functions. We then consider the shifted domino tableaux introduced by Chemli [Reference Chemli6], define a modification of these that allows
![]() $0$
entries, and introduce standard shifted domino tableaux. We show that the generating functions of the (modified) shifted domino tableaux, which we call shifted domino functions, expand positively in the type-B peak functions, with the expansion indexed by standard shifted domino tableaux. Similarly to how domino functions form a type-B analogue of Schur functions, the shifted domino functions may be regarded as forming a type-B analogue of Schur Q-functions.
$0$
entries, and introduce standard shifted domino tableaux. We show that the generating functions of the (modified) shifted domino tableaux, which we call shifted domino functions, expand positively in the type-B peak functions, with the expansion indexed by standard shifted domino tableaux. Similarly to how domino functions form a type-B analogue of Schur functions, the shifted domino functions may be regarded as forming a type-B analogue of Schur Q-functions.
4.1 Standard domino tableaux
Let
![]() $\lambda $
be a partition. A
$\lambda $
be a partition. A ![]() of
of
![]() $\lambda $
is a tiling of the Young diagram of shape
$\lambda $
is a tiling of the Young diagram of shape
![]() $\lambda $
by
$\lambda $
by
![]() $1\times 2$
and
$1\times 2$
and
![]() $2\times 1$
rectangles called
$2\times 1$
rectangles called ![]() . The partition
. The partition
![]() $\lambda $
is called
$\lambda $
is called ![]() if a domino tiling of
if a domino tiling of
![]() $\lambda $
exists. For
$\lambda $
exists. For
![]() $\lambda $
a pavable partition of
$\lambda $
a pavable partition of
![]() $2n$
, a
$2n$
, a ![]() of shape
of shape
![]() $\lambda $
is a bijective filling of a domino tiling of
$\lambda $
is a bijective filling of a domino tiling of
![]() $\lambda $
with entries from
$\lambda $
with entries from
![]() $[n]$
such that entries increase from left to right along rows and from top to bottom in columns (see Figure 1). Let
$[n]$
such that entries increase from left to right along rows and from top to bottom in columns (see Figure 1). Let
![]() $\mathsf {SDT}(\lambda )$
denote the set of standard domino tableaux of shape
$\mathsf {SDT}(\lambda )$
denote the set of standard domino tableaux of shape
![]() $\lambda $
.
$\lambda $
.
Figure 1: A standard domino tableau of shape
![]() $(5,4,4,1)\vdash 14$
.
$(5,4,4,1)\vdash 14$
.
Suppose
![]() $T\in \mathsf {SDT}(\lambda )$
. Let
$T\in \mathsf {SDT}(\lambda )$
. Let
![]() $\mathrm {dom}_i(T)$
denote the domino in T filled with the entry i. A number
$\mathrm {dom}_i(T)$
denote the domino in T filled with the entry i. A number
![]() $i\in [0,n-1]$
is a
$i\in [0,n-1]$
is a ![]() of T if
of T if
![]() $i=0$
and
$i=0$
and
![]() $\mathrm {dom}_1(T)$
is vertical or if
$\mathrm {dom}_1(T)$
is vertical or if
![]() $i>0$
and
$i>0$
and
![]() $\mathrm {dom}_{i+1}(T)$
is strictly lower than
$\mathrm {dom}_{i+1}(T)$
is strictly lower than
![]() $\mathrm {dom}_i(T)$
. Let
$\mathrm {dom}_i(T)$
. Let
![]() $\mathrm {Des}(T)$
be the set of descents of T. For example, the descent set of the domino tableau in Figure 1 is
$\mathrm {Des}(T)$
be the set of descents of T. For example, the descent set of the domino tableau in Figure 1 is
![]() $\{0,2,5,6\}$
. The
$\{0,2,5,6\}$
. The ![]()
![]() $G_\lambda $
[Reference Mayorova and Vassilieva11] is defined by
$G_\lambda $
[Reference Mayorova and Vassilieva11] is defined by
For
![]() $1\le i \le n-1$
, let
$1\le i \le n-1$
, let
![]() $s_i(T)$
be the tableau obtained by exchanging the entries i and
$s_i(T)$
be the tableau obtained by exchanging the entries i and
![]() $i+1$
. If
$i+1$
. If
![]() $\mathrm {dom}_1(T)$
and
$\mathrm {dom}_1(T)$
and
![]() $\mathrm {dom}_2(T)$
tile the northwest-most
$\mathrm {dom}_2(T)$
tile the northwest-most
![]() $2\times 2$
square in T, then we let
$2\times 2$
square in T, then we let
![]() $s_0(T)$
be the tableau obtained by switching the orientation of both these dominoes (i.e., from horizontal to vertical or vice versa); otherwise, we say
$s_0(T)$
be the tableau obtained by switching the orientation of both these dominoes (i.e., from horizontal to vertical or vice versa); otherwise, we say
![]() $s_0(T)$
is not defined (in particular, we would say
$s_0(T)$
is not defined (in particular, we would say
![]() $s_0(T)\not \in \mathsf {SDT}(\lambda )$
in this case). If
$s_0(T)\not \in \mathsf {SDT}(\lambda )$
in this case). If
![]() $s_0(T)$
is defined and
$s_0(T)$
is defined and
![]() $1$
appears above (respectively, left of)
$1$
appears above (respectively, left of)
![]() $2$
in T, then we place
$2$
in T, then we place
![]() $1$
left of (respectively, above)
$1$
left of (respectively, above)
![]() $2$
in
$2$
in
![]() $s_0(T)$
. We define operators
$s_0(T)$
. We define operators
![]() $\pi _0, \pi _1, \ldots \pi _{n-1}$
on
$\pi _0, \pi _1, \ldots \pi _{n-1}$
on
![]() $\mathbb C\mathsf {SDT}(\lambda )$
(the complex vector space with basis
$\mathbb C\mathsf {SDT}(\lambda )$
(the complex vector space with basis
![]() $\mathsf {SDT}(\lambda )$
) by
$\mathsf {SDT}(\lambda )$
) by
 $$\begin{align*}\pi_i(T) = \begin{cases} -T & \mbox{ if } i\in\mathrm{Des}(T) \\ 0 & \mbox{ if } i\notin\mathrm{Des}(T)\mbox{ and }s_i(T)\notin\mathsf{SDT}(\lambda) \\ s_i(T) & \mbox{ if } i\notin\mathrm{Des}(T)\mbox{ and }s_i(T)\in\mathsf{SDT}(\lambda). \end{cases}\end{align*}$$
$$\begin{align*}\pi_i(T) = \begin{cases} -T & \mbox{ if } i\in\mathrm{Des}(T) \\ 0 & \mbox{ if } i\notin\mathrm{Des}(T)\mbox{ and }s_i(T)\notin\mathsf{SDT}(\lambda) \\ s_i(T) & \mbox{ if } i\notin\mathrm{Des}(T)\mbox{ and }s_i(T)\in\mathsf{SDT}(\lambda). \end{cases}\end{align*}$$
Example 4.1 Let
![]() $\lambda =(4,3,3)$
and
$\lambda =(4,3,3)$
and

Then, we have

We also have
![]() $\pi _1(T)=\pi _3(T)=-T$
and
$\pi _1(T)=\pi _3(T)=-T$
and
![]() $\pi _4(T)=0$
.
$\pi _4(T)=0$
.
Theorem 4.2 Let
![]() $\lambda $
be a pavable partition of
$\lambda $
be a pavable partition of
![]() $2n$
. The operators
$2n$
. The operators
![]() $\pi _0, \pi _1, \ldots , \pi _{n-1}$
define an action of
$\pi _0, \pi _1, \ldots , \pi _{n-1}$
define an action of
![]() $H_n^B(0)$
on
$H_n^B(0)$
on
![]() $\mathbb C\mathsf {SDT}(\lambda )$
.
$\mathbb C\mathsf {SDT}(\lambda )$
.
Proof We need to demonstrate that
![]() $\pi _0, \pi _1, \ldots , \pi _{n-1}$
satisfy the type-B
$\pi _0, \pi _1, \ldots , \pi _{n-1}$
satisfy the type-B
![]() $0$
-Hecke relations. Fix
$0$
-Hecke relations. Fix
![]() $T\in \mathsf {SDT}(\lambda )$
. First, we show that
$T\in \mathsf {SDT}(\lambda )$
. First, we show that
![]() $\pi _i^2(T)=-\pi _i(T)$
. This is immediate if
$\pi _i^2(T)=-\pi _i(T)$
. This is immediate if
![]() $\pi _i(T)=0$
or
$\pi _i(T)=0$
or
![]() $\pi _i(T)=-T$
. If
$\pi _i(T)=-T$
. If
![]() $\pi _i(T)=s_i(T)$
, then i is a descent of
$\pi _i(T)=s_i(T)$
, then i is a descent of
![]() $s_i(T)$
, so
$s_i(T)$
, so
![]() $\pi _i^2(T) = -s_i(T)=-\pi _i(T)$
.
$\pi _i^2(T) = -s_i(T)=-\pi _i(T)$
.
Next, we show that
![]() $\pi _i\pi _j(T) = \pi _j\pi _i(T)$
whenever
$\pi _i\pi _j(T) = \pi _j\pi _i(T)$
whenever
![]() $j-i\geq 2$
. If
$j-i\geq 2$
. If
![]() $i,j\geq 1$
, then this is immediate since the action of
$i,j\geq 1$
, then this is immediate since the action of
![]() $\pi _i$
only affects the dominoes with entries i and
$\pi _i$
only affects the dominoes with entries i and
![]() $i+1$
while the action of
$i+1$
while the action of
![]() $\pi _j$
only affects the dominoes with entries j and
$\pi _j$
only affects the dominoes with entries j and
![]() $j+1$
. A similar argument handles the case when
$j+1$
. A similar argument handles the case when
![]() $i=0$
and
$i=0$
and
![]() $j\geq 3$
since the action of
$j\geq 3$
since the action of
![]() $\pi _0$
can only affect the dominoes with entries
$\pi _0$
can only affect the dominoes with entries
![]() $1$
and
$1$
and
![]() $2$
. Now suppose
$2$
. Now suppose
![]() $i=0$
and
$i=0$
and
![]() $j=2$
; we need to show that
$j=2$
; we need to show that
![]() $\pi _0\pi _2(T) = \pi _2\pi _0(T)$
. If
$\pi _0\pi _2(T) = \pi _2\pi _0(T)$
. If
![]() $\mathrm {dom}_1(T)$
is vertical, then
$\mathrm {dom}_1(T)$
is vertical, then
![]() $\pi _0(T)=-T$
, so we need to check that
$\pi _0(T)=-T$
, so we need to check that
![]() $\pi _0\pi _2(T)=-\pi _2(T)$
. This is immediate if
$\pi _0\pi _2(T)=-\pi _2(T)$
. This is immediate if
![]() $\pi _2(T)=0$
. If
$\pi _2(T)=0$
. If
![]() $\pi _2(T)\neq 0$
, then there is a unique tableau
$\pi _2(T)\neq 0$
, then there is a unique tableau
![]() $T'$
in the support of
$T'$
in the support of
![]() $\pi _2(T)$
, and
$\pi _2(T)$
, and
![]() $\mathrm {dom}_1(T')$
is vertical. In this case,
$\mathrm {dom}_1(T')$
is vertical. In this case,
![]() $\pi _0(T')=-T'$
, so the desired identity follows. Now assume
$\pi _0(T')=-T'$
, so the desired identity follows. Now assume
![]() $\mathrm {dom}_1(T)$
is horizontal. If there is not a horizontal domino immediately below
$\mathrm {dom}_1(T)$
is horizontal. If there is not a horizontal domino immediately below
![]() $\mathrm {dom}_1(T)$
in T, then it is straightforward to check that
$\mathrm {dom}_1(T)$
in T, then it is straightforward to check that
![]() $\pi _0\pi _2(T)$
and
$\pi _0\pi _2(T)$
and
![]() $\pi _2\pi _0(T)$
are both
$\pi _2\pi _0(T)$
are both
![]() $0$
. Thus, we may assume that the northwest-most
$0$
. Thus, we may assume that the northwest-most
![]() $2\times 2$
square in T is tiled by two horizontal dominoes. There are six remaining cases that depend on the relative positions of the entries
$2\times 2$
square in T is tiled by two horizontal dominoes. There are six remaining cases that depend on the relative positions of the entries
![]() $1,2,3$
in T; we can check them by hand as follows:
$1,2,3$
in T; we can check them by hand as follows:


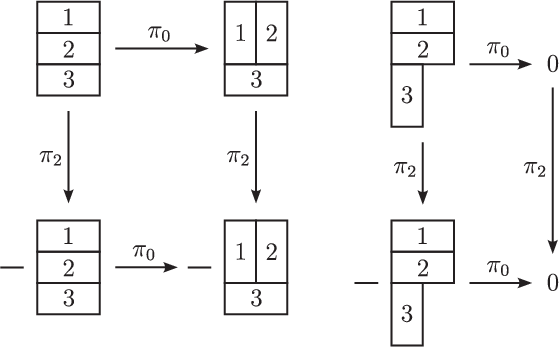
We next prove that
![]() $\pi _0\pi _1\pi _0\pi _1(T) = \pi _1\pi _0\pi _1\pi _0(T)$
. The actions of
$\pi _0\pi _1\pi _0\pi _1(T) = \pi _1\pi _0\pi _1\pi _0(T)$
. The actions of
![]() $\pi _0$
and
$\pi _0$
and
![]() $\pi _1$
on T depend only on the positions of
$\pi _1$
on T depend only on the positions of
![]() $\mathrm {dom}_1(T)$
and
$\mathrm {dom}_1(T)$
and
![]() $\mathrm {dom}_2(T)$
. By the definition of domino tableaux, we cannot have
$\mathrm {dom}_2(T)$
. By the definition of domino tableaux, we cannot have
![]() $\pi _1(T)=s_1(T)$
, so
$\pi _1(T)=s_1(T)$
, so
![]() $\pi _0\pi _1\pi _0\pi _1(T)$
is either
$\pi _0\pi _1\pi _0\pi _1(T)$
is either
![]() $-\pi _0\pi _1\pi _0(T)$
or
$-\pi _0\pi _1\pi _0(T)$
or
![]() $0$
. If
$0$
. If
![]() $\pi _0(T)=0$
, then both
$\pi _0(T)=0$
, then both
![]() $\pi _1\pi _0\pi _1\pi _0(T)$
and
$\pi _1\pi _0\pi _1\pi _0(T)$
and
![]() $\pi _0\pi _1\pi _0\pi _1(T)$
are
$\pi _0\pi _1\pi _0\pi _1(T)$
are
![]() $0$
. If
$0$
. If
![]() $\pi _0(T)=s_0(T)$
, then we have
$\pi _0(T)=s_0(T)$
, then we have
![]() $\pi _1(T)=-T$
and
$\pi _1(T)=-T$
and
![]() $\pi _1\pi _0(T)=0$
, so again both
$\pi _1\pi _0(T)=0$
, so again both
![]() $\pi _1\pi _0\pi _1\pi _0(T)$
and
$\pi _1\pi _0\pi _1\pi _0(T)$
and
![]() $\pi _0\pi _1\pi _0\pi _1(T)$
are
$\pi _0\pi _1\pi _0\pi _1(T)$
are
![]() $0$
. If
$0$
. If
![]() $\pi _0(T)=-T$
, then
$\pi _0(T)=-T$
, then
![]() $\pi _1\pi _0\pi _1\pi _0(T)$
and
$\pi _1\pi _0\pi _1\pi _0(T)$
and
![]() $\pi _0\pi _1\pi _0\pi _1(T)$
are both
$\pi _0\pi _1\pi _0\pi _1(T)$
are both
![]() $0$
if
$0$
if
![]() $\pi _1(T)=0$
and are both equal to T if
$\pi _1(T)=0$
and are both equal to T if
![]() $\pi _1(T)=-T$
.
$\pi _1(T)=-T$
.
Finally, we show that for
![]() $i\geq 1$
, we have
$i\geq 1$
, we have
![]() $\pi _i\pi _{i+1}\pi _i(T) = \pi _{i+1}\pi _i\pi _{i+1}(T)$
. We consider three cases.
$\pi _i\pi _{i+1}\pi _i(T) = \pi _{i+1}\pi _i\pi _{i+1}(T)$
. We consider three cases.
Case 1. Suppose
![]() $\pi _i(T)=0$
. In this case,
$\pi _i(T)=0$
. In this case,
![]() $\pi _i\pi _{i+1}\pi _i(T)=0$
, and it follows immediately that
$\pi _i\pi _{i+1}\pi _i(T)=0$
, and it follows immediately that
![]() ${\pi _{i+1}\pi _i\pi _{i+1}(T) = 0}$
if either
${\pi _{i+1}\pi _i\pi _{i+1}(T) = 0}$
if either
![]() $\pi _{i+1}(T)=0$
or
$\pi _{i+1}(T)=0$
or
![]() $\pi _{i+1}(T)=-T$
. Suppose
$\pi _{i+1}(T)=-T$
. Suppose
![]() $\pi _{i+1}(T) = s_{i+1}(T)$
. Then
$\pi _{i+1}(T) = s_{i+1}(T)$
. Then
![]() $\mathrm {dom}_{i+1}(T)$
shares a row with
$\mathrm {dom}_{i+1}(T)$
shares a row with
![]() $\mathrm {dom}_i(T)$
, and
$\mathrm {dom}_i(T)$
, and
![]() $\mathrm {dom}_{i+2}(T)$
is strictly above and strictly right of
$\mathrm {dom}_{i+2}(T)$
is strictly above and strictly right of
![]() $\mathrm {dom}_{i+1}(T)$
. It follows that
$\mathrm {dom}_{i+1}(T)$
. It follows that
![]() $\pi _i\pi _{i+1}(T) = s_is_{i+1}(T)$
. The dominoes occupied by i and
$\pi _i\pi _{i+1}(T) = s_is_{i+1}(T)$
. The dominoes occupied by i and
![]() $i+1$
in T are occupied by
$i+1$
in T are occupied by
![]() $i+1$
and
$i+1$
and
![]() $i+2$
, respectively, in
$i+2$
, respectively, in
![]() $s_is_{i+1}(T)$
, so
$s_is_{i+1}(T)$
, so
![]() $\pi _{i+1}\pi _i\pi _{i+1}(T) = \pi _{i+1}s_is_{i+1}(T) = 0$
.
$\pi _{i+1}\pi _i\pi _{i+1}(T) = \pi _{i+1}s_is_{i+1}(T) = 0$
.
Case 2. Suppose
![]() $\pi _i(T)=-T$
. If
$\pi _i(T)=-T$
. If
![]() $\pi _{i+1}(T)=0$
, then
$\pi _{i+1}(T)=0$
, then
![]() $\pi _{i}\pi _{i+1}\pi _{i}(T)$
and
$\pi _{i}\pi _{i+1}\pi _{i}(T)$
and
![]() $\pi _{i+1}\pi _{i}\pi _{i+1}(T)$
are both
$\pi _{i+1}\pi _{i}\pi _{i+1}(T)$
are both
![]() $0$
. If
$0$
. If
![]() $\pi _{i+1}(T)=-T$
, then
$\pi _{i+1}(T)=-T$
, then
![]() $\pi _{i}\pi _{i+1}\pi _{i}(T)$
and
$\pi _{i}\pi _{i+1}\pi _{i}(T)$
and
![]() $\pi _{i+1}\pi _{i}\pi _{i+1}(T)$
are both equal to
$\pi _{i+1}\pi _{i}\pi _{i+1}(T)$
are both equal to
![]() $-T$
. Now assume that
$-T$
. Now assume that
![]() $\pi _{i+1}(T)=s_{i+1}(T)$
. Let
$\pi _{i+1}(T)=s_{i+1}(T)$
. Let
![]() $X=\pi _i(s_{i+1}(T))$
. Since
$X=\pi _i(s_{i+1}(T))$
. Since
![]() $\pi _{i}\pi _{i+1}\pi _{i}(T)=-X$
and
$\pi _{i}\pi _{i+1}\pi _{i}(T)=-X$
and
![]() ${\pi _{i+1}\pi _{i}\pi _{i+1}(T)=\pi _{i+1}(X)}$
, we need to show that
${\pi _{i+1}\pi _{i}\pi _{i+1}(T)=\pi _{i+1}(X)}$
, we need to show that
![]() $\pi _{i+1}(X)=-X$
. This is obvious if
$\pi _{i+1}(X)=-X$
. This is obvious if
![]() $X=0$
. If
$X=0$
. If
![]() $X=s_is_{i+1}(T)$
, then we have
$X=s_is_{i+1}(T)$
, then we have
![]() $\mathrm {dom}_i(T)=\mathrm {dom}_{i+1}(X)$
and
$\mathrm {dom}_i(T)=\mathrm {dom}_{i+1}(X)$
and
![]() $\mathrm {dom}_{i+1}(T)=\mathrm {dom}_{i+2}(X)$
, so
$\mathrm {dom}_{i+1}(T)=\mathrm {dom}_{i+2}(X)$
, so
![]() $i+1\in \mathrm {Des}(X)$
(since
$i+1\in \mathrm {Des}(X)$
(since
![]() $i\in \mathrm {Des}(T)$
). In this case,
$i\in \mathrm {Des}(T)$
). In this case,
![]() $\pi _{i+1}(X)=-X$
, as desired. Finally, suppose
$\pi _{i+1}(X)=-X$
, as desired. Finally, suppose
![]() $X=-s_{i+1}(T)$
. Because
$X=-s_{i+1}(T)$
. Because
![]() $\pi _{i+1}(T)=s_{i+1}(T)$
, it follows from the definition of the action of
$\pi _{i+1}(T)=s_{i+1}(T)$
, it follows from the definition of the action of
![]() $\pi _{i+1}$
that
$\pi _{i+1}$
that
![]() $i+1\in \mathrm {Des}(s_{i+1}(T))$
. Consequently,
$i+1\in \mathrm {Des}(s_{i+1}(T))$
. Consequently,
![]() ${\pi _{i+1}(X)=-\pi _{i+1}(s_{i+1}(T))=s_{i+1}(T)=-X}$
.
${\pi _{i+1}(X)=-\pi _{i+1}(s_{i+1}(T))=s_{i+1}(T)=-X}$
.
Case 3. Suppose
![]() $\pi _i(T)=s_i(T)$
. For this case, let us first assume
$\pi _i(T)=s_i(T)$
. For this case, let us first assume
![]() $\pi _{i+1}(T)=0$
. Then
$\pi _{i+1}(T)=0$
. Then
![]() $\mathrm {dom}_{i+1}(T)$
is strictly above
$\mathrm {dom}_{i+1}(T)$
is strictly above
![]() $\mathrm {dom}_i(T)$
but not strictly above
$\mathrm {dom}_i(T)$
but not strictly above
![]() $\mathrm {dom}_{i+2}(T)$
. It follows that
$\mathrm {dom}_{i+2}(T)$
. It follows that
![]() $\mathrm {dom}_{i+1}(s_i(T))$
is not strictly above
$\mathrm {dom}_{i+1}(s_i(T))$
is not strictly above
![]() $\mathrm {dom}_{i+2}(s_i(T))$
, so
$\mathrm {dom}_{i+2}(s_i(T))$
, so
![]() $\pi _{i+1}(s_i(T))$
is either
$\pi _{i+1}(s_i(T))$
is either
![]() $0$
or
$0$
or
![]() $s_{i+1}s_i(T)$
. If
$s_{i+1}s_i(T)$
. If
![]() $\pi _{i+1}(s_i(T))=0$
, then
$\pi _{i+1}(s_i(T))=0$
, then
![]() $\pi _{i}\pi _{i+1}\pi _{i}(T)$
and
$\pi _{i}\pi _{i+1}\pi _{i}(T)$
and
![]() $\pi _{i+1}\pi _{i}\pi _{i+1}(T)$
are both
$\pi _{i+1}\pi _{i}\pi _{i+1}(T)$
are both
![]() $0$
. On the other hand, if
$0$
. On the other hand, if
![]() $\pi _{i+1}(s_i(T))=s_{i+1}s_i(T)$
, then we have
$\pi _{i+1}(s_i(T))=s_{i+1}s_i(T)$
, then we have
![]() ${\mathrm {dom}_i(\pi _{i+1}\pi _i(T))=\mathrm {dom}_{i+1}(T)}$
and
${\mathrm {dom}_i(\pi _{i+1}\pi _i(T))=\mathrm {dom}_{i+1}(T)}$
and
![]() $\mathrm {dom}_{i+1}(\pi _{i+1}\pi _i(T))=\mathrm {dom}_{i+2}(T)$
, so the assumption that
$\mathrm {dom}_{i+1}(\pi _{i+1}\pi _i(T))=\mathrm {dom}_{i+2}(T)$
, so the assumption that
![]() $\pi _{i+1}(T)=0$
implies that
$\pi _{i+1}(T)=0$
implies that
![]() $\pi _{i}\pi _{i+1}\pi _i(T)=0=\pi _{i+1}\pi _i\pi _{i+1}(T)$
.
$\pi _{i}\pi _{i+1}\pi _i(T)=0=\pi _{i+1}\pi _i\pi _{i+1}(T)$
.
Now assume
![]() $\pi _{i+1}(T)\neq 0$
. Then,
$\pi _{i+1}(T)\neq 0$
. Then,
![]() $\pi _{i+1}(T)$
is either
$\pi _{i+1}(T)$
is either
![]() $-T$
or
$-T$
or
![]() $s_{i+1}(T)$
. These two subcases are similar, so we will only consider the subcase in which
$s_{i+1}(T)$
. These two subcases are similar, so we will only consider the subcase in which
![]() $\pi _{i+1}(T)=-T$
. This means that
$\pi _{i+1}(T)=-T$
. This means that
![]() $\mathrm {dom}_{i+1}(T)$
is strictly above both
$\mathrm {dom}_{i+1}(T)$
is strictly above both
![]() $\mathrm {dom}_{i}(T)$
and
$\mathrm {dom}_{i}(T)$
and
![]() $\mathrm {dom}_{i+2}(T)$
. Let
$\mathrm {dom}_{i+2}(T)$
. Let
![]() $X=\pi _{i+1}\pi _i(T)$
. If
$X=\pi _{i+1}\pi _i(T)$
. If
![]() $X=0$
, then
$X=0$
, then
![]() $\pi _{i}\pi _{i+1}\pi _{i}(T)$
and
$\pi _{i}\pi _{i+1}\pi _{i}(T)$
and
![]() $\pi _{i+1}\pi _{i}\pi _{i+1}(T)$
are both
$\pi _{i+1}\pi _{i}\pi _{i+1}(T)$
are both
![]() $0$
, so we may assume X is either
$0$
, so we may assume X is either
![]() $s_{i+1}s_i(T)$
or
$s_{i+1}s_i(T)$
or
![]() $-s_i(T)$
. Let
$-s_i(T)$
. Let
![]() $T'$
be the unique tableau in the support of X. We have
$T'$
be the unique tableau in the support of X. We have
![]() $\pi _i\pi _{i+1}\pi _i(T)=\pi _i(X)$
and
$\pi _i\pi _{i+1}\pi _i(T)=\pi _i(X)$
and
![]() $\pi _{i+1}\pi _i\pi _{i+1}(T)=-X$
, so we need to show that
$\pi _{i+1}\pi _i\pi _{i+1}(T)=-X$
, so we need to show that
![]() $\pi _i(X)=-X$
. Since the action of
$\pi _i(X)=-X$
. Since the action of
![]() $\pi _{i+1}$
does not affect the domino with entry i, we have
$\pi _{i+1}$
does not affect the domino with entry i, we have
![]() $\mathrm {dom}_i(T')=\mathrm {dom}_i(s_i(T))=\mathrm {dom}_{i+1}(T)$
. Because
$\mathrm {dom}_i(T')=\mathrm {dom}_i(s_i(T))=\mathrm {dom}_{i+1}(T)$
. Because
![]() $\mathrm {dom}_{i+1}(T)$
is strictly above
$\mathrm {dom}_{i+1}(T)$
is strictly above
![]() $\mathrm {dom}_{i}(T)$
and
$\mathrm {dom}_{i}(T)$
and
![]() $\mathrm {dom}_{i+2}(T)$
, we see that
$\mathrm {dom}_{i+2}(T)$
, we see that
![]() $i\in \mathrm {Des}(T')$
. It follows that
$i\in \mathrm {Des}(T')$
. It follows that
![]() $\pi _i(T')=-T'$
, so
$\pi _i(T')=-T'$
, so
![]() $\pi _i(X)=-X$
.
$\pi _i(X)=-X$
.
In what follows, we write
![]() $\mathbb C\mathsf {SDT}(\lambda )$
for the
$\mathbb C\mathsf {SDT}(\lambda )$
for the
![]() $H_n^B(0)$
-module from Theorem 4.2.
$H_n^B(0)$
-module from Theorem 4.2.
Theorem 4.3 For
![]() $\lambda $
a pavable partition, we have
$\lambda $
a pavable partition, we have
![]() $\mathrm {ch}^B(\mathbb C\mathsf {SDT}(\lambda ))=G_\lambda $
.
$\mathrm {ch}^B(\mathbb C\mathsf {SDT}(\lambda ))=G_\lambda $
.
Proof Assume that
![]() $\lambda \vdash 2n$
. For
$\lambda \vdash 2n$
. For
![]() $T,T'\in \mathsf {SDT}(\lambda )$
, let us write
$T,T'\in \mathsf {SDT}(\lambda )$
, let us write
![]() $T\preceq T'$
if there is a (possibly empty) sequence
$T\preceq T'$
if there is a (possibly empty) sequence
![]() $i_1,\ldots ,i_r$
of indices in
$i_1,\ldots ,i_r$
of indices in
![]() $[0,n-1]$
such that
$[0,n-1]$
such that
![]() $T'=\pi _{i_r}\dots \pi _{i_1}(T)$
. We claim that
$T'=\pi _{i_r}\dots \pi _{i_1}(T)$
. We claim that
![]() $\preceq $
is a partial order. It is clear that
$\preceq $
is a partial order. It is clear that
![]() $\preceq $
is reflective and transitive. It follows from the definition of the action of
$\preceq $
is reflective and transitive. It follows from the definition of the action of
![]() $\pi _0,\ldots ,\pi _{n-1}$
that if
$\pi _0,\ldots ,\pi _{n-1}$
that if
![]() $T\preceq T'$
, then
$T\preceq T'$
, then
![]() $\mathrm {Des}(T)\supseteq \mathrm {Des}(T')$
, where equality holds if and only if
$\mathrm {Des}(T)\supseteq \mathrm {Des}(T')$
, where equality holds if and only if
![]() $T=T'$
. This implies that
$T=T'$
. This implies that
![]() $\preceq $
is antisymmetric.
$\preceq $
is antisymmetric.
Let
![]() $m=|\mathsf {SDT}(\lambda )|$
, and let
$m=|\mathsf {SDT}(\lambda )|$
, and let
![]() $T_1,\ldots ,T_m$
be a linear extension of the poset
$T_1,\ldots ,T_m$
be a linear extension of the poset
![]() ${(\mathsf {SDT}(\lambda ),\preceq )}$
. For
${(\mathsf {SDT}(\lambda ),\preceq )}$
. For
![]() $0\leq k\leq m$
, let
$0\leq k\leq m$
, let
![]() $\textbf {N}_k=\text {span}\{T_1,\ldots ,T_k\}$
. Using an argument very similar to the one used in the proof of Theorem 3.5, we find that
$\textbf {N}_k=\text {span}\{T_1,\ldots ,T_k\}$
. Using an argument very similar to the one used in the proof of Theorem 3.5, we find that
![]() $\textbf {N}_k/\textbf {N}_{k-1}$
is isomorphic to the simple
$\textbf {N}_k/\textbf {N}_{k-1}$
is isomorphic to the simple
![]() $H_n^B(0)$
-module
$H_n^B(0)$
-module
![]() $\mathcal S_{\mathrm {Des}(T_k)}^B$
. We have the filtration
$\mathcal S_{\mathrm {Des}(T_k)}^B$
. We have the filtration
![]() $0= \textbf {N}_0\subseteq \textbf {N}_1\subseteq \dots \subseteq \textbf {N}_m=\mathbb C\mathsf {SDT}(\lambda )$
, so
$0= \textbf {N}_0\subseteq \textbf {N}_1\subseteq \dots \subseteq \textbf {N}_m=\mathbb C\mathsf {SDT}(\lambda )$
, so
 $$\begin{align*}\mathrm{ch}^B(\mathbb C\mathsf{SDT}(\lambda))=\sum_{k=1}^m\mathrm{ch}^B(\textbf{N}/\textbf{N}_{k-1})=\sum_{k=1}^m F_{\mathrm{Des}(T_k)}^B=G_\lambda.\\[-42pt] \end{align*}$$
$$\begin{align*}\mathrm{ch}^B(\mathbb C\mathsf{SDT}(\lambda))=\sum_{k=1}^m\mathrm{ch}^B(\textbf{N}/\textbf{N}_{k-1})=\sum_{k=1}^m F_{\mathrm{Des}(T_k)}^B=G_\lambda.\\[-42pt] \end{align*}$$
4.2 Shifted domino tableaux
A domino tiling of a pavable partition
![]() $\lambda $
is a
$\lambda $
is a ![]() of
of
![]() $\lambda $
if there is no vertical domino d lying on the main diagonal such that all dominoes left of d and adjacent to d are strictly below the main diagonal. Given a shifted tiling of
$\lambda $
if there is no vertical domino d lying on the main diagonal such that all dominoes left of d and adjacent to d are strictly below the main diagonal. Given a shifted tiling of
![]() $\lambda $
, we define a
$\lambda $
, we define a ![]() of shape
of shape
![]() $\lambda $
to be a filling of the dominoes in the tiling lying weakly above the main diagonal with entries from the totally ordered set
$\lambda $
to be a filling of the dominoes in the tiling lying weakly above the main diagonal with entries from the totally ordered set
![]() $\{0<1'<1<2'<2<\dots \}$
such that:
$\{0<1'<1<2'<2<\dots \}$
such that:
-
(1) entries weakly increase from left to right along rows and from top to bottom in columns;
-
(2) each row contains at most one
 $i'$
, and each column contains at most one i;
$i'$
, and each column contains at most one i; -
(3) the northwest-most domino may be filled with
 $0$
only if it is horizontal.
$0$
only if it is horizontal.
This definition is a modification of the one given by Chemli [Reference Chemli6], in which there are no zero entries. Denote the set of semistandard shifted domino tableaux of shape
![]() $\lambda $
by
$\lambda $
by
![]() $\mathsf {SSShDT}(\lambda )$
. For
$\mathsf {SSShDT}(\lambda )$
. For
![]() $T\in \mathsf {SSShDT}(\lambda )$
, let
$T\in \mathsf {SSShDT}(\lambda )$
, let
![]() $\mathrm {wt}(T)$
denote the
$\mathrm {wt}(T)$
denote the ![]() of T, which we define to be the vector
of T, which we define to be the vector
![]() $(\mathrm {wt}_0(T),\mathrm {wt}_1(T),\ldots )$
, where
$(\mathrm {wt}_0(T),\mathrm {wt}_1(T),\ldots )$
, where
![]() $\mathrm {wt}_i(T)$
is the number of entries in T equal to i or
$\mathrm {wt}_i(T)$
is the number of entries in T equal to i or
![]() $i'$
(in particular,
$i'$
(in particular,
![]() $\mathrm {wt}_0(T)$
is the number of
$\mathrm {wt}_0(T)$
is the number of
![]() $0$
entries in T). Let us write
$0$
entries in T). Let us write
![]() $x^{\mathrm {wt}(T)}=x_0^{\mathrm {wt}_0(T)}x_1^{\mathrm {wt}_1(T)}\dots $
. We define the
$x^{\mathrm {wt}(T)}=x_0^{\mathrm {wt}_0(T)}x_1^{\mathrm {wt}_1(T)}\dots $
. We define the ![]() indexed by
indexed by
![]() $\lambda $
to be
$\lambda $
to be
Remark 4.4 Chemli’s definition includes a further assumption on the
![]() $2$
-quotient of
$2$
-quotient of
![]() $\lambda $
, which is a certain pair of partitions obtained from
$\lambda $
, which is a certain pair of partitions obtained from
![]() $\lambda $
(see [Reference Chemli6, Section 2.3] for details). This assumption is necessary in [Reference Chemli6] in order to obtain a bijection between shifted domino tableaux and pairs of shifted Young tableaux. We do not need this assumption, and therefore our shifted domino function
$\lambda $
(see [Reference Chemli6, Section 2.3] for details). This assumption is necessary in [Reference Chemli6] in order to obtain a bijection between shifted domino tableaux and pairs of shifted Young tableaux. We do not need this assumption, and therefore our shifted domino function
![]() $H_\lambda $
is defined for any pavable partition
$H_\lambda $
is defined for any pavable partition
![]() $\lambda $
. The technical assumption regarding vertical dominoes on the main diagonal, also necessary for the bijection in [Reference Chemli6], is not needed in any of our proofs. However, we choose to retain this assumption to maintain a closer analogy between our shifted domino functions and the shifted domino tableau generating functions that are shown to be products of Schur Q-functions in [Reference Chemli6].
$\lambda $
. The technical assumption regarding vertical dominoes on the main diagonal, also necessary for the bijection in [Reference Chemli6], is not needed in any of our proofs. However, we choose to retain this assumption to maintain a closer analogy between our shifted domino functions and the shifted domino tableau generating functions that are shown to be products of Schur Q-functions in [Reference Chemli6].
Define a ![]() of shape
of shape
![]() $\lambda $
to be a bijective filling of the dominoes weakly above the main diagonal in a shifted tiling of
$\lambda $
to be a bijective filling of the dominoes weakly above the main diagonal in a shifted tiling of
![]() $\lambda $
with entries in
$\lambda $
with entries in
![]() $[m]$
(where m is the number of dominoes weakly above the main diagonal) such that entries strictly increase from left to right along rows and from top to bottom in columns. See the right of Figure 2. Let
$[m]$
(where m is the number of dominoes weakly above the main diagonal) such that entries strictly increase from left to right along rows and from top to bottom in columns. See the right of Figure 2. Let
![]() $\mathsf {SShDT}(\lambda )$
denote the set of standard shifted domino tableaux of shape
$\mathsf {SShDT}(\lambda )$
denote the set of standard shifted domino tableaux of shape
![]() $\lambda $
. For
$\lambda $
. For
![]() $Q\in \mathsf {SShDT}(\lambda )$
, let
$Q\in \mathsf {SShDT}(\lambda )$
, let
![]() $\mathrm {dom}_i(Q)$
be the domino filled with the entry i in Q. A number
$\mathrm {dom}_i(Q)$
be the domino filled with the entry i in Q. A number
![]() $i\in [0,m-1]$
is a
$i\in [0,m-1]$
is a ![]() of Q if
of Q if
![]() $i=0$
and
$i=0$
and
![]() $\mathrm {dom}_1(Q)$
is vertical or if
$\mathrm {dom}_1(Q)$
is vertical or if
![]() $i>0$
and
$i>0$
and
![]() $\mathrm {dom}_{i+1}(Q)$
is strictly lower than
$\mathrm {dom}_{i+1}(Q)$
is strictly lower than
![]() $\mathrm {dom}_i(Q)$
. Let
$\mathrm {dom}_i(Q)$
. Let
![]() $\mathrm {Des}(Q)$
be the set of descents of Q. In Corollary 4.8, we will prove that
$\mathrm {Des}(Q)$
be the set of descents of Q. In Corollary 4.8, we will prove that
where
![]() $\Delta ^B$
is as defined in (2.1).
$\Delta ^B$
is as defined in (2.1).

Figure 2: A semistandard shifted domino tableau
![]() $T\in \mathsf {SSShDT}(\lambda )$
(left) and a standard shifted domino tableau
$T\in \mathsf {SSShDT}(\lambda )$
(left) and a standard shifted domino tableau
![]() $U\in \mathsf {SShDT}(\lambda )$
(right), where
$U\in \mathsf {SShDT}(\lambda )$
(right), where
![]() $\lambda =(7,7,6,5,1)$
. We have
$\lambda =(7,7,6,5,1)$
. We have
![]() $\mathrm {wt}(T)=(1,4,0,1,2,2)$
and
$\mathrm {wt}(T)=(1,4,0,1,2,2)$
and
![]() $\mathrm {Des}(U)=\{1,5,7,8\}$
.
$\mathrm {Des}(U)=\{1,5,7,8\}$
.
Define a ![]() to be a standard shifted domino tableau in which each entry is either primed or unprimed. (So a standard shifted domino tableau with n dominoes yields
to be a standard shifted domino tableau in which each entry is either primed or unprimed. (So a standard shifted domino tableau with n dominoes yields
![]() $2^n$
marked standard shifted domino tableaux.) Let
$2^n$
marked standard shifted domino tableaux.) Let
![]() $\mathsf {MSShDT}(\lambda )$
denote the set of marked standard shifted domino tableaux of shape
$\mathsf {MSShDT}(\lambda )$
denote the set of marked standard shifted domino tableaux of shape
![]() $\lambda $
. Given
$\lambda $
. Given
![]() $S\in \mathsf {MSShDT}(\lambda )$
, let
$S\in \mathsf {MSShDT}(\lambda )$
, let
![]() $\mathrm {demark}(S)\in \mathsf {SShDT}$
be the standard shifted domino tableau obtained by removing all primes from S. We write
$\mathrm {demark}(S)\in \mathsf {SShDT}$
be the standard shifted domino tableau obtained by removing all primes from S. We write
![]() $\mathrm {dom}_i(S)$
for the domino in S that contains i or
$\mathrm {dom}_i(S)$
for the domino in S that contains i or
![]() $i'$
(so
$i'$
(so
![]() $\mathrm {dom}_i(S)=\mathrm {dom}_i(\mathrm {demark}(S))$
). We say an index
$\mathrm {dom}_i(S)=\mathrm {dom}_i(\mathrm {demark}(S))$
). We say an index
![]() $i\in [0,n-1]$
is a
$i\in [0,n-1]$
is a ![]() of
of
![]() $S\in \mathsf {MSShDT}(\lambda )$
if one of the following holds:
$S\in \mathsf {MSShDT}(\lambda )$
if one of the following holds:
-
•
 $i=0$
, and either
$i=0$
, and either
 $1'$
is in S or
$1'$
is in S or
 $\mathrm {dom}_1(S)$
is vertical (or both);
$\mathrm {dom}_1(S)$
is vertical (or both); -
•
 $i>0$
, i is in S, and
$i>0$
, i is in S, and
 $i\in \mathrm {Des}(\mathrm {demark}(S))$
;
$i\in \mathrm {Des}(\mathrm {demark}(S))$
; -
•
 $i>0$
,
$i>0$
,
 $(i+1)'$
is in S, and
$(i+1)'$
is in S, and
 $i\not \in \mathrm {Des}(\mathrm {demark}(S))$
.
$i\not \in \mathrm {Des}(\mathrm {demark}(S))$
.
Let
![]() $\mathrm {Des}(S)$
denote the set of descents of S.
$\mathrm {Des}(S)$
denote the set of descents of S.
Lemma 4.5 Let
![]() $S\in \mathsf {MSShDT}(\lambda )$
. Suppose there exist
$S\in \mathsf {MSShDT}(\lambda )$
. Suppose there exist
![]() $i,j\in [n]$
with
$i,j\in [n]$
with
![]() $i<j$
such that one of the following holds:
$i<j$
such that one of the following holds:
-
(I) i and
 $j'$
are in S;
$j'$
are in S; -
(II) i and j are in S, and
 $\mathrm {dom}_j(S)$
is strictly lower than
$\mathrm {dom}_j(S)$
is strictly lower than
 $\mathrm {dom}_i(S)$
;
$\mathrm {dom}_i(S)$
; -
(III)
 $i'$
and
$i'$
and
 $j'$
are in S, and
$j'$
are in S, and
 $\mathrm {dom}_i(S)$
is weakly below
$\mathrm {dom}_i(S)$
is weakly below
 $\mathrm {dom}_j(S)$
.
$\mathrm {dom}_j(S)$
.
Then there is a descent of S in
![]() $[i,j-1]$
.
$[i,j-1]$
.
Proof Suppose by way of contradiction that there exist
![]() $i<j$
satisfying one of the conditions (I), (II), (III) such that there are no descents of S in
$i<j$
satisfying one of the conditions (I), (II), (III) such that there are no descents of S in
![]() $[i,j-1]$
. We may choose such i and j so as to minimize the quantity
$[i,j-1]$
. We may choose such i and j so as to minimize the quantity
![]() $j-i$
.
$j-i$
.
Suppose i and j satisfy condition (I). Then, there must exist
![]() $k\in [i,j-1]$
such that k and
$k\in [i,j-1]$
such that k and
![]() $(k+1)'$
are in S. But then k must be in
$(k+1)'$
are in S. But then k must be in
![]() $\mathrm {Des}(S)$
, which is a contradiction.
$\mathrm {Des}(S)$
, which is a contradiction.
Now suppose i and j satisfy condition (II). For every
![]() $k\in [i+1,j-1]$
, we know that k is in S since, otherwise, i and k would satisfy condition (I), contradicting the minimality of
$k\in [i+1,j-1]$
, we know that k is in S since, otherwise, i and k would satisfy condition (I), contradicting the minimality of
![]() $j-i$
. Since k is not a descent of S, it is not a descent of
$j-i$
. Since k is not a descent of S, it is not a descent of
![]() $\mathrm {demark}(S)$
. Thus,
$\mathrm {demark}(S)$
. Thus,
![]() $\mathrm {dom}_{k+1}(\mathrm {demark}(S))$
is not strictly lower than
$\mathrm {dom}_{k+1}(\mathrm {demark}(S))$
is not strictly lower than
![]() $\mathrm {dom}_k(\mathrm {demark}(S))$
. From the definition of a standard shifted domino tableau, the only way that part of
$\mathrm {dom}_k(\mathrm {demark}(S))$
. From the definition of a standard shifted domino tableau, the only way that part of
![]() $\mathrm {dom}_{k+1}(\mathrm {demark}(S))$
can be strictly lower than part of
$\mathrm {dom}_{k+1}(\mathrm {demark}(S))$
can be strictly lower than part of
![]() $\mathrm {dom}_k(\mathrm {demark}(S))$
is if
$\mathrm {dom}_k(\mathrm {demark}(S))$
is if
![]() $\mathrm {dom}_k(\mathrm {demark}(S))$
is horizontal,
$\mathrm {dom}_k(\mathrm {demark}(S))$
is horizontal,
![]() $\mathrm {dom}_{k+1}(\mathrm {demark}(S))$
is vertical and immediately right of
$\mathrm {dom}_{k+1}(\mathrm {demark}(S))$
is vertical and immediately right of
![]() $\mathrm {dom}_{k}(\mathrm {demark}(S))$
, and the main diagonal intersects both of these dominoes. To satisfy condition (II), both parts of
$\mathrm {dom}_{k}(\mathrm {demark}(S))$
, and the main diagonal intersects both of these dominoes. To satisfy condition (II), both parts of
![]() $\mathrm {dom}_j(\mathrm {demark}(S))$
must be strictly below both parts of
$\mathrm {dom}_j(\mathrm {demark}(S))$
must be strictly below both parts of
![]() $\mathrm {dom}_i(\mathrm {demark}(S))$
. This means the configuration described has to occur for at least two different values of k between i and j. But in any two occurrences of this configuration, both parts of each domino in the later occurrence are strictly below both parts of each domino in the earlier occurrence. Therefore, between two occurrences of this configuration, there must be some
$\mathrm {dom}_i(\mathrm {demark}(S))$
. This means the configuration described has to occur for at least two different values of k between i and j. But in any two occurrences of this configuration, both parts of each domino in the later occurrence are strictly below both parts of each domino in the earlier occurrence. Therefore, between two occurrences of this configuration, there must be some
![]() $\ell $
for which both parts of
$\ell $
for which both parts of
![]() $\mathrm {dom}_{\ell +1}(\mathrm {demark}(S))$
are strictly below both parts of
$\mathrm {dom}_{\ell +1}(\mathrm {demark}(S))$
are strictly below both parts of
![]() $\mathrm {dom}_{\ell }(\mathrm {demark}(S))$
, which contradicts the assumption that there are no descents of S in
$\mathrm {dom}_{\ell }(\mathrm {demark}(S))$
, which contradicts the assumption that there are no descents of S in
![]() $[i, j-1]$
.
$[i, j-1]$
.
Finally, suppose i and j satisfy condition (III). For every
![]() $k\in [i,j-1]$
, we know that
$k\in [i,j-1]$
, we know that
![]() $(k+1)'$
is in S since, otherwise,
$(k+1)'$
is in S since, otherwise,
![]() $k+1$
and j would satisfy condition (I), contradicting the minimality of
$k+1$
and j would satisfy condition (I), contradicting the minimality of
![]() $j-i$
. Since k is not a descent of S and
$j-i$
. Since k is not a descent of S and
![]() $(k+1)'$
is in S, we must have
$(k+1)'$
is in S, we must have
![]() $k\in \mathrm {Des}(\mathrm {demark}(S))$
. Thus,
$k\in \mathrm {Des}(\mathrm {demark}(S))$
. Thus,
![]() $\mathrm {dom}_{k+1}(\mathrm {demark}(S))$
is strictly lower than
$\mathrm {dom}_{k+1}(\mathrm {demark}(S))$
is strictly lower than
![]() $\mathrm {dom}_k(\mathrm {demark}(S))$
. As this is true for all
$\mathrm {dom}_k(\mathrm {demark}(S))$
. As this is true for all
![]() $k\in [i,j-1]$
, it follows that
$k\in [i,j-1]$
, it follows that
![]() $\mathrm {dom}_j(\mathrm {demark}(S))$
is strictly lower
$\mathrm {dom}_j(\mathrm {demark}(S))$
is strictly lower
![]() $\mathrm {dom}_i(\mathrm {demark}(S))$
, which contradicts our assumption that i and j satisfy condition (III).
$\mathrm {dom}_i(\mathrm {demark}(S))$
, which contradicts our assumption that i and j satisfy condition (III).
Given
![]() $T\in \mathsf {SSShDT}(\lambda )$
, let
$T\in \mathsf {SSShDT}(\lambda )$
, let
![]() $\mathrm {std}(T)\in \mathsf {MSShDT}(\lambda )$
be the
$\mathrm {std}(T)\in \mathsf {MSShDT}(\lambda )$
be the ![]() of T obtained as follows. Let
of T obtained as follows. Let
![]() $n_1 < n_2 < \dots <n_r$
be the positive integers i such that
$n_1 < n_2 < \dots <n_r$
be the positive integers i such that
![]() $\mathrm {wt}_i(T)\neq~0$
. Replace the
$\mathrm {wt}_i(T)\neq~0$
. Replace the
![]() $0$
entries in T from left to right with integers
$0$
entries in T from left to right with integers
![]() $1, 2, \ldots , \mathrm {wt}_0(T)$
. Then replace the entries
$1, 2, \ldots , \mathrm {wt}_0(T)$
. Then replace the entries
![]() $n_1^{\prime }$
and
$n_1^{\prime }$
and
![]() $n_1$
in T with
$n_1$
in T with
![]() $\mathrm {wt}_0(T)+1, \ldots , \mathrm {wt}_0(T)+\mathrm {wt}_{n_1}(T)$
or their primed versions (replacing primed entries with primed integers and unprimed entries with unprimed integers) in the following order: first replace entries
$\mathrm {wt}_0(T)+1, \ldots , \mathrm {wt}_0(T)+\mathrm {wt}_{n_1}(T)$
or their primed versions (replacing primed entries with primed integers and unprimed entries with unprimed integers) in the following order: first replace entries
![]() $n_1^{\prime }$
from top to bottom; then replace entries
$n_1^{\prime }$
from top to bottom; then replace entries
![]() $n_1$
from left to right. This is well defined since all
$n_1$
from left to right. This is well defined since all
![]() $n_1^{\prime }$
and
$n_1^{\prime }$
and
![]() $n_1$
entries appear either strictly below or strictly right of each
$n_1$
entries appear either strictly below or strictly right of each
![]() $0$
entry in T, the entries
$0$
entry in T, the entries
![]() $n_1^{\prime }$
form a vertical strip (no two dominoes in the same row both have entry
$n_1^{\prime }$
form a vertical strip (no two dominoes in the same row both have entry
![]() $n_1^{\prime }$
), the entries
$n_1^{\prime }$
), the entries
![]() $n_1$
form a horizontal strip (no two dominoes in the same column both have entry
$n_1$
form a horizontal strip (no two dominoes in the same column both have entry
![]() $n_1$
), and every
$n_1$
), and every
![]() $n_1$
is either strictly below or strictly right of each
$n_1$
is either strictly below or strictly right of each
![]() $n_1^{\prime }$
. Then continue in the same manner with
$n_1^{\prime }$
. Then continue in the same manner with
![]() $n_2^{\prime }$
and
$n_2^{\prime }$
and
![]() $n_2$
, and so on.
$n_2$
, and so on.
We now show that the semistandard shifted domino tableaux with a prescribed stardardization
![]() $S\in \mathsf {MSShDT}(\lambda )$
generate the type-B fundamental quasisymmetric function corresponding to the descent set of S.
$S\in \mathsf {MSShDT}(\lambda )$
generate the type-B fundamental quasisymmetric function corresponding to the descent set of S.
Theorem 4.6 Let
![]() $S\in \mathsf {MSShDT}(\lambda )$
. Then
$S\in \mathsf {MSShDT}(\lambda )$
. Then
 $$\begin{align*}\sum_{\substack{T\in \mathsf{SSShDT}(\lambda) \\ \mathrm{std}(T)=S}}\!\!\!\!\!x^{\mathrm{wt}(T)} = F^B_{\mathrm{Des}(S)}.\end{align*}$$
$$\begin{align*}\sum_{\substack{T\in \mathsf{SSShDT}(\lambda) \\ \mathrm{std}(T)=S}}\!\!\!\!\!x^{\mathrm{wt}(T)} = F^B_{\mathrm{Des}(S)}.\end{align*}$$
Proof Suppose
![]() $\mathrm {std}(T)=S$
, and let
$\mathrm {std}(T)=S$
, and let
![]() $n_1 < n_2 < \dots < n_r$
be the positive integers i such that
$n_1 < n_2 < \dots < n_r$
be the positive integers i such that
![]() $\mathrm {wt}_i(T)\neq 0$
. The semistandard shifted domino tableau T is obtained from S by replacing the entries
$\mathrm {wt}_i(T)\neq 0$
. The semistandard shifted domino tableau T is obtained from S by replacing the entries
![]() $1,2,\ldots ,\mathrm {wt}_0(T)$
with
$1,2,\ldots ,\mathrm {wt}_0(T)$
with
![]() $0$
, replacing the entries
$0$
, replacing the entries
![]() $\mathrm {wt}_0(T)+1, \ldots , \mathrm {wt}_0(T)+ \mathrm {wt}_{n_1}(T)$
with
$\mathrm {wt}_0(T)+1, \ldots , \mathrm {wt}_0(T)+ \mathrm {wt}_{n_1}(T)$
with
![]() $n_1$
, and so on, and keeping the primes in the same dominoes as in S. Let
$n_1$
, and so on, and keeping the primes in the same dominoes as in S. Let
![]() $T_i$
denote the entry that fills the domino
$T_i$
denote the entry that fills the domino
![]() $\mathrm {dom}_i(S)$
in the tableau T, and let
$\mathrm {dom}_i(S)$
in the tableau T, and let
![]() $|T_i|$
be the unprimed version of
$|T_i|$
be the unprimed version of
![]() $T_i$
(so if
$T_i$
(so if
![]() $T_i\in \{k',k\}$
, then
$T_i\in \{k',k\}$
, then
![]() $|T_i|=k$
).
$|T_i|=k$
).
We first show that
![]() $\{\mathrm {wt}_0(T), \mathrm {wt}_0(T)+\mathrm {wt}_{n_1}(T), \ldots ,\mathrm {wt}_0(T)+\mathrm {wt}_{n_1}(T)+\dots +\mathrm {wt}_{n_r}(T)\}$
contains
$\{\mathrm {wt}_0(T), \mathrm {wt}_0(T)+\mathrm {wt}_{n_1}(T), \ldots ,\mathrm {wt}_0(T)+\mathrm {wt}_{n_1}(T)+\dots +\mathrm {wt}_{n_r}(T)\}$
contains
![]() $\mathrm {Des}(S)$
; this is equivalent to showing that the monomial
$\mathrm {Des}(S)$
; this is equivalent to showing that the monomial
![]() $x^{\mathrm {wt}(T)}$
appears in
$x^{\mathrm {wt}(T)}$
appears in
![]() $F_{\mathrm {Des}(S)}^B$
. If
$F_{\mathrm {Des}(S)}^B$
. If
![]() $0\in \mathrm {Des}(S)$
, then the northwest-most domino is vertical or primed, hence cannot have the entry
$0\in \mathrm {Des}(S)$
, then the northwest-most domino is vertical or primed, hence cannot have the entry
![]() $0$
in T, so
$0$
in T, so
![]() $\mathrm {wt}_0(T)=0$
. Now consider a descent
$\mathrm {wt}_0(T)=0$
. Now consider a descent
![]() $i>0$
of S. We need to show that
$i>0$
of S. We need to show that
![]() $|T_i|<|T_{i+1}|$
. Suppose for a contradiction that
$|T_i|<|T_{i+1}|$
. Suppose for a contradiction that
![]() $|T_i|=|T_{i+1}|$
. If
$|T_i|=|T_{i+1}|$
. If
![]() $\mathrm {dom}_i(S)$
is strictly above
$\mathrm {dom}_i(S)$
is strictly above
![]() $\mathrm {dom}_{i+1}(S)$
, then i must be in S, and
$\mathrm {dom}_{i+1}(S)$
, then i must be in S, and
![]() $\mathrm {dom}_{i+1}(S)$
must be weakly left of
$\mathrm {dom}_{i+1}(S)$
must be weakly left of
![]() $\mathrm {dom}_i(S)$
. Then by definition of the standardization, the entry
$\mathrm {dom}_i(S)$
. Then by definition of the standardization, the entry
![]() $T_{i+1}$
(regardless of whether it is primed or unprimed) is standardized before
$T_{i+1}$
(regardless of whether it is primed or unprimed) is standardized before
![]() $T_i$
, contradicting the fact that
$T_i$
, contradicting the fact that
![]() $\mathrm {std}(T)=S$
. If
$\mathrm {std}(T)=S$
. If
![]() $(i+1)'$
is in S, then
$(i+1)'$
is in S, then
![]() $\mathrm {dom}_{i+1}(S)$
is weakly above and strictly right of
$\mathrm {dom}_{i+1}(S)$
is weakly above and strictly right of
![]() $\mathrm {dom}_i(S)$
, and it follows that the entry
$\mathrm {dom}_i(S)$
, and it follows that the entry
![]() $T_{i+1}$
is standardized before
$T_{i+1}$
is standardized before
![]() $T_i$
(regardless of whether
$T_i$
(regardless of whether
![]() $T_i$
is primed or unprimed), again contradicting the fact that
$T_i$
is primed or unprimed), again contradicting the fact that
![]() $\mathrm {std}(T)=S$
. Hence, if
$\mathrm {std}(T)=S$
. Hence, if
![]() $\mathrm {std}(T)=S$
, then
$\mathrm {std}(T)=S$
, then
![]() $x^{\mathrm {wt}(T)}$
is a term in
$x^{\mathrm {wt}(T)}$
is a term in
![]() $F^B_{\mathrm {Des}(S)}$
.
$F^B_{\mathrm {Des}(S)}$
.
Now, fix a term
![]() $x^b = x_0^{b_0}x_{n_1}^{b_{n_1}}x_{n_2}^{b_{n_2}}\dots $
in
$x^b = x_0^{b_0}x_{n_1}^{b_{n_1}}x_{n_2}^{b_{n_2}}\dots $
in
![]() $F^B_{\mathrm {Des}(S)}$
. Let T be obtained by replacing entries
$F^B_{\mathrm {Des}(S)}$
. Let T be obtained by replacing entries
![]() $1,2,\ldots , b_0$
in S with
$1,2,\ldots , b_0$
in S with
![]() $0$
, then replacing entries
$0$
, then replacing entries
![]() $b_0+1, \ldots , b_0+ b_{n_1}$
with
$b_0+1, \ldots , b_0+ b_{n_1}$
with
![]() $n_1$
, and so on, keeping the primes in the same dominoes as in S. By definition,
$n_1$
, and so on, keeping the primes in the same dominoes as in S. By definition,
![]() $\mathrm {wt}(T)=x^b$
. We need to show that T is the unique element of
$\mathrm {wt}(T)=x^b$
. We need to show that T is the unique element of
![]() $\mathsf {SSShDT}(\lambda )$
whose standardization is S. Note that since
$\mathsf {SSShDT}(\lambda )$
whose standardization is S. Note that since
![]() $x^b$
is a term in
$x^b$
is a term in
![]() $F^B_{\mathrm {Des}(S)}$
, the descent set of the type-B composition
$F^B_{\mathrm {Des}(S)}$
, the descent set of the type-B composition
![]() $(b_0,b_{n_1},b_{n_2}, \ldots )$
contains
$(b_0,b_{n_1},b_{n_2}, \ldots )$
contains
![]() $\mathrm {Des}(S)$
. In particular, if
$\mathrm {Des}(S)$
. In particular, if
![]() $i>0$
is a descent of S, then
$i>0$
is a descent of S, then
![]() ${|T_i|<|T_{i+1}|}$
, and if
${|T_i|<|T_{i+1}|}$
, and if
![]() $\mathrm {Des}(S)$
contains
$\mathrm {Des}(S)$
contains
![]() $0$
, then
$0$
, then
![]() $b_0=0$
.
$b_0=0$
.
We first show that
![]() $T\in \mathsf {SSShDT}(\lambda )$
. By definition, for each
$T\in \mathsf {SSShDT}(\lambda )$
. By definition, for each
![]() $i\ge 0$
, every domino containing
$i\ge 0$
, every domino containing
![]() $n_i$
or
$n_i$
or
![]() $n_i^{\prime }$
in T appears either strictly right of or strictly below every domino containing
$n_i^{\prime }$
in T appears either strictly right of or strictly below every domino containing
![]() $n_{i+1}$
or
$n_{i+1}$
or
![]() $n_{i+1}^{\prime }$
, so entries weakly increase along rows and columns. We need to check the conditions on
$n_{i+1}^{\prime }$
, so entries weakly increase along rows and columns. We need to check the conditions on
![]() $0$
entries and on primed and unprimed entries with the same value in rows and columns. If
$0$
entries and on primed and unprimed entries with the same value in rows and columns. If
![]() $b_0=0$
, there are no
$b_0=0$
, there are no
![]() $0$
entries in T to check. If
$0$
entries in T to check. If
![]() $b_0>0$
, then
$b_0>0$
, then
![]() $0\notin \mathrm {Des}(S)$
, so the northwest-most domino is horizontal. If a
$0\notin \mathrm {Des}(S)$
, so the northwest-most domino is horizontal. If a
![]() $0$
was placed in a primed domino in T, then the first instance of a
$0$
was placed in a primed domino in T, then the first instance of a
![]() $0$
being placed in a primed domino follows a
$0$
being placed in a primed domino follows a
![]() $0$
being placed in an unprimed domino to the left (or above), so these dominoes correspond to a descent in S, contradicting the fact that they both receive the value
$0$
being placed in an unprimed domino to the left (or above), so these dominoes correspond to a descent in S, contradicting the fact that they both receive the value
![]() $0$
. If a
$0$
. If a
![]() $0$
was placed in a domino strictly below a domino with entry
$0$
was placed in a domino strictly below a domino with entry
![]() $0$
, then there must have been an instance of a
$0$
, then there must have been an instance of a
![]() $0$
being placed in a domino strictly below the domino in which the previous
$0$
being placed in a domino strictly below the domino in which the previous
![]() $0$
was placed, and since both of these dominoes are unprimed, these dominoes correspond to a descent in S, contradicting the fact that they both received
$0$
was placed, and since both of these dominoes are unprimed, these dominoes correspond to a descent in S, contradicting the fact that they both received
![]() $0$
entries.
$0$
entries.
Now suppose that the dominoes containing
![]() $T_k$
and
$T_k$
and
![]() $T_{k+\ell }$
in T violate the conditions defining semistandard shifted domino tableaux, where
$T_{k+\ell }$
in T violate the conditions defining semistandard shifted domino tableaux, where
![]() $|T_k|=|T_{k+\ell }| = n_i$
. (Note that the domino containing
$|T_k|=|T_{k+\ell }| = n_i$
. (Note that the domino containing
![]() $T_{k+\ell }$
is strictly right of or strictly below the domino containing
$T_{k+\ell }$
is strictly right of or strictly below the domino containing
![]() $T_k$
.) Such a violation means that one of the following must hold:
$T_k$
.) Such a violation means that one of the following must hold:
-
•
 $T_k=n_i$
and
$T_k=n_i$
and
 $T_{k+\ell }=n_i^{\prime }$
, and these dominoes are in the same row or column;
$T_{k+\ell }=n_i^{\prime }$
, and these dominoes are in the same row or column; -
•
 $T_k=n_i$
and
$T_k=n_i$
and
 $T_{k+\ell }=n_i$
, and these dominoes are in the same column;
$T_{k+\ell }=n_i$
, and these dominoes are in the same column; -
•
 $T_k=n_i^{\prime }$
and
$T_k=n_i^{\prime }$
and
 $T_{k+\ell }=n_i^{\prime }$
, and these dominoes are in the same row.
$T_{k+\ell }=n_i^{\prime }$
, and these dominoes are in the same row.
By Lemma 4.5, there is a descent of S in the interval
![]() $[k, k+\ell -1]$
, which contradicts the fact that
$[k, k+\ell -1]$
, which contradicts the fact that
![]() $|T_j|=n_i$
for all
$|T_j|=n_i$
for all
![]() $k<j<k+\ell $
.
$k<j<k+\ell $
.
Next, observe that only T could possibly standardize to S. This is because the standardization procedure replaces all entries i in
![]() $K\in \mathsf {SSShDT}(\lambda )$
with integers that are smaller than those with which it replaces entries
$K\in \mathsf {SSShDT}(\lambda )$
with integers that are smaller than those with which it replaces entries
![]() $i+1$
. So if K standardizes to S, all
$i+1$
. So if K standardizes to S, all
![]() $0$
entries in K must be in the same dominoes as
$0$
entries in K must be in the same dominoes as
![]() $1, \ldots , b_0$
in S, all
$1, \ldots , b_0$
in S, all
![]() $n_1$
entries in K must be in the same dominoes as
$n_1$
entries in K must be in the same dominoes as
![]() $b_0+1, \ldots , b_0+b_{n_1}$
in S, etc, and the position of the primes is determined by S. So
$b_0+1, \ldots , b_0+b_{n_1}$
in S, etc, and the position of the primes is determined by S. So
![]() $K=T$
.
$K=T$
.
Finally, we must show that indeed
![]() $\mathrm {std}(T)=S$
. We must ensure that if
$\mathrm {std}(T)=S$
. We must ensure that if
![]() ${|T_k|=|T_{k+1}|=j}$
, then the entry
${|T_k|=|T_{k+1}|=j}$
, then the entry
![]() $T_k$
is standardized before the entry
$T_k$
is standardized before the entry
![]() $T_{k+1}$
. Note that
$T_{k+1}$
. Note that
![]() $|T_k|=|T_{k+1}|$
implies
$|T_k|=|T_{k+1}|$
implies
![]() $k\notin \mathrm {Des}(S)$
. Note that k and
$k\notin \mathrm {Des}(S)$
. Note that k and
![]() $(k+1)'$
cannot both be in S since this would force k to be a descent of S. If
$(k+1)'$
cannot both be in S since this would force k to be a descent of S. If
![]() $k'$
and
$k'$
and
![]() $k+1$
are in S, then by definition the standardization procedure encounters
$k+1$
are in S, then by definition the standardization procedure encounters
![]() $T_k=j'$
before
$T_k=j'$
before
![]() $T_{k+1}=j$
. If k and
$T_{k+1}=j$
. If k and
![]() $k+1$
are both in S, then since
$k+1$
are both in S, then since
![]() $k\notin \mathrm {Des}(S)$
,
$k\notin \mathrm {Des}(S)$
,
![]() $\mathrm {dom}_{k+1}(S)$
is strictly right of
$\mathrm {dom}_{k+1}(S)$
is strictly right of
![]() $\mathrm {dom}_k(S)$
. Hence,
$\mathrm {dom}_k(S)$
. Hence,
![]() $T_k=j$
is standardized before
$T_k=j$
is standardized before
![]() $T_{k+1}=j$
. If
$T_{k+1}=j$
. If
![]() $k'$
and
$k'$
and
![]() $(k+1)'$
are both in S, then since
$(k+1)'$
are both in S, then since
![]() $k\notin \mathrm {Des}(S)$
,
$k\notin \mathrm {Des}(S)$
,
![]() $\mathrm {dom}_{k+1}(S)$
is strictly below
$\mathrm {dom}_{k+1}(S)$
is strictly below
![]() $\mathrm {dom}_k(S)$
. Hence,
$\mathrm {dom}_k(S)$
. Hence,
![]() $T_k=j'$
is standardized before
$T_k=j'$
is standardized before
![]() $T_{k+1}=j'$
.
$T_{k+1}=j'$
.
Theorem 4.7 Let
![]() $\lambda $
be a pavable partition, and fix
$\lambda $
be a pavable partition, and fix
![]() $Q\in \mathsf {SShDT}(\lambda )$
. Then
$Q\in \mathsf {SShDT}(\lambda )$
. Then
 $$\begin{align*}\sum_{\substack{S\in \mathsf{MSShDT}(\lambda) \\ \mathrm{demark}(S)=Q} } F^B_{\mathrm{Des}(S)} = \Delta^B(\mathrm{Des}(Q)).\end{align*}$$
$$\begin{align*}\sum_{\substack{S\in \mathsf{MSShDT}(\lambda) \\ \mathrm{demark}(S)=Q} } F^B_{\mathrm{Des}(S)} = \Delta^B(\mathrm{Des}(Q)).\end{align*}$$
Proof Recall the notation from Section 2.1. Let us write
![]() $\mathrm {Peak}^B(Q)$
and
$\mathrm {Peak}^B(Q)$
and
![]() $\mathrm {Val}^B(Q)$
for the type-B peak set
$\mathrm {Val}^B(Q)$
for the type-B peak set
![]() $\mathrm {Peak}^B(\mathrm {Des}(Q))$
and the type-B valley set
$\mathrm {Peak}^B(\mathrm {Des}(Q))$
and the type-B valley set
![]() $\mathrm {Val}^B(\mathrm {Des}(Q))$
, respectively. Our goal is to show that
$\mathrm {Val}^B(\mathrm {Des}(Q))$
, respectively. Our goal is to show that
 $$\begin{align*}\sum_{\substack{S\in \mathsf{MSShDT}(\lambda) \\ \mathrm{demark}(S)=Q}} F^B_{\mathrm{Des}(S)} = \sum_{\substack{D\subseteq [0,n-1] \\ \mathrm{Peak}^B(Q)\subseteq D\triangle (D+1)}}2^{|\mathrm{Val}^B(Q)|}F^B_D.\end{align*}$$
$$\begin{align*}\sum_{\substack{S\in \mathsf{MSShDT}(\lambda) \\ \mathrm{demark}(S)=Q}} F^B_{\mathrm{Des}(S)} = \sum_{\substack{D\subseteq [0,n-1] \\ \mathrm{Peak}^B(Q)\subseteq D\triangle (D+1)}}2^{|\mathrm{Val}^B(Q)|}F^B_D.\end{align*}$$
Note that both sides of this equation have
![]() $2^n$
terms. We will first show that any
$2^n$
terms. We will first show that any
![]() ${S\in \mathsf {MSShDT}(\lambda )}$
such that
${S\in \mathsf {MSShDT}(\lambda )}$
such that
![]() $\mathrm {demark}(S)=Q$
satisfies
$\mathrm {demark}(S)=Q$
satisfies
![]() $\mathrm {Peak}^B(Q)\subseteq \mathrm {Des}(S)\triangle (\mathrm {Des}(S)+1)$
. We will then show that for every
$\mathrm {Peak}^B(Q)\subseteq \mathrm {Des}(S)\triangle (\mathrm {Des}(S)+1)$
. We will then show that for every
![]() $D\subseteq [0, n-1]$
, the set
$D\subseteq [0, n-1]$
, the set
![]() $\Gamma _D=\{S\in \mathsf {MSShDT}(\lambda ):\mathrm {demark}(S)=Q, \mathrm {Des}(S)=D\}$
has size
$\Gamma _D=\{S\in \mathsf {MSShDT}(\lambda ):\mathrm {demark}(S)=Q, \mathrm {Des}(S)=D\}$
has size
![]() $2^{|\mathrm {Val}^B(Q)|}$
.
$2^{|\mathrm {Val}^B(Q)|}$
.
Suppose
![]() $S\in \mathsf {MSShDT}(\lambda )$
and
$S\in \mathsf {MSShDT}(\lambda )$
and
![]() $\mathrm {demark}(S)=Q$
. Consider
$\mathrm {demark}(S)=Q$
. Consider
![]() $i\in [n-1]$
. Recall that
$i\in [n-1]$
. Recall that
![]() ${i\in \mathrm {Peak}^B(Q)}$
if and only if
${i\in \mathrm {Peak}^B(Q)}$
if and only if
![]() $i\in \mathrm {Des}(Q)$
and
$i\in \mathrm {Des}(Q)$
and
![]() $i-1\notin \mathrm {Des}(Q)$
. If
$i-1\notin \mathrm {Des}(Q)$
. If
![]() $i-1\notin \mathrm {Des}(Q)$
, then
$i-1\notin \mathrm {Des}(Q)$
, then
![]() $i-1\in \mathrm {Des}(S)$
if and only if
$i-1\in \mathrm {Des}(S)$
if and only if
![]() $i'$
is in S. Also, if
$i'$
is in S. Also, if
![]() $i\in \mathrm {Des}(Q)$
, then
$i\in \mathrm {Des}(Q)$
, then
![]() $i\in \mathrm {Des}(S)$
if and only if i is in S. Suppose
$i\in \mathrm {Des}(S)$
if and only if i is in S. Suppose
![]() $i\in \mathrm {Peak}^B(Q)$
. If
$i\in \mathrm {Peak}^B(Q)$
. If
![]() $i'$
is in S, then
$i'$
is in S, then
![]() $i-1\in \mathrm {Des}(S)$
and
$i-1\in \mathrm {Des}(S)$
and
![]() $i\notin \mathrm {Des}(S)$
, so
$i\notin \mathrm {Des}(S)$
, so
![]() $i\in \mathrm {Des}(S)\triangle (\mathrm {Des}(S)+1)$
. If i is in S, then
$i\in \mathrm {Des}(S)\triangle (\mathrm {Des}(S)+1)$
. If i is in S, then
![]() $i-1\notin \mathrm {Des}(S)$
and
$i-1\notin \mathrm {Des}(S)$
and
![]() $i\in \mathrm {Des}(S)$
, so again
$i\in \mathrm {Des}(S)$
, so again
![]() $i\in \mathrm {Des}(S)\triangle (\mathrm {Des}(S)+1)$
. This shows that
$i\in \mathrm {Des}(S)\triangle (\mathrm {Des}(S)+1)$
. This shows that
![]() $\mathrm {Peak}^B(Q)\subseteq \mathrm {Des}(S)\triangle (\mathrm {Des}(S)+1)$
.
$\mathrm {Peak}^B(Q)\subseteq \mathrm {Des}(S)\triangle (\mathrm {Des}(S)+1)$
.
Now suppose
![]() $D\subseteq [0,n-1]$
is such that
$D\subseteq [0,n-1]$
is such that
![]() $\mathrm {Peak}^B(Q)\subseteq D\triangle (D+1)$
, and define
$\mathrm {Peak}^B(Q)\subseteq D\triangle (D+1)$
, and define
![]() $\Gamma _D$
as above. First, we show
$\Gamma _D$
as above. First, we show
![]() $\Gamma _D$
is nonempty. Suppose
$\Gamma _D$
is nonempty. Suppose
![]() $\mathrm {Peak}^B(Q) = \{i_1, \ldots , i_r\}$
. The condition
$\mathrm {Peak}^B(Q) = \{i_1, \ldots , i_r\}$
. The condition
![]() $\mathrm {Peak}^B(Q)\subseteq D\triangle (D+1)$
implies that for each
$\mathrm {Peak}^B(Q)\subseteq D\triangle (D+1)$
implies that for each
![]() $1\le j \le r$
, precisely one of
$1\le j \le r$
, precisely one of
![]() $i_j -1$
or
$i_j -1$
or
![]() $i_j$
is in D. We construct
$i_j$
is in D. We construct
![]() $S\in \mathsf {MSShDT}(\lambda )$
such that
$S\in \mathsf {MSShDT}(\lambda )$
such that
![]() $\mathrm {demark}(S)=Q$
and
$\mathrm {demark}(S)=Q$
and
![]() $\mathrm {Des}(S)=D$
by considering the entries in Q from smallest to largest and choosing either to prime them or leave them unprimed. First, we consider the entries of Q in
$\mathrm {Des}(S)=D$
by considering the entries in Q from smallest to largest and choosing either to prime them or leave them unprimed. First, we consider the entries of Q in
![]() $[1, i_1]$
. We have two cases depending on whether
$[1, i_1]$
. We have two cases depending on whether
![]() $i_1=1$
or
$i_1=1$
or
![]() $i_1>1$
.
$i_1>1$
.
If
![]() $i_1=1$
, then we have
$i_1=1$
, then we have
![]() $1\in \mathrm {Des}(Q)$
and
$1\in \mathrm {Des}(Q)$
and
![]() $0\notin \mathrm {Des}(Q)$
. If
$0\notin \mathrm {Des}(Q)$
. If
![]() $0\in D$
, then we prime
$0\in D$
, then we prime
![]() $1$
, so
$1$
, so
![]() $0\in \mathrm {Des}(S)$
. Note that since
$0\in \mathrm {Des}(S)$
. Note that since
![]() $i_1=1$
and
$i_1=1$
and
![]() $0\in D$
, we must have
$0\in D$
, we must have
![]() $1\notin D$
; moreover,
$1\notin D$
; moreover,
![]() $1\notin \mathrm {Des}(S)$
since
$1\notin \mathrm {Des}(S)$
since
![]() $1\in \mathrm {Des}(Q)$
and
$1\in \mathrm {Des}(Q)$
and
![]() $1$
is primed. If
$1$
is primed. If
![]() $0\notin D$
, then we do not prime
$0\notin D$
, then we do not prime
![]() $1$
. Since
$1$
. Since
![]() $0\notin D$
and
$0\notin D$
and
![]() $i_1=1$
, we must have
$i_1=1$
, we must have
![]() $1\in D$
, and we will also have
$1\in D$
, and we will also have
![]() $1\in \mathrm {Des}(S)$
since
$1\in \mathrm {Des}(S)$
since
![]() $1\in \mathrm {Des}(Q)$
and
$1\in \mathrm {Des}(Q)$
and
![]() $1$
is unprimed.
$1$
is unprimed.
Now assume
![]() $i_1>1$
. By definition of the peak set of Q, any descents of Q that are smaller than
$i_1>1$
. By definition of the peak set of Q, any descents of Q that are smaller than
![]() $i_1$
form an initial segment in
$i_1$
form an initial segment in
![]() $[0, i_1-2]$
. Furthermore, since
$[0, i_1-2]$
. Furthermore, since
![]() $0\in \mathrm {Des}(Q)$
implies
$0\in \mathrm {Des}(Q)$
implies
![]() $\mathrm {dom}_1(Q)$
is vertical, we have
$\mathrm {dom}_1(Q)$
is vertical, we have
![]() $1\notin \mathrm {Des}(Q)$
whenever
$1\notin \mathrm {Des}(Q)$
whenever
![]() $0\in \mathrm {Des}(Q)$
. Hence, no number smaller than
$0\in \mathrm {Des}(Q)$
. Hence, no number smaller than
![]() $i_1$
can be a descent of Q, except possibly
$i_1$
can be a descent of Q, except possibly
![]() $0$
. Now, prime
$0$
. Now, prime
![]() $1$
if both
$1$
if both
![]() $0\in D$
and
$0\in D$
and
![]() $\mathrm {dom}_1(Q)$
is horizontal, and leave
$\mathrm {dom}_1(Q)$
is horizontal, and leave
![]() $1$
unprimed otherwise. This ensures that
$1$
unprimed otherwise. This ensures that
![]() $0\in \mathrm {Des}(S)$
if and only if
$0\in \mathrm {Des}(S)$
if and only if
![]() $0\in D$
. Next, for all
$0\in D$
. Next, for all
![]() $k\in D\cap [1, i_1-1]$
, prime the entry
$k\in D\cap [1, i_1-1]$
, prime the entry
![]() $k+1$
in Q, and leave all other entries unprimed. Since there are no descents of Q in the interval
$k+1$
in Q, and leave all other entries unprimed. Since there are no descents of Q in the interval
![]() $[1, i_1-1]$
, this ensures that, for
$[1, i_1-1]$
, this ensures that, for
![]() $k\in [1, i_1-1]$
, we will have
$k\in [1, i_1-1]$
, we will have
![]() $k\in \mathrm {Des}(S)$
if and only if
$k\in \mathrm {Des}(S)$
if and only if
![]() $k\in D$
. Finally, consider
$k\in D$
. Finally, consider
![]() $i_1$
, which by definition is in
$i_1$
, which by definition is in
![]() $\mathrm {Des}(Q)$
. If
$\mathrm {Des}(Q)$
. If
![]() $i_1-1\in D$
, then we have already primed
$i_1-1\in D$
, then we have already primed
![]() $i_1$
, and therefore
$i_1$
, and therefore
![]() $i_1$
will not be a descent of S, but this is precisely what is required since
$i_1$
will not be a descent of S, but this is precisely what is required since
![]() $i_1-1\in D$
implies
$i_1-1\in D$
implies
![]() $i_1\notin D$
. On the other hand, if
$i_1\notin D$
. On the other hand, if
![]() $i_1-1\notin D$
, then we have already chosen
$i_1-1\notin D$
, then we have already chosen
![]() $i_1$
to be unprimed, and then since
$i_1$
to be unprimed, and then since
![]() $i_1\in \mathrm {Des}(Q)$
, we have
$i_1\in \mathrm {Des}(Q)$
, we have
![]() $i_1\in \mathrm {Des}(S)$
. But again this is precisely what is required since
$i_1\in \mathrm {Des}(S)$
. But again this is precisely what is required since
![]() $i_1-1\notin D$
implies
$i_1-1\notin D$
implies
![]() $i_1\in D$
.
$i_1\in D$
.
Now consider the entries of Q in the interval
![]() $[i_1+1, i_2]$
. The descents of Q in this interval form a (possibly empty) initial segment in this interval, say
$[i_1+1, i_2]$
. The descents of Q in this interval form a (possibly empty) initial segment in this interval, say
![]() $[i_1+1, s_1]$
, where
$[i_1+1, s_1]$
, where
![]() $s_1 \le i_2-2$
. Leave unprimed the elements of
$s_1 \le i_2-2$
. Leave unprimed the elements of
![]() $[i_1+1, \ldots s_1]$
that are in D, and prime the elements of
$[i_1+1, \ldots s_1]$
that are in D, and prime the elements of
![]() $[i_1+1, \ldots s_1]$
that are not in D. The descents of S in this interval will then be precisely the elements of D in this interval. The entries in
$[i_1+1, \ldots s_1]$
that are not in D. The descents of S in this interval will then be precisely the elements of D in this interval. The entries in
![]() $[s_1+1 \ldots i_2-1]$
are not descents of Q. For each k in this interval, prime
$[s_1+1 \ldots i_2-1]$
are not descents of Q. For each k in this interval, prime
![]() $k+1$
if
$k+1$
if
![]() $k\in D$
, and leave
$k\in D$
, and leave
![]() $k+1$
unprimed if
$k+1$
unprimed if
![]() $k\not \in D$
. Then the descents of S in this interval are precisely the elements of D in this interval. Continue in this manner with the elements in the interval
$k\not \in D$
. Then the descents of S in this interval are precisely the elements of D in this interval. Continue in this manner with the elements in the interval
![]() $[i_2+1, i_3]$
and all subsequent intervals: the resulting
$[i_2+1, i_3]$
and all subsequent intervals: the resulting
![]() $\mathsf {MSShDT}$
S satisfies
$\mathsf {MSShDT}$
S satisfies
![]() $\mathrm {demark}(S)=Q$
and
$\mathrm {demark}(S)=Q$
and
![]() ${\mathrm {Des}(S)=D}$
.
${\mathrm {Des}(S)=D}$
.
Let
![]() $S^*\in \Gamma _D$
. We claim that
$S^*\in \Gamma _D$
. We claim that
![]() $\Gamma _D$
is equal to the set of tableau that can be obtained from
$\Gamma _D$
is equal to the set of tableau that can be obtained from
![]() $S^*$
by priming or unpriming some of the entries in
$S^*$
by priming or unpriming some of the entries in
![]() $\mathrm {Val}^B(Q)$
. Suppose
$\mathrm {Val}^B(Q)$
. Suppose
![]() $m\in \mathrm {Val}^B(Q)$
. Then
$m\in \mathrm {Val}^B(Q)$
. Then
![]() $m\notin \mathrm {Des}(Q)$
, so whether m is a descent in
$m\notin \mathrm {Des}(Q)$
, so whether m is a descent in
![]() $S^*$
is entirely controlled by whether
$S^*$
is entirely controlled by whether
![]() $m+1$
is primed or not, regardless of whether m is primed. Similarly, since
$m+1$
is primed or not, regardless of whether m is primed. Similarly, since
![]() $m-1\in \mathrm {Des}(Q)$
, whether
$m-1\in \mathrm {Des}(Q)$
, whether
![]() $m-1$
is a descent in
$m-1$
is a descent in
![]() $S^*$
is entirely controlled by whether
$S^*$
is entirely controlled by whether
![]() $m-1$
is primed or not, regardless of whether m is primed. Thus, priming or unpriming m does not change the descent set. On the other hand, every integer
$m-1$
is primed or not, regardless of whether m is primed. Thus, priming or unpriming m does not change the descent set. On the other hand, every integer
![]() $p\in [n]\setminus \mathrm {Val}^B(Q)$
is such that either
$p\in [n]\setminus \mathrm {Val}^B(Q)$
is such that either
![]() $p\in \mathrm {Des}(Q)$
(in which case priming or unpriming p changes whether
$p\in \mathrm {Des}(Q)$
(in which case priming or unpriming p changes whether
![]() $p+1$
is in the descent set of the tableau), or
$p+1$
is in the descent set of the tableau), or
![]() $p-1\notin \mathrm {Des}(Q)$
(in which case priming or unpriming p changes whether
$p-1\notin \mathrm {Des}(Q)$
(in which case priming or unpriming p changes whether
![]() $p-1$
is in the descent set of the tableau).
$p-1$
is in the descent set of the tableau).
From Theorems 4.6 and 4.7 we conclude the following.
Corollary 4.8 Let
![]() $\lambda $
be a pavable partition. The shifted domino function
$\lambda $
be a pavable partition. The shifted domino function
![]() $H_\lambda $
satisfies
$H_\lambda $
satisfies
5 0-Hecke–Clifford algebras in type B
The ![]()
![]() $Cl_n$
is the
$Cl_n$
is the
![]() $\mathbb C$
-algebra with generators
$\mathbb C$
-algebra with generators
![]() $c_1,\ldots , c_n$
subject to the relations
$c_1,\ldots , c_n$
subject to the relations
![]() ${c_j^2 = -1}$
and
${c_j^2 = -1}$
and
![]() $c_ic_j=-c_jc_i$
for
$c_ic_j=-c_jc_i$
for
![]() $i\neq j$
. The
$i\neq j$
. The ![]()
![]() $HCl_n(0)$
is the
$HCl_n(0)$
is the
![]() $\mathbb C$
-algebra generated by the (type-A)
$\mathbb C$
-algebra generated by the (type-A)
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $H_n(0)$
and the Clifford algebra
$H_n(0)$
and the Clifford algebra
![]() $Cl_n$
such that the generators
$Cl_n$
such that the generators
![]() $\pi _1,\ldots ,\pi _{n-1},c_1,\ldots ,c_n$
satisfy the additional relations
$\pi _1,\ldots ,\pi _{n-1},c_1,\ldots ,c_n$
satisfy the additional relations
 $$ \begin{align*} \pi_ic_j & = c_j\pi_i \,\,\,\, \mbox{ for } j\neq i, i+1; \\ \pi_ic_i & = c_{i+1}\pi_i; \\ (\pi_i+1)c_{i+1} & = c_i(\pi_i+1). \end{align*} $$
$$ \begin{align*} \pi_ic_j & = c_j\pi_i \,\,\,\, \mbox{ for } j\neq i, i+1; \\ \pi_ic_i & = c_{i+1}\pi_i; \\ (\pi_i+1)c_{i+1} & = c_i(\pi_i+1). \end{align*} $$
We now introduce the ![]()
![]() $HCl_n^B(0)$
as the algebra generated by the
$HCl_n^B(0)$
as the algebra generated by the
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $H_n^B(0)$
and the Clifford algebra
$H_n^B(0)$
and the Clifford algebra
![]() $Cl_n$
such that the generators
$Cl_n$
such that the generators
![]() $\pi _0,\ldots ,\pi _{n-1},c_1,\ldots ,c_n$
satisfy the additional relations
$\pi _0,\ldots ,\pi _{n-1},c_1,\ldots ,c_n$
satisfy the additional relations
 $$ \begin{align*} \pi_ic_j & = c_j\pi_i \hspace{1.52cm} \mbox{ for } j\neq i, i+1; \\ \pi_ic_{i+1} & = c_{i}\pi_i \hspace{1.55cm} \mbox{ for } 1\le i \le n-1; \\ (\pi_i+1)c_i & = c_{i+1}(\pi_i+1) \hspace{.2cm} \mbox{ for } 1\le i \le n-1; \\ \pi_0c_1 & = \sqrt{-1}\pi_0. \end{align*} $$
$$ \begin{align*} \pi_ic_j & = c_j\pi_i \hspace{1.52cm} \mbox{ for } j\neq i, i+1; \\ \pi_ic_{i+1} & = c_{i}\pi_i \hspace{1.55cm} \mbox{ for } 1\le i \le n-1; \\ (\pi_i+1)c_i & = c_{i+1}(\pi_i+1) \hspace{.2cm} \mbox{ for } 1\le i \le n-1; \\ \pi_0c_1 & = \sqrt{-1}\pi_0. \end{align*} $$
Note the differences between these relations and the relations defining the
![]() $0$
-Hecke–Clifford algebra in type A. These differences end up being necessary in order to make the algebra and combinatorics work out correctly.
$0$
-Hecke–Clifford algebra in type A. These differences end up being necessary in order to make the algebra and combinatorics work out correctly.
We now study the structure of the
![]() $HCl_n^B(0)$
-modules induced from the simple
$HCl_n^B(0)$
-modules induced from the simple
![]() $H_n^B(0)$
-modules. We give a tableau description of the basis elements of these modules and show that the type-B quasisymmetric characteristics of the restrictions of these modules to
$H_n^B(0)$
-modules. We give a tableau description of the basis elements of these modules and show that the type-B quasisymmetric characteristics of the restrictions of these modules to
![]() $H_n^B(0)$
are the type-B peak functions, thus giving a representation–theoretic interpretation of such functions. Moreover, we show that the isomorphism classes of these induced modules are indexed by the type-B peak sets. We proceed in a manner similar to [Reference Bergeron, Hivert and Thibon3, Sections 5.2 and 5.3], where analogous results are obtained in type A.
$H_n^B(0)$
are the type-B peak functions, thus giving a representation–theoretic interpretation of such functions. Moreover, we show that the isomorphism classes of these induced modules are indexed by the type-B peak sets. We proceed in a manner similar to [Reference Bergeron, Hivert and Thibon3, Sections 5.2 and 5.3], where analogous results are obtained in type A.
For each subset
![]() $D=\{d_1<\dots <d_r\}\subseteq [n]$
, we write
$D=\{d_1<\dots <d_r\}\subseteq [n]$
, we write
![]() $c_D$
for the element
$c_D$
for the element
![]() $c_{d_1}\dots c_{d_r}$
(with indices in increasing order). For each
$c_{d_1}\dots c_{d_r}$
(with indices in increasing order). For each
![]() $I\subseteq [0,n-1]$
, let us fix a nonzero vector
$I\subseteq [0,n-1]$
, let us fix a nonzero vector
![]() $\varepsilon _I$
in the simple
$\varepsilon _I$
in the simple
![]() $H_n^B(0)$
-module
$H_n^B(0)$
-module
![]() $\mathcal S_I^B$
so that
$\mathcal S_I^B$
so that
![]() $\mathcal S_I^B=\mathbb C\{\varepsilon _I\}$
. Recall that the module structure is defined by
$\mathcal S_I^B=\mathbb C\{\varepsilon _I\}$
. Recall that the module structure is defined by
 $$\begin{align*}\pi_j\cdot\varepsilon_I = \begin{cases} -\varepsilon_I & \mbox{ if } j\in I \\ 0 & \mbox{ if } j\notin I. \end{cases}\end{align*}$$
$$\begin{align*}\pi_j\cdot\varepsilon_I = \begin{cases} -\varepsilon_I & \mbox{ if } j\in I \\ 0 & \mbox{ if } j\notin I. \end{cases}\end{align*}$$
Let
be the
![]() $HCl_n^B(0)$
-module induced by
$HCl_n^B(0)$
-module induced by
![]() $\mathcal S_I^B$
. The set
$\mathcal S_I^B$
. The set
![]() $\{c_D\varepsilon _I:D\subseteq [n]\}$
is a linear basis for
$\{c_D\varepsilon _I:D\subseteq [n]\}$
is a linear basis for
![]() $\mathcal M_I$
.
$\mathcal M_I$
.
It will be convenient to represent a subset
![]() $I\subseteq [0,n-1]$
by a ribbon shape with
$I\subseteq [0,n-1]$
by a ribbon shape with
![]() $n+1$
boxes filled with
$n+1$
boxes filled with
![]() $0,1,\ldots ,n$
such that box filled with
$0,1,\ldots ,n$
such that box filled with
![]() $i+1$
is immediately below the box filled with i if
$i+1$
is immediately below the box filled with i if
![]() $i\in I$
and is immediately left of the box filled with i if
$i\in I$
and is immediately left of the box filled with i if
![]() $i\not \in I$
. We can then represent the element
$i\not \in I$
. We can then represent the element
![]() $c_D\varepsilon _I$
of
$c_D\varepsilon _I$
of
![]() $\mathcal M_I$
by replacing each entry
$\mathcal M_I$
by replacing each entry
![]() $d\in D$
with
$d\in D$
with
![]() $\overline d$
. For example, if
$\overline d$
. For example, if
![]() $n=7$
, then
$n=7$
, then

represents
![]() $c_{\{1,2,5\}}\varepsilon _{\{0,3,4,6\}}$
.
$c_{\{1,2,5\}}\varepsilon _{\{0,3,4,6\}}$
.
To describe the module structure of
![]() $\mathcal M_I$
, we need to see how each generator
$\mathcal M_I$
, we need to see how each generator
![]() $\pi _i$
acts on each basis element
$\pi _i$
acts on each basis element
![]() $c_D\varepsilon _I$
. Representing this basis element via a filled ribbon as above, we find that
$c_D\varepsilon _I$
. Representing this basis element via a filled ribbon as above, we find that
![]() $\pi _i\cdot c_D\varepsilon _I$
only depends on the boxes filled with i and
$\pi _i\cdot c_D\varepsilon _I$
only depends on the boxes filled with i and
![]() $i+1$
; hence, we can describe the action by drawing these two boxes and ignoring all others. For
$i+1$
; hence, we can describe the action by drawing these two boxes and ignoring all others. For
![]() $1\leq i\leq n-1$
, we have
$1\leq i\leq n-1$
, we have

Moreover, we have
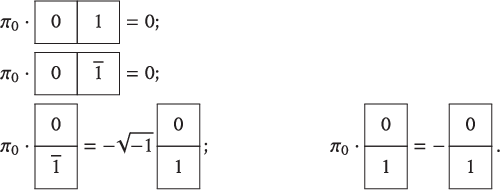
For a fixed
![]() $I\subseteq [0,n-1]$
, we define a partial order
$I\subseteq [0,n-1]$
, we define a partial order
![]() $\leq _I$
on the basis
$\leq _I$
on the basis
![]() $\{c_D\varepsilon _I:D\subseteq [n]\}$
via the covering relations of the form
$\{c_D\varepsilon _I:D\subseteq [n]\}$
via the covering relations of the form

for
![]() $1\leq i\leq n-1$
and the additional cover relation
$1\leq i\leq n-1$
and the additional cover relation

In this notation, each cover relation occurs when the ribbon diagrams agree except in the displayed boxes. For example, the first of these cover relations should be interpreted as saying
![]() $c_D\varepsilon _I\lessdot _I c_{D'}\varepsilon _I$
whenever
$c_D\varepsilon _I\lessdot _I c_{D'}\varepsilon _I$
whenever
![]() $i\notin I$
,
$i\notin I$
,
![]() $i\in D$
,
$i\in D$
,
![]() $i+1\not \in D$
, and
$i+1\not \in D$
, and
![]() $D'=(D\setminus \{i\})\cup \{i+1\}$
. The final additional cover relation says that
$D'=(D\setminus \{i\})\cup \{i+1\}$
. The final additional cover relation says that
![]() $c_D\varepsilon _I\lessdot _I c_{D'}\varepsilon _I$
whenever
$c_D\varepsilon _I\lessdot _I c_{D'}\varepsilon _I$
whenever
![]() $0\in I$
,
$0\in I$
,
![]() $1\in D$
, and
$1\in D$
, and
![]() $D'=D\setminus \{1\}$
.
$D'=D\setminus \{1\}$
.
The following lemma is immediate from the above discussion.
Lemma 5.1 Fix
![]() $I\subseteq [0,n-1]$
. For each
$I\subseteq [0,n-1]$
. For each
![]() $0\leq i\leq n-1$
, the action of
$0\leq i\leq n-1$
, the action of
![]() $\pi _i$
on the basis
$\pi _i$
on the basis
![]() $\{c_D\varepsilon _I:D\subseteq [n]\}$
of
$\{c_D\varepsilon _I:D\subseteq [n]\}$
of
![]() $\mathcal M_I$
is triangular with respect to the partial order
$\mathcal M_I$
is triangular with respect to the partial order
![]() $\leq _I$
. More precisely, for each
$\leq _I$
. More precisely, for each
![]() $D\subseteq [n]$
, we have
$D\subseteq [n]$
, we have
for some
![]() $\alpha (i,I,D)\in \{0,-1\}$
and some
$\alpha (i,I,D)\in \{0,-1\}$
and some
![]() $\beta (i,I,D')\in \mathbb C$
.
$\beta (i,I,D')\in \mathbb C$
.
Upon inspection, we find that the eigenvalue
![]() $\alpha (i,I,D)$
is equal to
$\alpha (i,I,D)$
is equal to
![]() $-1$
if and only if one of the following conditions holds:
$-1$
if and only if one of the following conditions holds:
-
•
 $i\notin I$
and
$i\notin I$
and
 $i\in D$
;
$i\in D$
; -
•
 $i\in I$
and
$i\in I$
and
 $i+1\notin D$
.
$i+1\notin D$
.
This implies that if v is in the type-B valley set
![]() $\mathrm {Val}^B([0,n-1]\setminus I)=([n]\cap I)\setminus (I+1)$
, then none of the eigenvalues
$\mathrm {Val}^B([0,n-1]\setminus I)=([n]\cap I)\setminus (I+1)$
, then none of the eigenvalues
![]() $\alpha (i,I,D)$
depend on whether or not v belongs to D. In other words, we have the following lemma.
$\alpha (i,I,D)$
depend on whether or not v belongs to D. In other words, we have the following lemma.
Lemma 5.2 If
![]() $v\in \mathrm {Val}^B([0,n-1]\setminus I)$
, then
$v\in \mathrm {Val}^B([0,n-1]\setminus I)$
, then
for every
![]() $i\in [0,n-1]$
and every
$i\in [0,n-1]$
and every
![]() $D\subseteq [n]$
.
$D\subseteq [n]$
.
Fix a linear extension
![]() $c_{D_1}\varepsilon _I,\ldots ,c_{D_{2^n}}\varepsilon _I$
of the partial order
$c_{D_1}\varepsilon _I,\ldots ,c_{D_{2^n}}\varepsilon _I$
of the partial order
![]() $\leq _I$
. For each
$\leq _I$
. For each
![]() $0\leq k\leq 2^n$
, it follows from Lemma 5.1 that the vector space
$0\leq k\leq 2^n$
, it follows from Lemma 5.1 that the vector space
![]() $\mathcal M_I^{(k)}=\mathbb C\{c_{D_1}\varepsilon _I,\ldots ,c_{D_k}\varepsilon _I\}$
is an
$\mathcal M_I^{(k)}=\mathbb C\{c_{D_1}\varepsilon _I,\ldots ,c_{D_k}\varepsilon _I\}$
is an
![]() $H_n^B(0)$
-module. Thus,
$H_n^B(0)$
-module. Thus,
is a composition series for the
![]() $H_n^B(0)$
-module obtained by restricting
$H_n^B(0)$
-module obtained by restricting
![]() $\mathcal M_I$
.
$\mathcal M_I$
.
For each
![]() $1\leq k\leq 2^n$
, the quotient
$1\leq k\leq 2^n$
, the quotient
![]() $\mathcal M_I^{(k)}/\mathcal M_I^{(k-1)}$
is a simple
$\mathcal M_I^{(k)}/\mathcal M_I^{(k-1)}$
is a simple
![]() $H_n^B(0)$
-module, so there is a unique subset
$H_n^B(0)$
-module, so there is a unique subset
![]() $K(k,I)\subseteq [0,n-1]$
such that
$K(k,I)\subseteq [0,n-1]$
such that
![]() $\mathcal M_I^{(k)}/\mathcal M_I^{(k-1)}$
is isomorphic to
$\mathcal M_I^{(k)}/\mathcal M_I^{(k-1)}$
is isomorphic to
![]() $\mathcal S_{K(k,I)}^B=\mathbb C\{\varepsilon _{K(k,I)}\}$
. According to Lemma 5.1, each generator
$\mathcal S_{K(k,I)}^B=\mathbb C\{\varepsilon _{K(k,I)}\}$
. According to Lemma 5.1, each generator
![]() $\pi _i$
acts on
$\pi _i$
acts on
![]() $\mathcal M_I^{(k)}/\mathcal M_I^{(k-1)}$
via multiplication by
$\mathcal M_I^{(k)}/\mathcal M_I^{(k-1)}$
via multiplication by
![]() $\alpha (i,I,D_k)$
. Therefore, it follows from the explicit description of the module structure of
$\alpha (i,I,D_k)$
. Therefore, it follows from the explicit description of the module structure of
![]() $\mathcal S_{K(k,I)}^B$
that
$\mathcal S_{K(k,I)}^B$
that
The next theorem allows us to interpret Petersen’s type-B peak functions as the type-B quasisymmetric characteristics of the restrictions of the modules
![]() $\mathcal M_I$
, thereby providing a type-B analogue of [Reference Bergeron, Hivert and Thibon3, Theorem 5.3]. We remark that while the paper [Reference Bergeron, Hivert and Thibon3] works directly with a set
$\mathcal M_I$
, thereby providing a type-B analogue of [Reference Bergeron, Hivert and Thibon3, Theorem 5.3]. We remark that while the paper [Reference Bergeron, Hivert and Thibon3] works directly with a set
![]() $I\in [n-1]$
, we must take the complement of our set I in
$I\in [n-1]$
, we must take the complement of our set I in
![]() ${[0,n-1]}$
in order to deal with the slight differences between the relations defining
${[0,n-1]}$
in order to deal with the slight differences between the relations defining
![]() $HCl_n^B(0)$
and those defining
$HCl_n^B(0)$
and those defining
![]() $HCl_n(0)$
.
$HCl_n(0)$
.
Theorem 5.3 For each
![]() $I\subseteq [0,n-1]$
, we have
$I\subseteq [0,n-1]$
, we have
Proof Consider
![]() $1\leq k\leq 2^n$
. Suppose
$1\leq k\leq 2^n$
. Suppose
![]() $p\in \mathrm {Peak}^B([0,n-1]\setminus I)$
; that is,
$p\in \mathrm {Peak}^B([0,n-1]\setminus I)$
; that is,
![]() $p-1\in I$
and
$p-1\in I$
and
![]() $p\notin I$
. If
$p\notin I$
. If
![]() ${p\in K(k,I)}$
, then it follows from (5.1) that
${p\in K(k,I)}$
, then it follows from (5.1) that
![]() $p\in D_k$
, so
$p\in D_k$
, so
![]() $p-1\not \in K(k,I)$
. On the other hand, if
$p-1\not \in K(k,I)$
. On the other hand, if
![]() ${p\notin K(k,I)}$
, then
${p\notin K(k,I)}$
, then
![]() $p\not \in D_k$
, so
$p\not \in D_k$
, so
![]() $p-1\in K(k,I)$
. This shows that
$p-1\in K(k,I)$
. This shows that
Also, note that if
![]() $0\notin I$
, then
$0\notin I$
, then
![]() $0\notin K(k,I)$
since
$0\notin K(k,I)$
since
![]() $D_k\subseteq [n]$
. Given a set
$D_k\subseteq [n]$
. Given a set
![]() $K\subseteq [0,n-1]$
such that
$K\subseteq [0,n-1]$
such that
![]() $\mathrm {Peak}^B([0,n-1]\setminus I)\subseteq K\triangle (K+1)$
and
$\mathrm {Peak}^B([0,n-1]\setminus I)\subseteq K\triangle (K+1)$
and
![]() $0\notin I\implies 0\notin K$
, it follows from Lemma 5.2 that the indices k satisfying
$0\notin I\implies 0\notin K$
, it follows from Lemma 5.2 that the indices k satisfying
![]() $K(k,I)=K$
are in bijection with subsets of
$K(k,I)=K$
are in bijection with subsets of
![]() ${\mathrm {Val}^B([0,n-1]\setminus I)}$
. Hence,
${\mathrm {Val}^B([0,n-1]\setminus I)}$
. Hence,
 $$ \begin{align*} \mathrm{ch}^B(\mathrm{Res}_{H_n^B(0)}(\mathcal M_I))&=\sum_{k=1}^{2^n}\mathrm{ch}^B(\mathcal M_I^{(k)}/\mathcal M_I^{(k-1)}) \\ &=\sum_{k=1}^{2^n}\mathrm{ch}^B(\mathcal S_{K(k,I)}^B) \\ &=\sum_{k=1}^{2^n}F^B_{K(k,I)} \\ &=2^{|\mathrm{Val}^B([0,n-1]\setminus I)|}\sum_{\substack{\mathrm{Peak}^B([0,n-1]\setminus I)\subseteq K\triangle(K+1) \\ 0\notin I\implies 0\notin K}}F_K^B \\ &=2^{|\mathrm{Peak}^B([0,n-1]\setminus I)|+\zeta([0,n-1]\setminus I)}\sum_{\substack{\mathrm{Peak}^B([0,n-1]\setminus I)\subseteq K'\triangle(K'+1) \\ 0\in [0,n-1]\setminus I\implies 0\in K'}}F_{K'}^B, \end{align*} $$
$$ \begin{align*} \mathrm{ch}^B(\mathrm{Res}_{H_n^B(0)}(\mathcal M_I))&=\sum_{k=1}^{2^n}\mathrm{ch}^B(\mathcal M_I^{(k)}/\mathcal M_I^{(k-1)}) \\ &=\sum_{k=1}^{2^n}\mathrm{ch}^B(\mathcal S_{K(k,I)}^B) \\ &=\sum_{k=1}^{2^n}F^B_{K(k,I)} \\ &=2^{|\mathrm{Val}^B([0,n-1]\setminus I)|}\sum_{\substack{\mathrm{Peak}^B([0,n-1]\setminus I)\subseteq K\triangle(K+1) \\ 0\notin I\implies 0\notin K}}F_K^B \\ &=2^{|\mathrm{Peak}^B([0,n-1]\setminus I)|+\zeta([0,n-1]\setminus I)}\sum_{\substack{\mathrm{Peak}^B([0,n-1]\setminus I)\subseteq K'\triangle(K'+1) \\ 0\in [0,n-1]\setminus I\implies 0\in K'}}F_{K'}^B, \end{align*} $$
where we obtained the last equality by using the identity (2.2) and substituting
![]() ${K'=[0,n-1]\setminus K}$
. The desired result now follows immediately from the definition of
${K'=[0,n-1]\setminus K}$
. The desired result now follows immediately from the definition of
![]() $\Delta ^B([0,n-1]\setminus I)$
.
$\Delta ^B([0,n-1]\setminus I)$
.
The proof of the following result is essentially the same as that of [Reference Bergeron, Hivert and Thibon3, Theorem 5.4], but we include it anyway for the sake of completeness.
Theorem 5.4 Suppose
![]() $I\subseteq [0,n-1]$
, and let
$I\subseteq [0,n-1]$
, and let
![]() $V=\mathrm {Val}^B([0,n-1]\setminus I)$
. Let
$V=\mathrm {Val}^B([0,n-1]\setminus I)$
. Let
![]() $Cl_V$
be the subalgebra of
$Cl_V$
be the subalgebra of
![]() $Cl_n$
generated by
$Cl_n$
generated by
![]() $\{c_v:v\in V\}$
. For
$\{c_v:v\in V\}$
. For
![]() $c\in Cl_n$
, define
$c\in Cl_n$
, define
![]() $f_c\colon \mathcal M_I\to \mathcal M_I$
by
$f_c\colon \mathcal M_I\to \mathcal M_I$
by
![]() $f_c(x\varepsilon _I)=xc\varepsilon _I$
for all
$f_c(x\varepsilon _I)=xc\varepsilon _I$
for all
![]() $x\in Cl_n$
. We obtain a right action of
$x\in Cl_n$
. We obtain a right action of
![]() $Cl_V$
on
$Cl_V$
on
![]() $\mathcal M_I$
by letting
$\mathcal M_I$
by letting
![]() $(x\varepsilon _I)\cdot c=f_c(x\varepsilon _I)$
(and extending by linearity), and this right action commutes with the left action of
$(x\varepsilon _I)\cdot c=f_c(x\varepsilon _I)$
(and extending by linearity), and this right action commutes with the left action of
![]() $HCl_n^B(0)$
. Moreover, the map
$HCl_n^B(0)$
. Moreover, the map
![]() $c\mapsto f_c$
is an isomorphism from
$c\mapsto f_c$
is an isomorphism from
![]() $Cl_V$
to
$Cl_V$
to
![]() $\mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
.
$\mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
.
Proof Because
![]() $\mathcal M_I$
is freely generated by
$\mathcal M_I$
is freely generated by
![]() $\varepsilon _I$
as a
$\varepsilon _I$
as a
![]() $Cl_n$
-module, each of the endomorphisms in
$Cl_n$
-module, each of the endomorphisms in
![]() $\mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
must be of the form
$\mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
must be of the form
![]() $f_c$
for a unique
$f_c$
for a unique
![]() $c\in Cl_n$
. Therefore, it suffices to prove that
$c\in Cl_n$
. Therefore, it suffices to prove that
![]() $f_c\in \mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
if and only if
$f_c\in \mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
if and only if
![]() $c\in Cl_V$
. Because every element of
$c\in Cl_V$
. Because every element of
![]() $HCl_n^B(0)$
can be written in the form
$HCl_n^B(0)$
can be written in the form
![]() $x\pi _{i_1}\dots \pi _{i_\ell }$
for some
$x\pi _{i_1}\dots \pi _{i_\ell }$
for some
![]() $x\in Cl_n$
and some
$x\in Cl_n$
and some
![]() $i_1,\ldots ,i_\ell \in [0,n-1]$
, we have
$i_1,\ldots ,i_\ell \in [0,n-1]$
, we have
![]() $f_c\in \mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
if and only if
$f_c\in \mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
if and only if
 $$ \begin{align} \pi_i\cdot c\,\varepsilon_I=\begin{cases} -c\,\varepsilon_I & \mbox{ if } i\in I \\ 0 & \mbox{ if } i\not\in I \end{cases} \end{align} $$
$$ \begin{align} \pi_i\cdot c\,\varepsilon_I=\begin{cases} -c\,\varepsilon_I & \mbox{ if } i\in I \\ 0 & \mbox{ if } i\not\in I \end{cases} \end{align} $$
for every
![]() $i\in [0,n-1]$
.
$i\in [0,n-1]$
.
First, suppose
![]() $c=c_D$
for some
$c=c_D$
for some
![]() $D\subseteq V$
. In the ribbon diagram of
$D\subseteq V$
. In the ribbon diagram of
![]() $c_D\varepsilon _I$
, no box with a barred entry has a box immediately above it or immediately to its right. For each
$c_D\varepsilon _I$
, no box with a barred entry has a box immediately above it or immediately to its right. For each
![]() $i\in [0,n-1]$
, it follows from the above explicit description of the action of
$i\in [0,n-1]$
, it follows from the above explicit description of the action of
![]() $\pi _i$
on
$\pi _i$
on
![]() $c_D\varepsilon _I$
that
$c_D\varepsilon _I$
that
 $$\begin{align*}\pi_i\cdot c_D\varepsilon_I=\begin{cases} -c_D\varepsilon_I & \mbox{ if } i\in I \\ 0 & \mbox{ if } i\not\in I. \end{cases}\end{align*}$$
$$\begin{align*}\pi_i\cdot c_D\varepsilon_I=\begin{cases} -c_D\varepsilon_I & \mbox{ if } i\in I \\ 0 & \mbox{ if } i\not\in I. \end{cases}\end{align*}$$
Extending by linearity, we find that
![]() $f_c\in \mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
whenever
$f_c\in \mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
whenever
![]() $c\in Cl_V$
.
$c\in Cl_V$
.
To prove the converse, suppose
![]() $c\not \in Cl_V$
. Let
$c\not \in Cl_V$
. Let
![]() $c_D\varepsilon _I$
be a term in the support of
$c_D\varepsilon _I$
be a term in the support of
![]() $c\,\varepsilon _I$
such that
$c\,\varepsilon _I$
such that
![]() $D\not \subseteq V$
; we may assume that this term is chosen maximally with respect to the partial order
$D\not \subseteq V$
; we may assume that this term is chosen maximally with respect to the partial order
![]() $\leq _I$
. Because
$\leq _I$
. Because
![]() $D\not \subseteq V$
, there exists i such that either
$D\not \subseteq V$
, there exists i such that either
![]() $i\in I$
and
$i\in I$
and
![]() $i+1\in D$
or
$i+1\in D$
or
![]() $i\not \in I$
and
$i\not \in I$
and
![]() $i\in D$
. Then either
$i\in D$
. Then either
![]() $i\in I$
and
$i\in I$
and
![]() $\alpha (i,I,D)=0$
or
$\alpha (i,I,D)=0$
or
![]() $i\not \in I$
and
$i\not \in I$
and
![]() $\alpha (i,I,D)=-1$
. Combining Lemma 5.1 with the
$\alpha (i,I,D)=-1$
. Combining Lemma 5.1 with the
![]() $\leq _I$
-maximality of
$\leq _I$
-maximality of
![]() $c_D\varepsilon _I$
, we find that (5.2) does not hold; thus,
$c_D\varepsilon _I$
, we find that (5.2) does not hold; thus,
![]() $f_c\not \in \mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
.
$f_c\not \in \mathrm {End}_{HCl_n^B(0)}(\mathcal M_I)$
.
We now proceed to characterize when two
![]() $HCl_n^B(0)$
-modules
$HCl_n^B(0)$
-modules
![]() $\mathcal M_I$
and
$\mathcal M_I$
and
![]() $\mathcal M_J$
are isomorphic.
$\mathcal M_J$
are isomorphic.
Theorem 5.5 Let
![]() $I,J\subseteq [0,n-1]$
. The
$I,J\subseteq [0,n-1]$
. The
![]() $HCl_n^B(0)$
-modules
$HCl_n^B(0)$
-modules
![]() $\mathcal M_I$
and
$\mathcal M_I$
and
![]() $\mathcal M_J$
are isomorphic if and only if
$\mathcal M_J$
are isomorphic if and only if
Proof If
![]() $\mathcal M_I$
and
$\mathcal M_I$
and
![]() $\mathcal M_J$
are isomorphic, then
$\mathcal M_J$
are isomorphic, then
![]() $\mathrm {ch}^B(\mathrm {Res}_{H_n^B(0)}(\mathcal M_I))=\mathrm {ch}^B(\mathrm {Res}_{H_n^B(0)}(\mathcal M_J))$
, so it follows from Theorem 5.3 that
$\mathrm {ch}^B(\mathrm {Res}_{H_n^B(0)}(\mathcal M_I))=\mathrm {ch}^B(\mathrm {Res}_{H_n^B(0)}(\mathcal M_J))$
, so it follows from Theorem 5.3 that
![]() $\mathrm {Peak}^B([0,n-1]\setminus I)=\mathrm {Peak}^B([0,n-1]\setminus J)$
and
$\mathrm {Peak}^B([0,n-1]\setminus I)=\mathrm {Peak}^B([0,n-1]\setminus J)$
and
![]() $0\not \in I\triangle J$
.
$0\not \in I\triangle J$
.
To prove the converse, it suffices to prove that
![]() $\mathcal M_I\cong \mathcal M_J$
whenever the following hold:
$\mathcal M_I\cong \mathcal M_J$
whenever the following hold:
-
•
 $\mathrm {Peak}^B([0,n-1]\setminus I)=\mathrm {Peak}^B([0,n-1]\setminus J)$
;
$\mathrm {Peak}^B([0,n-1]\setminus I)=\mathrm {Peak}^B([0,n-1]\setminus J)$
; -
•
 $0\notin I\triangle J$
;
$0\notin I\triangle J$
; -
•
 $J=I\sqcup \{k\}$
for some
$J=I\sqcup \{k\}$
for some
 $k\in [n-1]\setminus I$
.
$k\in [n-1]\setminus I$
.
Note that if
![]() $k+1\in I\cap J$
, then
$k+1\in I\cap J$
, then
![]() $k+1$
is in
$k+1$
is in
![]() $\mathrm {Peak}^B([0,n-1]\setminus J)$
but not in
$\mathrm {Peak}^B([0,n-1]\setminus J)$
but not in
![]() $\mathrm {Peak}^B([0,n-1]\setminus I)$
, which is impossible. Thus,
$\mathrm {Peak}^B([0,n-1]\setminus I)$
, which is impossible. Thus,
![]() $k+1\notin I\cap J$
. Similarly, if
$k+1\notin I\cap J$
. Similarly, if
![]() $k-1\in I\cup J$
, then k is in
$k-1\in I\cup J$
, then k is in
![]() $\mathrm {Peak}^B([0,n-1]\setminus I)$
but not in
$\mathrm {Peak}^B([0,n-1]\setminus I)$
but not in
![]() $\mathrm {Peak}^B([0,n-1]\setminus J)$
, which is impossible. Thus,
$\mathrm {Peak}^B([0,n-1]\setminus J)$
, which is impossible. Thus,
![]() $k-1\not \in I\cup J$
. This implies that the pieces of the ribbon diagrams representing
$k-1\not \in I\cup J$
. This implies that the pieces of the ribbon diagrams representing
![]() $\varepsilon _I$
and
$\varepsilon _I$
and
![]() $\varepsilon _J$
near box k look like
$\varepsilon _J$
near box k look like

respectively.
Let
![]() $\eta =(c_kc_{k+1}-1)\varepsilon _J\in \mathcal M_J$
, and define a linear map
$\eta =(c_kc_{k+1}-1)\varepsilon _J\in \mathcal M_J$
, and define a linear map
![]() $f\colon \mathcal M_I\to \mathcal M_J$
by
$f\colon \mathcal M_I\to \mathcal M_J$
by
![]() $f(x\varepsilon _I)=x\eta $
for all
$f(x\varepsilon _I)=x\eta $
for all
![]() $x\in Cl_n$
. The map f is injective because
$x\in Cl_n$
. The map f is injective because
![]() $c_kc_{k-1}-1$
is invertible in
$c_kc_{k-1}-1$
is invertible in
![]() $Cl_n$
. Since
$Cl_n$
. Since
![]() $\mathcal M_I$
and
$\mathcal M_I$
and
![]() $\mathcal M_J$
have the same dimension, f is an isomorphism of
$\mathcal M_J$
have the same dimension, f is an isomorphism of
![]() $Cl_n$
-modules. To show that f is an isomorphism of
$Cl_n$
-modules. To show that f is an isomorphism of
![]() $HCl_n^B(0)$
-modules, we need to check that
$HCl_n^B(0)$
-modules, we need to check that
![]() $\pi _i\cdot \eta =f(\pi _i\cdot \varepsilon _I)$
for all
$\pi _i\cdot \eta =f(\pi _i\cdot \varepsilon _I)$
for all
![]() $i\in [0,n-1]$
. We consider several cases.
$i\in [0,n-1]$
. We consider several cases.
Suppose
![]() $i\notin \{k-1,k,k+1\}$
. Then
$i\notin \{k-1,k,k+1\}$
. Then
![]() $\pi _i$
commutes with
$\pi _i$
commutes with
![]() $c_kc_{k+1}-1$
, so
$c_kc_{k+1}-1$
, so
as desired.
Suppose
![]() $k=1$
and
$k=1$
and
![]() $i=0$
. Then
$i=0$
. Then
![]() $0\notin I\cup J$
, so
$0\notin I\cup J$
, so
as desired.
Suppose
![]() $k>1$
and
$k>1$
and
![]() $i=k-1$
. Then
$i=k-1$
. Then
![]() $k-1\notin I\cup J$
, so
$k-1\notin I\cup J$
, so
as desired.
Suppose
![]() $i=k$
. Then
$i=k$
. Then
 $$ \begin{align*} \pi_k\cdot\eta&=((c_{k+1}\pi_k+c_{k+1}-c_k)c_{k+1}-\pi_k)\cdot\varepsilon_J \\ &=(-c_kc_{k+1}\pi_k-1-c_kc_{k+1}-\pi_k)\cdot\varepsilon_J \\ &=-c_kc_{k+1}(-\varepsilon_J)-\varepsilon_J-c_kc_{k+1}\varepsilon_J-(-\varepsilon_J) \\ &=0 \\ &=f(\pi_k\cdot\varepsilon_I), \end{align*} $$
$$ \begin{align*} \pi_k\cdot\eta&=((c_{k+1}\pi_k+c_{k+1}-c_k)c_{k+1}-\pi_k)\cdot\varepsilon_J \\ &=(-c_kc_{k+1}\pi_k-1-c_kc_{k+1}-\pi_k)\cdot\varepsilon_J \\ &=-c_kc_{k+1}(-\varepsilon_J)-\varepsilon_J-c_kc_{k+1}\varepsilon_J-(-\varepsilon_J) \\ &=0 \\ &=f(\pi_k\cdot\varepsilon_I), \end{align*} $$
as desired.
Finally, suppose
![]() $i=k+1$
. Then
$i=k+1$
. Then
![]() $k+1\in I\cap J$
, so
$k+1\in I\cap J$
, so
 $$ \begin{align*} \pi_{k+1}\cdot\eta&=(c_k(c_{k+2}\pi_{k+1}+c_{k+2}-c_{k+1})-\pi_{k+1})\cdot\varepsilon_J \\ &=(c_kc_{k+2}\pi_{k+1}+c_kc_{k+2}-c_kc_{k+1}-\pi_{k+1})\cdot\varepsilon_J \\ &=c_kc_{k+2}(-\varepsilon_J)+c_kc_{k+2}\varepsilon_J-c_kc_{k+1}\varepsilon_J-(-\varepsilon_J) \\ &=-\eta \\ &=f(\pi_k\cdot \varepsilon_I), \end{align*} $$
$$ \begin{align*} \pi_{k+1}\cdot\eta&=(c_k(c_{k+2}\pi_{k+1}+c_{k+2}-c_{k+1})-\pi_{k+1})\cdot\varepsilon_J \\ &=(c_kc_{k+2}\pi_{k+1}+c_kc_{k+2}-c_kc_{k+1}-\pi_{k+1})\cdot\varepsilon_J \\ &=c_kc_{k+2}(-\varepsilon_J)+c_kc_{k+2}\varepsilon_J-c_kc_{k+1}\varepsilon_J-(-\varepsilon_J) \\ &=-\eta \\ &=f(\pi_k\cdot \varepsilon_I), \end{align*} $$
as desired.
It would be interesting to determine the simple
![]() $HCl_n^B(0)$
-modules. We note that the algebra
$HCl_n^B(0)$
-modules. We note that the algebra
![]() $HCl_n^B(0)$
is not a superalgebra and that the approach used in [Reference Bergeron, Hivert and Thibon3, Section 5.4] for the simple
$HCl_n^B(0)$
is not a superalgebra and that the approach used in [Reference Bergeron, Hivert and Thibon3, Section 5.4] for the simple
![]() $HCl_n(0)$
-modules does not carry over.
$HCl_n(0)$
-modules does not carry over.
6 Type-B quasisymmetric characteristics from
 $0$
-Hecke–Clifford modules
$0$
-Hecke–Clifford modules
In this section, we prove a result that allows us to compute the type-B quasisymmetric characteristic of
![]() $\mathrm {Res}_{H_n^B(0)}\left (\mathrm {Ind}_{H_n^B(0)}^{HCl_n^B(0)}(\textbf {N})\right )$
, where
$\mathrm {Res}_{H_n^B(0)}\left (\mathrm {Ind}_{H_n^B(0)}^{HCl_n^B(0)}(\textbf {N})\right )$
, where
![]() $\textbf {N}$
is an
$\textbf {N}$
is an
![]() $H_n^B(0)$
-module of a special form. In particular, we will see that one can apply this theorem when
$H_n^B(0)$
-module of a special form. In particular, we will see that one can apply this theorem when
![]() $\textbf {N}$
is a module obtained via the type-B ascent compatibility framework. As a different application, we will provide a representation–theoretic interpretation of the shifted domino functions
$\textbf {N}$
is a module obtained via the type-B ascent compatibility framework. As a different application, we will provide a representation–theoretic interpretation of the shifted domino functions
![]() $H_\lambda $
from Section 4.
$H_\lambda $
from Section 4.
Let
![]() $\mathscr X$
and
$\mathscr X$
and
![]() $\mathscr Y$
be finite sets with
$\mathscr Y$
be finite sets with
![]() $\mathscr X\subseteq \mathscr Y$
. Let
$\mathscr X\subseteq \mathscr Y$
. Let
![]() $\textbf {L}:\mathscr X\to 2^{[0,n-1]}$
be a function, where
$\textbf {L}:\mathscr X\to 2^{[0,n-1]}$
be a function, where
![]() $2^{[0,n-1]}$
is the power set of
$2^{[0,n-1]}$
is the power set of
![]() $[0,n-1]$
. Let
$[0,n-1]$
. Let
![]() $f_0,\ldots ,f_{n-1}:\mathscr X\to \mathscr Y$
be functions. Define linear operators
$f_0,\ldots ,f_{n-1}:\mathscr X\to \mathscr Y$
be functions. Define linear operators
![]() $\pi _0,\ldots ,\pi _{n-1}$
on
$\pi _0,\ldots ,\pi _{n-1}$
on
![]() $\mathbb C\mathscr X$
by letting
$\mathbb C\mathscr X$
by letting
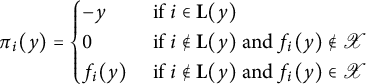 $$\begin{align*}\pi_i(y) = \begin{cases} -y & \mbox{ if } i\in\textbf{L}(y) \\ 0 & \mbox{ if } i\notin\textbf{L}(y)\mbox{ and }f_i(y)\notin \mathscr X \\ f_i(y) & \mbox{ if } i\notin\textbf{L}(y)\mbox{ and }f_i(y)\in \mathscr X \end{cases}\end{align*}$$
$$\begin{align*}\pi_i(y) = \begin{cases} -y & \mbox{ if } i\in\textbf{L}(y) \\ 0 & \mbox{ if } i\notin\textbf{L}(y)\mbox{ and }f_i(y)\notin \mathscr X \\ f_i(y) & \mbox{ if } i\notin\textbf{L}(y)\mbox{ and }f_i(y)\in \mathscr X \end{cases}\end{align*}$$
and extending by linearity. For
![]() $y,y'\in \mathscr X$
, let us write
$y,y'\in \mathscr X$
, let us write
![]() $y\preceq y'$
if there is a (possibly empty) sequence
$y\preceq y'$
if there is a (possibly empty) sequence
![]() $i_1,\ldots ,i_r$
of indices in
$i_1,\ldots ,i_r$
of indices in
![]() $[0,n-1]$
such that
$[0,n-1]$
such that
![]() $y'=\pi _{i_r}\dots \pi _{i_1}(y)$
.
$y'=\pi _{i_r}\dots \pi _{i_1}(y)$
.
Theorem 6.1 Suppose the operators
![]() $\pi _0,\ldots ,\pi _{n-1}$
define an action of
$\pi _0,\ldots ,\pi _{n-1}$
define an action of
![]() $H_n^B(0)$
on
$H_n^B(0)$
on
![]() $\mathbb C\mathscr X$
. If the relation
$\mathbb C\mathscr X$
. If the relation
![]() $\preceq $
is a partial order, then
$\preceq $
is a partial order, then
 $$\begin{align*}\mathrm{ch}^B\left(\mathrm{Res}_{H_n^B(0)}\left(\mathrm{Ind}_{H_n^B(0)}^{HCl_n^B(0)}(\mathbb C\mathscr X)\right)\right)=\sum_{y\in \mathscr X}\Delta^B([0,n-1]\setminus\textbf{L}(y)).\end{align*}$$
$$\begin{align*}\mathrm{ch}^B\left(\mathrm{Res}_{H_n^B(0)}\left(\mathrm{Ind}_{H_n^B(0)}^{HCl_n^B(0)}(\mathbb C\mathscr X)\right)\right)=\sum_{y\in \mathscr X}\Delta^B([0,n-1]\setminus\textbf{L}(y)).\end{align*}$$
Proof A linear basis of
![]() $\mathrm {Ind}_{H_n^B(0)}^{HCl_n^B(0)}(\mathbb C\mathscr X)$
is
$\mathrm {Ind}_{H_n^B(0)}^{HCl_n^B(0)}(\mathbb C\mathscr X)$
is
![]() $\{c_Dy:D\subseteq [0,n-1],\, y\in \mathscr X\}$
. Let
$\{c_Dy:D\subseteq [0,n-1],\, y\in \mathscr X\}$
. Let
![]() $y_1,\ldots ,y_m$
be a linear extension of the poset
$y_1,\ldots ,y_m$
be a linear extension of the poset
![]() $(\mathscr X,\preceq )$
. For
$(\mathscr X,\preceq )$
. For
![]() $0\leq k\leq m$
, let
$0\leq k\leq m$
, let
![]() $\widetilde {\textbf {N}}_k=\text {span}\{c_Dy_j:D\subseteq [0,n-1],\, j\leq k\}$
; then
$\widetilde {\textbf {N}}_k=\text {span}\{c_Dy_j:D\subseteq [0,n-1],\, j\leq k\}$
; then
![]() $\widetilde {\textbf {N}}_k$
is an
$\widetilde {\textbf {N}}_k$
is an
![]() $HCl_n^B(0)$
-module because
$HCl_n^B(0)$
-module because
![]() $\preceq $
is a partial order. For
$\preceq $
is a partial order. For
![]() $1\leq k\leq m$
, a linear basis for the quotient module
$1\leq k\leq m$
, a linear basis for the quotient module
![]() $\widetilde {\textbf {N}}_k/\widetilde {\textbf {N}}_{k-1}$
is
$\widetilde {\textbf {N}}_k/\widetilde {\textbf {N}}_{k-1}$
is
![]() $\{c_D\overline y_k:D\subseteq [0,n-1]\}$
, where
$\{c_D\overline y_k:D\subseteq [0,n-1]\}$
, where
![]() $\overline y_k=y_k+\widetilde {\textbf {N}}_{k-1}$
. We have
$\overline y_k=y_k+\widetilde {\textbf {N}}_{k-1}$
. We have
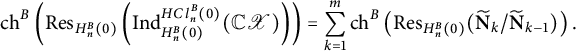 $$\begin{align*}\mathrm{ch}^B\left(\mathrm{Res}_{H_n^B(0)}\left(\mathrm{Ind}_{H_n^B(0)}^{HCl_n^B(0)}(\mathbb C\mathscr X)\right)\right)=\sum_{k=1}^m\mathrm{ch}^B\left(\mathrm{Res}_{H_n^B(0)}(\widetilde{\textbf{N}}_k/\widetilde{\textbf{N}}_{k-1})\right).\end{align*}$$
$$\begin{align*}\mathrm{ch}^B\left(\mathrm{Res}_{H_n^B(0)}\left(\mathrm{Ind}_{H_n^B(0)}^{HCl_n^B(0)}(\mathbb C\mathscr X)\right)\right)=\sum_{k=1}^m\mathrm{ch}^B\left(\mathrm{Res}_{H_n^B(0)}(\widetilde{\textbf{N}}_k/\widetilde{\textbf{N}}_{k-1})\right).\end{align*}$$
Hence, the desired result will follow from Theorem 5.3 if we can prove that the
![]() $HCl_n^B(0)$
-module
$HCl_n^B(0)$
-module
![]() $\widetilde {\textbf {N}}_k/\widetilde {\textbf {N}}_{k-1}$
is isomorphic to
$\widetilde {\textbf {N}}_k/\widetilde {\textbf {N}}_{k-1}$
is isomorphic to
![]() $\mathcal M_{\textbf {L}(y_k)}$
.
$\mathcal M_{\textbf {L}(y_k)}$
.
Define a map
![]() $\psi \colon \widetilde {\textbf {N}}_k/\widetilde {\textbf {N}}_{k-1}\to \mathcal M_{\textbf {L}(y_k)}$
by letting
$\psi \colon \widetilde {\textbf {N}}_k/\widetilde {\textbf {N}}_{k-1}\to \mathcal M_{\textbf {L}(y_k)}$
by letting
![]() $\psi (c_D\overline y_k)=c_D\varepsilon _{\textbf {L}(y_k)}$
and extending by linearity. Then
$\psi (c_D\overline y_k)=c_D\varepsilon _{\textbf {L}(y_k)}$
and extending by linearity. Then
![]() $\psi $
is clearly a linear isomorphism, so we just need to show that it respects the module structure. For
$\psi $
is clearly a linear isomorphism, so we just need to show that it respects the module structure. For
![]() $r\in [n]$
and
$r\in [n]$
and
![]() $D\subseteq [n]$
, let
$D\subseteq [n]$
, let
![]() $p_r(D)=|[r]\cap D|$
. We have
$p_r(D)=|[r]\cap D|$
. We have
 $$ \begin{align*} c_r\psi(c_D\overline y_k)&=c_rc_D\varepsilon_{\textbf{L}(y_k)} \\ &=(-1)^{p_r(D)}c_{D\triangle\{r\}}\varepsilon_{\textbf{L}(y_k)} \\ &=\psi((-1)^{p_r(D)}c_{D\triangle\{r\}}\overline y_k) \\ &=\psi(c_rc_D\overline y_k). \end{align*} $$
$$ \begin{align*} c_r\psi(c_D\overline y_k)&=c_rc_D\varepsilon_{\textbf{L}(y_k)} \\ &=(-1)^{p_r(D)}c_{D\triangle\{r\}}\varepsilon_{\textbf{L}(y_k)} \\ &=\psi((-1)^{p_r(D)}c_{D\triangle\{r\}}\overline y_k) \\ &=\psi(c_rc_D\overline y_k). \end{align*} $$
This shows that
![]() $\psi $
commutes with the action of the generators
$\psi $
commutes with the action of the generators
![]() $c_1,\ldots ,c_n$
.
$c_1,\ldots ,c_n$
.
To complete the proof, we must show that
![]() $\pi _i\psi (c_D\overline y_k)=\psi (\pi _ic_D\overline y_k)$
for all
$\pi _i\psi (c_D\overline y_k)=\psi (\pi _ic_D\overline y_k)$
for all
![]() ${i\in [0,n-1]}$
and
${i\in [0,n-1]}$
and
![]() $D\subseteq [n]$
. Fix such an index i and a subset D. Using the defining relations of
$D\subseteq [n]$
. Fix such an index i and a subset D. Using the defining relations of
![]() $HCl_n^B(0)$
, we can write
$HCl_n^B(0)$
, we can write
![]() $\pi _ic_D$
in the form
$\pi _ic_D$
in the form
![]() $\sum _{E\subseteq [n]}c_E(\gamma _E+\delta _E\pi _i)$
, where
$\sum _{E\subseteq [n]}c_E(\gamma _E+\delta _E\pi _i)$
, where
![]() $\gamma _E,\delta _E\in \mathbb C$
for each
$\gamma _E,\delta _E\in \mathbb C$
for each
![]() $E\subseteq [n]$
. If
$E\subseteq [n]$
. If
![]() $i\in \textbf {L}(y_k)$
, then we have
$i\in \textbf {L}(y_k)$
, then we have
![]() $\pi _i\varepsilon _{\textbf {L}(y_k)}=-\varepsilon _{\textbf {L}(y_k)}=\psi (-\overline y_k)=\psi (\pi _i\overline y_k)$
. If
$\pi _i\varepsilon _{\textbf {L}(y_k)}=-\varepsilon _{\textbf {L}(y_k)}=\psi (-\overline y_k)=\psi (\pi _i\overline y_k)$
. If
![]() $i\not \in \textbf {L}(y_k)$
, then
$i\not \in \textbf {L}(y_k)$
, then
![]() $\pi _i\varepsilon _{\textbf {L}(y_k)}=0$
, and it follows from the definition of the partial order
$\pi _i\varepsilon _{\textbf {L}(y_k)}=0$
, and it follows from the definition of the partial order
![]() $\preceq $
that
$\preceq $
that
![]() $\pi _iy_k\in \text {span}\{y_1,\ldots ,y_{k-1}\}$
so that
$\pi _iy_k\in \text {span}\{y_1,\ldots ,y_{k-1}\}$
so that
![]() $\pi _i\overline y_k$
is
$\pi _i\overline y_k$
is
![]() $0$
in
$0$
in
![]() $\widetilde {\textbf {N}}_k/\widetilde {\textbf {N}}_{k-1}$
. In either case, we have
$\widetilde {\textbf {N}}_k/\widetilde {\textbf {N}}_{k-1}$
. In either case, we have
![]() $\pi _i\varepsilon _{\textbf {L}(y_k)}=\psi (\pi _i\overline y_k)$
. Hence, for each
$\pi _i\varepsilon _{\textbf {L}(y_k)}=\psi (\pi _i\overline y_k)$
. Hence, for each
![]() $E\subseteq [n]$
, we have
$E\subseteq [n]$
, we have
![]() $c_E(\gamma _E+\delta _E\pi _i)\varepsilon _{\textbf {L}(y_k)}=\psi (c_E(\gamma _E+\delta _E\pi _i)\overline y_k)$
. Thus,
$c_E(\gamma _E+\delta _E\pi _i)\varepsilon _{\textbf {L}(y_k)}=\psi (c_E(\gamma _E+\delta _E\pi _i)\overline y_k)$
. Thus,
 $$ \begin{align*} \pi_i\psi(c_D\overline y_k)&=\pi_ic_D\varepsilon_{\textbf{L}(y_k)} \\ &=\left(\sum_{E\subseteq[n]}c_E(\gamma_E+\delta_E\pi_i)\right)\varepsilon_{\textbf{L}(y_k)} \\ &=\psi\left(\left(\sum_{E\subseteq[n]}c_E(\gamma_E+\delta_E\pi_i)\right)\overline y_k\right) \\ &=\psi(\pi_ic_D\overline y_k), \end{align*} $$
$$ \begin{align*} \pi_i\psi(c_D\overline y_k)&=\pi_ic_D\varepsilon_{\textbf{L}(y_k)} \\ &=\left(\sum_{E\subseteq[n]}c_E(\gamma_E+\delta_E\pi_i)\right)\varepsilon_{\textbf{L}(y_k)} \\ &=\psi\left(\left(\sum_{E\subseteq[n]}c_E(\gamma_E+\delta_E\pi_i)\right)\overline y_k\right) \\ &=\psi(\pi_ic_D\overline y_k), \end{align*} $$
as desired.
Corollary 6.2 Let X be an ascent-compatible subset of
![]() $B_n$
, and let
$B_n$
, and let
![]() $\mathbb CX$
be the associated
$\mathbb CX$
be the associated
![]() $H_n^B(0)$
-module. Then
$H_n^B(0)$
-module. Then
Proof Apply Theorem 6.1 with
![]() $\mathscr X=X$
,
$\mathscr X=X$
,
![]() $\mathscr Y=B_n$
,
$\mathscr Y=B_n$
,
![]() $f_i(x)=s_ix$
, and
$f_i(x)=s_ix$
, and
![]() $\textbf {L}(x)=\mathrm {Des}(x)$
.
$\textbf {L}(x)=\mathrm {Des}(x)$
.
Let
![]() $\lambda $
be a pavable partition and let
$\lambda $
be a pavable partition and let
![]() $\widehat \lambda $
denote the conjugate of
$\widehat \lambda $
denote the conjugate of
![]() $\lambda $
. Recall from Section 4.2 the definition of the set
$\lambda $
. Recall from Section 4.2 the definition of the set
![]() $\mathsf {SShDT}(\lambda )$
of standard shifted domino tableaux of shape
$\mathsf {SShDT}(\lambda )$
of standard shifted domino tableaux of shape
![]() $\lambda $
. If we reflect a standard shifted domino tableau Q of shape
$\lambda $
. If we reflect a standard shifted domino tableau Q of shape
![]() $\lambda $
across the main diagonal, we obtain a filled tiling
$\lambda $
across the main diagonal, we obtain a filled tiling
![]() $\widehat Q$
of
$\widehat Q$
of
![]() $\widehat \lambda $
that we call a
$\widehat \lambda $
that we call a ![]() of shape
of shape
![]() $\widehat \lambda $
. See Figure 3 for an example. Let
$\widehat \lambda $
. See Figure 3 for an example. Let
![]() $\widehat {\mathsf {SShDT}}(\widehat \lambda )$
denote the set of conjugated standard shifted domino tableaux of shape
$\widehat {\mathsf {SShDT}}(\widehat \lambda )$
denote the set of conjugated standard shifted domino tableaux of shape
![]() $\widehat \lambda $
.
$\widehat \lambda $
.
Figure 3: A standard shifted domino tableau Q of shape
![]() $\lambda =(7,7,6,5,1)$
(left) and its corresponding conjugated standard shifted domino tableau
$\lambda =(7,7,6,5,1)$
(left) and its corresponding conjugated standard shifted domino tableau
![]() $\widehat Q$
of shape
$\widehat Q$
of shape
![]() ${\widehat \lambda =(5,4,4,4,4,3,2)}$
(right).
${\widehat \lambda =(5,4,4,4,4,3,2)}$
(right).
Descents of conjugated standard shifted domino tableaux are defined just as for standard shifted domino tableaux. Let
![]() $\widehat Q\in \widehat {\mathsf {SShDT}}(\widehat \lambda )$
, and let m be the number of dominoes weakly below the main diagonal in
$\widehat Q\in \widehat {\mathsf {SShDT}}(\widehat \lambda )$
, and let m be the number of dominoes weakly below the main diagonal in
![]() $\widehat Q$
. We say
$\widehat Q$
. We say
![]() $i\in [0,m-1]$
is a
$i\in [0,m-1]$
is a ![]() of
of
![]() $\widehat Q$
if
$\widehat Q$
if
![]() $i=0$
and the domino in
$i=0$
and the domino in
![]() $\widehat Q$
containing
$\widehat Q$
containing
![]() $1$
is vertical or if
$1$
is vertical or if
![]() $i>0$
and the domino in
$i>0$
and the domino in
![]() $\widehat Q$
containing
$\widehat Q$
containing
![]() $i+1$
is strictly lower than the domino in
$i+1$
is strictly lower than the domino in
![]() $\widehat Q$
containing i. Let
$\widehat Q$
containing i. Let
![]() $\mathrm {Des}(\widehat Q)$
be the set of descents of
$\mathrm {Des}(\widehat Q)$
be the set of descents of
![]() $\widehat Q$
. Note that if
$\widehat Q$
. Note that if
![]() $\widehat Q$
is the conjugate of the standard shifted domino tableau
$\widehat Q$
is the conjugate of the standard shifted domino tableau
![]() $Q\in \mathsf {SShDT}(\lambda )$
, then
$Q\in \mathsf {SShDT}(\lambda )$
, then
![]() $\mathrm {Des}(\widehat Q)=[0,n-1]\setminus \mathrm {Des}(Q)$
.
$\mathrm {Des}(\widehat Q)=[0,n-1]\setminus \mathrm {Des}(Q)$
.
For
![]() $0\leq i\leq n-1$
and
$0\leq i\leq n-1$
and
![]() $Q\in \mathsf {SShDT}(\lambda )$
, let
$Q\in \mathsf {SShDT}(\lambda )$
, let
![]() $s_i(\widehat Q)=\widehat {s_i(Q)}$
. Define operators
$s_i(\widehat Q)=\widehat {s_i(Q)}$
. Define operators
![]() $\pi _0, \pi _1, \ldots \pi _{n-1}$
on
$\pi _0, \pi _1, \ldots \pi _{n-1}$
on
![]() $\mathbb C\widehat {\mathsf {SShDT}}(\widehat \lambda )$
by
$\mathbb C\widehat {\mathsf {SShDT}}(\widehat \lambda )$
by
 $$\begin{align*}\pi_i(\widehat Q) = \begin{cases} -\widehat Q & \mbox{ if } i\in\mathrm{Des}(\widehat Q) \\ 0 & \mbox{ if } i\notin\mathrm{Des}(\widehat Q)\mbox{ and }s_i(\widehat Q)\notin\widehat{\mathsf{SShDT}}(\widehat\lambda) \\ s_i(\widehat Q) & \mbox{ if } i\notin\mathrm{Des}(\widehat Q)\mbox{ and }s_i(\widehat Q)\in\widehat{\mathsf{SShDT}}(\widehat\lambda) \end{cases}\end{align*}$$
$$\begin{align*}\pi_i(\widehat Q) = \begin{cases} -\widehat Q & \mbox{ if } i\in\mathrm{Des}(\widehat Q) \\ 0 & \mbox{ if } i\notin\mathrm{Des}(\widehat Q)\mbox{ and }s_i(\widehat Q)\notin\widehat{\mathsf{SShDT}}(\widehat\lambda) \\ s_i(\widehat Q) & \mbox{ if } i\notin\mathrm{Des}(\widehat Q)\mbox{ and }s_i(\widehat Q)\in\widehat{\mathsf{SShDT}}(\widehat\lambda) \end{cases}\end{align*}$$
for each
![]() $Q\in \mathsf {SShDT}(\lambda )$
.
$Q\in \mathsf {SShDT}(\lambda )$
.
Theorem 6.3 Let
![]() $\lambda $
be a pavable partition. The operators
$\lambda $
be a pavable partition. The operators
![]() $\pi _0, \pi _1, \ldots , \pi _{n-1}$
define an action of
$\pi _0, \pi _1, \ldots , \pi _{n-1}$
define an action of
![]() $H_n^B(0)$
on
$H_n^B(0)$
on
![]() $\mathbb C\widehat {\mathsf {SShDT}}(\widehat \lambda )$
. Moreover,
$\mathbb C\widehat {\mathsf {SShDT}}(\widehat \lambda )$
. Moreover,
Proof The proof that
![]() $\pi _0, \pi _1, \ldots , \pi _{n-1}$
define an action of
$\pi _0, \pi _1, \ldots , \pi _{n-1}$
define an action of
![]() $H_n^B(0)$
is very similar to that of Theorem 4.2, so we omit it. To prove the desired identity involving the shifted domino function
$H_n^B(0)$
is very similar to that of Theorem 4.2, so we omit it. To prove the desired identity involving the shifted domino function
![]() $H_\lambda $
, we appeal to Theorem 6.1. Let
$H_\lambda $
, we appeal to Theorem 6.1. Let
![]() $\mathscr X=\widehat {\mathsf {SShDT}}(\widehat \lambda )$
and
$\mathscr X=\widehat {\mathsf {SShDT}}(\widehat \lambda )$
and
![]() ${\mathscr Y=\widehat {\mathsf {SShDT}}(\widehat \lambda )\cup \{\bullet \}}$
, where
${\mathscr Y=\widehat {\mathsf {SShDT}}(\widehat \lambda )\cup \{\bullet \}}$
, where
![]() $\bullet $
is a formal symbol. For
$\bullet $
is a formal symbol. For
![]() $0\leq i\leq n-1$
, define
$0\leq i\leq n-1$
, define
![]() $f_i\colon \mathscr X\to \mathscr Y$
by
$f_i\colon \mathscr X\to \mathscr Y$
by
 $$\begin{align*}f_i(\widehat Q)=\begin{cases} s_i(\widehat Q) & \mbox{ if } s_i(\widehat Q)\in\widehat{\mathsf{SShDT}}(\widehat\lambda) \\ \bullet & \mbox{ if } s_i(\widehat Q)\notin\widehat{\mathsf{SShDT}}(\widehat\lambda). \end{cases}\end{align*}$$
$$\begin{align*}f_i(\widehat Q)=\begin{cases} s_i(\widehat Q) & \mbox{ if } s_i(\widehat Q)\in\widehat{\mathsf{SShDT}}(\widehat\lambda) \\ \bullet & \mbox{ if } s_i(\widehat Q)\notin\widehat{\mathsf{SShDT}}(\widehat\lambda). \end{cases}\end{align*}$$
Finally, let us define
![]() $\textbf {L}\colon \mathscr X\to 2^{[0,n-1]}$
by
$\textbf {L}\colon \mathscr X\to 2^{[0,n-1]}$
by
![]() $\textbf {L}(\widehat Q)=\mathrm {Des}(\widehat Q)$
. The desired result now follows from Corollary 4.8, Theorem 6.1, and the observation that
$\textbf {L}(\widehat Q)=\mathrm {Des}(\widehat Q)$
. The desired result now follows from Corollary 4.8, Theorem 6.1, and the observation that
![]() $\mathrm {Des}(\widehat Q)=[0,n-1]\setminus\mathrm {Des}(Q)$
for each
$\mathrm {Des}(\widehat Q)=[0,n-1]\setminus\mathrm {Des}(Q)$
for each
![]() ${Q\in \mathsf {SShDT}(\lambda )}$
.
${Q\in \mathsf {SShDT}(\lambda )}$
.
Acknowledgements
We thank the anonymous referee for helpful comments.



















