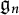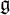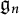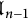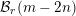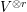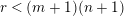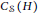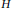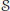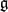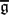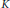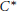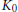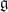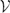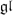Refine search
Actions for selected content:
44 results
Correction to “Irreducible modules of modular Lie superalgebras and super version of the first Kac-Weisfeiler conjecture”
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
 $\mathbf {5 \times 5}$-graded Lie algebras, cubic norm structures and quadrangular algebras
$\mathbf {5 \times 5}$-graded Lie algebras, cubic norm structures and quadrangular algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Biderivations of Lie algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 440-450
- Print publication:
- June 2025
-
- Article
- Export citation
Irreducible modules of modular Lie superalgebras and super version of the first Kac–Weisfeiler conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 554-573
- Print publication:
- September 2024
-
- Article
- Export citation
The Frobenius semiradical, generic stabilizers, and Poisson center for nilradicals
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 2019-2048
- Print publication:
- December 2024
-
- Article
- Export citation
Category
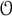 $\mathcal {O}$ for truncated current Lie algebras
$\mathcal {O}$ for truncated current Lie algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 19 October 2023, pp. 1795-1821
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of simple Harish–Chandra modules over the Ovsienko–Roger superalgebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 14 March 2023, pp. 483-493
- Print publication:
- April 2024
-
- Article
- Export citation
Symmetrisation and the Feigin–Frenkel centre
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 19 May 2022, pp. 585-622
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mirabolic Satake equivalence and supergroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 22 July 2021, pp. 1724-1765
- Print publication:
- August 2021
-
- Article
- Export citation
THE SECOND FUNDAMENTAL THEOREM OF INVARIANT THEORY FOR THE ORTHOSYMPLECTIC SUPERGROUP
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 04 December 2019, pp. 52-76
- Print publication:
- June 2021
-
- Article
- Export citation
PARABOLIC SUBROOT SYSTEMS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 30 April 2019, pp. 355-366
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
Classification of Simple Weight Modules over the Schrödinger Algebra
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 16-39
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
THE GROUP OF AUTOMORPHISMS OF THE LIE ALGEBRA OF DERIVATIONS OF A FIELD OF RATIONAL FUNCTIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 513-524
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
ISOMORPHIC INDUCED MODULES AND DYNKIN DIAGRAM AUTOMORPHISMS OF SEMISIMPLE LIE ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 187-203
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
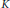 $K$ -theory of Furstenberg Transformation Group
$K$ -theory of Furstenberg Transformation Group 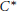 ${{\text{C}}^{\text{*}}}$ -algebras
${{\text{C}}^{\text{*}}}$ -algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 6 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1287-1319
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
Characterization of Simple Highest Weight Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 606-614
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
IRREDUCIBLE HARISH CHANDRA MODULES OVER THE DERIVATION ALGEBRAS OF RATIONAL QUANTUM TORI
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 677-693
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Left Invariant Einstein–Randers Metrics on Compact Lie Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 870-881
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
Classification of irreducible Harish-Chandra modules over generalized Virasoro algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 697-709
-
- Article
-
- You have access
- Export citation
Erratum: Cartan Subalgebras of gl∞
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 3 / 01 September 2011
- Published online by Cambridge University Press:
- 20 November 2018, p. 519
- Print publication:
- 01 September 2011
-
- Article
-
- You have access
- Export citation


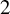

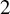
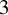




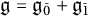
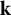
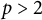
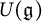
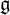
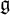
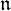
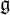
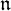
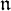
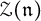 of the symmetric algebra
of the symmetric algebra 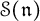 ,
, 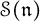 as
as 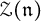 -module, and
-module, and