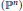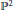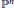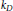Refine search
Actions for selected content:
12 results
ON THE MILNOR FIBRATION OF CERTAIN NEWTON DEGENERATE FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 410-433
- Print publication:
- June 2023
-
- Article
- Export citation
SYMBOLIC ANALYTIC SPREAD: UPPER BOUNDS AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 07 May 2020, pp. 1969-1981
- Print publication:
- November 2021
-
- Article
- Export citation
Subcategories of singularity categories via tensor actions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 2 / February 2014
- Published online by Cambridge University Press:
- 22 November 2013, pp. 229-272
- Print publication:
- February 2014
-
- Article
- Export citation
Hyperbolicity related problems for complete intersection varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 18 November 2013, pp. 369-395
- Print publication:
- March 2014
-
- Article
- Export citation
Corrigendum: Varieties with ample cotangent bundle (Compositio Math. 141 (2005), 1445–1459)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 505-506
- Print publication:
- March 2013
-
- Article
- Export citation
A generalized Gaeta’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 689-704
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
A unified formula for Steenrod operations in flag manifolds
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 19 January 2007, pp. 257-270
- Print publication:
- January 2007
-
- Article
-
- You have access
- Export citation
Varieties with ample cotangent bundle
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 6 / November 2005
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1445-1459
- Print publication:
- November 2005
-
- Article
-
- You have access
- Export citation
Generalized k-Configurations
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 2 / 01 April 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 400-415
- Print publication:
- 01 April 2005
-
- Article
-
- You have access
- Export citation
Decompositions of the Hilbert Function of a Set of Points in ℙn
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 5 / 01 October 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 923-943
- Print publication:
- 01 October 2001
-
- Article
-
- You have access
- Export citation
The Conductor of Points Having the Hilbert Function of a Complete Intersection in P 2
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 1 / 01 December 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 167-179
- Print publication:
- 01 December 1991
-
- Article
-
- You have access
- Export citation
On Complete Intersections Over an Algebraically Non-Closed Field
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 2 / 01 June 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 140-145
- Print publication:
- 01 June 1986
-
- Article
-
- You have access
- Export citation