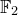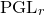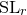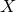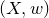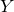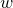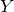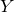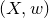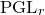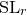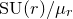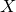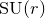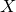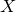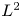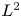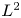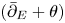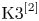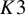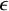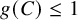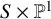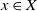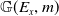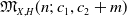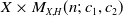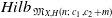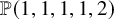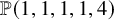Refine search
Actions for selected content:
41 results
Equivariant Segre and Verlinde invariants for Quot schemes
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXCEPTIONAL PAIRS ON DEL PEZZO SURFACES AND SPACES OF COMPATIBLE FEIGIN-ODESSKII BRACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-35
-
- Article
- Export citation
Free summands of stably free modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 May 2025, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal real varieties from moduli constructions
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A virtual
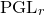 ${\rm PGL}_r$–
${\rm PGL}_r$–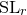 ${\rm SL}_r$ correspondence for projective surfaces
${\rm SL}_r$ correspondence for projective surfaces
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak stability conditions as limits of Bridgeland stability conditions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nef vector bundles on a quadric threefold with first Chern class two
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 526-565
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vanishing theorem for tame harmonic bundles via L2-cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 03 April 2025, pp. 2828-2855
- Print publication:
- December 2024
-
- Article
- Export citation
Towards a modular construction of OG10
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. 2496-2529
- Print publication:
- October 2024
-
- Article
- Export citation
Quasimaps to moduli spaces of sheaves on a
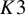 $K3$ surface
$K3$ surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 May 2024, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived Category and ACM Bundles of Moduli Space of Vector Bundles on a Curve
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 September 2023, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positive Ulrich sheaves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 April 2023, pp. 881-914
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Hilbert scheme of the moduli space of torsion-free sheaves on surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 02 February 2023, pp. 414-429
- Print publication:
- May 2023
-
- Article
- Export citation
Virasoro constraints for moduli spaces of sheaves on surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 January 2023, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived categories of hyper-Kähler manifolds: extended Mukai vector and integral structure
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 109-152
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability conditions on Calabi-Yau double/triple solids
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 August 2022, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON RANK TWO STABLE BUNDLES OVER SURFACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 28 June 2021, pp. 397-410
- Print publication:
- May 2022
-
- Article
- Export citation
Verlinde formulae on complex surfaces: K-theoretic invariants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e5
-
- Article
-
- You have access
- Open access
- Export citation
Instanton sheaves and representations of quivers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 984-1004
-
- Article
- Export citation
Degeneracy loci, virtual cycles and nested Hilbert schemes II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1623-1663
- Print publication:
- August 2020
-
- Article
- Export citation