Refine search
Actions for selected content:
33 results
Heights and quantitative arithmetic on stacky curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 January 2024, pp. 481-534
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERSECTING THE TORSION OF ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 56-63
- Print publication:
- August 2024
-
- Article
- Export citation
On the difference of two fourth powers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 142-150
-
- Article
- Export citation
Heights on stacks and a generalized Batyrev–Manin–Malle conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 March 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Faltings height and Néron–Tate height of a theta divisor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 1-32
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum: Generic rank of Betti map and unlikely intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 05 January 2022, pp. 2747-2748
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
Positivity of Hodge bundles of abelian varieties over some function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 03 August 2021, pp. 1964-2000
- Print publication:
- September 2021
-
- Article
- Export citation
Generic rank of Betti map and unlikely intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 12 January 2021, pp. 2469-2509
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
On intersections of polynomial semigroups orbits with plane lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 442-451
- Print publication:
- June 2021
-
- Article
- Export citation
A question for iterated Galois groups in arithmetic dynamics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 10 July 2020, pp. 401-417
- Print publication:
- June 2021
-
- Article
- Export citation
On the Frequency of Algebraic Brauer Classes on Certain Log K3 Surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 551-563
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Approximation forte pour les variétés avec une action d’un groupe linéaire
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 773-819
- Print publication:
- April 2018
-
- Article
- Export citation
ON PERFECT
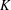 $K$ -RATIONAL CUBOIDS
$K$ -RATIONAL CUBOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 26-32
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
GENERALIZED EXPLICIT DESCENT AND ITS APPLICATION TO CURVES OF GENUS 3
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, e6
-
- Article
-
- You have access
- Open access
- Export citation
Arithmetic of positive characteristic
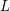 $L$-series values in Tate algebras
$L$-series values in Tate algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 1-61
- Print publication:
- January 2016
-
- Article
- Export citation
Computing Néron–Severi groups and cycle class groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 04 February 2015, pp. 713-734
- Print publication:
- April 2015
-
- Article
- Export citation
Computation of Mordell–Weil bases for ordinary elliptic curves in characteristic two
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 1-13
-
- Article
-
- You have access
- Export citation
Rational points on singular intersections of quadrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 20 June 2013, pp. 1457-1494
- Print publication:
- September 2013
-
- Article
- Export citation
On the Notion of Visibility of Torsors
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-228
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
Cycles de codimension 2 et H3 non ramifié pour les variétés sur les corps finis
-
- Journal:
- Journal of K-Theory / Volume 11 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 04 February 2013, pp. 1-53
- Print publication:
- February 2013
-
- Article
- Export citation
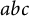
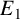
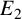
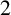
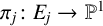
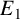
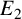
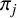
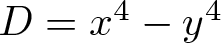
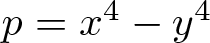
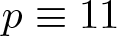
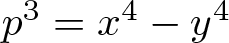
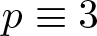
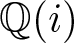
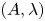
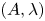
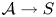
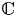
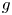

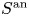
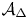
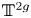
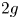
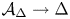
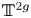
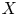
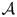
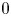
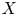
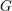
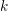
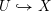
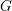
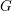
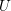
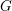
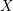
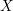
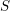
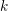
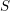
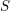
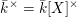
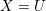
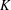
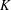
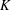
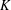
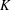
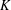
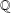
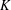
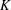
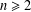

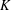
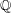
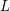
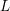
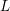
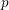
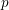
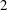
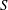
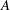
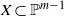
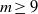
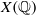
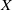
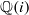
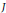
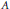
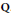
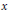
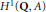
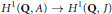
 . We discuss the unramified cohomology group
. We discuss the unramified cohomology group 