Refine search
Actions for selected content:
12 results
A VARIANT OF PERFECTOID ABHYANKAR’S LEMMA AND ALMOST COHEN–MACAULAY ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 164-215
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYTIC SPREAD OF FILTRATIONS ON TWO-DIMENSIONAL NORMAL LOCAL RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 239-268
- Print publication:
- March 2023
-
- Article
- Export citation
On Lipschitz normally embedded complex surface germs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 27 May 2022, pp. 623-653
- Print publication:
- March 2022
-
- Article
- Export citation
ON THE STRUCTURE OF GROUPS ENDOWED WITH A COMPATIBLE C-RELATION
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 23 October 2018, pp. 939-966
- Print publication:
- September 2018
-
- Article
- Export citation
Derivations and Valuation Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 31-38
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
RATLIFF–RUSH CLOSURE OF IDEALS IN INTEGRAL DOMAINS
-
- Journal:
- Glasgow Mathematical Journal / Volume 51 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 September 2009, pp. 681-689
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Radical Ideals in Valuation Domains
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 4 / 01 August 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 880-896
- Print publication:
- 01 August 2007
-
- Article
-
- You have access
- Export citation
Commutative rings with comparable regular elements
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-108
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
Valuation Rings and Integral Closure
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 3 / 01 September 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 327-330
- Print publication:
- 01 September 1990
-
- Article
-
- You have access
- Export citation
Integrally Closed Torsionless Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 31 / Issue 2 / 01 June 1988
- Published online by Cambridge University Press:
- 20 November 2018, pp. 215-216
- Print publication:
- 01 June 1988
-
- Article
-
- You have access
- Export citation
Torsion-free Abelian Groups, Valuations and Twisted Group Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 31 / Issue 2 / 01 June 1988
- Published online by Cambridge University Press:
- 20 November 2018, pp. 139-146
- Print publication:
- 01 June 1988
-
- Article
-
- You have access
- Export citation
Approximation Theorems for Manis Valuations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 2 / 01 June 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 184-189
- Print publication:
- 01 June 1985
-
- Article
-
- You have access
- Export citation
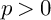
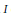
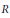
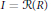
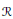
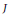
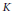
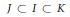
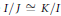
 be the class of commutative rings
be the class of commutative rings 