Refine search
Actions for selected content:
16 results
Abelian absolute Galois groups: In Erinnerung an Wulf-Dieter Geyer (1939–2019)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 02 February 2024, pp. 359-367
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decidability of the class of all the rings
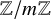 $\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
$\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE p-ZASSENHAUS FILTRATION OF A FREE PROFINITE GROUP AND SHUFFLE RELATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 961-983
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRIMITIVE RECURSIVE DECIDABILITY FOR THE RING OF INTEGERS OF THE COMPOSITUM OF ALL SYMMETRIC EXTENSIONS OF ℚ
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 08 May 2020, pp. 291-296
- Print publication:
- May 2021
-
- Article
- Export citation
LARGE FIELDS IN DIFFERENTIAL GALOIS THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 1931-1946
- Print publication:
- November 2021
-
- Article
- Export citation
EXTENSIONS OF HILBERTIAN RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 05 November 2018, pp. 1-11
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
STRONG APPROXIMATION THEOREM FOR ABSOLUTELY IRREDUCIBLE VARIETIES OVER THE COMPOSITUM OF ALL SYMMETRIC EXTENSIONS OF A GLOBAL FIELD
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 13 July 2018, pp. 373-380
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
TORSION OF ABELIAN VARIETIES OVER LARGE ALGEBRAIC EXTENSIONS OF
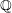 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 10 November 2017, pp. 46-86
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
DECIDABLE ALGEBRAIC FIELDS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. 474-488
- Print publication:
- June 2017
-
- Article
- Export citation
Defining Coarsenings of Valuations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 665-687
-
- Article
- Export citation
Vanishing of Massey Products and Brauer Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 4 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 730-740
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
DEFINABLE HENSELIAN VALUATIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 13 March 2015, pp. 85-99
- Print publication:
- March 2015
-
- Article
- Export citation
Produit eulérien motivique et courbes rationnelles sur les variétés toriques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1360-1400
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
The Absolute Galois Group of the Field of Totally S-Adic Numbers
-
- Journal:
- Nagoya Mathematical Journal / Volume 194 / 2009
- Published online by Cambridge University Press:
- 11 January 2016, pp. 91-147
- Print publication:
- 2009
-
- Article
-
- You have access
- Export citation
PROJECTIVE EXTENSIONS OF FIELDS
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 16 June 2006, pp. 639-656
- Print publication:
- June 2006
-
- Article
- Export citation
ELLIPTIC AND HYPERELLIPTIC CURVES OVER SUPERSIMPLE FIELDS
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 28 January 2004, pp. 1-13
- Print publication:
- February 2004
-
- Article
- Export citation
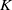

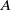
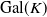
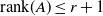
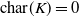
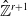
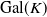
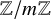
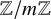
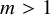
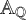

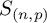
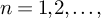
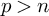
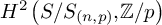
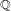
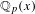
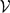
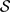
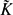
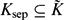
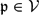
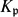
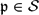
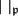
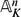
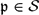
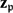
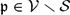
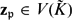
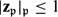
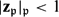
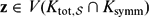
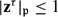
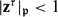
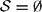
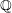
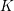
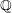
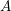
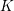
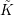
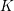
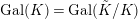
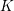
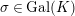
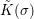

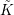
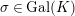
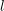
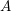
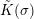
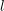
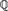
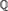
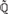
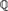
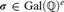
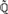
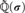
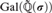
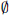 -definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.
-definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.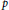

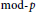
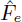 and a free product of local factors over
and a free product of local factors over 