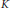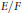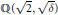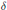Refine search
Actions for selected content:
10 results
On even K-groups over p-adic Lie extensions of global function fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 729-743
- Print publication:
- September 2025
-
- Article
- Export citation
Level compatibility in Sharifi’s conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1194-1212
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic tessellations and generators of
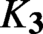 ${K}_{\textbf {3}}$ for imaginary quadratic fields
${K}_{\textbf {3}}$ for imaginary quadratic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 24 May 2021, e40
-
- Article
-
- You have access
- Open access
- Export citation
L-functions for Quadratic Characters and Annihilation of Motivic Cohomology Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 3 / 01 September 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 620-631
- Print publication:
- 01 September 2015
-
- Article
-
- You have access
- Export citation
Iwasawa Theory for K2n
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 02 May 2013, pp. 115-123
- Print publication:
- August 2013
-
- Article
- Export citation
Functoriality of the Canonical Fractional Galois Ideal
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 5 / 01 October 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1011-1036
- Print publication:
- 01 October 2010
-
- Article
-
- You have access
- Export citation
On the 2-Rank of the Hilbert Kernel of Number Fields
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 5 / 01 October 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1073-1091
- Print publication:
- 01 October 2009
-
- Article
-
- You have access
- Export citation
A Note on 4-Rank Densities
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 3 / 01 September 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 431-438
- Print publication:
- 01 September 2004
-
- Article
-
- You have access
- Export citation
Bi-Quadratic Number Fields with Trivial 2-Primary Hilbert Kernels
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 1 / July 2003
- Published online by Cambridge University Press:
- 25 June 2003, pp. 109-136
- Print publication:
- July 2003
-
- Article
- Export citation
A NORM PRINCIPLE IN HIGHER ALGEBRAIC K-THEORY
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 4 / July 2003
- Published online by Cambridge University Press:
- 09 June 2003, pp. 491-498
- Print publication:
- July 2003
-
- Article
- Export citation

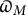
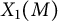
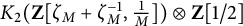
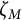
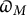
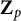
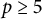
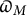
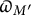
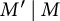
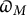
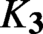
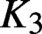
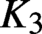
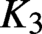
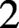
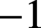
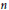
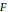
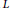
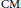

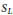
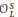
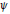
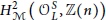
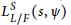
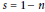
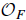
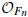 denote its ring of integers. We establish an analogue of the classical Iwasawa theorem for the orders of
denote its ring of integers. We establish an analogue of the classical Iwasawa theorem for the orders of