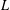 $L$-FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
$L$-FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
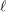 $\ell$-independence
$\ell$-independence
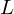 $L$-series of geometrically hyperelliptic curves of genus three
$L$-series of geometrically hyperelliptic curves of genus three
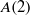 $A(2)$ and
$A(2)$ and 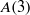 $A(3)$
$A(3)$