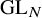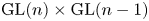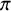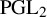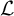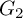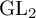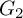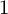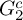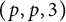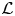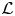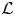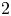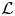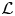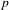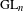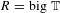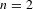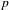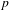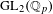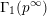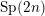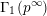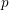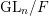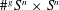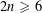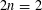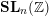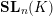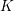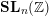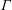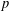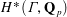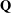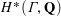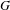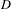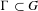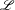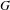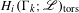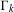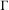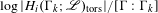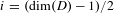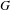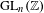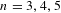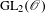Refine search
Actions for selected content:
30 results
VORONOI COMPLEXES IN HIGHER DIMENSIONS, COHOMOLOGY OF
 $GL_N(\mathbb{Z} )$ FOR
$GL_N(\mathbb{Z} )$ FOR  $N\geqslant 8$ AND THE TRIVIALITY OF
$N\geqslant 8$ AND THE TRIVIALITY OF  $K_8(\mathbb{Z} )$
$K_8(\mathbb{Z} )$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-26
-
- Article
- Export citation
Rigid meromorphic cocycles for orthogonal groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 September 2025, e160
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EISENSTEIN COHOMOLOGY FOR ORTHOGONAL GROUPS AND THE SPECIAL VALUES OF L-FUNCTIONS FOR
 $\mathrm {GL}_1 \times \mathrm {O}(2n)$
$\mathrm {GL}_1 \times \mathrm {O}(2n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 2463-2522
- Print publication:
- November 2025
-
- Article
- Export citation
Eisenstein Cohomology for
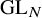 $\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
$\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eisenstein cocycles in motivic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 30 October 2024, pp. 2407-2479
- Print publication:
- October 2024
-
- Article
- Export citation
Period relations for Rankin–Selberg convolutions for
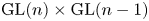 ${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1871-1915
- Print publication:
- August 2024
-
- Article
- Export citation
L-invariants for cohomological representations of PGL(2) over arbitrary number fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING DISCRETE, LEVEL-
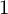 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 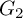 $G_2$
$G_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 2127-2157
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded cohomology is not a profinite invariant
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 379-390
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On ternary Diophantine equations of signature
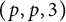 $(p,p,\text{3})$ over number fields
$(p,p,\text{3})$ over number fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1293-1313
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Big principal series,
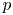 $p$-adic families and
$p$-adic families and 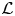 $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 409-436
- Print publication:
- February 2022
-
- Article
- Export citation
AUTOMORPHIC LEFSCHETZ PROPERTIES FOR NONCOMPACT ARITHMETIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1655-1702
- Print publication:
- July 2023
-
- Article
- Export citation
Corrigendum: On the cuspidal cohomology of S-arithmetic subgroups of reductive groups over number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 26 May 2021, pp. 1207-1210
- Print publication:
- June 2021
-
- Article
-
- You have access
- HTML
- Export citation
Profinite invariants of arithmetic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e54
-
- Article
-
- You have access
- Open access
- Export citation
PATCHING AND THE COMPLETED HOMOLOGY OF LOCALLY SYMMETRIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 27 May 2020, pp. 395-458
- Print publication:
- March 2022
-
- Article
- Export citation
Shimura varieties at level
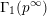 $\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
$\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1152-1230
- Print publication:
- June 2020
-
- Article
- Export citation
ON THE COHOMOLOGY OF TORELLI GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 April 2020, e7
-
- Article
-
- You have access
- Open access
- Export citation
Stability in the high-dimensional cohomology of congruence subgroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 822-861
- Print publication:
- April 2020
-
- Article
- Export citation
DERIVED HECKE ALGEBRA AND COHOMOLOGY OF ARITHMETIC GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 7 / 2019
- Published online by Cambridge University Press:
- 23 December 2019, e7
-
- Article
-
- You have access
- Open access
- Export citation
ON THE GROWTH OF TORSION IN THE COHOMOLOGY OF ARITHMETIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 21 March 2018, pp. 537-569
- Print publication:
- March 2020
-
- Article
- Export citation