Refine search
Actions for selected content:
14 results
RANKS OF SOFT OPERATORS IN NOWHERE SCATTERED
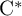 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 371-410
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHEN IS A NUMERICAL SEMIGROUP A QUOTIENT?
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 67-76
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REPRESENTING STRUCTURED SEMIGROUPS ON ÉTALE GROUPOID BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1-49
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The type semigroup, comparison, and almost finiteness for ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 27 October 2021, pp. 361-400
- Print publication:
- February 2023
-
- Article
- Export citation
MOST SIMPLE EXTENSIONS OF
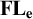 $\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE
$\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1156-1200
- Print publication:
- September 2022
-
- Article
- Export citation
Edwards' condition for quasitraces on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 525-547
- Print publication:
- April 2021
-
- Article
-
- You have access
- Open access
- Export citation
VARIETIES OF DE MORGAN MONOIDS: COVERS OF ATOMS
-
- Journal:
- The Review of Symbolic Logic / Volume 13 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 338-374
- Print publication:
- June 2020
-
- Article
- Export citation
Comparison Properties of the CuntzSemigroup and Applications to C* -algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 1 / 01 February 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 26-52
- Print publication:
- 01 February 2018
-
- Article
-
- You have access
- Export citation
On Radicals of Green’s Relations in Ordered Semigroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 2 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 246-252
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
THE ZELEZNIKOW PROBLEM ON A CLASS OF ADDITIVELY IDEMPOTENT SEMIRINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 05 September 2013, pp. 404-420
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Numerical Semigroups That Are Not Intersections of d-Squashed Semigroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 4 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 598-612
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
TOPOLOGY ON THE SPACES OF ORDERINGS OF GROUPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 4 / July 2004
- Published online by Cambridge University Press:
- 14 June 2004, pp. 519-526
- Print publication:
- July 2004
-
- Article
- Export citation
Ideal Structure of Multiplier Algebras of Simple C *-algebras With Real Rank Zero
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 3 / 01 June 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 592-630
- Print publication:
- 01 June 2001
-
- Article
-
- You have access
- Export citation
The Universal Theory of Ordered Equidecomposability Types Semigroups
-
- Journal:
- Canadian Journal of Mathematics / Volume 46 / Issue 5 / 01 October 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1093-1120
- Print publication:
- 01 October 1994
-
- Article
-
- You have access
- Export citation
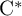
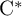
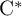
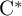
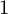
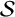
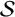
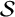
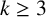
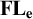
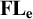
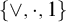
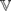
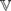

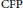

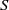


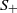
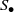
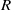
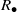
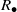
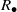
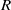
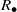
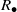
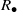
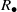
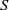

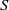
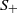

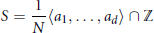
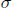
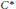
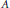
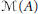
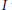
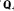
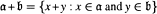 and the ordering defined by
and the ordering defined by 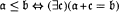 . As a corollary, the set of all universal formulas of (+, ≤) satisfied by all full type spaces is decidable.
. As a corollary, the set of all universal formulas of (+, ≤) satisfied by all full type spaces is decidable.