Published online by Cambridge University Press: 26 January 2019
The variety DMM of De Morgan monoids has just four minimal subvarieties. The join-irreducible covers of these atoms in the subvariety lattice of DMM are investigated. One of the two atoms consisting of idempotent algebras has no such cover; the other has just one. The remaining two atoms lack nontrivial idempotent members. They are generated, respectively, by 4-element De Morgan monoids C4 and D4, where C4 is the only nontrivial 0-generated algebra onto which finitely subdirectly irreducible De Morgan monoids may be mapped by noninjective homomorphisms. The homomorphic preimages of C4 within DMM (together with the trivial De Morgan monoids) constitute a proper quasivariety, which is shown to have a largest subvariety U. The covers of the variety 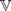 (C4) within U are revealed here. There are just ten of them (all finitely generated). In exactly six of these ten varieties, all nontrivial members have C4 as a retract. In the varietal join of those six classes, every subquasivariety is a variety—in fact, every finite subdirectly irreducible algebra is projective. Beyond U, all covers of
(C4) within U are revealed here. There are just ten of them (all finitely generated). In exactly six of these ten varieties, all nontrivial members have C4 as a retract. In the varietal join of those six classes, every subquasivariety is a variety—in fact, every finite subdirectly irreducible algebra is projective. Beyond U, all covers of 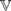 (C4) [or of
(C4) [or of 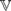 (D4)] within DMM are discriminator varieties. Of these, we identify infinitely many that are finitely generated, and some that are not. We also prove that there are just 68 minimal quasivarieties of De Morgan monoids.
(D4)] within DMM are discriminator varieties. Of these, we identify infinitely many that are finitely generated, and some that are not. We also prove that there are just 68 minimal quasivarieties of De Morgan monoids.