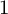1 Introduction
Realizing every strictly positive, lower-semicontinuous, affine function on the tracial state space of a separable, simple, nuclear, nonelementary
![]() $\mathrm {C}^*$
-algebra as the rank of an operator in its stabilization is a deep and open problem, first studied in [Reference Dadarlat and Toms19]. A positive solution to this problem would imply that every separable, simple, nonelementary
$\mathrm {C}^*$
-algebra as the rank of an operator in its stabilization is a deep and open problem, first studied in [Reference Dadarlat and Toms19]. A positive solution to this problem would imply that every separable, simple, nonelementary
![]() $\mathrm {C}^*$
-algebra of locally finite nuclear dimension and strict comparison of positive elements is
$\mathrm {C}^*$
-algebra of locally finite nuclear dimension and strict comparison of positive elements is
![]() $\mathcal {Z}$
-stable, thus proving the remaining implication of the prominent Toms–Winter conjecture ([Reference Winter50, Section 5]) in this case; see, for example, [Reference Thiel37, Section 9] and the discussion in [Reference Castillejos, Evington, Tikuisis and White15, Section 5].
$\mathcal {Z}$
-stable, thus proving the remaining implication of the prominent Toms–Winter conjecture ([Reference Winter50, Section 5]) in this case; see, for example, [Reference Thiel37, Section 9] and the discussion in [Reference Castillejos, Evington, Tikuisis and White15, Section 5].
When the
![]() $\mathrm {C}^*$
-algebra A is not simple, the problem is still of much interest, but one needs to replace the tracial state space by the cone
$\mathrm {C}^*$
-algebra A is not simple, the problem is still of much interest, but one needs to replace the tracial state space by the cone
![]() $ {\mathrm {QT}}(A)$
of lower-semicontinuous, extended-valued
$ {\mathrm {QT}}(A)$
of lower-semicontinuous, extended-valued
![]() $2$
-quasitraces on A. Each such quasitrace extends canonically to the stabilization
$2$
-quasitraces on A. Each such quasitrace extends canonically to the stabilization
![]() $A\otimes {\mathbb {K}}$
, and the rank of an operator
$A\otimes {\mathbb {K}}$
, and the rank of an operator
![]() $a \in (A\otimes {\mathbb {K}})_+$
is defined as the map
$a \in (A\otimes {\mathbb {K}})_+$
is defined as the map
![]() $\widehat {[a]}\colon {\mathrm {QT}}(A)\to [0,\infty ]$
given by
$\widehat {[a]}\colon {\mathrm {QT}}(A)\to [0,\infty ]$
given by
for
![]() $\tau \in {\mathrm {QT}}(A)$
. The rank problem is then to determine which functions on
$\tau \in {\mathrm {QT}}(A)$
. The rank problem is then to determine which functions on
![]() $ {\mathrm {QT}}(A)$
arise as the rank of a positive operator in A or
$ {\mathrm {QT}}(A)$
arise as the rank of a positive operator in A or
![]() $A\otimes {\mathbb {K}}$
.
$A\otimes {\mathbb {K}}$
.
A natural obstruction arises if A has a nonzero elementary ideal quotient, that is, if there are closed ideals
![]() $I \subseteq J \subseteq A$
such that
$I \subseteq J \subseteq A$
such that
![]() $J/I$
is
$J/I$
is
![]() $\ast $
-isomorphic to
$\ast $
-isomorphic to
![]() ${\mathbb {K}}(H)$
for some Hilbert space H. In this case, the natural trace on
${\mathbb {K}}(H)$
for some Hilbert space H. In this case, the natural trace on
![]() ${\mathbb {K}}(H)$
induces a quasitrace
${\mathbb {K}}(H)$
induces a quasitrace
![]() $\tau \in {\mathrm {QT}}(A)$
that is discrete in the sense that
$\tau \in {\mathrm {QT}}(A)$
that is discrete in the sense that
![]() $d_\tau (a) \in \{0,1,2,\ldots ,\infty \}$
for every
$d_\tau (a) \in \{0,1,2,\ldots ,\infty \}$
for every
![]() $a \in (A\otimes {\mathbb {K}})_+$
. A similar obstruction arises in the representation of interpolation groups by continuous, affine functions on their state space; see [Reference Goodearl26, Chapter 8].
$a \in (A\otimes {\mathbb {K}})_+$
. A similar obstruction arises in the representation of interpolation groups by continuous, affine functions on their state space; see [Reference Goodearl26, Chapter 8].
To avoid this obstruction, it is therefore natural to assume that A has no nonzero elementary ideal quotients, a condition termed nowhere scatteredness in [Reference Thiel and Vilalta39]. Building on the results from [Reference Thiel37], the rank problem was solved in [Reference Antoine, Perera, Robert and Thiel2] for nowhere scattered
![]() $\mathrm {C}^*$
-algebras that have stable rank one: Every function on
$\mathrm {C}^*$
-algebras that have stable rank one: Every function on
![]() $ {\mathrm {QT}}(A)$
that satisfies the ‘obvious’ conditions arises as the rank of an operator in
$ {\mathrm {QT}}(A)$
that satisfies the ‘obvious’ conditions arises as the rank of an operator in
![]() $A\otimes {\mathbb {K}}$
; see [Reference Antoine, Perera, Robert and Thiel2, Theorem 7.13] for the precise statement. Moreover, one can arrange for the operator to be soft, which means that it generates a hereditary sub-
$A\otimes {\mathbb {K}}$
; see [Reference Antoine, Perera, Robert and Thiel2, Theorem 7.13] for the precise statement. Moreover, one can arrange for the operator to be soft, which means that it generates a hereditary sub-
![]() $\mathrm {C}^*$
-algebra that has no nonzero unital quotients; see [Reference Thiel and Vilalta40, Definition 3.1].
$\mathrm {C}^*$
-algebra that has no nonzero unital quotients; see [Reference Thiel and Vilalta40, Definition 3.1].
As a consequence, in a nowhere scattered, stable rank one
![]() $\mathrm {C}^*$
-algebra, the rank of every operator can be realized as the rank of a soft operator.
$\mathrm {C}^*$
-algebra, the rank of every operator can be realized as the rank of a soft operator.
The aim of this paper is to study this phenomenon in greater generality and, more concretely, to investigate when the rank of every operator in a
![]() $\mathrm {C}^*$
-algebra A can be realized as the rank of a soft element. We show that this holds whenever A satisfies the Global Glimm Property – a notion conjectured to be equivalent to nowhere scatteredness; see Paragraph 2.3. Namely, we prove:
$\mathrm {C}^*$
-algebra A can be realized as the rank of a soft element. We show that this holds whenever A satisfies the Global Glimm Property – a notion conjectured to be equivalent to nowhere scatteredness; see Paragraph 2.3. Namely, we prove:
Theorem A (5.11).
Let A be a stable
![]() $\mathrm {C}^*$
-algebra with the global Glimm property. Then, for any
$\mathrm {C}^*$
-algebra with the global Glimm property. Then, for any
![]() $a\in A_+$
there exists a soft element
$a\in A_+$
there exists a soft element
![]() $b \in A_+$
with
$b \in A_+$
with
![]() $b \precsim a$
and such that
$b \precsim a$
and such that
for every
![]() $\tau \in {\mathrm {QT}}(A)$
.
$\tau \in {\mathrm {QT}}(A)$
.
In Theorem A above, we use
![]() $\precsim $
to denote the Cuntz subequivalence, a relation between positive elements introduced by Cuntz in [Reference Cuntz18]. This relation allows one to define the Cuntz semigroup, an object that has played an important role in the structure and classification theory of
$\precsim $
to denote the Cuntz subequivalence, a relation between positive elements introduced by Cuntz in [Reference Cuntz18]. This relation allows one to define the Cuntz semigroup, an object that has played an important role in the structure and classification theory of
![]() $\mathrm {C}^*$
-algebras; see Paragraph 2.1 and [Reference Antoine, Perera, Robert and Thiel2, Reference Coward, Elliott and Ivanescu17, Reference Thiel37, Reference Toms45, Reference Winter49]. As explained in Paragraph 2.2, the study of the Cuntz semigroup has often come in hand with the development of abstract Cuntz semigroups, also known as
$\mathrm {C}^*$
-algebras; see Paragraph 2.1 and [Reference Antoine, Perera, Robert and Thiel2, Reference Coward, Elliott and Ivanescu17, Reference Thiel37, Reference Toms45, Reference Winter49]. As explained in Paragraph 2.2, the study of the Cuntz semigroup has often come in hand with the development of abstract Cuntz semigroups, also known as
![]() $\mathrm {Cu}$
-semigroups; see [Reference Antoine, Perera and Thiel5, Reference Antoine, Perera and Thiel6, Reference Antoine, Perera and Thiel7, Reference Cantier and Vilalta14, Reference Robert32, Reference Vilalta47] among many others.
$\mathrm {Cu}$
-semigroups; see [Reference Antoine, Perera and Thiel5, Reference Antoine, Perera and Thiel6, Reference Antoine, Perera and Thiel7, Reference Cantier and Vilalta14, Reference Robert32, Reference Vilalta47] among many others.
If an operator a is soft, then its Cuntz class
![]() $[a]$
is strongly soft (we recall the definition at the beginning of Section 3). If A has the global Glimm property, then every strongly soft Cuntz class arises this way, and it follows that the submonoid
$[a]$
is strongly soft (we recall the definition at the beginning of Section 3). If A has the global Glimm property, then every strongly soft Cuntz class arises this way, and it follows that the submonoid
![]() $ {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
of strongly soft Cuntz classes agrees with the subset of Cuntz classes with a soft representative; see Corollary 3.4.
$ {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
of strongly soft Cuntz classes agrees with the subset of Cuntz classes with a soft representative; see Corollary 3.4.
The cone
![]() $ {\mathrm {QT}}(A)$
is naturally isomorphic to the cone
$ {\mathrm {QT}}(A)$
is naturally isomorphic to the cone
![]() $F( {\mathrm {Cu}}(A))$
of functionals on the Cuntz semigroup
$F( {\mathrm {Cu}}(A))$
of functionals on the Cuntz semigroup
![]() $ {\mathrm {Cu}}(A)$
; see [Reference Elliott, Robert and Santiago20, Theorem 4.4]. As an application of Theorem A, we show that the same is true for the cone of functionals on
$ {\mathrm {Cu}}(A)$
; see [Reference Elliott, Robert and Santiago20, Theorem 4.4]. As an application of Theorem A, we show that the same is true for the cone of functionals on
![]() $ {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
.
$ {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
.
Theorem B (5.15).
Let A be a
![]() $\mathrm {C}^*$
-algebra with the global Glimm property. Then,
$\mathrm {C}^*$
-algebra with the global Glimm property. Then,
![]() $ {\mathrm {QT}}(A)$
is naturally isomorphic to
$ {\mathrm {QT}}(A)$
is naturally isomorphic to
![]() $F( {\mathrm {Cu}} (A)_{\mathrm {{soft}}} )$
.
$F( {\mathrm {Cu}} (A)_{\mathrm {{soft}}} )$
.
We introduce in Section 4 a weak notion of cancellation for Cuntz semigroups, which we term left-soft separativity; see Definition 4.2. Whenever a
![]() $\mathrm {C}^*$
-algebra with the global Glimm property has a left-soft separative Cuntz semigroup, the relation between arbitrary and soft elements from Theorem A can be made more precise:
$\mathrm {C}^*$
-algebra with the global Glimm property has a left-soft separative Cuntz semigroup, the relation between arbitrary and soft elements from Theorem A can be made more precise:
Theorem C (6.3, 6.6).
Let A be a
![]() $\mathrm {C}^*$
-algebra with the global Glimm property. Assume that
$\mathrm {C}^*$
-algebra with the global Glimm property. Assume that
![]() $ {\mathrm {Cu}} (A)$
is left-soft separative. Then;
$ {\mathrm {Cu}} (A)$
is left-soft separative. Then;
-
(i) For every element
 $x\in {\mathrm {Cu}} (A)$
, there exists a greatest element in
$x\in {\mathrm {Cu}} (A)$
, there exists a greatest element in
 $ {\mathrm {Cu}} (A)_{\mathrm {{soft}}}$
below x, denoted by
$ {\mathrm {Cu}} (A)_{\mathrm {{soft}}}$
below x, denoted by
 $\sigma (x)$
.
$\sigma (x)$
. -
(ii) We have
 $\lambda (\sigma (x))=\lambda (x)$
for every
$\lambda (\sigma (x))=\lambda (x)$
for every
 $x \in {\mathrm {Cu}}(A)$
and
$x \in {\mathrm {Cu}}(A)$
and
 $\lambda \in F( {\mathrm {Cu}} (A))$
.
$\lambda \in F( {\mathrm {Cu}} (A))$
. -
(iii) The map
 $\sigma \colon {\mathrm {Cu}} (A)\to {\mathrm {Cu}} (A)_{\mathrm {{soft}}}$
, defined by
$\sigma \colon {\mathrm {Cu}} (A)\to {\mathrm {Cu}} (A)_{\mathrm {{soft}}}$
, defined by
 $x\mapsto \sigma (x)$
, preserves order, suprema of increasing sequences and is superadditive.
$x\mapsto \sigma (x)$
, preserves order, suprema of increasing sequences and is superadditive.
We show in section 4 that the Cuntz semigroup is left-soft separative whenever the
![]() $\mathrm {C}^*$
-algebra has stable rank one or strict comparison of positive elements. Under these assumptions, we also show that
$\mathrm {C}^*$
-algebra has stable rank one or strict comparison of positive elements. Under these assumptions, we also show that
![]() $\sigma $
is subadditive and, consequently, a generalized Cu-morphism; see Theorem 6.9. Then
$\sigma $
is subadditive and, consequently, a generalized Cu-morphism; see Theorem 6.9. Then
![]() $ {\mathrm {Cu}} (A)_{\mathrm {{soft}}}$
is a retract of
$ {\mathrm {Cu}} (A)_{\mathrm {{soft}}}$
is a retract of
![]() $ {\mathrm {Cu}} (A)$
, as defined in [Reference Thiel and Vilalta42].
$ {\mathrm {Cu}} (A)$
, as defined in [Reference Thiel and Vilalta42].
Using structure results of retracts and soft elements, we study the covering dimension ([Reference Thiel and Vilalta42]) and the radius of comparison ([Reference Blackadar, Robert, Tikuisis, Toms and Winter13]) of
![]() $\mathrm {C}^*$
-algebras with the global Glimm property in terms of their soft elements.
$\mathrm {C}^*$
-algebras with the global Glimm property in terms of their soft elements.
Theorem D (7.3).
Let A be a
![]() $\mathrm {C}^*$
-algebra with the global Glimm property. Assume one of the following holds:
$\mathrm {C}^*$
-algebra with the global Glimm property. Assume one of the following holds:
-
(i) A has strict comparison of positive elements;
-
(ii) A has stable rank one;
-
(iii) A has topological dimension zero, and
 $ {\mathrm {Cu}} (A)$
is left-soft separative.
$ {\mathrm {Cu}} (A)$
is left-soft separative.
Then
![]() $\dim ( {\mathrm {Cu}} (A)_{\mathrm {{soft}}})\leq \dim ( {\mathrm {Cu}} (A))\leq \dim ( {\mathrm {Cu}} (A)_{\mathrm {{soft}}})+1$
.
$\dim ( {\mathrm {Cu}} (A)_{\mathrm {{soft}}})\leq \dim ( {\mathrm {Cu}} (A))\leq \dim ( {\mathrm {Cu}} (A)_{\mathrm {{soft}}})+1$
.
Theorem E (8.6).
Let A be a unital, separable
![]() $\mathrm {C}^*$
-algebra with the global Glimm property. Assume that A has stable rank one. Then
$\mathrm {C}^*$
-algebra with the global Glimm property. Assume that A has stable rank one. Then
We finish the paper with some applications of Theorems D and E to crossed products; see Theorem 7.9 and Example 8.9.
2 Preliminaries
In this section, we recall definitions and results that will be used in the sections that follow. The reader is referred to [Reference Ara, Perera and Toms8], [Reference Antoine, Perera and Thiel4] and [Reference Gardella and Perera24] for an extensive introduction to the theory of
![]() $\mathrm {Cu}$
-semigroups and their interplay with Cuntz semigroups.
$\mathrm {Cu}$
-semigroups and their interplay with Cuntz semigroups.
Given a
![]() $\mathrm {C}^*$
-algebra A, we use
$\mathrm {C}^*$
-algebra A, we use
![]() $A_+$
to denote the set of its positive elements.
$A_+$
to denote the set of its positive elements.
2.1 (The Cuntz semigroup).
Let A be a
![]() $\mathrm {C}^*$
-algebra. Given
$\mathrm {C}^*$
-algebra. Given
![]() $a, b \in A_+$
, one says that a is Cuntz subequivalent to b, written
$a, b \in A_+$
, one says that a is Cuntz subequivalent to b, written
![]() $a\precsim b$
if there exists a sequence
$a\precsim b$
if there exists a sequence
![]() $(v_n)_n$
in A such that
$(v_n)_n$
in A such that
![]() $a=\lim _n v_n b v_n^*$
. Further, one says that a is Cuntz equivalent to b, written
$a=\lim _n v_n b v_n^*$
. Further, one says that a is Cuntz equivalent to b, written
![]() $a\sim b$
, if
$a\sim b$
, if
![]() $a\precsim b$
and
$a\precsim b$
and
![]() $b \precsim a$
.
$b \precsim a$
.
The Cuntz semigroup of A, denoted by
![]() $ {\mathrm {Cu}} (A)$
, is the positively ordered monoid defined as the quotient
$ {\mathrm {Cu}} (A)$
, is the positively ordered monoid defined as the quotient
![]() $(A\otimes \mathcal {K})_+/{\sim }$
equipped with the order induced by
$(A\otimes \mathcal {K})_+/{\sim }$
equipped with the order induced by
![]() $\precsim $
and the addition induced by addition of orthogonal elements. For further details, we refer to [Reference Antoine, Perera and Thiel4, Reference Ara, Perera and Toms8, Reference Gardella and Perera24].
$\precsim $
and the addition induced by addition of orthogonal elements. For further details, we refer to [Reference Antoine, Perera and Thiel4, Reference Ara, Perera and Toms8, Reference Gardella and Perera24].
2.2 (
 $\mathrm {Cu}$
-semigroups).
$\mathrm {Cu}$
-semigroups).
Let
![]() $(P, \leq )$
be a partially ordered set. Suppose that every increasing sequence in P has a supremum. Given two elements
$(P, \leq )$
be a partially ordered set. Suppose that every increasing sequence in P has a supremum. Given two elements
![]() $x,y$
in P, one says that x is way below y, denoted
$x,y$
in P, one says that x is way below y, denoted
![]() $x\ll y$
, if for every increasing sequence
$x\ll y$
, if for every increasing sequence
![]() $(z_n)_n$
in P satisfying
$(z_n)_n$
in P satisfying
![]() $y\leq \sup _n z_n$
, there exists some
$y\leq \sup _n z_n$
, there exists some
![]() $m\in {\mathbb {N}}$
such that
$m\in {\mathbb {N}}$
such that
![]() $x\leq z_m$
.
$x\leq z_m$
.
As defined in [Reference Coward, Elliott and Ivanescu17], a
![]() $\mathrm {Cu}$
-semigroup is a positively ordered monoid S satisfying two domain-type conditions and two compatibility conditions:
$\mathrm {Cu}$
-semigroup is a positively ordered monoid S satisfying two domain-type conditions and two compatibility conditions:
-
(O1) Every increasing sequence in S has a supremum.
-
(O2) For every element x in S, there exists a sequence
 $(x_n)_{n}$
in S such that
$(x_n)_{n}$
in S such that
 $x_0 \ll x_1 \ll x_2 \ll \cdots $
and
$x_0 \ll x_1 \ll x_2 \ll \cdots $
and
 $x = \sup _n x_n$
.
$x = \sup _n x_n$
. -
(O3) The addition is compatible with the way-below relation, that is, for every
 $x', x, y', y \in S$
satisfying
$x', x, y', y \in S$
satisfying
 $x' \ll x$
and
$x' \ll x$
and
 $y' \ll y$
, we have
$y' \ll y$
, we have
 $x' + y' \ll x + y$
.
$x' + y' \ll x + y$
. -
(O4) The addition is compatible with suprema of increasing sequences, that is, for every increasing sequences
 $(x_n)_n$
and
$(x_n)_n$
and
 $(y_n)_n$
in S, we have
$(y_n)_n$
in S, we have $$\begin{align*}\sup _n (x_n+y_n) = \sup _nx_n + \sup _ny_n.\end{align*}$$
$$\begin{align*}\sup _n (x_n+y_n) = \sup _nx_n + \sup _ny_n.\end{align*}$$
It follows from [Reference Coward, Elliott and Ivanescu17] that the Cuntz semigroup of any
![]() $\mathrm {C}^*$
-algebra always satisfies (O1)–(O4). Specifically, the Cuntz semigroup of any
$\mathrm {C}^*$
-algebra always satisfies (O1)–(O4). Specifically, the Cuntz semigroup of any
![]() $\mathrm {C}^*$
-algebra is a
$\mathrm {C}^*$
-algebra is a
![]() $\mathrm {Cu}$
-semigroup.
$\mathrm {Cu}$
-semigroup.
Given a monoid morphism
![]() $\varphi $
between two
$\varphi $
between two
![]() $\mathrm {Cu}$
-semigroups, we say that
$\mathrm {Cu}$
-semigroups, we say that
![]() $\varphi $
is a
$\varphi $
is a
![]() $\mathrm {Cu}$
-morphism if it preserves the order, suprema of increasing sequences and the way-below relation. A generalized
$\mathrm {Cu}$
-morphism if it preserves the order, suprema of increasing sequences and the way-below relation. A generalized
![]() $\mathrm {Cu}$
-morphism is a monoid map that preserves order and suprema of increasing sequences (but not necessarily the way-below relation).
$\mathrm {Cu}$
-morphism is a monoid map that preserves order and suprema of increasing sequences (but not necessarily the way-below relation).
The following properties, which will often be considered throughout the paper, are also satisfied in the Cuntz semigroup of any
![]() $\mathrm {C}^*$
-algebra; see [Reference Antoine, Perera and Thiel4, Proposition 4.6] and its precursor [Reference Rørdam and Winter35, Lemma 7.1] for (O5), [Reference Robert32, Proposition 5.1.1] for (O6) and [Reference Antoine, Perera, Robert and Thiel1, Proposition 2.2] for (O7).
$\mathrm {C}^*$
-algebra; see [Reference Antoine, Perera and Thiel4, Proposition 4.6] and its precursor [Reference Rørdam and Winter35, Lemma 7.1] for (O5), [Reference Robert32, Proposition 5.1.1] for (O6) and [Reference Antoine, Perera, Robert and Thiel1, Proposition 2.2] for (O7).
-
(O5) For every
 $x, y, x', y', z\in S$
satisfying
$x, y, x', y', z\in S$
satisfying
 $x+y\leq z$
and
$x+y\leq z$
and
 $x'\ll x$
and
$x'\ll x$
and
 $y'\ll y$
, there exists
$y'\ll y$
, there exists
 $c \in S$
such that
$c \in S$
such that
 $y'\ll c$
and
$y'\ll c$
and
 $x'+c\leq z \leq x+c$
.
$x'+c\leq z \leq x+c$
.This property is often applied with
 $y'=y=0$
.
$y'=y=0$
. -
(O6) For every
 $x, x', y, z\in S$
satisfying
$x, x', y, z\in S$
satisfying
 $x'\ll x\ll y+z$
, there exist
$x'\ll x\ll y+z$
, there exist
 $v, w \in S$
such that
$v, w \in S$
such that  $$\begin{align*}v \leq x,y, \quad w \leq x,z, \,\,\,\text{ and }\,\,\, x'\leq v+w. \end{align*}$$
$$\begin{align*}v \leq x,y, \quad w \leq x,z, \,\,\,\text{ and }\,\,\, x'\leq v+w. \end{align*}$$
-
(O7) For every
 $x, x', y, y', w \in S$
satisfying
$x, x', y, y', w \in S$
satisfying
 $x'\ll x\leq w$
and
$x'\ll x\leq w$
and
 $y'\ll y\leq w$
, there exists
$y'\ll y\leq w$
, there exists
 $z \in S$
such that
$z \in S$
such that
 $x',y'\ll z\leq w,x+y$
.
$x',y'\ll z\leq w,x+y$
.
Given an element x in a
![]() $\mathrm {Cu}$
-semigroup, we denote by
$\mathrm {Cu}$
-semigroup, we denote by
![]() $\infty x$
the supremum of the increasing sequence
$\infty x$
the supremum of the increasing sequence
![]() $(nx)_n$
.
$(nx)_n$
.
2.3 (The Global Glimm Property and nowhere scatteredness).
A
![]() $\mathrm {C}^*$
-algebra A is said to be nowhere scattered if no hereditary sub-
$\mathrm {C}^*$
-algebra A is said to be nowhere scattered if no hereditary sub-
![]() $\mathrm {C}^*$
-algebra of A has a nonzero one-dimensional representation. Equivalently, A is nowhere scattered if and only if A has no nonzero elementary ideal quotients; see [Reference Thiel and Vilalta39, Definition A] and [Reference Thiel and Vilalta39, Theorem 3.1].
$\mathrm {C}^*$
-algebra of A has a nonzero one-dimensional representation. Equivalently, A is nowhere scattered if and only if A has no nonzero elementary ideal quotients; see [Reference Thiel and Vilalta39, Definition A] and [Reference Thiel and Vilalta39, Theorem 3.1].
We say that A has the global Glimm property (in the sense of [Reference Kirchberg and Rørdam29, Definition 4.12]) if, for every
![]() $a\in A_+$
and
$a\in A_+$
and
![]() $\varepsilon>0$
, there exists a square-zero element
$\varepsilon>0$
, there exists a square-zero element
![]() $r\in \overline {aAa}$
such that
$r\in \overline {aAa}$
such that
![]() $(a-\varepsilon )_+\in \overline {\mathrm {span}}ArA$
; see [Reference Thiel and Vilalta43, Section 3].
$(a-\varepsilon )_+\in \overline {\mathrm {span}}ArA$
; see [Reference Thiel and Vilalta43, Section 3].
A
![]() $\mathrm {C}^*$
-algebra satisfying the global Glimm property is always nowhere scattered. The converse remains open and is known as the global Glimm problem. The problem has been answered affirmatively under the additional assumption of real rank zero ([Reference Elliott and Rørdam21]) or stable rank one ([Reference Antoine, Perera, Robert and Thiel2]).
$\mathrm {C}^*$
-algebra satisfying the global Glimm property is always nowhere scattered. The converse remains open and is known as the global Glimm problem. The problem has been answered affirmatively under the additional assumption of real rank zero ([Reference Elliott and Rørdam21]) or stable rank one ([Reference Antoine, Perera, Robert and Thiel2]).
A
![]() $\mathrm {Cu}$
-semigroup is said to be
$\mathrm {Cu}$
-semigroup is said to be
![]() $(2,\omega )$
-divisible if, for every pair
$(2,\omega )$
-divisible if, for every pair
![]() $x',x\in S$
with
$x',x\in S$
with
![]() $x'\ll x$
, there exists
$x'\ll x$
, there exists
![]() $y\in S$
such that
$y\in S$
such that
![]() $2y\leq x$
and
$2y\leq x$
and
![]() $x'\leq \infty y$
; see [Reference Robert and Rørdam33, Definition 5.1].
$x'\leq \infty y$
; see [Reference Robert and Rørdam33, Definition 5.1].
For a detailed study of the global Glimm problem and its relation with the Cuntz semigroup, we refer to [Reference Thiel and Vilalta43]; see also [Reference Vilalta48]. Among other results, it follows from [Reference Thiel and Vilalta43, Theorem 3.6] that a
![]() $\mathrm {C}^*$
-algebra A has the global Glimm property if and only if
$\mathrm {C}^*$
-algebra A has the global Glimm property if and only if
![]() $ {\mathrm {Cu}} (A)$
is
$ {\mathrm {Cu}} (A)$
is
![]() $(2,\omega )$
-divisible.
$(2,\omega )$
-divisible.
3 Soft operators and strongly soft Cuntz classes
In this section, we first recall the definitions of (completely) soft operators in
![]() $\mathrm {C}^*$
-algebras and of strongly soft elements in
$\mathrm {C}^*$
-algebras and of strongly soft elements in
![]() $\mathrm {Cu}$
-semigroups. We then connect these notions and show that, for a
$\mathrm {Cu}$
-semigroups. We then connect these notions and show that, for a
![]() $\mathrm {C}^*$
-algebra A with the global Glimm property, an element in the Cuntz semigroup
$\mathrm {C}^*$
-algebra A with the global Glimm property, an element in the Cuntz semigroup
![]() $ {\mathrm {Cu}}(A)$
is strongly soft if and only if it has a soft representative; see Theorem 3.3 and Corollary 3.4.
$ {\mathrm {Cu}}(A)$
is strongly soft if and only if it has a soft representative; see Theorem 3.3 and Corollary 3.4.
As defined in [Reference Thiel and Vilalta40, Definition 4.2], an element x in a
![]() $\mathrm {Cu}$
-semigroup S is strongly soft if for all
$\mathrm {Cu}$
-semigroup S is strongly soft if for all
![]() $x' \in S$
with
$x' \in S$
with
![]() $x' \ll x$
there exists
$x' \ll x$
there exists
![]() $t\in S$
such that
$t\in S$
such that
This notion of softness is stronger than the one considered in [Reference Antoine, Perera and Thiel4, Definition 5.3.1]. However, if S is residually stably finite, both notions agree; see [Reference Thiel and Vilalta40, Proposition 4.6]. In particular, this applies to weakly cancellative
![]() $\mathrm {Cu}$
-semigroups (see Paragraph 4.1 below).
$\mathrm {Cu}$
-semigroups (see Paragraph 4.1 below).
As mentioned in the introduction, a positive element a in a
![]() $\mathrm {C}^*$
-algebra A is said to be soft if its hereditary sub-
$\mathrm {C}^*$
-algebra A is said to be soft if its hereditary sub-
![]() $\mathrm {C}^*$
-algebra has no nonzero unital quotients. This definition can be seen as a generalization of pure positivity, a notion introduced in [Reference Perera and Toms30, Definition 2.1] for simple
$\mathrm {C}^*$
-algebra has no nonzero unital quotients. This definition can be seen as a generalization of pure positivity, a notion introduced in [Reference Perera and Toms30, Definition 2.1] for simple
![]() $\mathrm {C}^*$
-algebras. An element
$\mathrm {C}^*$
-algebras. An element
![]() $a \in A_+$
is said to be completely soft if
$a \in A_+$
is said to be completely soft if
![]() $(a-\varepsilon )_+$
is soft for every
$(a-\varepsilon )_+$
is soft for every
![]() $\varepsilon>0$
, where
$\varepsilon>0$
, where
![]() $(a-\varepsilon )_+$
denotes the ‘cut down’ of a given by applying functional calculus to a with the function
$(a-\varepsilon )_+$
denotes the ‘cut down’ of a given by applying functional calculus to a with the function
![]() $f(t)=\max \{t-\varepsilon ,0\}$
.
$f(t)=\max \{t-\varepsilon ,0\}$
.
As in [Reference Thiel and Vilalta40, Definition 5.2], we say that a
![]() $\mathrm {C}^*$
-algebra A has an abundance of soft elements if, for every
$\mathrm {C}^*$
-algebra A has an abundance of soft elements if, for every
![]() $a\in A_+$
and
$a\in A_+$
and
![]() $\varepsilon>0$
, there exists a positive, soft element
$\varepsilon>0$
, there exists a positive, soft element
![]() $b \in \overline {aAa}$
such that
$b \in \overline {aAa}$
such that
![]() $(a-\varepsilon )_+\in \overline {\mathrm {span}}AbA$
. By [Reference Thiel and Vilalta40, Proposition 7.7], any
$(a-\varepsilon )_+\in \overline {\mathrm {span}}AbA$
. By [Reference Thiel and Vilalta40, Proposition 7.7], any
![]() $\mathrm {C}^*$
-algebra with the global Glimm property has an abundance of soft elements.
$\mathrm {C}^*$
-algebra with the global Glimm property has an abundance of soft elements.
If
![]() $a \in A_+$
is soft, then its Cuntz class
$a \in A_+$
is soft, then its Cuntz class
![]() $[a]$
is strongly soft; see [Reference Thiel and Vilalta40, Proposition 4.16]. Conversely, we prove in Theorem 3.3 below that if A has an abundance of soft elements (in particular, if A has the global Glimm property), then every strongly soft Cuntz class arises this way, that is, a Cuntz class
$[a]$
is strongly soft; see [Reference Thiel and Vilalta40, Proposition 4.16]. Conversely, we prove in Theorem 3.3 below that if A has an abundance of soft elements (in particular, if A has the global Glimm property), then every strongly soft Cuntz class arises this way, that is, a Cuntz class
![]() $[b] \in {\mathrm {Cu}}(A)$
is strongly soft if and only if there exists a soft element
$[b] \in {\mathrm {Cu}}(A)$
is strongly soft if and only if there exists a soft element
![]() $a \in (A\otimes {\mathbb {K}})_+$
with
$a \in (A\otimes {\mathbb {K}})_+$
with
![]() $b\sim a$
. It remains unclear if this also holds for general
$b\sim a$
. It remains unclear if this also holds for general
![]() $\mathrm {C}^*$
-algebras; see [Reference Thiel and Vilalta40, Question 4.17].
$\mathrm {C}^*$
-algebras; see [Reference Thiel and Vilalta40, Question 4.17].
Given
![]() $a,b\in A_+$
, we will write
$a,b\in A_+$
, we will write
![]() $a\vartriangleleft b$
whenever
$a\vartriangleleft b$
whenever
![]() $a\in \overline {\mathrm {span}}AbA$
. We say that two positive elements a and b in a
$a\in \overline {\mathrm {span}}AbA$
. We say that two positive elements a and b in a
![]() $\mathrm {C}^*$
-algebra are orthognal if
$\mathrm {C}^*$
-algebra are orthognal if
![]() $ab=0$
.
$ab=0$
.
The next result is the
![]() $\mathrm {C}^*$
-algebraic analog of [Reference Thiel and Vilalta40, Theorem 4.14(2)].
$\mathrm {C}^*$
-algebraic analog of [Reference Thiel and Vilalta40, Theorem 4.14(2)].
Proposition 3.1. Let a and b be orthogonal positive elements in a
![]() $\mathrm {C}^*$
-algebra such that
$\mathrm {C}^*$
-algebra such that
![]() $a \lhd b$
and such that b is soft. Then
$a \lhd b$
and such that b is soft. Then
![]() $a+b$
is soft.
$a+b$
is soft.
Proof. By [Reference Thiel and Vilalta40, Proposition 3.6], a positive element c in a
![]() $\mathrm {C}^*$
-algebra is soft if and only if for every
$\mathrm {C}^*$
-algebra is soft if and only if for every
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $r \in (\overline {cAc})_+$
such that r is orthogonal to
$r \in (\overline {cAc})_+$
such that r is orthogonal to
![]() $(c-\varepsilon )_+$
and such that
$(c-\varepsilon )_+$
and such that
![]() $c \lhd r$
. Using this characterization for b, we show that it is satisfied for
$c \lhd r$
. Using this characterization for b, we show that it is satisfied for
![]() $a+b$
.
$a+b$
.
To verify that
![]() $a+b$
is soft, let
$a+b$
is soft, let
![]() $\varepsilon>0$
. Using that b is soft, we obtain
$\varepsilon>0$
. Using that b is soft, we obtain
![]() $r \in (\overline {bAb})_+$
such that r is orthogonal to
$r \in (\overline {bAb})_+$
such that r is orthogonal to
![]() $(b-\varepsilon )_+$
and such that
$(b-\varepsilon )_+$
and such that
![]() $b \lhd r$
. Since a and b are orthogonal, we have
$b \lhd r$
. Since a and b are orthogonal, we have
Since r belongs to
![]() $\overline {bAb}$
, it is also orthogonal to a, and thus also orthogonal to
$\overline {bAb}$
, it is also orthogonal to a, and thus also orthogonal to
![]() $((a+b)-\varepsilon )_+$
. Further, we have
$((a+b)-\varepsilon )_+$
. Further, we have
![]() $a+b \lhd b \lhd r$
, as desired.
$a+b \lhd b \lhd r$
, as desired.
Lemma 3.2. Let A be a
![]() $\mathrm {C}^*$
-algebra with an abundance of soft elements, let
$\mathrm {C}^*$
-algebra with an abundance of soft elements, let
![]() $a \in A_+$
be such that
$a \in A_+$
be such that
![]() $x:=[a]\in {\mathrm {Cu}} (A)$
is strongly soft, and let
$x:=[a]\in {\mathrm {Cu}} (A)$
is strongly soft, and let
![]() $x' \in {\mathrm {Cu}}(A)$
satisfy
$x' \in {\mathrm {Cu}}(A)$
satisfy
![]() $x'\ll x$
. Then there exists a positive, completely soft element
$x'\ll x$
. Then there exists a positive, completely soft element
![]() $b \in \overline {aAa}$
such that
$b \in \overline {aAa}$
such that
Proof. Choose
![]() $x"\in {\mathrm {Cu}} (A)$
such that
$x"\in {\mathrm {Cu}} (A)$
such that
![]() $x'\ll x"\ll x$
. Using that x is strongly soft, we know that there exists
$x'\ll x"\ll x$
. Using that x is strongly soft, we know that there exists
![]() $t\in {\mathrm {Cu}} (A)$
such that
$t\in {\mathrm {Cu}} (A)$
such that
![]() $x"\ll \infty t$
and
$x"\ll \infty t$
and
![]() $x"+t\ll x$
. Choose orthogonal positive elements
$x"+t\ll x$
. Choose orthogonal positive elements
![]() $c,d \in A\otimes {\mathbb {K}}$
and
$c,d \in A\otimes {\mathbb {K}}$
and
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
Using that
![]() $c+d \precsim a$
, we can apply Rørdam’s lemma (see, for example, [Reference Thiel36, Theorem 2.30]) to obtain
$c+d \precsim a$
, we can apply Rørdam’s lemma (see, for example, [Reference Thiel36, Theorem 2.30]) to obtain
![]() $x \in A\otimes {\mathbb {K}}$
such that
$x \in A\otimes {\mathbb {K}}$
such that
Set
Then
![]() $c',d' \in \overline {aAa}$
. Since c and d are orthogonal, we have
$c',d' \in \overline {aAa}$
. Since c and d are orthogonal, we have
It follows that
![]() $c'$
and
$c'$
and
![]() $d'$
are orthogonal and that
$d'$
are orthogonal and that
![]() $c' \sim (c-\varepsilon )_+$
and
$c' \sim (c-\varepsilon )_+$
and
![]() $d' \sim (d-\varepsilon )_+$
.
$d' \sim (d-\varepsilon )_+$
.
In particular, we have
![]() $x" \ll \infty [(d-\varepsilon )_+] = \infty [d']$
, and we obtain
$x" \ll \infty [(d-\varepsilon )_+] = \infty [d']$
, and we obtain
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $x" \ll \infty [(d'-\delta )_+]$
. Applying that A has an abundance of soft elements for
$x" \ll \infty [(d'-\delta )_+]$
. Applying that A has an abundance of soft elements for
![]() $d'$
and
$d'$
and
![]() $\delta $
, we obtain a soft element
$\delta $
, we obtain a soft element
![]() $e \in (\overline {d'Ad'})_+$
such that
$e \in (\overline {d'Ad'})_+$
such that
![]() $(d'-\delta )_+ \lhd e$
. Since
$(d'-\delta )_+ \lhd e$
. Since
![]() $c'$
and
$c'$
and
![]() $d'$
are orthogonal, and e belongs to
$d'$
are orthogonal, and e belongs to
![]() $\overline {d'Ad'}$
, it follows that
$\overline {d'Ad'}$
, it follows that
![]() $c'$
and e are orthogonal.
$c'$
and e are orthogonal.
Using that positive elements
![]() $g,h$
in a
$g,h$
in a
![]() $\mathrm {C}^*$
-algebra satisfy
$\mathrm {C}^*$
-algebra satisfy
![]() $g \lhd h$
if and only if
$g \lhd h$
if and only if
![]() $[g] \leq \infty [h]$
, we have
$[g] \leq \infty [h]$
, we have
and thus
![]() $c' \lhd e$
. By Proposition 3.1,
$c' \lhd e$
. By Proposition 3.1,
![]() $c'+e$
is soft.
$c'+e$
is soft.
Note that
![]() $c'$
and e belong to
$c'$
and e belong to
![]() $\overline {aAa}$
. In particular,
$\overline {aAa}$
. In particular,
![]() $c'+e$
belongs to
$c'+e$
belongs to
![]() $A_+$
, and we can apply [Reference Thiel and Vilalta40, Theorem 6.9] to obtain a completely soft element
$A_+$
, and we can apply [Reference Thiel and Vilalta40, Theorem 6.9] to obtain a completely soft element
![]() $f \in A_+$
such that
$f \in A_+$
such that
![]() $\overline {fAf} = \overline {(c'+e)A(c'+e)} \subseteq \overline {aAa}$
. Then
$\overline {fAf} = \overline {(c'+e)A(c'+e)} \subseteq \overline {aAa}$
. Then
![]() $f \in \overline {aAa}$
, and therefore
$f \in \overline {aAa}$
, and therefore
![]() $[f] \leq [a] = x$
. Further, we have
$[f] \leq [a] = x$
. Further, we have
Choose
![]() $\delta>0$
such that
$\delta>0$
such that
and set
![]() $b := (f-\delta )_+$
. Since cut downs of
$b := (f-\delta )_+$
. Since cut downs of
![]() $(f-\delta )_+$
are also cut downs of f, we see that b is completely soft. Further, we have
$(f-\delta )_+$
are also cut downs of f, we see that b is completely soft. Further, we have
which shows that b has the desired properties.
A unital
![]() $\mathrm {C}^*$
-algebra is said to have stable rank one if its invertible elements are norm dense, and a general
$\mathrm {C}^*$
-algebra is said to have stable rank one if its invertible elements are norm dense, and a general
![]() $\mathrm {C}^*$
-algebra is said to have stable rank one if its minimal unitization does; see [Reference Blackadar12, Section V.3.1].
$\mathrm {C}^*$
-algebra is said to have stable rank one if its minimal unitization does; see [Reference Blackadar12, Section V.3.1].
A
![]() $\mathrm {C}^*$
-algebra is said to have weak stable rank one if
$\mathrm {C}^*$
-algebra is said to have weak stable rank one if
![]() $A\subseteq \overline {\mathrm {Gl}(\tilde {A})}$
. Any stable
$A\subseteq \overline {\mathrm {Gl}(\tilde {A})}$
. Any stable
![]() $\mathrm {C}^*$
-algebra has weak stable rank one; see [Reference Blackadar, Robert, Tikuisis, Toms and Winter13, Lemma 4.3.2].
$\mathrm {C}^*$
-algebra has weak stable rank one; see [Reference Blackadar, Robert, Tikuisis, Toms and Winter13, Lemma 4.3.2].
Theorem 3.3. Let A be a
![]() $\mathrm {C}^*$
-algebra with an abundance of soft elements, and let
$\mathrm {C}^*$
-algebra with an abundance of soft elements, and let
![]() $a\in A_+$
be such that
$a\in A_+$
be such that
![]() $[a]\in {\mathrm {Cu}} (A)$
is strongly soft. Then there exists a sequence
$[a]\in {\mathrm {Cu}} (A)$
is strongly soft. Then there exists a sequence
![]() $(a_n)_n$
of completely soft elements in
$(a_n)_n$
of completely soft elements in
![]() $(\overline {aAa})_+$
such that
$(\overline {aAa})_+$
such that
![]() $([a_n])_n$
in
$([a_n])_n$
in
![]() $ {\mathrm {Cu}}(A)$
is
$ {\mathrm {Cu}}(A)$
is
![]() $\ll $
-increasing with
$\ll $
-increasing with
![]() $[a] = \sup _n [a_n]$
.
$[a] = \sup _n [a_n]$
.
If, moreover, A has weak stable rank one, then
![]() $[a]$
is strongly soft if and only if there exists a completely soft element
$[a]$
is strongly soft if and only if there exists a completely soft element
![]() $b\in A_+$
such that
$b\in A_+$
such that
![]() $[a]=[b]$
.
$[a]=[b]$
.
Proof. Choose a
![]() $\ll $
-increasing sequence
$\ll $
-increasing sequence
![]() $(x_n)_n$
in
$(x_n)_n$
in
![]() $ {\mathrm {Cu}} (A)$
with supremum
$ {\mathrm {Cu}} (A)$
with supremum
![]() $[a]$
. We will inductively choose completely soft elements
$[a]$
. We will inductively choose completely soft elements
![]() $a_n \in (\overline {aAa})_+$
such that
$a_n \in (\overline {aAa})_+$
such that
for
![]() $n\in {\mathbb {N}}$
. To start, apply Lemma 3.2 for
$n\in {\mathbb {N}}$
. To start, apply Lemma 3.2 for
![]() $x_0 \ll [a]$
to obtain a completely soft element
$x_0 \ll [a]$
to obtain a completely soft element
![]() $a_0 \in (\overline {aAa})_+$
such that
$a_0 \in (\overline {aAa})_+$
such that
![]() $x_0 \ll [a_0] \ll [a]$
. Assuming we have chosen
$x_0 \ll [a_0] \ll [a]$
. Assuming we have chosen
![]() $a_0,\ldots ,a_n$
, find
$a_0,\ldots ,a_n$
, find
![]() $x_n' \in {\mathrm {Cu}}(A)$
such that
$x_n' \in {\mathrm {Cu}}(A)$
such that
![]() $[a_n],x_n \ll x_n' \ll [a]$
. Applying Lemma 3.2 for
$[a_n],x_n \ll x_n' \ll [a]$
. Applying Lemma 3.2 for
![]() $x_n' \ll [a]$
, we obtain a completely soft element
$x_n' \ll [a]$
, we obtain a completely soft element
![]() $a_{n+1} \in (\overline {aAa})_+$
such that
$a_{n+1} \in (\overline {aAa})_+$
such that
![]() $x_n' \ll [a_{n+1}] \ll [a]$
. Proceeding inductively, we obtain the desired sequence
$x_n' \ll [a_{n+1}] \ll [a]$
. Proceeding inductively, we obtain the desired sequence
![]() $(a_n)_n$
.
$(a_n)_n$
.
Next, assume that A has weak stable rank one. By [Reference Thiel and Vilalta40, Proposition 4.16], soft operators have strongly soft Cuntz classes. Conversely, assuming that
![]() $[a]$
is strongly soft, we will show that
$[a]$
is strongly soft, we will show that
![]() $[a] = [b]$
for some completely soft element
$[a] = [b]$
for some completely soft element
![]() $b\in A_+$
.
$b\in A_+$
.
Let
![]() $(a_n)_n$
be as above. We will show that
$(a_n)_n$
be as above. We will show that
![]() $\sup _n [a_n]$
(which is
$\sup _n [a_n]$
(which is
![]() $[a]$
), has a soft representative. Given
$[a]$
), has a soft representative. Given
![]() $c,d \in A_+$
, we will write
$c,d \in A_+$
, we will write
![]() $c \sim _u d$
if there exists a unitary
$c \sim _u d$
if there exists a unitary
![]() $u\in \tilde {A}$
such that
$u\in \tilde {A}$
such that
![]() $c=udu^*$
, and we write
$c=udu^*$
, and we write
![]() $c \subseteq d$
if
$c \subseteq d$
if
![]() $\overline {cAc} \subseteq \overline {dAd}$
.
$\overline {cAc} \subseteq \overline {dAd}$
.
Using [Reference Thiel36, §2.5], one can find a sequence
![]() $(\delta _n)_n$
in
$(\delta _n)_n$
in
![]() $(0,\infty )$
and a sequence of contractive elements
$(0,\infty )$
and a sequence of contractive elements
![]() $(b_n)_n$
in
$(b_n)_n$
in
![]() $A_+$
such that
$A_+$
such that
 $$\begin{align*}\begin{matrix} a_1 & \precsim & a_2 & \precsim & a_3 & \precsim & \ldots\\{\leq} & & {\leq} & &{\leq} & &\\(a_1-\delta_1)_+ & & (a_2-\delta_2)_+ & & (a_3-\delta_3)_+ & & \ldots \\{\sim_u} & & {\sim_u} & & {\sim_u} & &\\b_1 & \subseteq & b_2 & \subseteq & b_3 & \subseteq & \ldots \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} a_1 & \precsim & a_2 & \precsim & a_3 & \precsim & \ldots\\{\leq} & & {\leq} & &{\leq} & &\\(a_1-\delta_1)_+ & & (a_2-\delta_2)_+ & & (a_3-\delta_3)_+ & & \ldots \\{\sim_u} & & {\sim_u} & & {\sim_u} & &\\b_1 & \subseteq & b_2 & \subseteq & b_3 & \subseteq & \ldots \end{matrix} \end{align*}$$
and, setting
![]() $b_\infty :=\sum _n \frac {1}{2^n \Vert b_n \Vert } b_n$
, such that
$b_\infty :=\sum _n \frac {1}{2^n \Vert b_n \Vert } b_n$
, such that
![]() $[b_\infty ]=\sup _n [a_n]$
.
$[b_\infty ]=\sup _n [a_n]$
.
For each
![]() $n\in {\mathbb {N}}$
, since
$n\in {\mathbb {N}}$
, since
![]() $a_n$
is completely soft, so is the element
$a_n$
is completely soft, so is the element
![]() $(a_n-\delta _n )_+$
. Since
$(a_n-\delta _n )_+$
. Since
![]() $(a_n-\delta _n )_+$
and
$(a_n-\delta _n )_+$
and
![]() $b_n$
are unitarily equivalent, they generate
$b_n$
are unitarily equivalent, they generate
![]() $\ast $
-isomorphic hereditary sub-
$\ast $
-isomorphic hereditary sub-
![]() $\mathrm {C}^*$
-algebras of A, and it follows that
$\mathrm {C}^*$
-algebras of A, and it follows that
![]() $b_n$
is completely soft as well.
$b_n$
is completely soft as well.
Further, since
![]() $b_0\subseteq b_1\subseteq \ldots $
and
$b_0\subseteq b_1\subseteq \ldots $
and
![]() $b_\infty =\sum _n \frac {1}{2^n \Vert b_n \Vert } b_n$
, the sequence of hereditary sub-
$b_\infty =\sum _n \frac {1}{2^n \Vert b_n \Vert } b_n$
, the sequence of hereditary sub-
![]() $\mathrm {C}^*$
-algebras
$\mathrm {C}^*$
-algebras
![]() $\overline {b_{n}Ab_{n}}$
is increasing with
$\overline {b_{n}Ab_{n}}$
is increasing with
![]() $\overline {b_\infty A b_\infty } = \overline {\bigcup _n \overline {b_n A b_n}}$
. Since each
$\overline {b_\infty A b_\infty } = \overline {\bigcup _n \overline {b_n A b_n}}$
. Since each
![]() $\overline {b_n A b_n}$
has no nonzero unital quotients, it follows from [Reference Thiel and Vilalta40, Proposition 2.17] that neither does
$\overline {b_n A b_n}$
has no nonzero unital quotients, it follows from [Reference Thiel and Vilalta40, Proposition 2.17] that neither does
![]() $\overline {b_\infty A b_\infty }$
. This proves that
$\overline {b_\infty A b_\infty }$
. This proves that
![]() $b_\infty $
is soft.
$b_\infty $
is soft.
Note that
![]() $b_\infty $
belongs to
$b_\infty $
belongs to
![]() $A_+$
. Applying [Reference Thiel and Vilalta40, Theorem 6.9], we obtain a completely soft element
$A_+$
. Applying [Reference Thiel and Vilalta40, Theorem 6.9], we obtain a completely soft element
![]() $b \in A_+$
such that
$b \in A_+$
such that
![]() $\overline {bAb} = \overline {b_\infty A b_\infty }$
. Then
$\overline {bAb} = \overline {b_\infty A b_\infty }$
. Then
![]() $[b]=[b_\infty ]=[a]$
, as desired.
$[b]=[b_\infty ]=[a]$
, as desired.
Corollary 3.4. Let A be a
![]() $\mathrm {C}^*$
-algebra with the global Glimm property, and let
$\mathrm {C}^*$
-algebra with the global Glimm property, and let
![]() $x \in {\mathrm {Cu}}(A)$
. Then x is strongly soft if and only if there exists a soft element
$x \in {\mathrm {Cu}}(A)$
. Then x is strongly soft if and only if there exists a soft element
![]() $a \in (A\otimes {\mathbb {K}})_+$
with
$a \in (A\otimes {\mathbb {K}})_+$
with
![]() $x = [a]$
.
$x = [a]$
.
Proof. It follows from [Reference Thiel and Vilalta43, Theorem 3.6] that
![]() $A\otimes {\mathbb {K}}$
has the global Glimm property. Hence,
$A\otimes {\mathbb {K}}$
has the global Glimm property. Hence,
![]() $A\otimes {\mathbb {K}}$
has an abundance of soft elements by [Reference Thiel and Vilalta43, Proposition 7.7]. Further,
$A\otimes {\mathbb {K}}$
has an abundance of soft elements by [Reference Thiel and Vilalta43, Proposition 7.7]. Further,
![]() $A\otimes {\mathbb {K}}$
has weak stable rank one by [Reference Blackadar, Robert, Tikuisis, Toms and Winter13, Lemma 4.3.2]. Now, the result follows from Theorem 3.3.
$A\otimes {\mathbb {K}}$
has weak stable rank one by [Reference Blackadar, Robert, Tikuisis, Toms and Winter13, Lemma 4.3.2]. Now, the result follows from Theorem 3.3.
3.5 (The strongly soft subsemigroup).
Given a
![]() $\mathrm {Cu}$
-semigroup S, we let
$\mathrm {Cu}$
-semigroup S, we let
![]() $S_{\mathrm {{soft}}}$
denote the set of strongly soft elements in S. By Corollary 3.4, given a
$S_{\mathrm {{soft}}}$
denote the set of strongly soft elements in S. By Corollary 3.4, given a
![]() $\mathrm {C}^*$
-algebra A with the global Glimm property, we have
$\mathrm {C}^*$
-algebra A with the global Glimm property, we have
In particular, if A is stably finite, simple and unital, it follows from [Reference Thiel and Vilalta40, Proposition 4.16] that the subset
![]() $ {\mathrm {Cu}} (A)_{\mathrm {{soft}}}\setminus \{ 0\}$
coincides with
$ {\mathrm {Cu}} (A)_{\mathrm {{soft}}}\setminus \{ 0\}$
coincides with
![]() $ {\mathrm {Cu}}_{+} (A)$
, the set of Cuntz classes of purely positive elements as introduced in [Reference Perera and Toms30, Definition 2.1]; see also [Reference Asadi-Vasfi, Golestani and Phillips11, Definition 3.8].
$ {\mathrm {Cu}}_{+} (A)$
, the set of Cuntz classes of purely positive elements as introduced in [Reference Perera and Toms30, Definition 2.1]; see also [Reference Asadi-Vasfi, Golestani and Phillips11, Definition 3.8].
Given a
![]() $\mathrm {Cu}$
-semigroup S, a sub-
$\mathrm {Cu}$
-semigroup S, a sub-
![]() $\mathrm {Cu}$
-semigroup in the sense of [Reference Thiel and Vilalta38, Definition 4.1] is a submonoid
$\mathrm {Cu}$
-semigroup in the sense of [Reference Thiel and Vilalta38, Definition 4.1] is a submonoid
![]() $T \subseteq S$
that is a
$T \subseteq S$
that is a
![]() $\mathrm {Cu}$
-semigroup for the inherited order and such that the inclusion map
$\mathrm {Cu}$
-semigroup for the inherited order and such that the inclusion map
![]() $T \to S$
is a
$T \to S$
is a
![]() $\mathrm {Cu}$
-morphism.
$\mathrm {Cu}$
-morphism.
Proposition 3.6. Let S be a
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup that satisfies (O5). Then,
$\mathrm {Cu}$
-semigroup that satisfies (O5). Then,
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup that also satisfies (O5).
$\mathrm {Cu}$
-semigroup that also satisfies (O5).
If S also satisfies (O6) (respectively (O7)), then so does
![]() $S_{\mathrm {{soft}}}$
.
$S_{\mathrm {{soft}}}$
.
Proof. By [Reference Thiel and Vilalta40, Proposition 7.7], if a
![]() $\mathrm {Cu}$
-semigroup is
$\mathrm {Cu}$
-semigroup is
![]() $(2,\omega )$
-divisible and satisfies (O5), then it has an abundance of soft elements, which then by [Reference Thiel and Vilalta40, Proposition 5.6] implies that its strongly soft elements form a sub-
$(2,\omega )$
-divisible and satisfies (O5), then it has an abundance of soft elements, which then by [Reference Thiel and Vilalta40, Proposition 5.6] implies that its strongly soft elements form a sub-
![]() $\mathrm {Cu}$
-semigroup. Thus,
$\mathrm {Cu}$
-semigroup. Thus,
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup.
$\mathrm {Cu}$
-semigroup.
Let us verify that
![]() $S_{\mathrm {{soft}}}$
satisfies (O5). By [Reference Antoine, Perera and Thiel4, Theorem 4.4(1)] it suffices to show that for all
$S_{\mathrm {{soft}}}$
satisfies (O5). By [Reference Antoine, Perera and Thiel4, Theorem 4.4(1)] it suffices to show that for all
![]() $x',x,y',y,z',z \in S_{\mathrm {{soft}}}$
satisfying
$x',x,y',y,z',z \in S_{\mathrm {{soft}}}$
satisfying
there exist
![]() $c',c \in S_{\mathrm {{soft}}}$
such that
$c',c \in S_{\mathrm {{soft}}}$
such that
So let
![]() $x',x,y',y,z',z \in S_{\mathrm {{soft}}}$
satisfy Equation (1). Choose
$x',x,y',y,z',z \in S_{\mathrm {{soft}}}$
satisfy Equation (1). Choose
![]() $v',v \in S_{\mathrm {{soft}}}$
such that
$v',v \in S_{\mathrm {{soft}}}$
such that
Applying (O5), we obtain
![]() $b \in S$
such that
$b \in S$
such that
Using that
![]() $v' \ll v$
and that v is strongly soft, we apply [Reference Thiel and Vilalta40, Proposition 4.13] to find
$v' \ll v$
and that v is strongly soft, we apply [Reference Thiel and Vilalta40, Proposition 4.13] to find
![]() $t \in S_{\mathrm {{soft}}}$
such that
$t \in S_{\mathrm {{soft}}}$
such that
![]() $v'+t \leq v \leq \infty t$
. Set
$v'+t \leq v \leq \infty t$
. Set
![]() $c := b+t$
. Since
$c := b+t$
. Since
![]() $b \leq v' \leq v \leq \infty t$
and t is strongly soft, we have
$b \leq v' \leq v \leq \infty t$
and t is strongly soft, we have
![]() $c \in S_{\mathrm {{soft}}}$
by [Reference Thiel and Vilalta40, Theorem 4.14(2)]. Thus, one gets
$c \in S_{\mathrm {{soft}}}$
by [Reference Thiel and Vilalta40, Theorem 4.14(2)]. Thus, one gets
and
Using also that
![]() $S_{\mathrm {{soft}}}$
is a
$S_{\mathrm {{soft}}}$
is a
![]() $\mathrm {Cu}$
-semigroup and
$\mathrm {Cu}$
-semigroup and
![]() $c \in S_{\mathrm {{soft}}}$
, we can find
$c \in S_{\mathrm {{soft}}}$
, we can find
![]() $c' \in S_{\mathrm {{soft}}}$
such that
$c' \in S_{\mathrm {{soft}}}$
such that
This shows that
![]() $c'$
and c satisfy Equation (2), as desired.
$c'$
and c satisfy Equation (2), as desired.
That
![]() $S_{\mathrm {{soft}}}$
satisfies (O6) (respectively (O7)) whenever S does is proven analogously.
$S_{\mathrm {{soft}}}$
satisfies (O6) (respectively (O7)) whenever S does is proven analogously.
4 Separative
 $\mathrm {Cu}$
-semigroups
$\mathrm {Cu}$
-semigroups
We introduce in Definition 4.2 the notion of left-soft separativity, a weakening of weak cancellation (Paragraph 4.1) that is satisfied in the Cuntz semigroup of every
![]() $\mathrm {C}^*$
-algebra with stable rank one or strict comparison of positive elements; see Proposition 4.3 and Proposition 4.8, respectively. We also prove in Proposition 4.6 that, among strongly soft elements, the notions of unperforation and almost unperforation coincide.
$\mathrm {C}^*$
-algebra with stable rank one or strict comparison of positive elements; see Proposition 4.3 and Proposition 4.8, respectively. We also prove in Proposition 4.6 that, among strongly soft elements, the notions of unperforation and almost unperforation coincide.
4.1 (Cuntz semigroups of stable rank one
 $\mathrm {C}^*$
-algebras).
$\mathrm {C}^*$
-algebras).
Let A be a stable rank one
![]() $\mathrm {C}^*$
-algebra. As shown in [Reference Rørdam and Winter35, Theorem 4.3], the Cuntz semigroup
$\mathrm {C}^*$
-algebra. As shown in [Reference Rørdam and Winter35, Theorem 4.3], the Cuntz semigroup
![]() $ {\mathrm {Cu}} (A)$
satisfies a cancellation property termed weak cancellation: If
$ {\mathrm {Cu}} (A)$
satisfies a cancellation property termed weak cancellation: If
![]() $x,y,z \in {\mathrm {Cu}}(A)$
satisfy
$x,y,z \in {\mathrm {Cu}}(A)$
satisfy
![]() $x+z\ll y+z$
, then
$x+z\ll y+z$
, then
![]() $x\ll y$
.
$x\ll y$
.
If A is also separable, then
![]() $ {\mathrm {Cu}}(A)$
is inf-semilattice ordered, that is, for every pair of elements
$ {\mathrm {Cu}}(A)$
is inf-semilattice ordered, that is, for every pair of elements
![]() $x,y \in {\mathrm {Cu}}(A)$
their infimum
$x,y \in {\mathrm {Cu}}(A)$
their infimum
![]() $x \wedge y$
exists, and for every
$x \wedge y$
exists, and for every
![]() $x,y,z \in {\mathrm {Cu}}(A)$
one has
$x,y,z \in {\mathrm {Cu}}(A)$
one has
![]() $(x+z) \wedge (y+z) = (x \wedge y) +z$
; see [Reference Antoine, Perera, Robert and Thiel2, Theorem 3.8].
$(x+z) \wedge (y+z) = (x \wedge y) +z$
; see [Reference Antoine, Perera, Robert and Thiel2, Theorem 3.8].
As defined in [Reference Thiel and Vilalta41], a
![]() $\mathrm {Cu}$
-semigroup is separative if
$\mathrm {Cu}$
-semigroup is separative if
![]() $x \ll y$
whenever
$x \ll y$
whenever
![]() $x+t\ll y+t$
with
$x+t\ll y+t$
with
![]() $t\ll \infty x,\infty y$
. This and other cancellation properties will be studied in more detail in [Reference Thiel and Vilalta41].
$t\ll \infty x,\infty y$
. This and other cancellation properties will be studied in more detail in [Reference Thiel and Vilalta41].
For the results in this paper, we will need the following tailored definition:
Definition 4.2. We say that a
![]() $\mathrm {Cu}$
-semigroup S is left-soft separative if, for any triple of elements
$\mathrm {Cu}$
-semigroup S is left-soft separative if, for any triple of elements
![]() $y,t\in S$
and
$y,t\in S$
and
![]() $x\in S_{\mathrm {{soft}}}$
satisfying
$x\in S_{\mathrm {{soft}}}$
satisfying
we have
![]() $x\ll y$
.
$x\ll y$
.
Proposition 4.3. Every weakly cancellative
![]() $\mathrm {Cu}$
-semigroup is separative, and every separative
$\mathrm {Cu}$
-semigroup is separative, and every separative
![]() $\mathrm {Cu}$
-semigroup is left-soft separative.
$\mathrm {Cu}$
-semigroup is left-soft separative.
In particular, the Cuntz semigroup of every stable rank one
![]() $\mathrm {C}^*$
-algebra is left-soft separative.
$\mathrm {C}^*$
-algebra is left-soft separative.
Proof. It follows directly from the definitions that weak cancellation is stronger than left-soft separativitiy. By [Reference Rørdam and Winter35, Theorem 4.3], the Cuntz semigroup of a stable rank one
![]() $\mathrm {C}^*$
-algebra is weakly cancellative.
$\mathrm {C}^*$
-algebra is weakly cancellative.
Lemma 4.4. Let S be a
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5). Then, S is left-soft separative if and only if for all
$\mathrm {Cu}$
-semigroup satisfying (O5). Then, S is left-soft separative if and only if for all
![]() $y,t',t\in S$
and
$y,t',t\in S$
and
![]() $x\in S_{\mathrm {{soft}}}$
satisfying
$x\in S_{\mathrm {{soft}}}$
satisfying
we have
![]() $x \leq y$
.
$x \leq y$
.
Proof. The backwards implication is straightforward to verify and even holds for general
![]() $\mathrm {Cu}$
-semigroups. To show the forward implication, assume that S is left-soft separative, and let
$\mathrm {Cu}$
-semigroups. To show the forward implication, assume that S is left-soft separative, and let
![]() $x,y,t',t\in S$
as in the statement. By Proposition 3.6, we know that
$x,y,t',t\in S$
as in the statement. By Proposition 3.6, we know that
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup. In particular, x can be written as the supremum of a
$\mathrm {Cu}$
-semigroup. In particular, x can be written as the supremum of a
![]() $\ll $
-increasing sequence of strongly soft elements.
$\ll $
-increasing sequence of strongly soft elements.
Take
![]() $x'\in S_{\mathrm {{soft}}}$
such that
$x'\in S_{\mathrm {{soft}}}$
such that
![]() $x'\ll x$
. We have
$x'\ll x$
. We have
By left-soft separativity, we deduce
![]() $x'\ll y$
. Since x is the supremum of such
$x'\ll y$
. Since x is the supremum of such
![]() $x'$
, one gets
$x'$
, one gets
![]() $x\leq y$
, as required.
$x\leq y$
, as required.
Lemma 4.5. Let S be a left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5), and let
$\mathrm {Cu}$
-semigroup satisfying (O5), and let
![]() $x,t \in S_{\mathrm {{soft}}}$
and
$x,t \in S_{\mathrm {{soft}}}$
and
![]() $y,t' \in S$
satisfy
$y,t' \in S$
satisfy
Then
![]() $x \leq y$
.
$x \leq y$
.
Proof. Take
![]() $t"\in S$
such that
$t"\in S$
such that
![]() $t'\ll t"\ll t$
. Using that t is strongly soft, one finds
$t'\ll t"\ll t$
. Using that t is strongly soft, one finds
![]() $s\in S_{\mathrm {{soft}}}$
such that
$s\in S_{\mathrm {{soft}}}$
such that
![]() $t"+s\leq t\leq \infty s$
; see [Reference Thiel and Vilalta40, Proposition 4.13]. Note that, since x and s are strongly soft, so is
$t"+s\leq t\leq \infty s$
; see [Reference Thiel and Vilalta40, Proposition 4.13]. Note that, since x and s are strongly soft, so is
![]() $x+s$
by [Reference Thiel and Vilalta40, Theorem 4.14]. We get
$x+s$
by [Reference Thiel and Vilalta40, Theorem 4.14]. We get
Further, we have
![]() $t'\ll \infty y$
and
$t'\ll \infty y$
and
![]() $t'\ll t"\leq \infty s\leq \infty (x+s)$
.
$t'\ll t"\leq \infty s\leq \infty (x+s)$
.
An application of Lemma 4.4 shows that
![]() $x+s\leq y$
and, therefore, that
$x+s\leq y$
and, therefore, that
![]() $x\leq y$
.
$x\leq y$
.
The following result shows that three different versions of unperforation coincide for the semigroup of strongly soft elements in a
![]() $\mathrm {Cu}$
-semigroup. Given elements x and y in a partially ordered monoid, one writes
$\mathrm {Cu}$
-semigroup. Given elements x and y in a partially ordered monoid, one writes
![]() $x<_sy$
if there exists
$x<_sy$
if there exists
![]() $n \geq 1$
such that
$n \geq 1$
such that
![]() $(n+1)x \leq ny$
, and one writes
$(n+1)x \leq ny$
, and one writes
![]() $x \leq _p y$
if there exists
$x \leq _p y$
if there exists
![]() $n_0 \in {\mathbb {N}}$
such that
$n_0 \in {\mathbb {N}}$
such that
![]() $nx \leq ny$
for all
$nx \leq ny$
for all
![]() $n \geq n_0$
. We refer to [Reference Antoine, Perera and Thiel4, Chapter 5] for details regarding these definitions.
$n \geq n_0$
. We refer to [Reference Antoine, Perera and Thiel4, Chapter 5] for details regarding these definitions.
Proposition 4.6. Let S be a
![]() $\mathrm {Cu}$
-semigroup. The following are equivalent:
$\mathrm {Cu}$
-semigroup. The following are equivalent:
-
(1)
 $S_{\mathrm {{soft}}}$
is unperforated: If
$S_{\mathrm {{soft}}}$
is unperforated: If
 $x,y \in S_{\mathrm {{soft}}}$
and
$x,y \in S_{\mathrm {{soft}}}$
and
 $n \geq 1$
satisfy
$n \geq 1$
satisfy
 $nx \leq ny$
, then
$nx \leq ny$
, then
 $x \leq y$
.
$x \leq y$
. -
(2)
 $S_{\mathrm {{soft}}}$
is nearly unperforated: If
$S_{\mathrm {{soft}}}$
is nearly unperforated: If
 $x,y \in S_{\mathrm {{soft}}}$
satisfy
$x,y \in S_{\mathrm {{soft}}}$
satisfy
 $x \leq _p y$
, then
$x \leq _p y$
, then
 $x \leq y$
.
$x \leq y$
. -
(3)
 $S_{\mathrm {{soft}}}$
is almost unperforated: If
$S_{\mathrm {{soft}}}$
is almost unperforated: If
 $x,y \in S_{\mathrm {{soft}}}$
satisfy
$x,y \in S_{\mathrm {{soft}}}$
satisfy
 $x <_s y$
, then
$x <_s y$
, then
 $x \leq y$
.
$x \leq y$
.
Proof. In general, (1) implies (2), which implies (3); see [Reference Antoine, Perera and Thiel4, Proposition 5.6.3]. To verify that (3) implies (1), let
![]() $x,y\in S_{\mathrm {{soft}}}$
and
$x,y\in S_{\mathrm {{soft}}}$
and
![]() $n\geq 1$
satisfy
$n\geq 1$
satisfy
![]() $nx\leq ny$
. Then
$nx\leq ny$
. Then
![]() $\widehat {x} \leq \widehat {y}$
; see Paragraph 5.1. By [Reference Thiel and Vilalta40, Proposition 4.5], x is functionally soft. Thus, we deduce from [Reference Antoine, Perera and Thiel4, Theorem 5.3.12] that
$\widehat {x} \leq \widehat {y}$
; see Paragraph 5.1. By [Reference Thiel and Vilalta40, Proposition 4.5], x is functionally soft. Thus, we deduce from [Reference Antoine, Perera and Thiel4, Theorem 5.3.12] that
![]() $x \leq y$
, as desired.
$x \leq y$
, as desired.
Lemma 4.7. Every almost unperforated
![]() $\mathrm {Cu}$
-semigroup satisfying (O5) is left-soft separative.
$\mathrm {Cu}$
-semigroup satisfying (O5) is left-soft separative.
Proof. Let S be an almost unperforated
![]() $\mathrm {Cu}$
-semigroup satisfying (O5). To verify that S is left-soft separative, let
$\mathrm {Cu}$
-semigroup satisfying (O5). To verify that S is left-soft separative, let
![]() $y,t\in S$
and
$y,t\in S$
and
![]() $x\in S_{\mathrm {{soft}}}$
satisfy
$x\in S_{\mathrm {{soft}}}$
satisfy
![]() $x+t\ll y+t$
and
$x+t\ll y+t$
and
![]() $t\ll \infty x,\infty y$
. Choose
$t\ll \infty x,\infty y$
. Choose
![]() $y'\in S$
such that
$y'\in S$
such that
Then
![]() $x \leq _p y'$
by [Reference Antoine, Perera and Thiel4, Proposition 5.6.8(ii)]. In particular, there exists
$x \leq _p y'$
by [Reference Antoine, Perera and Thiel4, Proposition 5.6.8(ii)]. In particular, there exists
![]() $k\in {\mathbb {N}}$
such that
$k\in {\mathbb {N}}$
such that
![]() $kx\leq ky'$
, and thus
$kx\leq ky'$
, and thus
![]() $\widehat {x} \leq \widehat {y'}$
; see Paragraph 5.1. By [Reference Thiel and Vilalta40, Proposition 4.5], x is functionally soft. Using that S is almost unperforated, we obtain that
$\widehat {x} \leq \widehat {y'}$
; see Paragraph 5.1. By [Reference Thiel and Vilalta40, Proposition 4.5], x is functionally soft. Using that S is almost unperforated, we obtain that
![]() $x \leq y' \ll y$
, by [Reference Antoine, Perera and Thiel4, Theorem 5.3.12].
$x \leq y' \ll y$
, by [Reference Antoine, Perera and Thiel4, Theorem 5.3.12].
A
![]() $\mathrm {C}^*$
-algebra A is said to have strict comparison of positive elements if, for all
$\mathrm {C}^*$
-algebra A is said to have strict comparison of positive elements if, for all
![]() $a,b \in (A\otimes {\mathbb {K}})_+$
and some
$a,b \in (A\otimes {\mathbb {K}})_+$
and some
![]() $\varepsilon>0$
, one has that
$\varepsilon>0$
, one has that
![]() $d_\tau (a) \leq (1-\varepsilon )d_\tau (b)$
for all
$d_\tau (a) \leq (1-\varepsilon )d_\tau (b)$
for all
![]() $\tau \in {\mathrm {QT}}(A)$
implies
$\tau \in {\mathrm {QT}}(A)$
implies
![]() $a \precsim b$
.
$a \precsim b$
.
Proposition 4.8. Let A be a
![]() $\mathrm {C}^*$
-algebra with strict comparison of positive elements. Then
$\mathrm {C}^*$
-algebra with strict comparison of positive elements. Then
![]() $ {\mathrm {Cu}} (A)$
is left-soft separative.
$ {\mathrm {Cu}} (A)$
is left-soft separative.
Proof. A
![]() $\mathrm {C}^*$
-algebra has strict comparison of positive elements if and only if its Cuntz semigroup is almost unperforated; see [Reference Elliott, Robert and Santiago20, Proposition 6.2]. Since every Cuntz semigroup satisfies (O5), the result follows from Lemma 4.7.
$\mathrm {C}^*$
-algebra has strict comparison of positive elements if and only if its Cuntz semigroup is almost unperforated; see [Reference Elliott, Robert and Santiago20, Proposition 6.2]. Since every Cuntz semigroup satisfies (O5), the result follows from Lemma 4.7.
Since every
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $\mathrm {C}^*$
-algebra has strict comparison of positive elements (see [Reference Rørdam34, Theorem 4.5]), one gets the following:
$\mathrm {C}^*$
-algebra has strict comparison of positive elements (see [Reference Rørdam34, Theorem 4.5]), one gets the following:
Corollary 4.9. The Cuntz semigroup of every
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $\mathrm {C}^*$
-algebra is left-soft separative.
$\mathrm {C}^*$
-algebra is left-soft separative.
5 Ranks and soft elements
Given a
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup S satisfying (O5)–(O7) (for example, the Cuntz semigroup of a
$\mathrm {Cu}$
-semigroup S satisfying (O5)–(O7) (for example, the Cuntz semigroup of a
![]() $\mathrm {C}^*$
-algebra with the global Glimm property) and an element
$\mathrm {C}^*$
-algebra with the global Glimm property) and an element
![]() $x\in S$
, we show in Theorem 5.10 that there exists a strongly soft element w below x which agrees with x at the level of functionals, that is, the rank of x coincides with the rank of w; see Paragraph 5.1. Paired with Theorem 3.3, this implies that the rank of any positive element in a
$x\in S$
, we show in Theorem 5.10 that there exists a strongly soft element w below x which agrees with x at the level of functionals, that is, the rank of x coincides with the rank of w; see Paragraph 5.1. Paired with Theorem 3.3, this implies that the rank of any positive element in a
![]() $\mathrm {C}^*$
-algebra satisfying the global Glimm property is the rank of a soft element (Theorem 5.11).
$\mathrm {C}^*$
-algebra satisfying the global Glimm property is the rank of a soft element (Theorem 5.11).
Using Theorem 5.10, we also prove that
![]() $F(S)$
, the set of functionals on S, is homeomorphic to
$F(S)$
, the set of functionals on S, is homeomorphic to
![]() $F(S_{\mathrm {{soft}}} )$
; see Theorem 5.14.
$F(S_{\mathrm {{soft}}} )$
; see Theorem 5.14.
5.1 (Functionals and ranks).
Given a
![]() $\mathrm {Cu}$
-semigroup S, we will denote by
$\mathrm {Cu}$
-semigroup S, we will denote by
![]() $F(S)$
the set of its functionals, that is to say, the set of monoid morphisms
$F(S)$
the set of its functionals, that is to say, the set of monoid morphisms
![]() $S\to [0,\infty ]$
that preserve the order and suprema of increasing sequences. If S satisfies (O5), then
$S\to [0,\infty ]$
that preserve the order and suprema of increasing sequences. If S satisfies (O5), then
![]() $F(S)$
becomes a compact, Hausdorff space – and even an algebraically ordered compact cone [Reference Antoine, Perera, Robert and Thiel1, Section 3] – when equipped with a natural topology [Reference Elliott, Robert and Santiago20, Reference Keimel28, Reference Robert32].
$F(S)$
becomes a compact, Hausdorff space – and even an algebraically ordered compact cone [Reference Antoine, Perera, Robert and Thiel1, Section 3] – when equipped with a natural topology [Reference Elliott, Robert and Santiago20, Reference Keimel28, Reference Robert32].
Given a
![]() $\mathrm {C}^*$
-algebra, the cone
$\mathrm {C}^*$
-algebra, the cone
![]() $ {\mathrm {QT}}(A)$
of lower-semicontinuous 2-quasitraces on A is naturally isomorphic to
$ {\mathrm {QT}}(A)$
of lower-semicontinuous 2-quasitraces on A is naturally isomorphic to
![]() $F( {\mathrm {Cu}}(A))$
, as shown in [Reference Elliott, Robert and Santiago20, Theorem 4.4].
$F( {\mathrm {Cu}}(A))$
, as shown in [Reference Elliott, Robert and Santiago20, Theorem 4.4].
We let
![]() $ {\mathrm {LAff}}(F(S))$
denote the monoid of lower-semicontinuous, affine functions
$ {\mathrm {LAff}}(F(S))$
denote the monoid of lower-semicontinuous, affine functions
![]() $F(S)\to (-\infty ,\infty ]$
, equipped with pointwise order and addition. For
$F(S)\to (-\infty ,\infty ]$
, equipped with pointwise order and addition. For
![]() $x\in S$
, the rank of x is defined as the map
$x\in S$
, the rank of x is defined as the map
![]() $\widehat {x} \colon F(S) \to [0,\infty ]$
given by
$\widehat {x} \colon F(S) \to [0,\infty ]$
given by
for
![]() $\lambda \in F(S)$
. The function
$\lambda \in F(S)$
. The function
![]() $\widehat {x}$
belongs to
$\widehat {x}$
belongs to
![]() $ {\mathrm {LAff}}(F(S))$
and the rank problem of determining which functions in
$ {\mathrm {LAff}}(F(S))$
and the rank problem of determining which functions in
![]() $ {\mathrm {LAff}}(F(S))$
arise this way has been studied extensively in [Reference Thiel37] and [Reference Antoine, Perera, Robert and Thiel2].
$ {\mathrm {LAff}}(F(S))$
arise this way has been studied extensively in [Reference Thiel37] and [Reference Antoine, Perera, Robert and Thiel2].
Sending an element
![]() $x \in S$
to its rank
$x \in S$
to its rank
![]() $\widehat {x}$
defines a monoid morphism from S to
$\widehat {x}$
defines a monoid morphism from S to
![]() $ {\mathrm {LAff}} (F(S))$
which preserves both the order and suprema of increasing sequences.
$ {\mathrm {LAff}} (F(S))$
which preserves both the order and suprema of increasing sequences.
Lemma 5.2. Let S be a
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5), and let
$\mathrm {Cu}$
-semigroup satisfying (O5), and let
![]() $u\in S_{\mathrm {{soft}}}$
and
$u\in S_{\mathrm {{soft}}}$
and
![]() $u',x\in S$
be such that
$u',x\in S$
be such that
Then, there exists
![]() $c\in S_{\mathrm {{soft}}} $
satisfying
$c\in S_{\mathrm {{soft}}} $
satisfying
Proof. Let
![]() $u"\in S$
be such that
$u"\in S$
be such that
![]() $u'\ll u"\ll u$
. By [Reference Thiel and Vilalta40, Proposition 4.13], there exists
$u'\ll u"\ll u$
. By [Reference Thiel and Vilalta40, Proposition 4.13], there exists
![]() $s\in S$
satisfying
$s\in S$
satisfying
Since
![]() $u"\ll u\leq \infty s$
, there exists
$u"\ll u\leq \infty s$
, there exists
![]() $s' \in S$
such that
$s' \in S$
such that
We have
Applying (O5), we obtain
![]() $d\in S$
such that
$d\in S$
such that
![]() $u'+d\leq x\leq u"+d$
with
$u'+d\leq x\leq u"+d$
with
![]() $s'\leq d$
. Since
$s'\leq d$
. Since
![]() $u"\leq \infty s'$
, it follows that
$u"\leq \infty s'$
, it follows that
![]() $x\leq \infty d$
. Finally, apply [Reference Thiel and Vilalta40, Proposition 7.7] to d in order to obtain
$x\leq \infty d$
. Finally, apply [Reference Thiel and Vilalta40, Proposition 7.7] to d in order to obtain
![]() $c\in S_{\mathrm {{soft}}}$
such that
$c\in S_{\mathrm {{soft}}}$
such that
![]() $2c\leq d\leq \infty c$
. This element satisfies the required conditions.
$2c\leq d\leq \infty c$
. This element satisfies the required conditions.
A
![]() $\mathrm {Cu}$
-semigroup S is said to be countably based if it contains a countable subset
$\mathrm {Cu}$
-semigroup S is said to be countably based if it contains a countable subset
![]() $D\subseteq S$
such that every element in S can be written as the supremum of an increasing sequence of elements in D. Separable
$D\subseteq S$
such that every element in S can be written as the supremum of an increasing sequence of elements in D. Separable
![]() $\mathrm {C}^*$
-algebras have countably based Cuntz semigroups; see, for example, [Reference Antoine, Perera and Santiago3].
$\mathrm {C}^*$
-algebras have countably based Cuntz semigroups; see, for example, [Reference Antoine, Perera and Santiago3].
Lemma 5.3. Let S be a countably based,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
![]() $x\in S$
. Consider the set
$x\in S$
. Consider the set
Then, for every
![]() $k \in {\mathbb {N}}$
,
$k \in {\mathbb {N}}$
,
![]() $x'\in S$
such that
$x'\in S$
such that
![]() $x'\ll x$
, and
$x'\ll x$
, and
![]() $u',v'\in L_x$
, there exists a strongly soft element
$u',v'\in L_x$
, there exists a strongly soft element
![]() $w'\in L_x$
such that
$w'\in L_x$
such that
If, additionally, S is left-soft separative,
![]() $w'$
may be chosen such that
$w'$
may be chosen such that
![]() $v' \ll w'$
.
$v' \ll w'$
.
Proof. Let
![]() $u',v'\in L_x$
, let
$u',v'\in L_x$
, let
![]() $x' \in S$
satisfy
$x' \in S$
satisfy
![]() $x' \ll x$
, and let
$x' \ll x$
, and let
![]() $k \in {\mathbb {N}}$
. By definition, there exist
$k \in {\mathbb {N}}$
. By definition, there exist
![]() $u,v\in S_{\mathrm {{soft}}}$
such that
$u,v\in S_{\mathrm {{soft}}}$
such that
Choose
![]() $y',y\in S$
such that
$y',y\in S$
such that
Using that
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup by Proposition 3.6, we can choose elements
$\mathrm {Cu}$
-semigroup by Proposition 3.6, we can choose elements
![]() $u",u"',v" \in S_{\mathrm {{soft}}}$
such that
$u",u"',v" \in S_{\mathrm {{soft}}}$
such that
Applying Lemma 5.2 for
![]() $u"'\ll u\ll y$
and
$u"'\ll u\ll y$
and
![]() $v"\ll v\ll y$
, we obtain
$v"\ll v\ll y$
, we obtain
![]() $c,d \in S_{\mathrm {{soft}}}$
such that
$c,d \in S_{\mathrm {{soft}}}$
such that
Then, applying [Reference Thiel and Vilalta43, Proposition 4.10] for
![]() $y'\ll y\leq \infty c,\infty d$
, we get
$y'\ll y\leq \infty c,\infty d$
, we get
![]() $e\in S$
such that
$e\in S$
such that
By [Reference Thiel and Vilalta40, Proposition 7.7], there exists a strongly soft element
![]() $e_0$
such that
$e_0$
such that
![]() $e_0 \leq e \leq \infty e_0$
. Replacing e by
$e_0 \leq e \leq \infty e_0$
. Replacing e by
![]() $e_0$
, we may assume that
$e_0$
, we may assume that
![]() $e \in S_{\mathrm {{soft}}}$
. Using again that
$e \in S_{\mathrm {{soft}}}$
. Using again that
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup, we can find
$\mathrm {Cu}$
-semigroup, we can find
![]() $e',e"\in S_{\mathrm {{soft}}}$
satisfying
$e',e"\in S_{\mathrm {{soft}}}$
satisfying
By [Reference Thiel and Vilalta40, Proposition 4.13], there exists
![]() $r\in S$
such that
$r\in S$
such that
Since
![]() $e"\ll e$
, we can find
$e"\ll e$
, we can find
![]() $r' \in S$
such that
$r' \in S$
such that
Thus, one has
Applying (O5), we obtain
![]() $z\in S$
such that
$z\in S$
such that
Using again that
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup, choose
$\mathrm {Cu}$
-semigroup, choose
![]() $d' \in S_{\mathrm {{soft}}}$
such that
$d' \in S_{\mathrm {{soft}}}$
such that
We have
with
![]() $v"+d\in S_{\mathrm {{soft}}}$
. Note that
$v"+d\in S_{\mathrm {{soft}}}$
. Note that
In particular, since
![]() $d'\ll \infty z$
, there exists
$d'\ll \infty z$
, there exists
![]() $M\in {\mathbb {N}}$
such that
$M\in {\mathbb {N}}$
such that
![]() $d'\leq Mz$
. Set
$d'\leq Mz$
. Set
where
![]() $z\wedge l$
exists because l is idempotent, and S is countably based and satisfies (O7); see [Reference Antoine, Perera, Robert and Thiel1, Theorem 2.4].
$z\wedge l$
exists because l is idempotent, and S is countably based and satisfies (O7); see [Reference Antoine, Perera, Robert and Thiel1, Theorem 2.4].
Note that, since
![]() $l\leq \infty y'\leq \infty e'$
and
$l\leq \infty y'\leq \infty e'$
and
![]() $e'\in S_{\mathrm {{soft}}}$
, it follows from [Reference Thiel and Vilalta40, Theorem 4.14] that
$e'\in S_{\mathrm {{soft}}}$
, it follows from [Reference Thiel and Vilalta40, Theorem 4.14] that
![]() $w\in S_{\mathrm {{soft}}}$
. We get
$w\in S_{\mathrm {{soft}}}$
. We get
By [Reference Antoine, Perera, Robert and Thiel1, Theorem 2.5], the map
![]() $S \to S$
,
$S \to S$
,
![]() $s \mapsto s\wedge l$
, is additive. Using this at the second and fourth step, we get
$s \mapsto s\wedge l$
, is additive. Using this at the second and fourth step, we get
 $$ \begin{align*} v" + 2(d'\wedge l) &= (v" \wedge l) + 2(d'\wedge l) = (v"+2d')\wedge l \\ &\leq (z+d')\wedge l = (z \wedge l) + (d'\wedge l) \leq w + (d'\wedge l). \end{align*} $$
$$ \begin{align*} v" + 2(d'\wedge l) &= (v" \wedge l) + 2(d'\wedge l) = (v"+2d')\wedge l \\ &\leq (z+d')\wedge l = (z \wedge l) + (d'\wedge l) \leq w + (d'\wedge l). \end{align*} $$
We also have
![]() $d'\wedge l\leq (Mz)\wedge l = M(z\wedge l)\leq Mw$
, and this implies that
$d'\wedge l\leq (Mz)\wedge l = M(z\wedge l)\leq Mw$
, and this implies that
Now, since
![]() $v'\ll v"$
and
$v'\ll v"$
and
![]() $\frac {k}{k+1}<1$
, we can apply [Reference Robert32, Lemma 2.2.5] to obtain
$\frac {k}{k+1}<1$
, we can apply [Reference Robert32, Lemma 2.2.5] to obtain
Since w is strongly soft and
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup, there exists a
$\mathrm {Cu}$
-semigroup, there exists a
![]() $\ll $
-increasing sequence of soft elements with supremum w. Using that the rank map
$\ll $
-increasing sequence of soft elements with supremum w. Using that the rank map
![]() $x\mapsto \widehat {x}$
preserves suprema of increasing sequences, we can find
$x\mapsto \widehat {x}$
preserves suprema of increasing sequences, we can find
![]() $w' \in S_{\mathrm {{soft}}}$
such that
$w' \in S_{\mathrm {{soft}}}$
such that
Further, we have
![]() $w'\ll w\ll x$
. This shows that
$w'\ll w\ll x$
. This shows that
![]() $w'$
is a strongly soft element in
$w'$
is a strongly soft element in
![]() $L_x$
, as desired.
$L_x$
, as desired.
If, additionally, S is left-soft separative, we can apply Lemma 4.4 on (3) to obtain that
![]() $v"+d \leq z$
, and so
$v"+d \leq z$
, and so
![]() $v" \leq z$
. We also have
$v" \leq z$
. We also have
![]() $v" \leq l$
and thus
$v" \leq l$
and thus
We also have
![]() $u' \ll u" \leq w$
and
$u' \ll u" \leq w$
and
![]() $x' \ll \infty w$
. Using that w is strongly soft and that
$x' \ll \infty w$
. Using that w is strongly soft and that
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup, we can find
$\mathrm {Cu}$
-semigroup, we can find
![]() $w' \in S_{\mathrm {{soft}}}$
such that
$w' \in S_{\mathrm {{soft}}}$
such that
![]() $u',v' \ll w' \ll w$
and
$u',v' \ll w' \ll w$
and
![]() $x' \ll \infty w'$
. Then
$x' \ll \infty w'$
. Then
![]() $w'$
has the desired properties.
$w'$
has the desired properties.
Remark 5.4. The assumption of S being countably based in Lemma 5.3 is only used to prove the existence of the infimum
![]() $z\wedge l$
. If S is the Cuntz semigroup of a
$z\wedge l$
. If S is the Cuntz semigroup of a
![]() $\mathrm {C}^*$
-algebra, this infimum always exists; see [Reference Ciuperca, Robert and Santiago16]. Thus, the first part of Lemma 5.3 holds for every
$\mathrm {C}^*$
-algebra, this infimum always exists; see [Reference Ciuperca, Robert and Santiago16]. Thus, the first part of Lemma 5.3 holds for every
![]() $\mathrm {C}^*$
-algebra with the global Glimm property.
$\mathrm {C}^*$
-algebra with the global Glimm property.
Proposition 5.5. Let S be a countably based,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), let
![]() $x',x\in S$
with
$x',x\in S$
with
![]() $x' \ll x$
, let
$x' \ll x$
, let
![]() $k \in {\mathbb {N}}$
and let
$k \in {\mathbb {N}}$
and let
![]() $u' \in L_x$
. Then, for every finite subset
$u' \in L_x$
. Then, for every finite subset
![]() $C\subseteq L_x$
, there exists a strongly soft element
$C\subseteq L_x$
, there exists a strongly soft element
![]() $w'\in L_x$
such that
$w'\in L_x$
such that
for every
![]() $v'\in C$
.
$v'\in C$
.
Proof. We will prove the result by induction on
![]() $\vert C\vert $
, the size of C. If
$\vert C\vert $
, the size of C. If
![]() $\vert C\vert =1$
, the result follows from Lemma 5.3.
$\vert C\vert =1$
, the result follows from Lemma 5.3.
Thus, fix
![]() $n\in {\mathbb {N}}$
with
$n\in {\mathbb {N}}$
with
![]() $n \geq 2$
, and assume that the result holds for any finite subset of
$n \geq 2$
, and assume that the result holds for any finite subset of
![]() $n-1$
elements. Given
$n-1$
elements. Given
![]() $C\subseteq L_x$
with
$C\subseteq L_x$
with
![]() $\vert C\vert =n$
, pick some
$\vert C\vert =n$
, pick some
![]() $v_0\in C$
. Applying the induction hypothesis, we get an element
$v_0\in C$
. Applying the induction hypothesis, we get an element
![]() $w"\in L_x$
such that
$w"\in L_x$
such that
for every
![]() $v'\in C \setminus \{v_0\}$
.
$v'\in C \setminus \{v_0\}$
.
Now, applying Lemma 5.3 to
![]() $x'$
,
$x'$
,
![]() $w"$
and
$w"$
and
![]() $v_0$
, we get a strongly soft element
$v_0$
, we get a strongly soft element
![]() $w' \in L_x$
such that
$w' \in L_x$
such that
Then
![]() $\widehat {w"}\leq \widehat {w'}$
, which shows that
$\widehat {w"}\leq \widehat {w'}$
, which shows that
![]() $w'$
satisfies the required conditions.
$w'$
satisfies the required conditions.
Proposition 5.6. Let S be a countably based,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), let
![]() $x \in S$
and let
$x \in S$
and let
![]() $u' \in L_x$
. Then there exists
$u' \in L_x$
. Then there exists
![]() $w\in S_{\mathrm {{soft}}}$
such that
$w\in S_{\mathrm {{soft}}}$
such that
for every
![]() $\lambda \in F(S)$
.
$\lambda \in F(S)$
.
Proof. By definition of
![]() $L_x$
, we obtain
$L_x$
, we obtain
![]() $u \in S_{\mathrm {{soft}}}$
such that
$u \in S_{\mathrm {{soft}}}$
such that
![]() $u' \ll u \ll x$
. Let
$u' \ll u \ll x$
. Let
![]() $(x_n)_n$
be a
$(x_n)_n$
be a
![]() $\ll $
-increasing sequence with supremum x and such that
$\ll $
-increasing sequence with supremum x and such that
![]() $u \ll x_0$
. Note that the sets
$u \ll x_0$
. Note that the sets
![]() $L_{x_n}$
form an increasing sequence of subsets of S with
$L_{x_n}$
form an increasing sequence of subsets of S with
![]() $L_x = \bigcup _n L_{x_n}$
.
$L_x = \bigcup _n L_{x_n}$
.
Let B be a countable basis for S. Then
and we can choose a
![]() $\subseteq $
-increasing sequence
$\subseteq $
-increasing sequence
![]() $(C_n)_n$
of finite subsets of
$(C_n)_n$
of finite subsets of
![]() $B \cap L_x$
such that
$B \cap L_x$
such that
We have
![]() $u'\in L_{x_0} \subseteq L_{x_1}$
. Apply Proposition 5.5 to
$u'\in L_{x_0} \subseteq L_{x_1}$
. Apply Proposition 5.5 to
![]() $k=1,(0 \ll x_1),u'$
, and
$k=1,(0 \ll x_1),u'$
, and
![]() $C_1$
to obtain a strongly soft element
$C_1$
to obtain a strongly soft element
![]() $w_1'\in L_{x_1}$
such that
$w_1'\in L_{x_1}$
such that
for every
![]() $v' \in C_1$
.
$v' \in C_1$
.
We have
![]() $w_1' \in L_{x_2}$
. Applying Proposition 5.5 again to
$w_1' \in L_{x_2}$
. Applying Proposition 5.5 again to
![]() $k=2,(x_1 \ll x_2),w_1'$
and
$k=2,(x_1 \ll x_2),w_1'$
and
![]() $C_2$
, we obtain a strongly soft element
$C_2$
, we obtain a strongly soft element
![]() $w_2' \in L_{x_2}$
such that
$w_2' \in L_{x_2}$
such that
for every
![]() $v'\in C_2$
.
$v'\in C_2$
.
Proceeding inductively, we get a
![]() $\ll $
-increasing sequence of strongly soft elements
$\ll $
-increasing sequence of strongly soft elements
![]() $(w_n')_n$
such that
$(w_n')_n$
such that
for every
![]() $v'\in C_n$
and
$v'\in C_n$
and
![]() $n \geq 2$
.
$n \geq 2$
.
Set
![]() $w:=\sup _n w_n'$
, which is strongly soft by [Reference Thiel and Vilalta40, Theorem 4.14]. Note that we get
$w:=\sup _n w_n'$
, which is strongly soft by [Reference Thiel and Vilalta40, Theorem 4.14]. Note that we get
![]() $u' \ll w_1' \leq w \leq x$
by construction. Further, since
$u' \ll w_1' \leq w \leq x$
by construction. Further, since
![]() $x_n\leq \infty w_{n+1}'\leq \infty w$
for each
$x_n\leq \infty w_{n+1}'\leq \infty w$
for each
![]() $n \geq 2$
, we deduce that
$n \geq 2$
, we deduce that
![]() $x\leq \infty w$
.
$x\leq \infty w$
.
Now, take
![]() $\lambda \in F(S)$
. Given
$\lambda \in F(S)$
. Given
![]() $v'\in B \cap L_x$
, choose
$v'\in B \cap L_x$
, choose
![]() $n_0 \geq 2$
such that
$n_0 \geq 2$
such that
![]() $v' \in C_{n_0}$
. We have
$v' \in C_{n_0}$
. We have
for every
![]() $n\geq n_0$
. Thus, it follows that
$n\geq n_0$
. Thus, it follows that
![]() $\lambda (v') \leq \lambda (w)$
for every
$\lambda (v') \leq \lambda (w)$
for every
![]() $v' \in B \cap L_x$
.
$v' \in B \cap L_x$
.
Since
![]() $L_x$
is downward hereditary, every element in
$L_x$
is downward hereditary, every element in
![]() $L_x$
is the supremum of an increasing sequence from
$L_x$
is the supremum of an increasing sequence from
![]() $B \cap L_x$
. Using also that functionals preserve suprema of increasing sequences, we obtain
$B \cap L_x$
. Using also that functionals preserve suprema of increasing sequences, we obtain
which shows that w has the desired properties.
Lemma 5.7. Let S be a
![]() $(2, \omega )$
-divisible
$(2, \omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
![]() $x',x,t\in S$
be such that
$x',x,t\in S$
be such that
![]() $x'\ll x\leq \infty t$
. Then there exists a strongly soft element
$x'\ll x\leq \infty t$
. Then there exists a strongly soft element
![]() $u'\in L_x$
such that
$u'\in L_x$
such that
Proof. Choose
![]() $x" \in S$
such that
$x" \in S$
such that
![]() $x'\ll x"\ll x$
. Applying [Reference Thiel and Vilalta43, Proposition 4.10] to
$x'\ll x"\ll x$
. Applying [Reference Thiel and Vilalta43, Proposition 4.10] to
we get
![]() $s\in S$
such that
$s\in S$
such that
By [Reference Thiel and Vilalta40, Proposition 7.7], we can choose
![]() $s'\in S_{\mathrm {{soft}}} $
such that
$s'\in S_{\mathrm {{soft}}} $
such that
Then
![]() $x" \ll \infty s'$
. Applying (O5) to
$x" \ll \infty s'$
. Applying (O5) to
![]() $s'\ll s\leq x$
, we obtain
$s'\ll s\leq x$
, we obtain
![]() $v\in S$
satisfying
$v\in S$
satisfying
In particular, one has
![]() $x"\ll v+s$
. Applying (O6) to
$x"\ll v+s$
. Applying (O6) to
![]() $x' \ll x" \leq v+s$
, we find
$x' \ll x" \leq v+s$
, we find
![]() $u\in S$
such that
$u\in S$
such that
Since
![]() $u\ll x"\leq \infty s'$
, it follows from [Reference Thiel and Vilalta40, Theorem 4.14] that
$u\ll x"\leq \infty s'$
, it follows from [Reference Thiel and Vilalta40, Theorem 4.14] that
![]() $u+s'$
is soft. Further, we get
$u+s'$
is soft. Further, we get
Using that
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup by Proposition 3.6, we can find
$\mathrm {Cu}$
-semigroup by Proposition 3.6, we can find
![]() $u'\in S_{\mathrm {{soft}}}$
such that
$u'\in S_{\mathrm {{soft}}}$
such that
Then
![]() $u'\in L_x$
, which shows that
$u'\in L_x$
, which shows that
![]() $u'$
has the desired properties.
$u'$
has the desired properties.
Lemma 5.8. Let S be a
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
![]() $t\in S_{\mathrm {{soft}}}$
and
$t\in S_{\mathrm {{soft}}}$
and
![]() $t',x',x\in S$
be such that
$t',x',x\in S$
be such that
Then, there exists a strongly soft element
![]() $v'\in L_x$
such that
$v'\in L_x$
such that
Proof. By [Reference Thiel and Vilalta40, Proposition 4.13], there exists
![]() $s\in S_{\mathrm {{soft}}}$
such that
$s\in S_{\mathrm {{soft}}}$
such that
Applying Lemma 5.7 to
![]() $x'\ll x\leq \infty s$
, we obtain a strongly soft element
$x'\ll x\leq \infty s$
, we obtain a strongly soft element
![]() $v'\in L_x$
satisfying
$v'\in L_x$
satisfying
![]() $x'\leq v'+s$
. Consequently, we obtain
$x'\leq v'+s$
. Consequently, we obtain
We refer to [Reference Thiel and Vilalta38, Section 5] for an introduction to the basic technique to reduce certain proofs about
![]() $\mathrm {Cu}$
-semigroups to the countably based setting. In particular, a property
$\mathrm {Cu}$
-semigroups to the countably based setting. In particular, a property
![]() $\mathcal {P}$
for
$\mathcal {P}$
for
![]() $\mathrm {Cu}$
-semigroups is said to satisfy the Löwenheim–Skolem condition if, for every
$\mathrm {Cu}$
-semigroups is said to satisfy the Löwenheim–Skolem condition if, for every
![]() $\mathrm {Cu}$
-semigroup S satisfying
$\mathrm {Cu}$
-semigroup S satisfying
![]() $\mathcal {P}$
, there exists a
$\mathcal {P}$
, there exists a
![]() $\sigma $
-complete and cofinal subcollection of countably based sub-
$\sigma $
-complete and cofinal subcollection of countably based sub-
![]() $\mathrm {Cu}$
-semigroups of S satisfying
$\mathrm {Cu}$
-semigroups of S satisfying
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Lemma 5.9. Let S be a
![]() $\mathrm {Cu}$
-semigroup, let
$\mathrm {Cu}$
-semigroup, let
![]() $u \in S_{\mathrm {{soft}}}$
and let
$u \in S_{\mathrm {{soft}}}$
and let
![]() $\mathcal {R}$
be the family of countably based sub-
$\mathcal {R}$
be the family of countably based sub-
![]() $\mathrm {Cu}$
-semigroups
$\mathrm {Cu}$
-semigroups
![]() $T \subseteq S$
containing u and such that u is strongly soft in T. Then
$T \subseteq S$
containing u and such that u is strongly soft in T. Then
![]() $\mathcal {R}$
is
$\mathcal {R}$
is
![]() $\sigma $
-complete and cofinal.
$\sigma $
-complete and cofinal.
Proof. Strong softness is preserved under
![]() $\mathrm {Cu}$
-morphisms, and the inclusion map of a sub-
$\mathrm {Cu}$
-morphisms, and the inclusion map of a sub-
![]() $\mathrm {Cu}$
-semigroup is a
$\mathrm {Cu}$
-semigroup is a
![]() $\mathrm {Cu}$
-morphism. Hence, given sub-
$\mathrm {Cu}$
-morphism. Hence, given sub-
![]() $\mathrm {Cu}$
-semigroups
$\mathrm {Cu}$
-semigroups
![]() $T_1 \subseteq T_2 \subseteq S$
containing u, if u is strongly soft in
$T_1 \subseteq T_2 \subseteq S$
containing u, if u is strongly soft in
![]() $T_1$
, then it is also strongly soft in
$T_1$
, then it is also strongly soft in
![]() $T_2$
. This implies in particular that
$T_2$
. This implies in particular that
![]() $\mathcal {R}$
is
$\mathcal {R}$
is
![]() $\sigma $
-complete.
$\sigma $
-complete.
To show that
![]() $\mathcal {R}$
is cofinal, let
$\mathcal {R}$
is cofinal, let
![]() $T_0 \subseteq S$
be a countably based sub-
$T_0 \subseteq S$
be a countably based sub-
![]() $\mathrm {Cu}$
-semigroup, and let
$\mathrm {Cu}$
-semigroup, and let
![]() $B_0 \subseteq T_0$
be a countable basis, that is, a countable subset such that every element in
$B_0 \subseteq T_0$
be a countable basis, that is, a countable subset such that every element in
![]() $T_0$
is the supremum of an increasing sequence from
$T_0$
is the supremum of an increasing sequence from
![]() $B_0$
.
$B_0$
.
Let
![]() $(u_n)_n$
be a
$(u_n)_n$
be a
![]() $\ll $
-increasing sequence in S with supremum u. Since u is strongly soft in S, for each n we obtain
$\ll $
-increasing sequence in S with supremum u. Since u is strongly soft in S, for each n we obtain
![]() $t_n \in S$
such that
$t_n \in S$
such that
By [Reference Thiel and Vilalta38, Lemma 5.1], there exists a countably based sub-
![]() $\mathrm {Cu}$
-semigroup
$\mathrm {Cu}$
-semigroup
![]() $T \subseteq S$
containing
$T \subseteq S$
containing
One checks that
![]() $T_0 \subseteq T$
, and that u is strongly soft in T.
$T_0 \subseteq T$
, and that u is strongly soft in T.
Theorem 5.10. Let S be a
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), let
![]() $x\in S$
and let
$x\in S$
and let
![]() $u'\in L_x$
. Then there exists
$u'\in L_x$
. Then there exists
![]() $w\in S_{\mathrm {{soft}}}$
such that
$w\in S_{\mathrm {{soft}}}$
such that
Proof. We first prove the result under the additional assumption that S is countably based. Use Proposition 5.6 to obtain
![]() $w\in S_{\mathrm {{soft}}}$
such that
$w\in S_{\mathrm {{soft}}}$
such that
for every
![]() $\lambda \in F(S)$
. Since
$\lambda \in F(S)$
. Since
![]() $w\leq x$
, we have
$w\leq x$
, we have
![]() $\widehat {w} \leq \widehat {x}$
. To show the reverse inequality, let
$\widehat {w} \leq \widehat {x}$
. To show the reverse inequality, let
![]() $\lambda \in F(S)$
. We need to prove that
$\lambda \in F(S)$
. We need to prove that
![]() $\lambda (x) \leq \lambda (w)$
.
$\lambda (x) \leq \lambda (w)$
.
Take
![]() $x',w'\in S$
such that
$x',w'\in S$
such that
![]() $x' \ll x$
and
$x' \ll x$
and
![]() $w'\ll w$
. Applying Lemma 5.8, we obtain an element
$w'\ll w$
. Applying Lemma 5.8, we obtain an element
![]() $v'\in L_x$
such that
$v'\in L_x$
such that
Since
![]() $v'$
belongs to
$v'$
belongs to
![]() $L_x$
, we have
$L_x$
, we have
![]() $\lambda (v')\leq \lambda (w)$
. This implies
$\lambda (v')\leq \lambda (w)$
. This implies
Passing to the supremum over all
![]() $x'$
way below x, and all
$x'$
way below x, and all
![]() $w'$
way below w, we get
$w'$
way below w, we get
This proves
![]() $\lambda (x)\leq \lambda (w)$
. Indeed, if
$\lambda (x)\leq \lambda (w)$
. Indeed, if
![]() $\lambda (w)=\infty $
, then there is nothing to prove. If
$\lambda (w)=\infty $
, then there is nothing to prove. If
![]() $\lambda (w)\neq \infty $
, we can cancel
$\lambda (w)\neq \infty $
, we can cancel
![]() $\lambda (w)$
from the previous inequality.
$\lambda (w)$
from the previous inequality.
We now consider the case that S is not countably based. Choose
![]() $u \in S_{\mathrm {{soft}}}$
such that
$u \in S_{\mathrm {{soft}}}$
such that
![]() $u' \ll u \ll x$
. Since
$u' \ll u \ll x$
. Since
![]() $(2,\omega )$
-divisibility and (O5)–(O7) each satisfy the Löwenheim-Skolem condition, and using also Lemma 5.9, we can use the technique from [Reference Thiel and Vilalta38, Section 5] to deduce that there exists a countably based,
$(2,\omega )$
-divisibility and (O5)–(O7) each satisfy the Löwenheim-Skolem condition, and using also Lemma 5.9, we can use the technique from [Reference Thiel and Vilalta38, Section 5] to deduce that there exists a countably based,
![]() $(2,\omega )$
-divisible sub-
$(2,\omega )$
-divisible sub-
![]() $\mathrm {Cu}$
-semigroup
$\mathrm {Cu}$
-semigroup
![]() $H \subseteq S$
satisfying (O5)–(O7), containing x, u and
$H \subseteq S$
satisfying (O5)–(O7), containing x, u and
![]() $u'$
, and such that u is strongly soft in H.
$u'$
, and such that u is strongly soft in H.
Applying the first part of the proof to H, we find
![]() $w\in H_{\mathrm {{soft}}}$
such that
$w\in H_{\mathrm {{soft}}}$
such that
for every
![]() $\lambda \in F(H)$
.
$\lambda \in F(H)$
.
Since the inclusion
![]() $\iota \colon H\to S$
is a
$\iota \colon H\to S$
is a
![]() $\mathrm {Cu}$
-morphism, it follows that w is strongly soft in S. Further, any functional
$\mathrm {Cu}$
-morphism, it follows that w is strongly soft in S. Further, any functional
![]() $\lambda $
on S induces the functional
$\lambda $
on S induces the functional
![]() $\lambda \iota $
on H. This shows that w satisfies the required conditions.
$\lambda \iota $
on H. This shows that w satisfies the required conditions.
Theorem 5.11. Let A be a stable
![]() $\mathrm {C}^*$
-algebra with the global Glimm property. Then, for any
$\mathrm {C}^*$
-algebra with the global Glimm property. Then, for any
![]() $a\in A_+$
there exists a soft element
$a\in A_+$
there exists a soft element
![]() $b \in A_+$
with
$b \in A_+$
with
![]() $b\precsim a$
and such that
$b\precsim a$
and such that
for every
![]() $\tau \in {\mathrm {QT}}(A)$
.
$\tau \in {\mathrm {QT}}(A)$
.
Proof. Let
![]() $a\in A_+$
. Since A has the global Glimm property, it follows from [Reference Thiel and Vilalta43, Theorem 3.6] that
$a\in A_+$
. Since A has the global Glimm property, it follows from [Reference Thiel and Vilalta43, Theorem 3.6] that
![]() $ {\mathrm {Cu}} (A)$
is
$ {\mathrm {Cu}} (A)$
is
![]() $(2,\omega )$
-divisible. Using Theorem 5.10, find
$(2,\omega )$
-divisible. Using Theorem 5.10, find
![]() $w\in {\mathrm {Cu}} (A)_{\mathrm {{soft}}}$
such that
$w\in {\mathrm {Cu}} (A)_{\mathrm {{soft}}}$
such that
![]() $w\leq [a]$
and
$w\leq [a]$
and
![]() $\lambda (w)=\lambda ([a])$
for every
$\lambda (w)=\lambda ([a])$
for every
![]() $\lambda \in F( {\mathrm {Cu}} (A))$
.
$\lambda \in F( {\mathrm {Cu}} (A))$
.
By Theorem 3.3, there exists a soft element
![]() $b\in A_+$
such that
$b\in A_+$
such that
![]() $w=[b]$
. The result now follows from the fact that the map
$w=[b]$
. The result now follows from the fact that the map
is a natural bijection from
![]() $\mathrm {QT} (A)$
to
$\mathrm {QT} (A)$
to
![]() $F( {\mathrm {Cu}} (A))$
; see [Reference Elliott, Robert and Santiago20, Theorem 4.4].
$F( {\mathrm {Cu}} (A))$
; see [Reference Elliott, Robert and Santiago20, Theorem 4.4].
Lemma 5.12. Let S be a
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup S satisfying (O5), let
$\mathrm {Cu}$
-semigroup S satisfying (O5), let
![]() $x\in S$
and let
$x\in S$
and let
![]() $\lambda \in F(S)$
. Then
$\lambda \in F(S)$
. Then
Proof. Given
![]() $v' \in L_x$
, there exists
$v' \in L_x$
, there exists
![]() $v \in S_{\mathrm {{soft}}}$
with
$v \in S_{\mathrm {{soft}}}$
with
![]() $v' \leq v \leq x$
, which shows the inequality ‘
$v' \leq v \leq x$
, which shows the inequality ‘
![]() $\geq $
’.
$\geq $
’.
Conversely, let
![]() $v \in S_{\mathrm {{soft}}}$
with
$v \in S_{\mathrm {{soft}}}$
with
![]() $v \leq x$
. Since
$v \leq x$
. Since
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup by Proposition 3.6, there exists a
$\mathrm {Cu}$
-semigroup by Proposition 3.6, there exists a
![]() $\ll $
-increasing sequence
$\ll $
-increasing sequence
![]() $(v_n')_n$
in
$(v_n')_n$
in
![]() $S_{\mathrm {{soft}}}$
with supremum v. Each
$S_{\mathrm {{soft}}}$
with supremum v. Each
![]() $v_n'$
belongs to
$v_n'$
belongs to
![]() $L_x$
, and one gets
$L_x$
, and one gets
This shows the the inequality ‘
![]() $\leq $
’.
$\leq $
’.
We will prove in Theorem 5.14 that the inclusion
![]() $\iota \colon S_{\mathrm {{soft}}}\to S$
induces a homeomorphism
$\iota \colon S_{\mathrm {{soft}}}\to S$
induces a homeomorphism
![]() $\iota ^*\colon F(S)\to F(S_{\mathrm {{soft}}})$
. The inverse of
$\iota ^*\colon F(S)\to F(S_{\mathrm {{soft}}})$
. The inverse of
![]() $\iota ^*$
is constructed in the next result.
$\iota ^*$
is constructed in the next result.
Proposition 5.13. Let S be a
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
![]() $\lambda \in F(S_{\mathrm {{soft}}} )$
. Then
$\lambda \in F(S_{\mathrm {{soft}}} )$
. Then
![]() $\lambda _{\mathrm {{soft}}} \colon S \to [0,\infty ]$
given by
$\lambda _{\mathrm {{soft}}} \colon S \to [0,\infty ]$
given by
for
![]() $x \in S$
, is a functional on S.
$x \in S$
, is a functional on S.
Proof. It is easy to see that
![]() $\lambda _{\mathrm {{soft}}}$
preserves order. Further, given an increasing sequence
$\lambda _{\mathrm {{soft}}}$
preserves order. Further, given an increasing sequence
![]() $(x_n)_n$
with supremum x in S, we have that for every
$(x_n)_n$
with supremum x in S, we have that for every
![]() $v'\in L_x$
there exists
$v'\in L_x$
there exists
![]() $n\in {\mathbb {N}}$
with
$n\in {\mathbb {N}}$
with
![]() $v'\in L_{x_n}$
. Thus, using Lemma 5.12, we get
$v'\in L_{x_n}$
. Thus, using Lemma 5.12, we get
 $$\begin{align*}\lambda_{\mathrm{{soft}}} (x) = \sup_{v'\in L_x}\lambda (v') \leq \sup_n \left(\sup_{v'\in L_{x_n}}\lambda (v') \right) =\sup_n \lambda_{\mathrm{{soft}}} (x_n). \end{align*}$$
$$\begin{align*}\lambda_{\mathrm{{soft}}} (x) = \sup_{v'\in L_x}\lambda (v') \leq \sup_n \left(\sup_{v'\in L_{x_n}}\lambda (v') \right) =\sup_n \lambda_{\mathrm{{soft}}} (x_n). \end{align*}$$
Since
![]() $\lambda _{\mathrm {{soft}}}$
is order preserving, we also have
$\lambda _{\mathrm {{soft}}}$
is order preserving, we also have
![]() $\sup _n \lambda _{\mathrm {{soft}}} (x_n)\leq \lambda _{\mathrm {{soft}}} (x)$
, which shows that
$\sup _n \lambda _{\mathrm {{soft}}} (x_n)\leq \lambda _{\mathrm {{soft}}} (x)$
, which shows that
![]() $\lambda _{\mathrm {{soft}}}$
preserves suprema of increasing sequences.
$\lambda _{\mathrm {{soft}}}$
preserves suprema of increasing sequences.
Given
![]() $x,y\in S$
and
$x,y\in S$
and
![]() $u,v\in S_{\mathrm {{soft}}}$
such that
$u,v\in S_{\mathrm {{soft}}}$
such that
![]() $u\leq x$
and
$u\leq x$
and
![]() $v\leq y$
, we have
$v\leq y$
, we have
![]() $u+v\in S_{\mathrm {{soft}}}$
and
$u+v\in S_{\mathrm {{soft}}}$
and
![]() $u+v\leq x+y$
. This implies that
$u+v\leq x+y$
. This implies that
Thus,
![]() $\lambda _{\mathrm {{soft}}}$
is subadditive.
$\lambda _{\mathrm {{soft}}}$
is subadditive.
Finally, we show that
![]() $\lambda _{\mathrm {{soft}}}$
is superadditive. Given
$\lambda _{\mathrm {{soft}}}$
is superadditive. Given
![]() $x,y\in S$
and
$x,y\in S$
and
![]() $w'\in L_{x+y}$
, take
$w'\in L_{x+y}$
, take
![]() $x',x",y',y"\in S$
such that
$x',x",y',y"\in S$
such that
By [Reference Thiel and Vilalta40, Proposition 7.7], there exist
![]() $s,t\in S_{\mathrm {{soft}}}$
such that
$s,t\in S_{\mathrm {{soft}}}$
such that
Take
![]() $s',t'\in S$
such that
$s',t'\in S$
such that
![]() $s'\ll s$
and
$s'\ll s$
and
![]() $t'\ll t$
. Using Lemma 5.8, we find
$t'\ll t$
. Using Lemma 5.8, we find
![]() $u'\in L_x$
and
$u'\in L_x$
and
![]() $v'\in L_y$
such that
$v'\in L_y$
such that
Consequently, one has
Applying Theorem 5.10, find
![]() $u,v\in S_{\mathrm {{soft}}}$
such that
$u,v\in S_{\mathrm {{soft}}}$
such that
This implies
and, therefore,
Passing to the suprema over all
![]() $s'$
way below s, and all
$s'$
way below s, and all
![]() $t'$
way below t, we deduce that
$t'$
way below t, we deduce that
Note that
![]() $s+t\leq x"+y" \ll x+y \leq \infty (u+v)$
. This allows us to cancel
$s+t\leq x"+y" \ll x+y \leq \infty (u+v)$
. This allows us to cancel
![]() $\lambda (s + t)$
, and we obtain
$\lambda (s + t)$
, and we obtain
Since this holds for every
![]() $w'\in L_{x+y}$
, we can apply Lemma 5.12 to get
$w'\in L_{x+y}$
, we can apply Lemma 5.12 to get
This show that
![]() $\lambda _{\mathrm {{soft}}}$
is superadditive and thus a functional.
$\lambda _{\mathrm {{soft}}}$
is superadditive and thus a functional.
Theorem 5.14. Let S be a
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Let
![]() $\iota \colon S_{\mathrm {{soft}}}\to S$
be the canonical inclusion. Then the map
$\iota \colon S_{\mathrm {{soft}}}\to S$
be the canonical inclusion. Then the map
![]() $\iota ^*\colon F(S)\to F(S_{\mathrm {{soft}}})$
given by
$\iota ^*\colon F(S)\to F(S_{\mathrm {{soft}}})$
given by
![]() $\iota ^*(\lambda ):=\lambda \circ \iota $
is a natural homeomorphism.
$\iota ^*(\lambda ):=\lambda \circ \iota $
is a natural homeomorphism.
Proof. Given
![]() $\lambda \in F(S_{\mathrm {{soft}}})$
, let
$\lambda \in F(S_{\mathrm {{soft}}})$
, let
![]() $\lambda _{\mathrm {{soft}}} \in F(S)$
be defined as in Proposition 5.13. This defines a map
$\lambda _{\mathrm {{soft}}} \in F(S)$
be defined as in Proposition 5.13. This defines a map
![]() $\phi \colon F(S_{\mathrm {{soft}}} )\to F(S)$
by
$\phi \colon F(S_{\mathrm {{soft}}} )\to F(S)$
by
![]() $\phi (\lambda ) :=\lambda _{\mathrm {{soft}}}$
. We verify that
$\phi (\lambda ) :=\lambda _{\mathrm {{soft}}}$
. We verify that
![]() $\iota ^*\phi ={\operatorname{id}}_{F(S_{\mathrm {{soft}}} )}$
and
$\iota ^*\phi ={\operatorname{id}}_{F(S_{\mathrm {{soft}}} )}$
and
![]() $\phi \iota ^*={\operatorname {id}}_{F(S)}$
.
$\phi \iota ^*={\operatorname {id}}_{F(S)}$
.
Given
![]() $\lambda \in F(S_{\mathrm {{soft}}} )$
and
$\lambda \in F(S_{\mathrm {{soft}}} )$
and
![]() $w\in S_{\mathrm {{soft}}}$
, we have
$w\in S_{\mathrm {{soft}}}$
, we have
which shows
![]() $\iota ^*\phi ={\operatorname {id}}_{F(S_{\mathrm {{soft}}} )}$
.
$\iota ^*\phi ={\operatorname {id}}_{F(S_{\mathrm {{soft}}} )}$
.
Conversely, if
![]() $\lambda \in F(S)$
and
$\lambda \in F(S)$
and
![]() $x\in S$
, we can use Theorem 5.10 at the last step to obtain
$x\in S$
, we can use Theorem 5.10 at the last step to obtain
This shows that
![]() $\iota ^*$
is a bijective, continuous map. Since
$\iota ^*$
is a bijective, continuous map. Since
![]() $F(S)$
and
$F(S)$
and
![]() $F(S)_{\mathrm {{soft}}}$
are both compact, Hausdorff spaces, it follows that
$F(S)_{\mathrm {{soft}}}$
are both compact, Hausdorff spaces, it follows that
![]() $\iota ^*$
is a homeomorphism.
$\iota ^*$
is a homeomorphism.
Since simple, nonelementary
![]() $\mathrm {C}^*$
-algebras automatically have the global Glimm property, the next result can be considered as a generalization of [Reference Phillips31, Lemma 3.8] to the nonsimple setting.
$\mathrm {C}^*$
-algebras automatically have the global Glimm property, the next result can be considered as a generalization of [Reference Phillips31, Lemma 3.8] to the nonsimple setting.
Theorem 5.15. Let A be a
![]() $\mathrm {C}^*$
-algebra with the global Glimm property. Then
$\mathrm {C}^*$
-algebra with the global Glimm property. Then
![]() $ {\mathrm {QT}}(A)$
is naturally homeomorphic to
$ {\mathrm {QT}}(A)$
is naturally homeomorphic to
![]() $F( {\mathrm {Cu}} (A)_{\mathrm {{soft}}} )$
.
$F( {\mathrm {Cu}} (A)_{\mathrm {{soft}}} )$
.
Proof. The result follows from Theorem 5.14 and the fact that
![]() $ {\mathrm {QT}}(A)$
is naturally homeomorphic to
$ {\mathrm {QT}}(A)$
is naturally homeomorphic to
![]() $F( {\mathrm {Cu}} (A))$
; see [Reference Elliott, Robert and Santiago20, Theorem 4.4].
$F( {\mathrm {Cu}} (A))$
; see [Reference Elliott, Robert and Santiago20, Theorem 4.4].
6 Retraction onto the soft part of a Cuntz semigroup
Let S be a countably based, left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Given any
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Given any
![]() $x\in S$
, we have seen in Lemma 5.3 that
$x\in S$
, we have seen in Lemma 5.3 that
![]() $L_x$
is upward directed. It then follows from [Reference Antoine, Perera and Thiel4, Remarks 3.1.3] that
$L_x$
is upward directed. It then follows from [Reference Antoine, Perera and Thiel4, Remarks 3.1.3] that
![]() $L_x$
has a supremum, which justifies the following:
$L_x$
has a supremum, which justifies the following:
Definition 6.1. Let S be a countably based, left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). We define
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). We define
![]() $\sigma \colon S \to S$
by
$\sigma \colon S \to S$
by
for
![]() $x \in S$
.
$x \in S$
.
We will see in Proposition 6.3 that
![]() $\sigma (x)$
is the largest strongly soft element dominated by x. Therefore, we often view
$\sigma (x)$
is the largest strongly soft element dominated by x. Therefore, we often view
![]() $\sigma $
as a map
$\sigma $
as a map
![]() $S \to S_{\mathrm {{soft}}}$
. In Theorem 6.6, we show that
$S \to S_{\mathrm {{soft}}}$
. In Theorem 6.6, we show that
![]() $\sigma $
is close to being a generalized
$\sigma $
is close to being a generalized
![]() $\mathrm {Cu}$
-morphism, and in Proposition 6.8 we give sufficient conditions ensuring that it is.
$\mathrm {Cu}$
-morphism, and in Proposition 6.8 we give sufficient conditions ensuring that it is.
If A is a separable
![]() $\mathrm {C}^*$
-algebra satisfying the global Glimm property and with left-soft separative Cuntz semigroup, then
$\mathrm {C}^*$
-algebra satisfying the global Glimm property and with left-soft separative Cuntz semigroup, then
![]() $ {\mathrm {Cu}}(A)$
satisfies the assumptions of Definition 6.1. If A also has stable rank one or strict comparison of positive elements, then
$ {\mathrm {Cu}}(A)$
satisfies the assumptions of Definition 6.1. If A also has stable rank one or strict comparison of positive elements, then
![]() $\sigma \colon {\mathrm {Cu}}(A) \to {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
is a generalized
$\sigma \colon {\mathrm {Cu}}(A) \to {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
is a generalized
![]() $\mathrm {Cu}$
-morphism; see Theorem 6.9. Then
$\mathrm {Cu}$
-morphism; see Theorem 6.9. Then
![]() $ {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
is a retract of S; see Definition 6.7. This generalizes the construction of predecessors in the context of simple
$ {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
is a retract of S; see Definition 6.7. This generalizes the construction of predecessors in the context of simple
![]() $\mathrm {C}^*$
-algebras from [Reference Engbers22], as well as the constructions from [Reference Antoine, Perera and Thiel4, Section 5.4] and [Reference Thiel37, Proposition 2.9].
$\mathrm {C}^*$
-algebras from [Reference Engbers22], as well as the constructions from [Reference Antoine, Perera and Thiel4, Section 5.4] and [Reference Thiel37, Proposition 2.9].
Remark 6.2. Let S be a weakly cancellative
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7) (for instance, the Cuntz semigroup of a stable rank one
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7) (for instance, the Cuntz semigroup of a stable rank one
![]() $\mathrm {C}^*$
-algebra). Take
$\mathrm {C}^*$
-algebra). Take
![]() $x\in S$
, and consider the set
$x\in S$
, and consider the set
A slight modification of Proposition 5.5 shows that
![]() $L_x'$
is upward directed.
$L_x'$
is upward directed.
If S is countably based and
![]() $(2,\omega )$
-divisible, it is readily checked that
$(2,\omega )$
-divisible, it is readily checked that
However, if S is not
![]() $(2,\omega )$
-divisible,
$(2,\omega )$
-divisible,
![]() $\sup L_x'$
may not be strongly soft. For example, the Cuntz semigroup of
$\sup L_x'$
may not be strongly soft. For example, the Cuntz semigroup of
![]() $\mathbb {C}$
is
$\mathbb {C}$
is
![]() $\overline {{\mathbb {N}}} = {\mathbb {N}}\cup \{\infty \}$
, which is weakly cancellative. One can check that
$\overline {{\mathbb {N}}} = {\mathbb {N}}\cup \{\infty \}$
, which is weakly cancellative. One can check that
 $$\begin{align*}\sup L_x' = \begin{cases} 0, & \text{ if } x=0 \\ x-1, & \text{ if } x\neq 0,\infty \\ \infty, & \text{ if } x=\infty \\ \end{cases}. \end{align*}$$
$$\begin{align*}\sup L_x' = \begin{cases} 0, & \text{ if } x=0 \\ x-1, & \text{ if } x\neq 0,\infty \\ \infty, & \text{ if } x=\infty \\ \end{cases}. \end{align*}$$
In particular, if
![]() $x\neq 0, \infty $
, we get
$x\neq 0, \infty $
, we get
![]() $\sup L_x'=x-1$
, which is not strongly soft.
$\sup L_x'=x-1$
, which is not strongly soft.
As another example, there are
![]() $\mathrm {Cu}$
-semigroups whose order structure is deeply related to its soft elements but where
$\mathrm {Cu}$
-semigroups whose order structure is deeply related to its soft elements but where
![]() $\sup L_x'$
is rarely strongly soft: Let S be a
$\sup L_x'$
is rarely strongly soft: Let S be a
![]() $\mathrm {Cu}$
-semigroup of the form
$\mathrm {Cu}$
-semigroup of the form
![]() $ {\mathrm {Lsc}}(X,\overline {{\mathbb {N}}})$
for some
$ {\mathrm {Lsc}}(X,\overline {{\mathbb {N}}})$
for some
![]() $T_1$
-space X (these were called Lsc-like in [Reference Vilalta46]). An element
$T_1$
-space X (these were called Lsc-like in [Reference Vilalta46]). An element
![]() $f \in {\mathrm {Lsc}}(X,\overline {{\mathbb {N}}})$
is strongly soft if and only if
$f \in {\mathrm {Lsc}}(X,\overline {{\mathbb {N}}})$
is strongly soft if and only if
![]() $f = \infty \chi _U$
for the indicator function
$f = \infty \chi _U$
for the indicator function
![]() $\chi _U$
of some open subset
$\chi _U$
of some open subset
![]() $U \subseteq X$
. Thus, if
$U \subseteq X$
. Thus, if
![]() $x\in S$
satisfies
$x\in S$
satisfies
![]() $x\ll \infty $
, we have
$x\ll \infty $
, we have
![]() $\sup L_x'\ll \infty $
, which implies that
$\sup L_x'\ll \infty $
, which implies that
![]() $\sup L_x'$
is not strongly soft, unless it is zero.
$\sup L_x'$
is not strongly soft, unless it is zero.
Proposition 6.3. Let S be a countably based, left-soft separative,
![]() $(2, \omega )$
-divisible
$(2, \omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
![]() $x\in S$
. Then:
$x\in S$
. Then:
-
(1) The element
 $\sigma (x)$
is the largest strongly soft element dominated by x.
$\sigma (x)$
is the largest strongly soft element dominated by x. -
(2) We have
 $\infty x=\infty \sigma (x)$
.
$\infty x=\infty \sigma (x)$
. -
(3) We have
 $x=\sigma (x)$
if and only if x is strongly soft.
$x=\sigma (x)$
if and only if x is strongly soft. -
(4) We have
 $x\leq \sigma (x)+t$
for all
$x\leq \sigma (x)+t$
for all
 $t \in S$
with
$t \in S$
with
 $x\leq \infty t$
.
$x\leq \infty t$
.
Proof. To verify (1), note that the members of
![]() $L_x$
are bounded by x, and consequently
$L_x$
are bounded by x, and consequently
![]() $\sigma (x) \leq x$
. To see that
$\sigma (x) \leq x$
. To see that
![]() $\sigma (x)$
is strongly soft, let
$\sigma (x)$
is strongly soft, let
![]() $s\in S$
be such that
$s\in S$
be such that
![]() $s\ll \sigma (x)$
. We will find
$s\ll \sigma (x)$
. We will find
![]() $t \in S$
such that
$t \in S$
such that
![]() $s + t \ll \sigma (x)$
and
$s + t \ll \sigma (x)$
and
![]() $s \ll \infty t$
.
$s \ll \infty t$
.
Since
![]() $\sigma (x)=\sup L_x$
, there exists
$\sigma (x)=\sup L_x$
, there exists
![]() $u' \in L_x$
such that
$u' \in L_x$
such that
![]() $s \ll u' \leq \sigma (x)$
. Using that
$s \ll u' \leq \sigma (x)$
. Using that
![]() $u'\in L_x$
, we find
$u'\in L_x$
, we find
![]() $u\in S_{\mathrm {{soft}}}$
with
$u\in S_{\mathrm {{soft}}}$
with
![]() $u'\ll u\ll x$
. By Proposition 3.6,
$u'\ll u\ll x$
. By Proposition 3.6,
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup, and we obtain
$\mathrm {Cu}$
-semigroup, and we obtain
![]() $u" \in S_{\mathrm {{soft}}}$
such that
$u" \in S_{\mathrm {{soft}}}$
such that
Then
![]() $s \ll u" \in S_{\mathrm {{soft}}}$
and by the definition of strong softness we obtain
$s \ll u" \in S_{\mathrm {{soft}}}$
and by the definition of strong softness we obtain
![]() $t \in S$
such that
$t \in S$
such that
![]() $s+t\ll u"$
and
$s+t\ll u"$
and
![]() $s \ll \infty t$
. We have
$s \ll \infty t$
. We have
![]() $u" \in L_x$
and therefore
$u" \in L_x$
and therefore
![]() $u" \leq \sigma (x)$
, which shows that t has the desired properties.
$u" \leq \sigma (x)$
, which shows that t has the desired properties.
Thus,
![]() $\sigma (x)$
is a strongly soft element dominated by x. To show that it is the largest element with these properties, let
$\sigma (x)$
is a strongly soft element dominated by x. To show that it is the largest element with these properties, let
![]() $w \in S_{\mathrm {{soft}}}$
satisfy
$w \in S_{\mathrm {{soft}}}$
satisfy
![]() $w\leq x$
. We can use once again that
$w\leq x$
. We can use once again that
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup to find a
$\mathrm {Cu}$
-semigroup to find a
![]() $\ll $
-increasing sequence
$\ll $
-increasing sequence
![]() $(w_n)_n$
of strongly soft elements with supremum w. Then
$(w_n)_n$
of strongly soft elements with supremum w. Then
![]() $w_n \in L_x$
for each n, and consequently
$w_n \in L_x$
for each n, and consequently
This also shows that
![]() $x=\sigma (x)$
if and only if x is strongly soft. We have proved (1) and (3).
$x=\sigma (x)$
if and only if x is strongly soft. We have proved (1) and (3).
To verify (2), we first note that
![]() $\infty \sigma (x) \leq \infty x$
since
$\infty \sigma (x) \leq \infty x$
since
![]() $\sigma (x) \leq x$
. For the converse inequality, use Proposition 5.6 to obtain
$\sigma (x) \leq x$
. For the converse inequality, use Proposition 5.6 to obtain
![]() $w\in S_{\mathrm {{soft}}}$
with
$w\in S_{\mathrm {{soft}}}$
with
![]() $w\leq x\leq \infty w$
. By (1), we have
$w\leq x\leq \infty w$
. By (1), we have
![]() $w\leq \sigma (x)$
, and we get
$w\leq \sigma (x)$
, and we get
Finally, to prove (4), let
![]() $t \in S$
satisfy
$t \in S$
satisfy
![]() $x \leq \infty t$
. Let
$x \leq \infty t$
. Let
![]() $x' \in S$
satisfy
$x' \in S$
satisfy
![]() $x' \ll x$
. Applying Lemma 5.7, we obtain
$x' \ll x$
. Applying Lemma 5.7, we obtain
![]() $u' \in L_x$
such that
$u' \in L_x$
such that
![]() $x' \ll u'+t$
. Then
$x' \ll u'+t$
. Then
Passing to the supremum over all
![]() $x'$
way below x, we get
$x'$
way below x, we get
![]() $x \leq \sigma (x)+t$
, as desired.
$x \leq \sigma (x)+t$
, as desired.
Example 6.4. Let A be a separable,
![]() $\mathcal {W}$
-stable
$\mathcal {W}$
-stable
![]() $\mathrm {C}^*$
-algebra, that is,
$\mathrm {C}^*$
-algebra, that is,
![]() $A \cong A \otimes \mathcal {W}$
where
$A \cong A \otimes \mathcal {W}$
where
![]() $\mathcal {W}$
denotes the Jacelon–Razak algebra. Then, every element in
$\mathcal {W}$
denotes the Jacelon–Razak algebra. Then, every element in
![]() $ {\mathrm {Cu}} (A)$
is strongly soft. Thus, Proposition 6.3 implies that
$ {\mathrm {Cu}} (A)$
is strongly soft. Thus, Proposition 6.3 implies that
![]() $\sigma (x)=x$
for every
$\sigma (x)=x$
for every
![]() $x\in {\mathrm {Cu}} (A)$
. We refer to [Reference Antoine, Perera and Thiel4, Section 7.5] for details.
$x\in {\mathrm {Cu}} (A)$
. We refer to [Reference Antoine, Perera and Thiel4, Section 7.5] for details.
Similarly, given a separable
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $\mathrm {C}^*$
-algebra A, where
$\mathrm {C}^*$
-algebra A, where
![]() $\mathcal {Z}$
denotes the Jiang–Su algebra, then it follows from [Reference Antoine, Perera and Thiel4, Theorem 7.3.11] that
$\mathcal {Z}$
denotes the Jiang–Su algebra, then it follows from [Reference Antoine, Perera and Thiel4, Theorem 7.3.11] that
![]() $ {\mathrm {Cu}} (A)$
has Z-multiplication. Here,
$ {\mathrm {Cu}} (A)$
has Z-multiplication. Here,
![]() $Z=(0,\infty ]\sqcup {\mathbb {N}}$
is the Cuntz semigroup of
$Z=(0,\infty ]\sqcup {\mathbb {N}}$
is the Cuntz semigroup of
![]() $\mathcal {Z}$
, and
$\mathcal {Z}$
, and
![]() $(0,\infty ]$
is the subsemigroup of nonzero, strongly soft elements. Let
$(0,\infty ]$
is the subsemigroup of nonzero, strongly soft elements. Let
![]() $1' \in Z$
be the strongly soft element corresponding to
$1' \in Z$
be the strongly soft element corresponding to
![]() $1\in [0,\infty ]$
. As noted in [Reference Antoine, Perera and Thiel4, Proposition 7.3.16], one has
$1\in [0,\infty ]$
. As noted in [Reference Antoine, Perera and Thiel4, Proposition 7.3.16], one has
This implies that
![]() $\sigma (x) = 1'x$
for each
$\sigma (x) = 1'x$
for each
![]() $x\in {\mathrm {Cu}} (A)$
.
$x\in {\mathrm {Cu}} (A)$
.
Lemma 6.5. Let S be a countably based, left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
![]() $x\in S$
. Then
$x\in S$
. Then
Proof. Using that
![]() $\sigma (x)\leq x$
, we have
$\sigma (x)\leq x$
, we have
![]() $2\sigma (x)\leq x+\sigma (x)$
. To show the reverse inequality, let
$2\sigma (x)\leq x+\sigma (x)$
. To show the reverse inequality, let
![]() $w \in S$
satisfy
$w \in S$
satisfy
![]() $w\ll \sigma (x)$
. Since
$w\ll \sigma (x)$
. Since
![]() $\sigma (x)$
is strongly soft, it follows from [Reference Thiel and Vilalta40, Proposition 4.13] that there exists
$\sigma (x)$
is strongly soft, it follows from [Reference Thiel and Vilalta40, Proposition 4.13] that there exists
![]() $t\in S$
with
$t\in S$
with
![]() $w+t\leq \sigma (x)\leq \infty t$
.
$w+t\leq \sigma (x)\leq \infty t$
.
We have
![]() $x \leq \infty \sigma (x)$
by Proposition 6.3 (2), and thus
$x \leq \infty \sigma (x)$
by Proposition 6.3 (2), and thus
![]() $x \leq \infty t$
. Therefore,
$x \leq \infty t$
. Therefore,
![]() $x\leq \sigma (x)+t$
by Proposition 6.3 (4). Thus, we have
$x\leq \sigma (x)+t$
by Proposition 6.3 (4). Thus, we have
Passing to the supremum over all w way below
![]() $\sigma (x)$
, we get
$\sigma (x)$
, we get
![]() $x+\sigma (x)\leq 2\sigma (x)$
.
$x+\sigma (x)\leq 2\sigma (x)$
.
Theorem 6.6. Let S be a countably based, left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Then, the map
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Then, the map
![]() $\sigma \colon S\to S_{\mathrm {{soft}}}$
preserves order, suprema of increasing sequences and is superadditive. Further, we have
$\sigma \colon S\to S_{\mathrm {{soft}}}$
preserves order, suprema of increasing sequences and is superadditive. Further, we have
for every
![]() $x,y\in S$
.
$x,y\in S$
.
Proof. To show that
![]() $\sigma $
is order preserving, let
$\sigma $
is order preserving, let
![]() $x,y\in S$
satisfy
$x,y\in S$
satisfy
![]() $x\leq y$
. Then
$x\leq y$
. Then
![]() $L_x \subseteq L_y$
, and thus
$L_x \subseteq L_y$
, and thus
To show that
![]() $\sigma $
preserves suprema of increasing sequences, let
$\sigma $
preserves suprema of increasing sequences, let
![]() $(x_n)_n$
be an increasing sequence in S with supremum x. Since
$(x_n)_n$
be an increasing sequence in S with supremum x. Since
![]() $\sigma $
is order-preserving, one gets
$\sigma $
is order-preserving, one gets
![]() $\sup _n\sigma (x_n) \leq \sigma (x)$
. Conversely, given
$\sup _n\sigma (x_n) \leq \sigma (x)$
. Conversely, given
![]() $u' \in L_x$
, choose
$u' \in L_x$
, choose
![]() $u \in S_{\mathrm {{soft}}}$
with
$u \in S_{\mathrm {{soft}}}$
with
![]() $u' \ll u \ll x$
. Then there exists
$u' \ll u \ll x$
. Then there exists
![]() $n\in {\mathbb {N}}$
such that
$n\in {\mathbb {N}}$
such that
![]() $u \ll x_n$
, and thus
$u \ll x_n$
, and thus
![]() $u' \in L_{x_n}$
. We deduce that
$u' \in L_{x_n}$
. We deduce that
Hence,
![]() $\sigma (x) = \sup L_x \leq \sup _n \sigma (x_n)$
, as desired.
$\sigma (x) = \sup L_x \leq \sup _n \sigma (x_n)$
, as desired.
To see that
![]() $\sigma $
is superadditive, let
$\sigma $
is superadditive, let
![]() $x,y\in S$
. Note that
$x,y\in S$
. Note that
![]() $\sigma (x)+\sigma (y)$
is a strongly soft element bounded by
$\sigma (x)+\sigma (y)$
is a strongly soft element bounded by
![]() $x+y$
. Using Proposition 6.3 (1), we get
$x+y$
. Using Proposition 6.3 (1), we get
![]() $\sigma (x)+\sigma (y)\leq \sigma (x+y)$
.
$\sigma (x)+\sigma (y)\leq \sigma (x+y)$
.
Next, given
![]() $x,y \in S$
, let us show that
$x,y \in S$
, let us show that
![]() $2\sigma (x+y) \leq 2\sigma (x) + 2\sigma (y)$
. To prove this, let
$2\sigma (x+y) \leq 2\sigma (x) + 2\sigma (y)$
. To prove this, let
![]() $w \in S$
satisfy
$w \in S$
satisfy
![]() $w \ll \sigma (x+y)$
. By [Reference Thiel and Vilalta40, Proposition 4.13], there exists
$w \ll \sigma (x+y)$
. By [Reference Thiel and Vilalta40, Proposition 4.13], there exists
![]() $s\in S$
satisfying
$s\in S$
satisfying
Applying [Reference Thiel and Vilalta40, Proposition 7.7], we find
![]() $t \in S$
such that
$t \in S$
such that
![]() $2t \leq s\leq \infty t$
. Using also Proposition 6.3 (2), we deduce that
$2t \leq s\leq \infty t$
. Using also Proposition 6.3 (2), we deduce that
Using Proposition 6.3 (4) at the second step and Lemma 6.5 at last step, we get
 $$ \begin{align*} \sigma (x+y) + w &\leq x+y+w\leq \sigma (x)+\sigma (y)+w+2t\leq \sigma (x)+\sigma (y) + \sigma (x+y)\\ &\leq \sigma (x)+\sigma (y) + x + y = 2\sigma (x) + 2\sigma (y). \end{align*} $$
$$ \begin{align*} \sigma (x+y) + w &\leq x+y+w\leq \sigma (x)+\sigma (y)+w+2t\leq \sigma (x)+\sigma (y) + \sigma (x+y)\\ &\leq \sigma (x)+\sigma (y) + x + y = 2\sigma (x) + 2\sigma (y). \end{align*} $$
Passing to the supremum over all elements w way below
![]() $\sigma (x+y)$
, we obtain
$\sigma (x+y)$
, we obtain
Next, given
![]() $x,y \in S$
, using the above inequality together with the established superadditivity of
$x,y \in S$
, using the above inequality together with the established superadditivity of
![]() $\sigma $
, we get
$\sigma $
, we get
as desired.
Recall that a generalized
![]() $\mathrm {Cu}$
-morphism is a monoid morphism between
$\mathrm {Cu}$
-morphism is a monoid morphism between
![]() $\mathrm {Cu}$
-semigroups that preserves order and suprema of increasing sequences. We recall the definition of retract from [Reference Thiel and Vilalta42, Definition 3.14].
$\mathrm {Cu}$
-semigroups that preserves order and suprema of increasing sequences. We recall the definition of retract from [Reference Thiel and Vilalta42, Definition 3.14].
Definition 6.7. Let
![]() $S, T$
be
$S, T$
be
![]() $\mathrm {Cu}$
-semigroups. We say that S is a retract of T if there exist a
$\mathrm {Cu}$
-semigroups. We say that S is a retract of T if there exist a
![]() $\mathrm {Cu}$
-morphism
$\mathrm {Cu}$
-morphism
![]() $\iota \colon S\to T$
and a generalized
$\iota \colon S\to T$
and a generalized
![]() $\mathrm {Cu}$
-morphism
$\mathrm {Cu}$
-morphism
![]() $\sigma \colon T\to S$
such that
$\sigma \colon T\to S$
such that
![]() $\sigma \circ \iota = {\operatorname {id}}_S$
.
$\sigma \circ \iota = {\operatorname {id}}_S$
.
Proposition 6.8. Let S be a countably based, left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Additionally, assume one of the following:
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Additionally, assume one of the following:
-
(i) S is almost unperforated;
-
(ii) S is inf-semilattice ordered;
-
(iii)
 $S\otimes \{ 0,\infty \}$
is algebraic.
$S\otimes \{ 0,\infty \}$
is algebraic.
Then,
![]() $\sigma $
is a generalized
$\sigma $
is a generalized
![]() $\mathrm {Cu}$
-morphism and
$\mathrm {Cu}$
-morphism and
![]() $S_{\mathrm {{soft}}}$
is a retract of S.
$S_{\mathrm {{soft}}}$
is a retract of S.
Proof. By Theorem 6.6, we only need to check that
![]() $\sigma $
is subadditive.
$\sigma $
is subadditive.
(i): If S is almost unperforated, then it follows from Proposition 4.6 that
![]() $S_{\mathrm {{soft}}}$
is unperforated. Given any pair
$S_{\mathrm {{soft}}}$
is unperforated. Given any pair
![]() $x,y\in S$
, we know from Theorem 6.6 that
$x,y\in S$
, we know from Theorem 6.6 that
Since this equality is in
![]() $S_{\mathrm {{soft}}}$
, it follows that
$S_{\mathrm {{soft}}}$
, it follows that
![]() $\sigma (x+y)=\sigma (x) + \sigma (y)$
.
$\sigma (x+y)=\sigma (x) + \sigma (y)$
.
For (ii) and (iii), note that it is enough to prove that
![]() $\sigma (x+y)\leq x+\sigma (y)$
for all
$\sigma (x+y)\leq x+\sigma (y)$
for all
![]() $x,y \in S$
. Indeed, if this inequality holds, one can use it at the second and last steps to get
$x,y \in S$
. Indeed, if this inequality holds, one can use it at the second and last steps to get
as required.
Given
![]() $x,y \in S$
, we proceed to verify that
$x,y \in S$
, we proceed to verify that
![]() $\sigma (x+y)\leq x+\sigma (y)$
. Let
$\sigma (x+y)\leq x+\sigma (y)$
. Let
![]() $w\in S$
satisfy
$w\in S$
satisfy
![]() $w \ll \sigma (x+y)$
. Choose
$w \ll \sigma (x+y)$
. Choose
![]() $y'\in S$
such that
$y'\in S$
such that
Since
![]() $\sigma (x+y)$
is strongly soft, it follows from [Reference Thiel and Vilalta40, Proposition 4.13] that there exists
$\sigma (x+y)$
is strongly soft, it follows from [Reference Thiel and Vilalta40, Proposition 4.13] that there exists
![]() $r\in S_{\mathrm {{soft}}}$
such that
$r\in S_{\mathrm {{soft}}}$
such that
Applying Proposition 6.3 (2), one gets
Applying [Reference Thiel and Vilalta43, Proposition 4.7], we obtain
![]() $t',t\in S$
such that
$t',t\in S$
such that
Using that S is
![]() $(2,\omega )$
-divisible, it follows from [Reference Thiel and Vilalta40, Proposition 5.6] that we may assume both
$(2,\omega )$
-divisible, it follows from [Reference Thiel and Vilalta40, Proposition 5.6] that we may assume both
![]() $t'$
and t to be strongly soft. Thus, as in the proof of Lemma 5.2, we can apply (O5) to obtain an element b satisfying
$t'$
and t to be strongly soft. Thus, as in the proof of Lemma 5.2, we can apply (O5) to obtain an element b satisfying
which implies
with
![]() $t\ll r \leq \infty (x+y)=\infty (x+b)$
.
$t\ll r \leq \infty (x+y)=\infty (x+b)$
.
Thus, since both w and r are strongly soft, left-soft separativity (in the form of Lemma 4.5) implies that
![]() $w\leq x+b$
. Since S is countably based and satisfies (O7), the infimum
$w\leq x+b$
. Since S is countably based and satisfies (O7), the infimum
![]() $(b\wedge \infty t')$
exists. Note that
$(b\wedge \infty t')$
exists. Note that
![]() $(b\wedge \infty t') + t'$
is soft because
$(b\wedge \infty t') + t'$
is soft because
![]() $(b\wedge \infty t') \leq \infty t'$
; see [Reference Thiel and Vilalta40, Theorem 4.14]. Then
$(b\wedge \infty t') \leq \infty t'$
; see [Reference Thiel and Vilalta40, Theorem 4.14]. Then
and thus
![]() $b\wedge \infty t' \leq (b\wedge \infty t') + t' \leq \sigma (y)$
by Proposition 6.3 (1).
$b\wedge \infty t' \leq (b\wedge \infty t') + t' \leq \sigma (y)$
by Proposition 6.3 (1).
(ii): Assuming that S is inf-semilattice ordered, it now follows that
Passing to the supremum over all w way below
![]() $\sigma (x+y)$
, we get
$\sigma (x+y)$
, we get
![]() $\sigma (x+y)\leq x+\sigma (y)$
, as desired. This proves the case (ii).
$\sigma (x+y)\leq x+\sigma (y)$
, as desired. This proves the case (ii).
(iii): Let us additionally assume that
![]() $y\ll \infty y$
. Then, given w and r as before, we have that
$y\ll \infty y$
. Then, given w and r as before, we have that
![]() $y\ll \infty y\leq \infty r$
. This implies that there exists
$y\ll \infty y\leq \infty r$
. This implies that there exists
![]() $r'\in S$
such that
$r'\in S$
such that
![]() $r'\ll r$
and
$r'\ll r$
and
![]() $y\leq \infty r'$
. Using Proposition 6.3 at the last step, one gets
$y\leq \infty r'$
. Using Proposition 6.3 at the last step, one gets
with
![]() $r'\ll r \leq \infty (x+y)=\infty (x+\sigma (y))$
.
$r'\ll r \leq \infty (x+y)=\infty (x+\sigma (y))$
.
Therefore, we can use Lemma 4.4 to deduce that
![]() $w\leq x+\sigma (y)$
. Since this holds for every w way below
$w\leq x+\sigma (y)$
. Since this holds for every w way below
![]() $\sigma (x+y)$
, it follows that
$\sigma (x+y)$
, it follows that
![]() $\sigma (x+y)\leq x+\sigma (y)$
whenever
$\sigma (x+y)\leq x+\sigma (y)$
whenever
![]() $y\ll \infty y$
.
$y\ll \infty y$
.
If
![]() $S\otimes \{ 0,\infty \}$
is algebraic, then by [Reference Thiel and Vilalta43, Lemma 4.16] every
$S\otimes \{ 0,\infty \}$
is algebraic, then by [Reference Thiel and Vilalta43, Lemma 4.16] every
![]() $y \in S$
is the supremum of an increasing sequence
$y \in S$
is the supremum of an increasing sequence
![]() $(y_n)_n$
of elements
$(y_n)_n$
of elements
![]() $y_n \in S$
such that
$y_n \in S$
such that
![]() $y_n \ll \infty y_n$
. Using the above for each
$y_n \ll \infty y_n$
. Using the above for each
![]() $y_n$
and using that
$y_n$
and using that
![]() $\sigma $
preserves suprema of increasing sequences, we get
$\sigma $
preserves suprema of increasing sequences, we get
as desired.
Theorem 6.9. Let A be a separable
![]() $\mathrm {C}^*$
-algebra with the global Glimm property. Additionally, assume one of the following holds:
$\mathrm {C}^*$
-algebra with the global Glimm property. Additionally, assume one of the following holds:
-
(i) A has strict comparison of positive elements;
-
(ii) A has stable rank one;
-
(iii) A has topological dimension zero, and
 $ {\mathrm {Cu}} (A)$
is left-soft separative.
$ {\mathrm {Cu}} (A)$
is left-soft separative.
Then,
![]() $ {\mathrm {Cu}} (A)_{\mathrm {{soft}}}$
is a retract of
$ {\mathrm {Cu}} (A)_{\mathrm {{soft}}}$
is a retract of
![]() $ {\mathrm {Cu}} (A)$
.
$ {\mathrm {Cu}} (A)$
.
Proof. The Cuntz semigroup
![]() $ {\mathrm {Cu}}(A)$
is countably based and satisfies (O5)–(O7). Since A has the global Glimm property, it follows from [Reference Thiel and Vilalta43, Theorem 3.6] that
$ {\mathrm {Cu}}(A)$
is countably based and satisfies (O5)–(O7). Since A has the global Glimm property, it follows from [Reference Thiel and Vilalta43, Theorem 3.6] that
![]() $ {\mathrm {Cu}} (A)$
is
$ {\mathrm {Cu}} (A)$
is
![]() $(2,\omega )$
-divisible. We check that the additional conditions of Proposition 6.8 are satisfied:
$(2,\omega )$
-divisible. We check that the additional conditions of Proposition 6.8 are satisfied:
(i): Assume that A has has strict comparison of positive elements. Then
![]() $ {\mathrm {Cu}}(A)$
is almost unperforated by [Reference Elliott, Robert and Santiago20, Proposition 6.2] and left-soft separative by Proposition 4.8. This verifies Proposition 6.8 (i).
$ {\mathrm {Cu}}(A)$
is almost unperforated by [Reference Elliott, Robert and Santiago20, Proposition 6.2] and left-soft separative by Proposition 4.8. This verifies Proposition 6.8 (i).
(ii): Assume that A has stable rank one. Then
![]() $ {\mathrm {Cu}}(A)$
is inf-semilattice ordered by [Reference Antoine, Perera, Robert and Thiel2, Theorem 3.8], and left-soft separative by Proposition 4.3. This verifies Proposition 6.8 (ii).
$ {\mathrm {Cu}}(A)$
is inf-semilattice ordered by [Reference Antoine, Perera, Robert and Thiel2, Theorem 3.8], and left-soft separative by Proposition 4.3. This verifies Proposition 6.8 (ii).
(iii): Assume that A has topological dimension zero, and
![]() $ {\mathrm {Cu}} (A)$
is left-soft separative. Then
$ {\mathrm {Cu}} (A)$
is left-soft separative. Then
![]() $ {\mathrm {Cu}} (A)\otimes \{ 0,\infty \}$
is algebraic by [Reference Thiel and Vilalta43, Proposition 4.18]. This verifies Proposition 6.8 (iii).
$ {\mathrm {Cu}} (A)\otimes \{ 0,\infty \}$
is algebraic by [Reference Thiel and Vilalta43, Proposition 4.18]. This verifies Proposition 6.8 (iii).
Question 6.10. Let S be a countably based, weakly cancellative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Is the map
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Is the map
![]() $\sigma \colon S\to S_{\mathrm {{soft}}}$
subadditive?
$\sigma \colon S\to S_{\mathrm {{soft}}}$
subadditive?
With view towards the proof of subadditivity in Theorem 6.6, we ask the following question.
Question 6.11. Let S be the Cuntz semigroup of a
![]() $\mathrm {C}^*$
-algebra. Let
$\mathrm {C}^*$
-algebra. Let
![]() $x,y,z,w\in S$
satisfy
$x,y,z,w\in S$
satisfy
We know that
![]() $z\wedge w$
exists. Does it follow that
$z\wedge w$
exists. Does it follow that
![]() $x\leq y+(z\wedge w)$
?
$x\leq y+(z\wedge w)$
?
Question 6.11 above has a positive answer if S satisfies the interval axiom, as defined in [Reference Thiel and Vilalta39, Definition 9.3].
7 Dimension of a Cuntz semigroup and its soft part
Let S be a countably based, left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and assume that
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and assume that
![]() $\sigma \colon S\to S_{\mathrm {{soft}}}$
is a generalized
$\sigma \colon S\to S_{\mathrm {{soft}}}$
is a generalized
![]() $\mathrm {Cu}$
-morphism. We show that the (covering) dimension of S and
$\mathrm {Cu}$
-morphism. We show that the (covering) dimension of S and
![]() $S_{\mathrm {{soft}}}$
, as defined in [Reference Thiel and Vilalta42, Definition 3.1], are closely related: We have
$S_{\mathrm {{soft}}}$
, as defined in [Reference Thiel and Vilalta42, Definition 3.1], are closely related: We have
![]() $\dim (S_{\mathrm {{soft}}})\leq \dim (S)\leq \dim (S_{\mathrm {{soft}}})+1$
; see Proposition 7.2.
$\dim (S_{\mathrm {{soft}}})\leq \dim (S)\leq \dim (S_{\mathrm {{soft}}})+1$
; see Proposition 7.2.
Using the technique developed in [Reference Thiel and Vilalta38, Section 5], we remove the assumption that the
![]() $\mathrm {Cu}$
-semigroup is countably based; see Theorem 7.3. The result applies, in particular, to the Cuntz semigroup of every
$\mathrm {Cu}$
-semigroup is countably based; see Theorem 7.3. The result applies, in particular, to the Cuntz semigroup of every
![]() $\mathrm {C}^*$
-algebra with the global Glimm property that has either strict comparison of positive elements, stable rank one or topological dimension zero; see Corollary 7.4.
$\mathrm {C}^*$
-algebra with the global Glimm property that has either strict comparison of positive elements, stable rank one or topological dimension zero; see Corollary 7.4.
We also study the dimension of the fixed-point algebra
![]() $A^\alpha $
for a finite group action
$A^\alpha $
for a finite group action
![]() $\alpha $
; see Theorem 7.9.
$\alpha $
; see Theorem 7.9.
7.1 (Dimension of
 $\mathrm {Cu}$
-semigroups).
$\mathrm {Cu}$
-semigroups).
Recall from [Reference Thiel and Vilalta42, Definition 3.1] that, given a
![]() $\mathrm {Cu}$
-semigroup S and
$\mathrm {Cu}$
-semigroup S and
![]() $n\in {\mathbb {N}}$
, we say that S has dimension n, in symbols
$n\in {\mathbb {N}}$
, we say that S has dimension n, in symbols
![]() $\dim (S)=n$
, if n is the least integer such that, for any
$\dim (S)=n$
, if n is the least integer such that, for any
![]() $r\in {\mathbb {N}}$
, any pair
$r\in {\mathbb {N}}$
, any pair
![]() $x',x \in S$
, and any tuple
$x',x \in S$
, and any tuple
![]() $y_1,\ldots ,y_r\in S$
with
$y_1,\ldots ,y_r\in S$
with
![]() $x'\ll x\ll y_1+\ldots +y_r$
, there exist elements
$x'\ll x\ll y_1+\ldots +y_r$
, there exist elements
![]() $z_{j,k}\in S$
with
$z_{j,k}\in S$
with
![]() $j=1,\ldots ,r$
and
$j=1,\ldots ,r$
and
![]() $k=0,\ldots ,n$
such that:
$k=0,\ldots ,n$
such that:
-
(i)
 $z_{j,k}\ll y_j$
for every j and k;
$z_{j,k}\ll y_j$
for every j and k; -
(ii)
 $x'\ll \sum _{j,k}z_{j,k}$
;
$x'\ll \sum _{j,k}z_{j,k}$
; -
(iii)
 $\sum _{j}z_{j,k}\ll x$
for each k.
$\sum _{j}z_{j,k}\ll x$
for each k.
If no such n exists, we say that S has dimension
![]() $\infty $
, in symbols
$\infty $
, in symbols
![]() $\dim (S)=\infty $
.
$\dim (S)=\infty $
.
The next result generalizes [Reference Thiel and Vilalta42, Proposition 3.17] to the nonsimple setting.
Proposition 7.2. Let S be a countably based, left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and assume that
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and assume that
![]() $\sigma \colon S\to S_{\mathrm {{soft}}}$
is a generalized
$\sigma \colon S\to S_{\mathrm {{soft}}}$
is a generalized
![]() $\mathrm {Cu}$
-morphism. Then,
$\mathrm {Cu}$
-morphism. Then,
Proof. Since
![]() $\sigma $
is a generalized
$\sigma $
is a generalized
![]() $\mathrm {Cu}$
-morphism, the first inequality follows from [Reference Thiel and Vilalta42, Proposition 3.15]. To show the second inequality, set
$\mathrm {Cu}$
-morphism, the first inequality follows from [Reference Thiel and Vilalta42, Proposition 3.15]. To show the second inequality, set
![]() $n:=\dim (S_{\mathrm {{soft}}})$
, which we may assume to be finite. To verify that
$n:=\dim (S_{\mathrm {{soft}}})$
, which we may assume to be finite. To verify that
![]() $\dim (S)\leq n+1$
, let
$\dim (S)\leq n+1$
, let
![]() $x'\ll x\ll y_1+\ldots +y_r$
in S. We need to find
$x'\ll x\ll y_1+\ldots +y_r$
in S. We need to find
![]() $z_{j,k}\in S$
for
$z_{j,k}\in S$
for
![]() $j=1,\ldots ,r$
and
$j=1,\ldots ,r$
and
![]() $k=0,\ldots ,n+1$
such that
$k=0,\ldots ,n+1$
such that
-
(i)
 $z_{j,k}\ll y_j$
for each j and k;
$z_{j,k}\ll y_j$
for each j and k; -
(ii)
 $x'\ll \sum _{j,k}z_{j,k}$
;
$x'\ll \sum _{j,k}z_{j,k}$
; -
(iii)
 $\sum _j z_{j,k}\ll x$
for each k.
$\sum _j z_{j,k}\ll x$
for each k.
First, choose
![]() $x",x"'\in S$
such that
$x",x"'\in S$
such that
![]() $x'\ll x"\ll x"' \ll x$
. Applying that S satisfies (O6) for
$x'\ll x"\ll x"' \ll x$
. Applying that S satisfies (O6) for
![]() $x"\ll x"'\leq y_1+\ldots +y_r$
, we obtain
$x"\ll x"'\leq y_1+\ldots +y_r$
, we obtain
![]() $s_1,\ldots ,s_r\in S$
such that
$s_1,\ldots ,s_r\in S$
such that
Choose
![]() $s_1',\ldots ,s_r' \in S$
such that
$s_1',\ldots ,s_r' \in S$
such that
Using that S is
![]() $(2,\omega )$
-divisible (and consequently also
$(2,\omega )$
-divisible (and consequently also
![]() $(r,\omega )$
-divisible by [Reference Thiel and Vilalta43, Paragraph 2.4]), we obtain
$(r,\omega )$
-divisible by [Reference Thiel and Vilalta43, Paragraph 2.4]), we obtain
![]() $v\in S$
such that
$v\in S$
such that
For each j, we have
![]() $s_j \ll x"' \leq \infty v$
. Applying [Reference Thiel and Vilalta43, Proposition 4.10] to
$s_j \ll x"' \leq \infty v$
. Applying [Reference Thiel and Vilalta43, Proposition 4.10] to
we obtain
![]() $v_j\in S$
such that
$v_j\in S$
such that
Note that
Now, applying Proposition 6.3 at the second step, we have
Using that
![]() $S_{\mathrm {{soft}}}$
is a sub-
$S_{\mathrm {{soft}}}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup by Proposition 3.6, we can choose an element
$\mathrm {Cu}$
-semigroup by Proposition 3.6, we can choose an element
![]() $w\in S_{\mathrm {{soft}}}$
such that
$w\in S_{\mathrm {{soft}}}$
such that
Applying that
![]() $\dim (S_{\mathrm {{soft}}})\leq n$
for
$\dim (S_{\mathrm {{soft}}})\leq n$
for
![]() $w\ll \sigma (x")\leq \sigma (y_1)+\ldots +\sigma (y_r)$
, we obtain
$w\ll \sigma (x")\leq \sigma (y_1)+\ldots +\sigma (y_r)$
, we obtain
![]() $z_{j,k}\in S_{\mathrm {{soft}}}$
for
$z_{j,k}\in S_{\mathrm {{soft}}}$
for
![]() $j=1,\ldots ,r$
and
$j=1,\ldots ,r$
and
![]() $k=0,\ldots ,n$
such that
$k=0,\ldots ,n$
such that
-
(i’)
 $z_{j,k}\ll \sigma (y_j)$
for each j and
$z_{j,k}\ll \sigma (y_j)$
for each j and
 $k=0,\ldots ,n$
;
$k=0,\ldots ,n$
; -
(ii’)
 $w\ll \sum _{j}\sum _{k=0}^n z_{j,k}$
;
$w\ll \sum _{j}\sum _{k=0}^n z_{j,k}$
; -
(iii’)
 $\sum _j z_{j,k}\ll \sigma (x")$
for each
$\sum _j z_{j,k}\ll \sigma (x")$
for each
 $k=0,\ldots ,n$
.
$k=0,\ldots ,n$
.
Set
![]() $z_{j,n+1}:=v_j$
for each j. These elements satisfy conditions (i) and (iii). To verify (ii), we note that
$z_{j,n+1}:=v_j$
for each j. These elements satisfy conditions (i) and (iii). To verify (ii), we note that
 $$\begin{align*}x' \ll w+(v_1+\ldots+v_r) \ll (\sum_{j}\sum_{k=0}^n z_{j,k} )+(v_1+\ldots+v_r) = \sum_{j}\sum_{k=0}^{n+1} z_{j,k}, \end{align*}$$
$$\begin{align*}x' \ll w+(v_1+\ldots+v_r) \ll (\sum_{j}\sum_{k=0}^n z_{j,k} )+(v_1+\ldots+v_r) = \sum_{j}\sum_{k=0}^{n+1} z_{j,k}, \end{align*}$$
as desired.
Theorem 7.3. Let S be a left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Additionally, assume one of the following:
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Additionally, assume one of the following:
-
(i) S is almost unperforated;
-
(ii) S satisfies the Riesz interpolation property and the interval axiom;
-
(iii)
 $S\otimes \{ 0,\infty \}$
is algebraic.
$S\otimes \{ 0,\infty \}$
is algebraic.
Then,
![]() $\dim (S_{\mathrm {{soft}}})\leq \dim (S)\leq \dim (S_{\mathrm {{soft}}})+1$
.
$\dim (S_{\mathrm {{soft}}})\leq \dim (S)\leq \dim (S_{\mathrm {{soft}}})+1$
.
Proof. By [Reference Thiel and Vilalta38, Proposition 5.3], properties (O5), (O6) and (O7) each satisfy the Löwenheim–Skolem condition. Similarly, one can see that left-soft separativity,
![]() $(2,\omega )$
-divisibility, and the properties listed in (i)–(iii) each satisfy the Löwenheim–Skolem condition. (For (iii), one can use [Reference Thiel and Vilalta43, Lemma 4.16].) The proof is now analogous to [Reference Thiel and Vilalta38, Proposition 5.9] using Proposition 7.2.
$(2,\omega )$
-divisibility, and the properties listed in (i)–(iii) each satisfy the Löwenheim–Skolem condition. (For (iii), one can use [Reference Thiel and Vilalta43, Lemma 4.16].) The proof is now analogous to [Reference Thiel and Vilalta38, Proposition 5.9] using Proposition 7.2.
Corollary 7.4. Let A be a
![]() $\mathrm {C}^*$
-algebra with the global Glimm property. Additionally, assume one of the following:
$\mathrm {C}^*$
-algebra with the global Glimm property. Additionally, assume one of the following:
-
(i) A has strict comparison of positive elements;
-
(ii) A has stable rank one;
-
(iii) A has topological dimension zero, and
 $ {\mathrm {Cu}} (A)$
is left-soft separative.
$ {\mathrm {Cu}} (A)$
is left-soft separative.
Then,
![]() $\dim ( {\mathrm {Cu}} (A)_{\mathrm {{soft}}})\leq \dim ( {\mathrm {Cu}} (A))\leq \dim ( {\mathrm {Cu}} (A)_{\mathrm {{soft}}})+1$
.
$\dim ( {\mathrm {Cu}} (A)_{\mathrm {{soft}}})\leq \dim ( {\mathrm {Cu}} (A))\leq \dim ( {\mathrm {Cu}} (A)_{\mathrm {{soft}}})+1$
.
Proof. As in the proof of Theorem 6.9, we see that
![]() $ {\mathrm {Cu}}(A)$
satisfies the corresponding assumptions of Theorem 7.3, from which the result follows.
$ {\mathrm {Cu}}(A)$
satisfies the corresponding assumptions of Theorem 7.3, from which the result follows.
Notation 7.5. Let A be a
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $\alpha \colon G\to \mathrm {Aut}(A)$
be an action of a finite group G on A. We will denote by
$\alpha \colon G\to \mathrm {Aut}(A)$
be an action of a finite group G on A. We will denote by
![]() $C^* (G,A,\alpha )$
the induced crossed product.
$C^* (G,A,\alpha )$
the induced crossed product.
The fixed-point algebra
![]() $A^\alpha $
is defined as
$A^\alpha $
is defined as
7.6 (Fixed-point semigroups).
For a group action
![]() $\alpha $
on a
$\alpha $
on a
![]() $\mathrm {C}^*$
-algebra A, there are three natural objects that may be seen as the fixed-point semigroup of
$\mathrm {C}^*$
-algebra A, there are three natural objects that may be seen as the fixed-point semigroup of
![]() $ {\mathrm {Cu}} (A)$
: The Cuntz semigroup
$ {\mathrm {Cu}} (A)$
: The Cuntz semigroup
![]() $ {\mathrm {Cu}} (A^\alpha )$
, the fixed-point semigroup
$ {\mathrm {Cu}} (A^\alpha )$
, the fixed-point semigroup
![]() $ {\mathrm {Cu}} (A)^\alpha $
, and the fixed-point
$ {\mathrm {Cu}} (A)^\alpha $
, and the fixed-point
![]() $\mathrm {Cu}$
-semigroup
$\mathrm {Cu}$
-semigroup
![]() $ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
. We give some details.
$ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
. We give some details.
The fixed-point semigroup
![]() $ {\mathrm {Cu}} (A)^\alpha $
is defined as
$ {\mathrm {Cu}} (A)^\alpha $
is defined as
This is a submonoid of
![]() $ {\mathrm {Cu}}(A)$
that is closed under passing to suprema of increasing sequences. In general, it is not known if or when
$ {\mathrm {Cu}}(A)$
that is closed under passing to suprema of increasing sequences. In general, it is not known if or when
![]() $ {\mathrm {Cu}} (A)^\alpha $
is a sub-
$ {\mathrm {Cu}} (A)^\alpha $
is a sub-
![]() $\mathrm {Cu}$
-semigroup of
$\mathrm {Cu}$
-semigroup of
![]() $ {\mathrm {Cu}}(A)$
.
$ {\mathrm {Cu}}(A)$
.
An indexed collection
![]() $(x_t)_{t\in (0,1]}$
of elements in S is a path if
$(x_t)_{t\in (0,1]}$
of elements in S is a path if
![]() $x_t\ll x_r$
whenever
$x_t\ll x_r$
whenever
![]() $r<t$
and
$r<t$
and
![]() $x_t = \sup _{r<t}x_r$
for every
$x_t = \sup _{r<t}x_r$
for every
![]() $t\in (0,1]$
. The fixed-point
$t\in (0,1]$
. The fixed-point
![]() $\mathrm {Cu}$
-semigroup, as defined in [Reference Gardella and Santiago25, Definition 2.8], is
$\mathrm {Cu}$
-semigroup, as defined in [Reference Gardella and Santiago25, Definition 2.8], is
 $$\begin{align*}{\mathrm{Cu}} (A)^{{\mathrm{Cu}} (\alpha )} =\left\{ x\in{\mathrm{Cu}} (A) : \exists (x_t)_{t\in (0,1]}\text{ path in }{\mathrm{Cu}} (A) : \begin{array}{l} x_1=x,\text{ and }\\ {\mathrm{Cu}}(\alpha_g) (x_t) = x_t \,\,\forall t, g \end{array}\!\!\!\! \right\}. \end{align*}$$
$$\begin{align*}{\mathrm{Cu}} (A)^{{\mathrm{Cu}} (\alpha )} =\left\{ x\in{\mathrm{Cu}} (A) : \exists (x_t)_{t\in (0,1]}\text{ path in }{\mathrm{Cu}} (A) : \begin{array}{l} x_1=x,\text{ and }\\ {\mathrm{Cu}}(\alpha_g) (x_t) = x_t \,\,\forall t, g \end{array}\!\!\!\! \right\}. \end{align*}$$
Using [Reference Gardella and Santiago25, Lemma 2.9], one can show that
![]() $ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
is always a sub-
$ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
is always a sub-
![]() $\mathrm {Cu}$
-semigroup of
$\mathrm {Cu}$
-semigroup of
![]() $ {\mathrm {Cu}}(A)$
. Note that
$ {\mathrm {Cu}}(A)$
. Note that
![]() $ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
is contained in
$ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
is contained in
![]() $ {\mathrm {Cu}} (A)^{\alpha }$
. In Proposition 7.8, we will see a situation in which
$ {\mathrm {Cu}} (A)^{\alpha }$
. In Proposition 7.8, we will see a situation in which
![]() $ {\mathrm {Cu}}(A)^\alpha $
and
$ {\mathrm {Cu}}(A)^\alpha $
and
![]() $ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
agree.
$ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
agree.
Lemma 7.7. Let S be an inf-semilattice ordered
![]() $\mathrm {Cu}$
-semigroup, and let
$\mathrm {Cu}$
-semigroup, and let
![]() $\alpha $
be an action of a finite group G on S by
$\alpha $
be an action of a finite group G on S by
![]() $ {\mathrm {Cu}}$
-isomorphisms on S. Then the fixed-point semigroup
$ {\mathrm {Cu}}$
-isomorphisms on S. Then the fixed-point semigroup
![]() $S^\alpha := \{ x \in S : \alpha _g(x)=x \text { for all } g\in G \}$
is a sub-
$S^\alpha := \{ x \in S : \alpha _g(x)=x \text { for all } g\in G \}$
is a sub-
![]() $\mathrm {Cu}$
-semigroup of S.
$\mathrm {Cu}$
-semigroup of S.
Moreover, if S satisfies weak cancellation (resp. (O5), (O6), (O7)), then so does
![]() $S^\alpha $
.
$S^\alpha $
.
Proof. Define
![]() $\Phi \colon S \to S^\alpha $
by
$\Phi \colon S \to S^\alpha $
by
for
![]() $x \in S$
. For each
$x \in S$
. For each
![]() $x \in S$
, we have
$x \in S$
, we have
![]() $\Phi (\Phi (x)) = \Phi (x) \leq x$
; and we have
$\Phi (\Phi (x)) = \Phi (x) \leq x$
; and we have
![]() $\Phi (x)=x$
if and only if
$\Phi (x)=x$
if and only if
![]() $x \in S^\alpha $
.
$x \in S^\alpha $
.
It is straightforward to verify that
![]() $S^\alpha $
is a submonoid that is closed under suprema of increasing sequences. To show that
$S^\alpha $
is a submonoid that is closed under suprema of increasing sequences. To show that
![]() $S^\alpha $
is a sub-
$S^\alpha $
is a sub-
![]() $\mathrm {Cu}$
-semigroup, it remains to verify that for given
$\mathrm {Cu}$
-semigroup, it remains to verify that for given
![]() $x \in S^\alpha $
and
$x \in S^\alpha $
and
![]() $y \in S$
with
$y \in S$
with
![]() $y \ll x$
, there exists
$y \ll x$
, there exists
![]() $x' \in S^\alpha $
with
$x' \in S^\alpha $
with
![]() $y \leq x' \ll x$
.
$y \leq x' \ll x$
.
Let
![]() $(x_n)_n$
be a
$(x_n)_n$
be a
![]() $\ll $
-increasing sequence in S with supremum x. For each
$\ll $
-increasing sequence in S with supremum x. For each
![]() $g \in G$
, we have
$g \in G$
, we have
![]() $x = \alpha _g(x) = \sup _n \alpha _g(x_n)$
, and it follows that
$x = \alpha _g(x) = \sup _n \alpha _g(x_n)$
, and it follows that
Hence, there exists
![]() $n_0$
such that
$n_0$
such that
![]() $y \leq \Phi (x_{n_0})$
. Set
$y \leq \Phi (x_{n_0})$
. Set
![]() $x' := \Phi (x_{n_0})$
. Then
$x' := \Phi (x_{n_0})$
. Then
![]() $x' \in S^\alpha $
and
$x' \in S^\alpha $
and
which shows that
![]() $x'$
has the desired properties. Thus,
$x'$
has the desired properties. Thus,
![]() $S^\alpha $
is a sub-
$S^\alpha $
is a sub-
![]() $\mathrm {Cu}$
-semigroup.
$\mathrm {Cu}$
-semigroup.
Since
![]() $S^\alpha $
is a sub-
$S^\alpha $
is a sub-
![]() $\mathrm {Cu}$
-semigroup of S, it follows that
$\mathrm {Cu}$
-semigroup of S, it follows that
![]() $S^\alpha $
is weakly cancellative whenever S is. Assuming that S satisfies (O5), let us verify that so does
$S^\alpha $
is weakly cancellative whenever S is. Assuming that S satisfies (O5), let us verify that so does
![]() $S^\alpha $
. Let
$S^\alpha $
. Let
![]() $x',x,y',y,z \in S^\alpha $
satisfy
$x',x,y',y,z \in S^\alpha $
satisfy
Choose
![]() $y" \in S^\alpha $
satisfying
$y" \in S^\alpha $
satisfying
![]() $y' \ll y" \ll y$
. Applying (O5) in S, we obtain
$y' \ll y" \ll y$
. Applying (O5) in S, we obtain
![]() $c \in S$
such that
$c \in S$
such that
We claim that
![]() $\Phi (c)$
has the desired properties. Indeed, for each
$\Phi (c)$
has the desired properties. Indeed, for each
![]() $g \in G$
, we have
$g \in G$
, we have
Using that S is semilattice ordered, we get
We also have
Assuming that S satisfies (O6), let us verify that so does
![]() $S^\alpha $
. Let
$S^\alpha $
. Let
![]() $x',x,y,z \in S^\alpha $
satisfy
$x',x,y,z \in S^\alpha $
satisfy
It suffices to find
![]() $\tilde {e} \in S^\alpha $
such that
$\tilde {e} \in S^\alpha $
such that
(One can then apply this argument with the roles of y and z reversed to verify (O6).) Applying (O6) in S, we obtain
![]() $e \in S$
such that
$e \in S$
such that
For each
![]() $g \in G$
, we have
$g \in G$
, we have
Using that S is semilattice-ordered, we get
 $$\begin{align*}x' \leq \bigwedge_{g \in G} \big( \alpha_g(e) + z \big) = \left(\bigwedge_{g \in G} \alpha_g(c) \right) + z = \Phi(e) + z. \end{align*}$$
$$\begin{align*}x' \leq \bigwedge_{g \in G} \big( \alpha_g(e) + z \big) = \left(\bigwedge_{g \in G} \alpha_g(c) \right) + z = \Phi(e) + z. \end{align*}$$
Further, we have
which shows that
![]() $\tilde {e} := \Phi (e) \in S^\alpha $
has the desired properties.
$\tilde {e} := \Phi (e) \in S^\alpha $
has the desired properties.
Similarly, one shows that (O7) passes from S to
![]() $S^\alpha $
.
$S^\alpha $
.
We refer to [Reference Gardella, Hirshberg and Santiago23, Definition 2.2] for the definition of the weak tracial Rokhlin property. The first isomorphism in the statement below is well known, but we add it here for the convenience of the reader.
Proposition 7.8. Let A be a nonelementary, stably finite, simple, unital
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $\alpha $
be a finite group action on A that has the weak tracial Rokhlin property. Then we have
$\alpha $
be a finite group action on A that has the weak tracial Rokhlin property. Then we have
Restricting to the soft parts, we obtain:
If, moreover, A is separable and has stable rank one, then
![]() $ {\mathrm {Cu}} (A)^\alpha $
is a simple, countably based, weakly cancellative,
$ {\mathrm {Cu}} (A)^\alpha $
is a simple, countably based, weakly cancellative,
![]() $(2,\omega )$
-divisible sub-
$(2,\omega )$
-divisible sub-
![]() $\mathrm {Cu}$
-semigroup of
$\mathrm {Cu}$
-semigroup of
![]() $ {\mathrm {Cu}} (A)$
satisfying (O5)–(O7).
$ {\mathrm {Cu}} (A)$
satisfying (O5)–(O7).
Proof. For any action of a finite group on a unital
![]() $\mathrm {C}^*$
-algebra, the fixed-point algebra is
$\mathrm {C}^*$
-algebra, the fixed-point algebra is
![]() $\ast $
-isomorphic to a corner of the crossed product; see [Reference Asadi-Vasfi, Golestani and Phillips11, Lemma 4.3(4)]. By [Reference Hirshberg and Orovitz27, Corollary 5.4],
$\ast $
-isomorphic to a corner of the crossed product; see [Reference Asadi-Vasfi, Golestani and Phillips11, Lemma 4.3(4)]. By [Reference Hirshberg and Orovitz27, Corollary 5.4],
![]() $C^*(G, A, \alpha )$
is simple, which implies that
$C^*(G, A, \alpha )$
is simple, which implies that
![]() $C^*(G, A, \alpha )$
and
$C^*(G, A, \alpha )$
and
![]() $A^\alpha $
are Morita equivalent and therefore have isomorphic Cuntz semigroups.
$A^\alpha $
are Morita equivalent and therefore have isomorphic Cuntz semigroups.
As noted in Paragraph 7.6,
![]() $ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
is contained in
$ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
is contained in
![]() $ {\mathrm {Cu}}(A)^\alpha $
in general, and
$ {\mathrm {Cu}}(A)^\alpha $
in general, and
![]() $ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
is always a sub-
$ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
is always a sub-
![]() $\mathrm {Cu}$
-semigroup of
$\mathrm {Cu}$
-semigroup of
![]() $ {\mathrm {Cu}}(A)$
. Let
$ {\mathrm {Cu}}(A)$
. Let
![]() $\iota \colon A ^\alpha \to A$
denote the inclusion map, and note that
$\iota \colon A ^\alpha \to A$
denote the inclusion map, and note that
![]() $ {\mathrm {Cu}}(\iota )$
takes image in
$ {\mathrm {Cu}}(\iota )$
takes image in
![]() $ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}$
.
$ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}$
.
To show that
![]() $ {\mathrm {Cu}}(A)^\alpha $
is contained in
$ {\mathrm {Cu}}(A)^\alpha $
is contained in
![]() $ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
, let
$ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}} (\alpha )}$
, let
![]() $x \in {\mathrm {Cu}} (A)^\alpha $
. If x is compact in
$x \in {\mathrm {Cu}} (A)^\alpha $
. If x is compact in
![]() $ {\mathrm {Cu}}(A)$
, then we can use the constant path
$ {\mathrm {Cu}}(A)$
, then we can use the constant path
![]() $x_t = x$
to see that
$x_t = x$
to see that
![]() $x \in {\mathrm {Cu}} (A)^{ {\mathrm {Cu}}(\alpha )}$
. On the other hand, if x is soft, then we can apply [Reference Asadi-Vasfi, Golestani and Phillips11, Lemma 5.4] to obtain
$x \in {\mathrm {Cu}} (A)^{ {\mathrm {Cu}}(\alpha )}$
. On the other hand, if x is soft, then we can apply [Reference Asadi-Vasfi, Golestani and Phillips11, Lemma 5.4] to obtain
![]() $y \in {\mathrm {Cu}}(A^\alpha )_{\mathrm {{soft}}}$
such that
$y \in {\mathrm {Cu}}(A^\alpha )_{\mathrm {{soft}}}$
such that
![]() $x = {\mathrm {Cu}}(\iota )(y)$
. Since
$x = {\mathrm {Cu}}(\iota )(y)$
. Since
![]() $ {\mathrm {Cu}}(\iota )$
takes image in
$ {\mathrm {Cu}}(\iota )$
takes image in
![]() $ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}$
, we have
$ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}$
, we have
![]() $x \in {\mathrm {Cu}} (A)^{ {\mathrm {Cu}}(\alpha )}$
. Since A is simple and stably finite, every Cuntz class is either compact or soft, and we have
$x \in {\mathrm {Cu}} (A)^{ {\mathrm {Cu}}(\alpha )}$
. Since A is simple and stably finite, every Cuntz class is either compact or soft, and we have
![]() $ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )} = {\mathrm {Cu}}(A)^\alpha $
.
$ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )} = {\mathrm {Cu}}(A)^\alpha $
.
We have shown
We know from [Reference Asadi-Vasfi, Golestani and Phillips11, Theorem 5.5] that
![]() $ {\mathrm {Cu}}(\iota )$
induces an order-isomorphism between the soft part of
$ {\mathrm {Cu}}(\iota )$
induces an order-isomorphism between the soft part of
![]() $ {\mathrm {Cu}}(A^\alpha )$
and
$ {\mathrm {Cu}}(A^\alpha )$
and
![]() $ {\mathrm {Cu}}(A)^\alpha \cap {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
, the
$ {\mathrm {Cu}}(A)^\alpha \cap {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
, the
![]() $\alpha $
-invariant elements in
$\alpha $
-invariant elements in
![]() $ {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
. It is easy to see that
$ {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
. It is easy to see that
![]() $ {\mathrm {Cu}}(\iota )$
maps
$ {\mathrm {Cu}}(\iota )$
maps
![]() $ {\mathrm {Cu}}(A^\alpha)_{\mathrm {{soft}}}$
into
$ {\mathrm {Cu}}(A^\alpha)_{\mathrm {{soft}}}$
into
![]() $ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}_{\mathrm {{soft}}}$
and that
$ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}_{\mathrm {{soft}}}$
and that
![]() $ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}_{\mathrm {{soft}}}$
is contained in
$ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}_{\mathrm {{soft}}}$
is contained in
![]() $ {\mathrm {Cu}}(A)^\alpha \cap {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
. Together, we get
$ {\mathrm {Cu}}(A)^\alpha \cap {\mathrm {Cu}}(A)_{\mathrm {{soft}}}$
. Together, we get
Since
![]() $A^\alpha $
is a simple, nonelementary
$A^\alpha $
is a simple, nonelementary
![]() $\mathrm {C}^*$
-algebra,
$\mathrm {C}^*$
-algebra,
![]() $ {\mathrm {Cu}} (A^\alpha )$
is a simple,
$ {\mathrm {Cu}} (A^\alpha )$
is a simple,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). It follows from Proposition 3.6 that
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). It follows from Proposition 3.6 that
![]() $ {\mathrm {Cu}}(A^\alpha )_{\mathrm {{soft}}}$
is a
$ {\mathrm {Cu}}(A^\alpha )_{\mathrm {{soft}}}$
is a
![]() $\mathrm {Cu}$
-semigroup that also satisfies (O5)–(O7).
$\mathrm {Cu}$
-semigroup that also satisfies (O5)–(O7).
Finally, assume that A is also separable and has stable rank one. Then
![]() $ {\mathrm {Cu}}(A)$
is a
$ {\mathrm {Cu}}(A)$
is a
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Further,
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7). Further,
![]() $ {\mathrm {Cu}}(A)$
is weakly cancellative and inf-semilattice ordered by [Reference Rørdam and Winter35, Theorem 4.3] and [Reference Antoine, Perera, Robert and Thiel2, Theorem 3.8]. Hence,
$ {\mathrm {Cu}}(A)$
is weakly cancellative and inf-semilattice ordered by [Reference Rørdam and Winter35, Theorem 4.3] and [Reference Antoine, Perera, Robert and Thiel2, Theorem 3.8]. Hence,
![]() $ {\mathrm {Cu}}(A)^\alpha $
satisfies (O5)–(O7) by Lemma 7.7.
$ {\mathrm {Cu}}(A)^\alpha $
satisfies (O5)–(O7) by Lemma 7.7.
We have seen that
![]() $ {\mathrm {Cu}} (A)^\alpha $
is a sub-
$ {\mathrm {Cu}} (A)^\alpha $
is a sub-
![]() $\mathrm {Cu}$
-semigroup of
$\mathrm {Cu}$
-semigroup of
![]() $ {\mathrm {Cu}}(A)$
. Thus, since
$ {\mathrm {Cu}}(A)$
. Thus, since
![]() $ {\mathrm {Cu}} (A)$
is simple and weakly cancellative, so is
$ {\mathrm {Cu}} (A)$
is simple and weakly cancellative, so is
![]() $ {\mathrm {Cu}} (A)^\alpha $
. To verify
$ {\mathrm {Cu}} (A)^\alpha $
. To verify
![]() $(2,\omega )$
-divisibility, let
$(2,\omega )$
-divisibility, let
![]() $x \in {\mathrm {Cu}} (A)^\alpha $
. Since A is simple and nonelementary, we know from Paragraph 2.3 that
$x \in {\mathrm {Cu}} (A)^\alpha $
. Since A is simple and nonelementary, we know from Paragraph 2.3 that
![]() $ {\mathrm {Cu}}(A)$
is
$ {\mathrm {Cu}}(A)$
is
![]() $(2,\omega )$
-divisible. Hence, there exists
$(2,\omega )$
-divisible. Hence, there exists
![]() $y \in {\mathrm {Cu}} (A)$
such that
$y \in {\mathrm {Cu}} (A)$
such that
![]() $2y\leq x\leq \infty y$
. Using [Reference Asadi-Vasfi, Golestani and Phillips11, Lemma 5.2], we find a nonzero element
$2y\leq x\leq \infty y$
. Using [Reference Asadi-Vasfi, Golestani and Phillips11, Lemma 5.2], we find a nonzero element
![]() $z \in {\mathrm {Cu}}(A)^\alpha $
satisfying
$z \in {\mathrm {Cu}}(A)^\alpha $
satisfying
![]() $z\leq y$
. Then
$z\leq y$
. Then
![]() $2z \leq x \leq \infty z$
, a priori in
$2z \leq x \leq \infty z$
, a priori in
![]() $ {\mathrm {Cu}}(A)$
but then also in
$ {\mathrm {Cu}}(A)$
but then also in
![]() $ {\mathrm {Cu}}(A)^\alpha $
since the inclusion
$ {\mathrm {Cu}}(A)^\alpha $
since the inclusion
![]() $ {\mathrm {Cu}}(A)^\alpha \to {\mathrm {Cu}}(A)$
is an order-embedding.
$ {\mathrm {Cu}}(A)^\alpha \to {\mathrm {Cu}}(A)$
is an order-embedding.
Theorem 7.9. Let A be a nonelementary, separable, simple, unital
![]() $\mathrm {C}^*$
-algebra of stable rank one, and let
$\mathrm {C}^*$
-algebra of stable rank one, and let
![]() $\alpha $
be a finite group action on A that has the weak tracial Rokhlin property. Then
$\alpha $
be a finite group action on A that has the weak tracial Rokhlin property. Then
and
Proof. By Proposition 7.8, we have
which immediately proves (4).
It also follows from Proposition 7.8 that
![]() $ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}}(\alpha )}$
is a simple, weakly cancellative (hence left-soft separative),
$ {\mathrm {Cu}} (A)^{ {\mathrm {Cu}}(\alpha )}$
is a simple, weakly cancellative (hence left-soft separative),
![]() $(2,\omega )$
-divisible sub-
$(2,\omega )$
-divisible sub-
![]() $\mathrm {Cu}$
-semigroup of
$\mathrm {Cu}$
-semigroup of
![]() $ {\mathrm {Cu}} (A)$
satisfying (O5)–(O7). Since S is simple,
$ {\mathrm {Cu}} (A)$
satisfying (O5)–(O7). Since S is simple,
![]() $S\otimes \{0,\infty \}$
is algebraic. (In fact,
$S\otimes \{0,\infty \}$
is algebraic. (In fact,
![]() $S\otimes \{0,\infty \} \cong \{0,\infty \}$
.) Therefore, we can apply Theorem 7.3 (iii) to obtain
$S\otimes \{0,\infty \} \cong \{0,\infty \}$
.) Therefore, we can apply Theorem 7.3 (iii) to obtain
Further, since
![]() $A^{\alpha }$
is simple and stably finite, we know from [Reference Thiel and Vilalta42, Remark 3.18] that
$A^{\alpha }$
is simple and stably finite, we know from [Reference Thiel and Vilalta42, Remark 3.18] that
The result now follows since
![]() $ {\mathrm {Cu}} (A^{\alpha })_{\mathrm {{soft}}} \cong {\mathrm {Cu}} (A)^{ {\mathrm {Cu}}(\alpha )}_{\mathrm {{soft}}}$
; see Proposition 7.8.
$ {\mathrm {Cu}} (A^{\alpha })_{\mathrm {{soft}}} \cong {\mathrm {Cu}} (A)^{ {\mathrm {Cu}}(\alpha )}_{\mathrm {{soft}}}$
; see Proposition 7.8.
Example 7.10. Let
![]() $n \geq 2$
, and let G be
$n \geq 2$
, and let G be
![]() $S_n$
, the symmetric group on the set
$S_n$
, the symmetric group on the set
![]() $\{1,...,n\}$
. Let
$\{1,...,n\}$
. Let
![]() $A=\mathcal {Z}^{\otimes n}\cong \mathcal {Z}$
, and let
$A=\mathcal {Z}^{\otimes n}\cong \mathcal {Z}$
, and let
![]() $\alpha \colon G \to {\mathrm {Aut}} (A)$
be the permutation action given by
$\alpha \colon G \to {\mathrm {Aut}} (A)$
be the permutation action given by
It follows from [Reference Hirshberg and Orovitz27, Example 5.10] that
![]() $\alpha $
has the weak tracial Rokhlin property. Thus, using Theorem 7.9, one has
$\alpha $
has the weak tracial Rokhlin property. Thus, using Theorem 7.9, one has
The crossed product
![]() $ {\mathrm {Cu}} (C^*(G, A, \alpha ))$
is simple and
$ {\mathrm {Cu}} (C^*(G, A, \alpha ))$
is simple and
![]() $\mathcal {Z}$
-stable; see Corollaries 5.4 and 5.7 from [Reference Hirshberg and Orovitz27]. Therefore, it follows from [Reference Thiel and Vilalta42, Proposition 3.22] that
$\mathcal {Z}$
-stable; see Corollaries 5.4 and 5.7 from [Reference Hirshberg and Orovitz27]. Therefore, it follows from [Reference Thiel and Vilalta42, Proposition 3.22] that
and, moreover, we have
![]() $\dim ( {\mathrm {Cu}} (A)^{ {\mathrm {Cu}}(\alpha )})\leq 2$
by Theorem 7.9.
$\dim ( {\mathrm {Cu}} (A)^{ {\mathrm {Cu}}(\alpha )})\leq 2$
by Theorem 7.9.
8 Radius of comparison of a Cuntz semigroup and its soft part
In this section, we show that, under the assumptions of Section 5, the radius of comparison of a
![]() $\mathrm {Cu}$
-semigroup is equal to that of its soft part; see Theorem 8.5. We deduce that the radius of comparison of a
$\mathrm {Cu}$
-semigroup is equal to that of its soft part; see Theorem 8.5. We deduce that the radius of comparison of a
![]() $\mathrm {C}^*$
-algebra A is equal to that of the soft part of its Cuntz semigroup whenever A is unital and separable, satisfies the global Glimm property, and has either stable rank one or strict comparison of positive elements; see Theorem 8.6. This can be seen as a generalization of [Reference Phillips31, Theorem 6.14] to the setting of nonsimple
$\mathrm {C}^*$
-algebra A is equal to that of the soft part of its Cuntz semigroup whenever A is unital and separable, satisfies the global Glimm property, and has either stable rank one or strict comparison of positive elements; see Theorem 8.6. This can be seen as a generalization of [Reference Phillips31, Theorem 6.14] to the setting of nonsimple
![]() $\mathrm {C}^*$
-algebras; see Remark 8.8.
$\mathrm {C}^*$
-algebras; see Remark 8.8.
We also study in Example 8.9 the radius of comparison of certain crossed products.
Proposition 8.1. Let S be a countably based, left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
![]() $x\in S$
. Then
$x\in S$
. Then
![]() $\widehat {x}=\widehat {\sigma (x)}$
.
$\widehat {x}=\widehat {\sigma (x)}$
.
Proof. By Theorem 5.10, there exists
![]() $w \in S_{\mathrm {{soft}}}$
such that
$w \in S_{\mathrm {{soft}}}$
such that
![]() $w \leq x$
and
$w \leq x$
and
![]() $\widehat {x}=\widehat {w}$
. Since
$\widehat {x}=\widehat {w}$
. Since
![]() $\sigma (x)$
is the largest strongly soft element dominated by x (Proposition 6.3), we get
$\sigma (x)$
is the largest strongly soft element dominated by x (Proposition 6.3), we get
![]() $w \leq \sigma (x)$
, and so
$w \leq \sigma (x)$
, and so
as required.
With the homeomorphism from Theorem 5.14 at hand, we can now relate the radius of comparison of S and
![]() $S_{\mathrm {{soft}}}$
. Let us first recall the definition of the radius of the comparison of
$S_{\mathrm {{soft}}}$
. Let us first recall the definition of the radius of the comparison of
![]() $\mathrm {Cu}$
-semigroups from Section 3.3 of [Reference Blackadar, Robert, Tikuisis, Toms and Winter13].
$\mathrm {Cu}$
-semigroups from Section 3.3 of [Reference Blackadar, Robert, Tikuisis, Toms and Winter13].
Definition 8.2. Given a
![]() $\mathrm {Cu}$
-semigroup S, a full element
$\mathrm {Cu}$
-semigroup S, a full element
![]() $e \in S$
and
$e \in S$
and
![]() $r>0$
, one says that the pair
$r>0$
, one says that the pair
![]() $(S,e)$
satisfies condition (R1) for r if
$(S,e)$
satisfies condition (R1) for r if
![]() $x,y \in S$
satisfy
$x,y \in S$
satisfy
![]() $x \leq y$
whenever
$x \leq y$
whenever
for all
![]() $\lambda \in F(S)$
.
$\lambda \in F(S)$
.
The radius of comparison of
![]() $(S,e)$
, denoted by
$(S,e)$
, denoted by
![]() $ {\mathrm {rc}} (S, e)$
, is the infimum of the positive elements r such that
$ {\mathrm {rc}} (S, e)$
, is the infimum of the positive elements r such that
![]() $(S,e)$
satisfies (R1) for r.
$(S,e)$
satisfies (R1) for r.
Remark 8.3. In [Reference Blackadar, Robert, Tikuisis, Toms and Winter13, Definition 3.3.2], for a
![]() $\mathrm {C}^*$
-algebra A and a full element
$\mathrm {C}^*$
-algebra A and a full element
![]() $a \in (A \otimes \mathcal {K})_+$
, the notation
$a \in (A \otimes \mathcal {K})_+$
, the notation
![]() $r_{A, a}$
is used for
$r_{A, a}$
is used for
![]() $ {\mathrm {rc}} ( {\mathrm {Cu}} (A),[a])$
. Also, it was shown in [Reference Blackadar, Robert, Tikuisis, Toms and Winter13, Proposition 3.2.3] that for unital
$ {\mathrm {rc}} ( {\mathrm {Cu}} (A),[a])$
. Also, it was shown in [Reference Blackadar, Robert, Tikuisis, Toms and Winter13, Proposition 3.2.3] that for unital
![]() $\mathrm {C}^*$
-algebras all of whose quotients are stably finite, the radius of comparison
$\mathrm {C}^*$
-algebras all of whose quotients are stably finite, the radius of comparison
![]() $ {\mathrm {rc}} ( {\mathrm {Cu}} (A),[ 1_A])$
coincides with the original notion of radius of comparison
$ {\mathrm {rc}} ( {\mathrm {Cu}} (A),[ 1_A])$
coincides with the original notion of radius of comparison
![]() $ {\mathrm {rc}} (A)$
as introduced in [Reference Toms44, Definition 6.1].
$ {\mathrm {rc}} (A)$
as introduced in [Reference Toms44, Definition 6.1].
Proposition 8.4. Let
![]() $\varphi \colon S \to T$
be a generalized
$\varphi \colon S \to T$
be a generalized
![]() $\mathrm {Cu}$
-morphism between
$\mathrm {Cu}$
-morphism between
![]() $\mathrm {Cu}$
-semigroups that is also an order embedding, and let
$\mathrm {Cu}$
-semigroups that is also an order embedding, and let
![]() $e \in S$
be a full element such that
$e \in S$
be a full element such that
![]() $\varphi (e)$
is full in T. Then,
$\varphi (e)$
is full in T. Then,
![]() $ {\mathrm {rc}} (S, e) \leq {\mathrm {rc}} (T, \varphi (e))$
.
$ {\mathrm {rc}} (S, e) \leq {\mathrm {rc}} (T, \varphi (e))$
.
Proof. Take
![]() $r>0$
. We show that
$r>0$
. We show that
![]() $(S,e)$
satisfies condition (R1) for r whenever
$(S,e)$
satisfies condition (R1) for r whenever
![]() $(T, \varphi (e))$
does, which readily implies the claimed inequality.
$(T, \varphi (e))$
does, which readily implies the claimed inequality.
Thus, assume that
![]() $(T, \varphi (e))$
satisfies condition (R1) for r. In order to verify that
$(T, \varphi (e))$
satisfies condition (R1) for r. In order to verify that
![]() $(S, e)$
satisfies (R1) for r as well, let
$(S, e)$
satisfies (R1) for r as well, let
![]() $x,y \in S$
satisfy
$x,y \in S$
satisfy
for all
![]() $\lambda \in F(S)$
.
$\lambda \in F(S)$
.
Note that, for every
![]() $\rho \in F(T)$
, we have that
$\rho \in F(T)$
, we have that
![]() $\rho \circ \varphi \in F(S)$
. Thus, we get
$\rho \circ \varphi \in F(S)$
. Thus, we get
for every
![]() $\rho \in F(T)$
. It follows from our assumption that
$\rho \in F(T)$
. It follows from our assumption that
![]() $\varphi (x) \leq \varphi (y)$
, and, since
$\varphi (x) \leq \varphi (y)$
, and, since
![]() $\varphi $
is an order-embedding, we deduce that
$\varphi $
is an order-embedding, we deduce that
![]() $x \leq y$
, as desired.
$x \leq y$
, as desired.
Theorem 8.5. Let S be a
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7), and let
![]() $e\in S$
be a full element. Then, there exists
$e\in S$
be a full element. Then, there exists
![]() $w \in S_{\mathrm {{soft}}}$
such that
$w \in S_{\mathrm {{soft}}}$
such that
If S is also countably based and left-soft separative, we have
Proof. By Theorem 5.10, we can pick
![]() $w \in S_{\mathrm {{soft}}}$
such that
$w \in S_{\mathrm {{soft}}}$
such that
Using at the first step that the inclusion map
![]() $\iota \colon S_{\mathrm {{soft}}} \to S$
is a
$\iota \colon S_{\mathrm {{soft}}} \to S$
is a
![]() $\mathrm {Cu}$
-morphism and an order-embedding and applying Proposition 8.4 and using at the last step that
$\mathrm {Cu}$
-morphism and an order-embedding and applying Proposition 8.4 and using at the last step that
![]() $\widehat {e}=\widehat {w}$
, we get
$\widehat {e}=\widehat {w}$
, we get
To prove the converse inequality, let
![]() $r>0$
and assume that
$r>0$
and assume that
![]() $(S_{\mathrm {{soft}}}, w)$
satisfies condition (R1) for r. Take
$(S_{\mathrm {{soft}}}, w)$
satisfies condition (R1) for r. Take
![]() $\varepsilon>0$
. We will show that
$\varepsilon>0$
. We will show that
![]() $(S,e)$
satisfies (R1) for
$(S,e)$
satisfies (R1) for
![]() $r+\varepsilon $
.
$r+\varepsilon $
.
Now, let
![]() $x,y\in S$
be such that
$x,y\in S$
be such that
![]() $\lambda (x)+(r+\varepsilon )\lambda (e)\leq \lambda (y)$
for every
$\lambda (x)+(r+\varepsilon )\lambda (e)\leq \lambda (y)$
for every
![]() $\lambda \in F(S)$
or, equivalently, such that
$\lambda \in F(S)$
or, equivalently, such that
in
![]() $ {\mathrm {LAff}} (F(S))$
.
$ {\mathrm {LAff}} (F(S))$
.
Applying [Reference Thiel and Vilalta40, Proposition 7.7], we find
![]() $k\in {\mathbb {N}}$
and then
$k\in {\mathbb {N}}$
and then
![]() $t \in S_{\mathrm {{soft}}}$
such that
$t \in S_{\mathrm {{soft}}}$
such that
Thus, we get
Note that, since e is full in S, so is t. By [Reference Thiel and Vilalta40, Theorem 4.14(2)], this implies that
![]() $x+t$
is strongly soft.
$x+t$
is strongly soft.
By Theorem 5.10, there exists
![]() $v\in S_{\mathrm {{soft}}}$
such that
$v\in S_{\mathrm {{soft}}}$
such that
![]() $v\leq y$
and
$v\leq y$
and
![]() $\widehat {v}=\widehat {y}$
. One gets
$\widehat {v}=\widehat {y}$
. One gets
or, equivalently, that
for every
![]() $\lambda \in F(S)$
.
$\lambda \in F(S)$
.
Using that
![]() $F(S)\cong F(S_{\mathrm {{soft}}})$
(Theorem 5.14) and that
$F(S)\cong F(S_{\mathrm {{soft}}})$
(Theorem 5.14) and that
![]() $(S_{\mathrm {{soft}}}, w)$
satisfies condition (R1) for r, it follows that
$(S_{\mathrm {{soft}}}, w)$
satisfies condition (R1) for r, it follows that
This shows that, given any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $(S,e)$
satisfies condition (R1) for
$(S,e)$
satisfies condition (R1) for
![]() $r+\varepsilon $
whenever
$r+\varepsilon $
whenever
![]() $(S_{\mathrm {{soft}}},w)$
satisfies (R1) for r. Consequently, we have
$(S_{\mathrm {{soft}}},w)$
satisfies (R1) for r. Consequently, we have
![]() $ {\mathrm {rc}}(S,e) \leq {\mathrm {rc}}(S_{\mathrm {{soft}}}, w)$
, as required.
$ {\mathrm {rc}}(S,e) \leq {\mathrm {rc}}(S_{\mathrm {{soft}}}, w)$
, as required.
Finally, if S is also countably based and left-soft separative, then we can use
![]() $w:=\sigma (e)$
by Proposition 8.1.
$w:=\sigma (e)$
by Proposition 8.1.
Theorem 8.6. Let A be a unital, separable
![]() $\mathrm {C}^*$
-algebra with the global Glimm property. Assume that A has stable rank one. Then
$\mathrm {C}^*$
-algebra with the global Glimm property. Assume that A has stable rank one. Then
Proof. Proceeding as in the proof of Theorem 6.9, we see that the assumptions on A imply that
![]() $ {\mathrm {Cu}}(A)$
is a countably based, left-soft separative,
$ {\mathrm {Cu}}(A)$
is a countably based, left-soft separative,
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroup satisfying (O5)–(O7) and that
$\mathrm {Cu}$
-semigroup satisfying (O5)–(O7) and that
![]() $[1]$
is full. Hence, the result follows from Theorem 8.5.
$[1]$
is full. Hence, the result follows from Theorem 8.5.
Corollary 8.7. Let A be a unital, separable, nowhere scattered
![]() $\mathrm {C}^*$
-algebra of stable rank one. Then
$\mathrm {C}^*$
-algebra of stable rank one. Then
Proof. By [Reference Thiel and Vilalta43, Proposition 7.3], A has the global Glimm property; see also [Reference Antoine, Perera, Robert and Thiel2, Section 5]. Further, by [Reference Blackadar, Robert, Tikuisis, Toms and Winter13, Proposition 3.2.3], we have
![]() $ {\mathrm {rc}}(A) = {\mathrm {rc}} \big ( {\mathrm {Cu}}(A),[1] \big )$
, and so the result follows from Theorem 8.6.
$ {\mathrm {rc}}(A) = {\mathrm {rc}} \big ( {\mathrm {Cu}}(A),[1] \big )$
, and so the result follows from Theorem 8.6.
Remark 8.8. For a large subalgebra B of a simple, unital, stably finite, nonelementary
![]() $\mathrm {C}^*$
-algebra A, it is shown in [Reference Phillips31, Theorem 6.8] that
$\mathrm {C}^*$
-algebra A, it is shown in [Reference Phillips31, Theorem 6.8] that
![]() $ {\mathrm {Cu}}(A)_{\mathrm {{soft}}}\cong {\mathrm {Cu}} (B)_{\mathrm {{soft}}}$
; see also Paragraph 3.5. Thus, using Theorem 8.5 at the first and last steps, one gets
$ {\mathrm {Cu}}(A)_{\mathrm {{soft}}}\cong {\mathrm {Cu}} (B)_{\mathrm {{soft}}}$
; see also Paragraph 3.5. Thus, using Theorem 8.5 at the first and last steps, one gets
which recovers [Reference Phillips31, Theorem 6.14].
Note that in this case the existence of
![]() $\sigma $
is provided by [Reference Engbers22].
$\sigma $
is provided by [Reference Engbers22].
Example 8.9. Let A be a nonelementary, separable, simple, unital
![]() $\mathrm {C}^*$
-algebra of stable rank one, real rank zero and such that the order of projections over A is determined by traces, and let
$\mathrm {C}^*$
-algebra of stable rank one, real rank zero and such that the order of projections over A is determined by traces, and let
![]() $\alpha $
be a finite group action on A that has the tracial Rokhlin property. Then
$\alpha $
be a finite group action on A that has the tracial Rokhlin property. Then
Indeed, by [Reference Archey9], the crossed product
![]() $C^*(G, A, \alpha )$
has stable rank one and then so does the fixed point algebra
$C^*(G, A, \alpha )$
has stable rank one and then so does the fixed point algebra
![]() $A^\alpha $
by [Reference Asadi-Vasfi, Golestani and Phillips11, Lemma 4.3]. The question of when stable rank one passes to crossed products by a finite group action with the (weak) tracial Rokhlin property is discussed after Corollary 5.6 in [Reference Asadi-Vasfi, Golestani and Phillips11]. One can also see that
$A^\alpha $
by [Reference Asadi-Vasfi, Golestani and Phillips11, Lemma 4.3]. The question of when stable rank one passes to crossed products by a finite group action with the (weak) tracial Rokhlin property is discussed after Corollary 5.6 in [Reference Asadi-Vasfi, Golestani and Phillips11]. One can also see that
![]() $A^\alpha $
is nonelementary, separable, simple and unital. Therefore,
$A^\alpha $
is nonelementary, separable, simple and unital. Therefore,
![]() $ {\mathrm {Cu}}(A^\alpha )$
is a countably based, weakly cancellative (hence, left-soft separative),
$ {\mathrm {Cu}}(A^\alpha )$
is a countably based, weakly cancellative (hence, left-soft separative),
![]() $(2,\omega )$
-divisible
$(2,\omega )$
-divisible
![]() $\mathrm {Cu}$
-semigroups satisfying (O5)–(O7). By Proposition 7.8, the
$\mathrm {Cu}$
-semigroups satisfying (O5)–(O7). By Proposition 7.8, the
![]() $\mathrm {Cu}$
-semigroup
$\mathrm {Cu}$
-semigroup
![]() $ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}$
has the same properties. Further, the soft parts of
$ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}$
has the same properties. Further, the soft parts of
![]() $ {\mathrm {Cu}}(A^\alpha )$
and
$ {\mathrm {Cu}}(A^\alpha )$
and
![]() $ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}$
are isomorphic by Proposition 7.8.
$ {\mathrm {Cu}}(A)^{ {\mathrm {Cu}}(\alpha )}$
are isomorphic by Proposition 7.8.
This allows us to apply Theorem 8.5 at the first and last steps, and we get
 $$ \begin{align*} {\mathrm{rc}} \big( {\mathrm{Cu}}(A^\alpha) ,[1] \big) &= {\mathrm{rc}} \big( {\mathrm{Cu}}(A^\alpha)_{\mathrm{{soft}}} ,\sigma([1]) \big) \\ &= {\mathrm{rc}} \big( {\mathrm{Cu}}(A)^{{\mathrm{Cu}}(\alpha)}_{\mathrm{{soft}}},\sigma([1]) \big) = {\mathrm{rc}} \big( {\mathrm{Cu}}(A)^{{\mathrm{Cu}}(\alpha)} ,[1] \big). \end{align*} $$
$$ \begin{align*} {\mathrm{rc}} \big( {\mathrm{Cu}}(A^\alpha) ,[1] \big) &= {\mathrm{rc}} \big( {\mathrm{Cu}}(A^\alpha)_{\mathrm{{soft}}} ,\sigma([1]) \big) \\ &= {\mathrm{rc}} \big( {\mathrm{Cu}}(A)^{{\mathrm{Cu}}(\alpha)}_{\mathrm{{soft}}},\sigma([1]) \big) = {\mathrm{rc}} \big( {\mathrm{Cu}}(A)^{{\mathrm{Cu}}(\alpha)} ,[1] \big). \end{align*} $$
Other examples where our results might be applicable are those obtained in [Reference Asadi-Vasfi10].
Acknowledgements
Part of this research was conducted during the Cuntz Semigroup Workshop 2021 at WWU Münster and during the short research visit of the third author to the first author at the Institute of Mathematics of the Czech Academy of Sciences. They thank both of the institutions for their hospitality.
This work was completed while the authors were attending the Thematic Program on Operator Algebras and Applications at the Fields Institute for Research in Mathematical Sciences in August and September 2023, and they gratefully acknowledge the support and hospitality of the Fields Institute.
Competing interest
None.