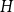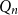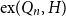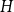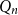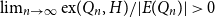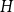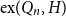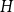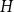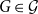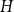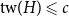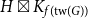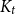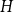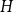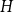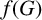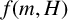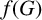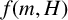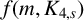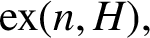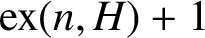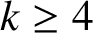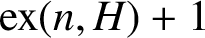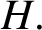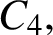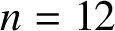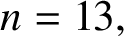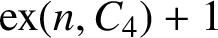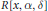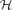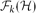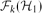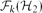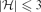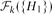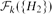Refine search
Actions for selected content:
19 results
Chi-Boundedness of graphs containing no cycles with k chords
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 November 2025, e189
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Glauber dynamics for the hard-core model on bounded-degree
 $H$-free graphs
$H$-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 19 September 2025, pp. 803-814
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting independent sets in structured graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 07 July 2025, pp. 625-634
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A SUFFICIENT CONDITION FOR PANCYCLIC GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 220-226
- Print publication:
- October 2025
-
- Article
- Export citation
BOREL LINE GRAPHS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A class of graphs of zero Turán density in a hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 404-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Product structure of graph classes with bounded treewidth
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 07 December 2023, pp. 351-376
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SIZE, SPECTRAL RADIUS, DISTANCE SPECTRAL RADIUS AND FRACTIONAL MATCHINGS IN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 187-199
- Print publication:
- October 2023
-
- Article
- Export citation
MAX-CUT BY EXCLUDING BIPARTITE SUBGRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 08 November 2022, pp. 177-186
- Print publication:
- October 2023
-
- Article
- Export citation
ON A PROBLEM OF ERDŐS ABOUT GRAPHS WHOSE SIZE IS THE TURÁN NUMBER PLUS ONE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 177-187
- Print publication:
- April 2022
-
- Article
- Export citation
On the structure of Dense graphs with bounded clique number
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 05 June 2020, pp. 641-649
-
- Article
- Export citation
Stability of the stochastic matching model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1064-1077
- Print publication:
- December 2016
-
- Article
- Export citation
Some Results on the Domination Number of a Zero-divisor Graph
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 573-578
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
GORENSTEIN AND Sr PATH IDEALS OF CYCLES
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 26 August 2014, pp. 7-15
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation
Forbidden Subgraphs Generating Almost the Same Sets
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 5 / September 2013
- Published online by Cambridge University Press:
- 11 July 2013, pp. 733-748
-
- Article
- Export citation
Cohen-Macaulay edge ideal whose height is half of the number of vertices
-
- Journal:
- Nagoya Mathematical Journal / Volume 201 / March 2011
- Published online by Cambridge University Press:
- 11 January 2016, pp. 117-131
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
TOPOLOGY OF INTERCONNECTION NETWORKS WITH GIVEN DEGREE AND DIAMETER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 350-352
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Non-Backtracking Random Walks and Cogrowth of Graphs
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 4 / 01 August 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 828-844
- Print publication:
- 01 August 2007
-
- Article
-
- You have access
- Export citation
Split Graphs with Specified Dilworth Numbers
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 1 / 01 March 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 43-47
- Print publication:
- 01 March 1984
-
- Article
-
- You have access
- Export citation