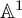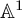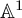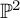Refine search
Actions for selected content:
2 results
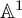 ${\mathbb A}^1$-CONNECTEDNESS OF MODULI OF VECTOR BUNDLES ON A CURVE
${\mathbb A}^1$-CONNECTEDNESS OF MODULI OF VECTOR BUNDLES ON A CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 1019-1027
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rationality problems and conjectures of Milnor and Bloch–Kato
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 1312-1326
- Print publication:
- August 2013
-
- Article
- Export citation