Article contents
Rationality problems and conjectures of Milnor and Bloch–Kato
Published online by Cambridge University Press: 03 June 2013
Abstract
We show how the techniques of Voevodsky’s proof of the Milnor conjecture and the Voevodsky–Rost proof of its generalization the Bloch–Kato conjecture can be used to study counterexamples to the classical Lüroth problem. By generalizing a method due to Peyre, we produce for any prime number  $\ell $ and any integer
$\ell $ and any integer  $n\geq 2$, a rationally connected, non-rational variety for which non-rationality is detected by a non-trivial degree
$n\geq 2$, a rationally connected, non-rational variety for which non-rationality is detected by a non-trivial degree  $n$ unramified étale cohomology class with
$n$ unramified étale cohomology class with 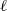 $\ell $-torsion coefficients. When
$\ell $-torsion coefficients. When 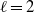 $\ell = 2$, the varieties that are constructed are furthermore unirational and non-rationality cannot be detected by a torsion unramified étale cohomology class of lower degree.
$\ell = 2$, the varieties that are constructed are furthermore unirational and non-rationality cannot be detected by a torsion unramified étale cohomology class of lower degree.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2013
References
- 8
- Cited by

