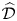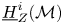Refine search
Actions for selected content:
1 results
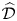 $\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations
$\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 28 October 2021, pp. 2553-2584
- Print publication:
- December 2021
-
- Article
- Export citation