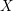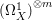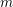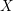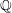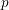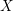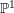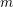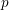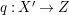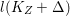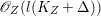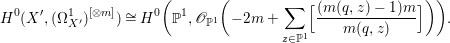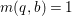1 Introduction
Recall that a complex projective variety ![]() $X$ is said to be rationally connected if for any two general points in
$X$ is said to be rationally connected if for any two general points in ![]() $X$, there exists a rational curve passing through them (see [Reference KollárKol96, Definition IV.3.2 and Proposition IV.3.6]). It is known that if
$X$, there exists a rational curve passing through them (see [Reference KollárKol96, Definition IV.3.2 and Proposition IV.3.6]). It is known that if ![]() $X$ is a smooth rationally connected variety, then
$X$ is a smooth rationally connected variety, then ![]() $X$ does not carry any non-zero pluri-form, that is
$X$ does not carry any non-zero pluri-form, that is 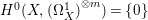 $H^{0}(X,({\rm\Omega}_{X}^{1})^{\otimes m})=\{0\}$ for
$H^{0}(X,({\rm\Omega}_{X}^{1})^{\otimes m})=\{0\}$ for ![]() $m>0$ (see [Reference KollárKol96, Corollary IV.3.8]). It is a conjecture that the converse is also true (see [Reference KollárKol96, Conjecture IV.3.8.1]). For singular varieties, there are also some analog results. The following theorems can be found in [Reference Greb, Kebekus and PeternellGKP14] and [Reference Greb, Kebekus, Kovács and PeternellGKKP11].
$m>0$ (see [Reference KollárKol96, Corollary IV.3.8]). It is a conjecture that the converse is also true (see [Reference KollárKol96, Conjecture IV.3.8.1]). For singular varieties, there are also some analog results. The following theorems can be found in [Reference Greb, Kebekus and PeternellGKP14] and [Reference Greb, Kebekus, Kovács and PeternellGKKP11].
Theorem 1.1. [Reference Greb, Kebekus and PeternellGKP14, Theorem 3.3]
If ![]() $X$ is a rationally connected variety with factorial canonical singularities, then
$X$ is a rationally connected variety with factorial canonical singularities, then 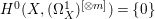 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})=\{0\}$ for
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})=\{0\}$ for ![]() $m>0$, where
$m>0$, where 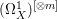 $({\rm\Omega}_{X}^{1})^{[\otimes m]}$ is the reflexive hull of
$({\rm\Omega}_{X}^{1})^{[\otimes m]}$ is the reflexive hull of 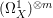 $({\rm\Omega}_{X}^{1})^{\otimes m}$.
$({\rm\Omega}_{X}^{1})^{\otimes m}$.
The reader is referred to Definition 2.6 for the notion of a klt pair.
Theorem 1.2. [Reference Greb, Kebekus, Kovács and PeternellGKKP11, Theorem 5.1]
If ![]() $(X,D)$ is a klt pair such that
$(X,D)$ is a klt pair such that ![]() $X$ is rationally connected, then
$X$ is rationally connected, then 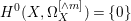 $H^{0}(X,{\rm\Omega}_{X}^{[\wedge m]})=\{0\}$ for
$H^{0}(X,{\rm\Omega}_{X}^{[\wedge m]})=\{0\}$ for ![]() $m>0$, where
$m>0$, where ![]() ${\rm\Omega}_{X}^{[\wedge m]}$ is the reflexive hull of
${\rm\Omega}_{X}^{[\wedge m]}$ is the reflexive hull of ![]() ${\rm\Omega}_{X}^{m}$.
${\rm\Omega}_{X}^{m}$.
Note that ![]() ${\rm\Omega}_{X}^{m}$ is a direct summand of
${\rm\Omega}_{X}^{m}$ is a direct summand of 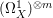 $({\rm\Omega}_{X}^{1})^{\otimes m}$, hence
$({\rm\Omega}_{X}^{1})^{\otimes m}$, hence 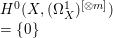 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})=\{0\}$ implies
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})=\{0\}$ implies 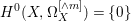 $H^{0}(X,{\rm\Omega}_{X}^{[\wedge m]})=\{0\}$. However, there are examples of klt rationally connected varieties whose canonical divisors are
$H^{0}(X,{\rm\Omega}_{X}^{[\wedge m]})=\{0\}$. However, there are examples of klt rationally connected varieties whose canonical divisors are ![]() $\mathbb{Q}$-effective (see [Reference TotaroTot12, Example 10] or [Reference KollárKol08, Example 43]). Moreover, Theorem 1.1 is not true if the variety is not factorial. A counterexample is given in [Reference Greb, Kebekus and PeternellGKP14, Example 3.7]. In [Reference OuOu14], we classify all rationally connected surfaces
$\mathbb{Q}$-effective (see [Reference TotaroTot12, Example 10] or [Reference KollárKol08, Example 43]). Moreover, Theorem 1.1 is not true if the variety is not factorial. A counterexample is given in [Reference Greb, Kebekus and PeternellGKP14, Example 3.7]. In [Reference OuOu14], we classify all rationally connected surfaces ![]() $X$ with canonical singularities such that
$X$ with canonical singularities such that 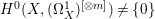 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some ![]() $m>0$. We obtain the following theorem.
$m>0$. We obtain the following theorem.
Theorem 1.3. [Reference OuOu14, Theorem 1.4]
Let ![]() $X$ be a rationally connected surface with canonical singularities. Then
$X$ be a rationally connected surface with canonical singularities. Then 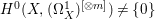 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some ![]() $m>0$ if and only if there is a fibration
$m>0$ if and only if there is a fibration 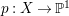 $p:X\rightarrow \mathbb{P}^{1}$ whose general fibers are isomorphic to
$p:X\rightarrow \mathbb{P}^{1}$ whose general fibers are isomorphic to ![]() $\mathbb{P}^{1}$ such that
$\mathbb{P}^{1}$ such that 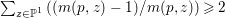 $\sum _{z\in \mathbb{P}^{1}}((m(p,z)-1)/m(p,z))\geqslant 2$, where
$\sum _{z\in \mathbb{P}^{1}}((m(p,z)-1)/m(p,z))\geqslant 2$, where ![]() $m(p,z)$ is the smallest positive coefficient in the divisor
$m(p,z)$ is the smallest positive coefficient in the divisor ![]() $p^{\ast }z$.
$p^{\ast }z$.
In this paper, we study the case of threefolds. We are interested in the structure of mildly singular rationally connected threefolds ![]() $X$ which carry non-zero pluri-forms, and we try to find out the source of these forms. If
$X$ which carry non-zero pluri-forms, and we try to find out the source of these forms. If 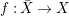 $f:\bar{X}\rightarrow X$ is the
$f:\bar{X}\rightarrow X$ is the ![]() $\mathbb{Q}$-factorial model, then
$\mathbb{Q}$-factorial model, then ![]() $f$ is an isomorphism in codimension
$f$ is an isomorphism in codimension ![]() $1$ and any pluri-forms of
$1$ and any pluri-forms of ![]() $X$ lift to
$X$ lift to ![]() $\bar{X}$. Hence, we can reduce to the case where the singularities of
$\bar{X}$. Hence, we can reduce to the case where the singularities of ![]() $X$ are
$X$ are ![]() $\mathbb{Q}$-factorial. If the threefold has terminal singularities, we prove the following result which is similar to Theorem 1.3.
$\mathbb{Q}$-factorial. If the threefold has terminal singularities, we prove the following result which is similar to Theorem 1.3.
Theorem 1.4. Let ![]() $X$ be a projective rationally connected threefold with
$X$ be a projective rationally connected threefold with ![]() $\mathbb{Q}$-factorial terminal singularities. Then
$\mathbb{Q}$-factorial terminal singularities. Then 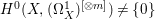 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some ![]() $m>0$ if and only if there is a fibration
$m>0$ if and only if there is a fibration 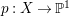 $p:X\rightarrow \mathbb{P}^{1}$ whose general fibers are smooth rationally connected surfaces such that
$p:X\rightarrow \mathbb{P}^{1}$ whose general fibers are smooth rationally connected surfaces such that 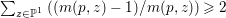 $\sum _{z\in \mathbb{P}^{1}}((m(p,z)-1)/m(p,z))\geqslant 2$, where
$\sum _{z\in \mathbb{P}^{1}}((m(p,z)-1)/m(p,z))\geqslant 2$, where ![]() $m(p,z)$ is the smallest positive coefficient in the divisor
$m(p,z)$ is the smallest positive coefficient in the divisor ![]() $p^{\ast }z$. Moreover, if this is the case, then for all
$p^{\ast }z$. Moreover, if this is the case, then for all ![]() $m>0$, we have
$m>0$, we have
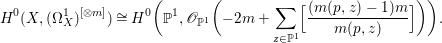 $$\begin{eqnarray}H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}\biggl(\mathbb{P}^{1},\mathscr{O}_{\mathbb{ P}^{1}}\biggl(-2m+\mathop{\sum }_{z\in \mathbb{P}^{1}}[\frac{(m(p,z)-1)m}{m(p,z)}]\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}\biggl(\mathbb{P}^{1},\mathscr{O}_{\mathbb{ P}^{1}}\biggl(-2m+\mathop{\sum }_{z\in \mathbb{P}^{1}}[\frac{(m(p,z)-1)m}{m(p,z)}]\biggr)\biggr).\end{eqnarray}$$ In particular, the number of ![]() $m$-pluri-forms depends only on the ramification of
$m$-pluri-forms depends only on the ramification of ![]() $p$.
$p$.
Construction 1.5. Thanks to Theorem 1.4, every rationally connected threefold ![]() $X$ with
$X$ with ![]() $\mathbb{Q}$-factorial terminal singularities such that
$\mathbb{Q}$-factorial terminal singularities such that 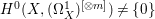 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some ![]() $m>0$ can be constructed as follows. There is a fibration
$m>0$ can be constructed as follows. There is a fibration 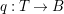 $q:T\rightarrow B$ from a normal threefold
$q:T\rightarrow B$ from a normal threefold ![]() $T$ to a smooth curve
$T$ to a smooth curve ![]() $B$ which has positive genus such that
$B$ which has positive genus such that 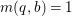 $m(q,b)=1$ for all
$m(q,b)=1$ for all ![]() $b\in B$. There is a finite group
$b\in B$. There is a finite group ![]() $G$ which acts on
$G$ which acts on ![]() $T$ and
$T$ and ![]() $B$ such that
$B$ such that ![]() $q$ is
$q$ is ![]() $G$-equivariant. By taking the quotient by
$G$-equivariant. By taking the quotient by ![]() $G$, we have
$G$, we have 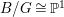 $B/G\cong \mathbb{P}^{1}$ and
$B/G\cong \mathbb{P}^{1}$ and 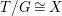 $T/G\cong X$. For more details, see Section 3.
$T/G\cong X$. For more details, see Section 3.
If the threefold ![]() $X$ has canonical singularities, we also obtain some necessary conditions for the existence of non-zero pluri-forms. As before, we reduce to the case where
$X$ has canonical singularities, we also obtain some necessary conditions for the existence of non-zero pluri-forms. As before, we reduce to the case where ![]() $X$ is
$X$ is ![]() $\mathbb{Q}$-factorial. We have the following theorem.
$\mathbb{Q}$-factorial. We have the following theorem.
Theorem 1.6. Let ![]() $X$ be a projective rationally connected threefold with
$X$ be a projective rationally connected threefold with ![]() $\mathbb{Q}$-factorial canonical singularities which carries non-zero pluri-forms. Let
$\mathbb{Q}$-factorial canonical singularities which carries non-zero pluri-forms. Let 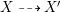 $X{\dashrightarrow}X^{\prime }$ be the result of a minimal model program. Then there is always an equidimensional fibration
$X{\dashrightarrow}X^{\prime }$ be the result of a minimal model program. Then there is always an equidimensional fibration 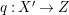 $q:X^{\prime }\rightarrow Z$ with
$q:X^{\prime }\rightarrow Z$ with 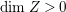 $\text{dim}\,Z>0$ such that
$\text{dim}\,Z>0$ such that 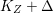 $K_{Z}+{\rm\Delta}$ is
$K_{Z}+{\rm\Delta}$ is ![]() $\mathbb{Q}$-effective. The divisor
$\mathbb{Q}$-effective. The divisor ![]() ${\rm\Delta}$ is defined by
${\rm\Delta}$ is defined by 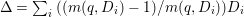 ${\rm\Delta}=\sum _{i}((m(q,D_{i})-1)/m(q,D_{i}))D_{i}$, where the
${\rm\Delta}=\sum _{i}((m(q,D_{i})-1)/m(q,D_{i}))D_{i}$, where the ![]() $D_{i}$ are all the prime divisors in
$D_{i}$ are all the prime divisors in ![]() $Z$ such that
$Z$ such that ![]() $q^{\ast }D_{i}$ is not reduced and
$q^{\ast }D_{i}$ is not reduced and 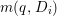 $m(q,D_{i})$ is the smallest positive coefficient in
$m(q,D_{i})$ is the smallest positive coefficient in ![]() $q^{\ast }D_{i}$. More precisely, we have the following two possibilities.
$q^{\ast }D_{i}$. More precisely, we have the following two possibilities.
(1) The variety
 $Z$ is a surface and
$Z$ is a surface and  $q:X^{\prime }\rightarrow Z$ is a Mori fibration such that there is a positive integer
$q:X^{\prime }\rightarrow Z$ is a Mori fibration such that there is a positive integer  $l$ such that
$l$ such that  $l(K_{Z}+{\rm\Delta})$ is an effective divisor. Moreover, the sections of
$l(K_{Z}+{\rm\Delta})$ is an effective divisor. Moreover, the sections of  $\mathscr{O}_{Z}(l(K_{Z}+{\rm\Delta}))$ lift to sections of
$\mathscr{O}_{Z}(l(K_{Z}+{\rm\Delta}))$ lift to sections of  ${\rm\Omega}_{X^{\prime }}^{[\otimes 2l]}$.
${\rm\Omega}_{X^{\prime }}^{[\otimes 2l]}$.(2) The variety
 $Z$ is isomorphic to
$Z$ is isomorphic to  $\mathbb{P}^{1}$ and for any
$\mathbb{P}^{1}$ and for any  $m>0$, we have
$m>0$, we have  $$\begin{eqnarray}H^{0}(X^{\prime },({\rm\Omega}_{X^{\prime }}^{1})^{[\otimes m]})\cong H^{0}\biggl(\mathbb{P}^{1},\mathscr{O}_{\mathbb{ P}^{1}}\biggl(-2m+\mathop{\sum }_{z\in \mathbb{P}^{1}}[\frac{(m(q,z)-1)m}{m(q,z)}]\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(X^{\prime },({\rm\Omega}_{X^{\prime }}^{1})^{[\otimes m]})\cong H^{0}\biggl(\mathbb{P}^{1},\mathscr{O}_{\mathbb{ P}^{1}}\biggl(-2m+\mathop{\sum }_{z\in \mathbb{P}^{1}}[\frac{(m(q,z)-1)m}{m(q,z)}]\biggr)\biggr).\end{eqnarray}$$
The difficulty in the case of canonical singularities is that the rational map 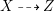 $X{\dashrightarrow}Z$ is not always regular. Moreover, even if it is, it may not be equidimensional. If klt singularities are permitted for our threefolds, then there exist other structures. We give an example of a rationally connected threefold of general type in Example 2.15.
$X{\dashrightarrow}Z$ is not always regular. Moreover, even if it is, it may not be equidimensional. If klt singularities are permitted for our threefolds, then there exist other structures. We give an example of a rationally connected threefold of general type in Example 2.15.
Outline of the paper. The main objective of this paper is to prove Theorem 1.4. We do this in several steps. First, we consider a projective rationally connected threefold ![]() $X$ with
$X$ with ![]() $\mathbb{Q}$-factorial canonical singularities which carries non-zero pluri-forms. Since it is rationally connected and has canonical singularities, its canonical divisor
$\mathbb{Q}$-factorial canonical singularities which carries non-zero pluri-forms. Since it is rationally connected and has canonical singularities, its canonical divisor ![]() $K_{X}$ is not pseudo-effective. Hence, if
$K_{X}$ is not pseudo-effective. Hence, if 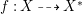 $f:X{\dashrightarrow}X^{\ast }$ is the result of a minimal model program for
$f:X{\dashrightarrow}X^{\ast }$ is the result of a minimal model program for ![]() $X$, then
$X$, then ![]() $K_{X^{\ast }}$ is not pseudo-effective either. Thus there is a Mori fibration
$K_{X^{\ast }}$ is not pseudo-effective either. Thus there is a Mori fibration 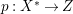 $p:X^{\ast }\rightarrow Z$ where
$p:X^{\ast }\rightarrow Z$ where ![]() $Z$ is a normal variety of dimension less than
$Z$ is a normal variety of dimension less than ![]() $3$. However, since
$3$. However, since ![]() $X$ carries non-zero pluri-forms, we have
$X$ carries non-zero pluri-forms, we have 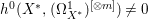 $h^{0}(X^{\ast },({\rm\Omega}_{X^{\ast }}^{1})^{[\otimes m]})\neq 0$ for some
$h^{0}(X^{\ast },({\rm\Omega}_{X^{\ast }}^{1})^{[\otimes m]})\neq 0$ for some ![]() $m>0$. This implies that
$m>0$. This implies that 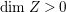 $\text{dim}\,Z>0$ by [Reference OuOu14, Theorem 3.1]. Hence, either
$\text{dim}\,Z>0$ by [Reference OuOu14, Theorem 3.1]. Hence, either 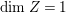 $\text{dim}\,Z=1$ or
$\text{dim}\,Z=1$ or 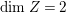 $\text{dim}\,Z=2$. We treat these two cases separately in Sections 3 and 4. If
$\text{dim}\,Z=2$. We treat these two cases separately in Sections 3 and 4. If 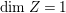 $\text{dim}\,Z=1$, then
$\text{dim}\,Z=1$, then ![]() $Z\cong \mathbb{P}^{1}$, and we show that
$Z\cong \mathbb{P}^{1}$, and we show that
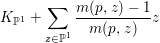 $$\begin{eqnarray}K_{\mathbb{P}^{1}}+\mathop{\sum }_{z\in \mathbb{P}^{1}}\frac{m(p,z)-1}{m(p,z)}z\end{eqnarray}$$
$$\begin{eqnarray}K_{\mathbb{P}^{1}}+\mathop{\sum }_{z\in \mathbb{P}^{1}}\frac{m(p,z)-1}{m(p,z)}z\end{eqnarray}$$ is ![]() $\mathbb{Q}$-effective, which is the same condition as in Theorem 1.4. If
$\mathbb{Q}$-effective, which is the same condition as in Theorem 1.4. If 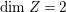 $\text{dim}\,Z=2$, then we define the
$\text{dim}\,Z=2$, then we define the ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() ${\rm\Delta}$ on
${\rm\Delta}$ on ![]() $Z$ as in Theorem 1.6. We prove that either
$Z$ as in Theorem 1.6. We prove that either 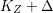 $K_{Z}+{\rm\Delta}$ is
$K_{Z}+{\rm\Delta}$ is ![]() $\mathbb{Q}$-effective or there is a fibration
$\mathbb{Q}$-effective or there is a fibration 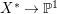 $X^{\ast }\rightarrow \mathbb{P}^{1}$ such that we can reduce to the situation of Section 3. In the last section, we assume that the variety
$X^{\ast }\rightarrow \mathbb{P}^{1}$ such that we can reduce to the situation of Section 3. In the last section, we assume that the variety ![]() $X$ has terminal singularities. In this case, there is always a fibration from
$X$ has terminal singularities. In this case, there is always a fibration from ![]() $X^{\ast }$ to
$X^{\ast }$ to ![]() $\mathbb{P}^{1}$ and we are always in the situation of Section 3. This fibration induces a dominant rational map from
$\mathbb{P}^{1}$ and we are always in the situation of Section 3. This fibration induces a dominant rational map from ![]() $X$ to
$X$ to ![]() $\mathbb{P}^{1}$. In the end, we prove that this rational map is regular and complete the proof of Theorem 1.4.
$\mathbb{P}^{1}$. In the end, we prove that this rational map is regular and complete the proof of Theorem 1.4.
2 Preliminaries
Throughout this paper, we work over ![]() $\mathbb{C}$, the field of complex numbers. Unless otherwise specified, every variety is an integral
$\mathbb{C}$, the field of complex numbers. Unless otherwise specified, every variety is an integral ![]() $\mathbb{C}$-scheme of finite type. A curve is a variety of dimension 1, a surface is a variety of dimension 2 and a threefold is a variety of dimension 3. A projective variety is called rationally chain connected if any two general points can be connected by a chain of rational curves. By [Reference Hacon and McKernanHM07, Corollary 1.8], a projective variety with klt singularities is rationally chain connected if and only if it is rationally connected. For a normal variety
$\mathbb{C}$-scheme of finite type. A curve is a variety of dimension 1, a surface is a variety of dimension 2 and a threefold is a variety of dimension 3. A projective variety is called rationally chain connected if any two general points can be connected by a chain of rational curves. By [Reference Hacon and McKernanHM07, Corollary 1.8], a projective variety with klt singularities is rationally chain connected if and only if it is rationally connected. For a normal variety ![]() $X$, let
$X$, let ![]() $K_{X}$ be a canonical divisor of
$K_{X}$ be a canonical divisor of ![]() $X$. We denote the sheaf of Kähler differentials by
$X$. We denote the sheaf of Kähler differentials by ![]() ${\rm\Omega}_{X}^{1}$ and let
${\rm\Omega}_{X}^{1}$ and let ![]() ${\rm\Omega}_{X}^{[1]}$ be its reflexive hull. Denote
${\rm\Omega}_{X}^{[1]}$ be its reflexive hull. Denote ![]() $\wedge ^{p}{\rm\Omega}_{X}^{1}$ by
$\wedge ^{p}{\rm\Omega}_{X}^{1}$ by ![]() ${\rm\Omega}_{X}^{p}$ for
${\rm\Omega}_{X}^{p}$ for ![]() $p\in \mathbb{N}$. Let
$p\in \mathbb{N}$. Let ![]() ${\rm\Omega}_{X}^{[\wedge p]}$ (resp.
${\rm\Omega}_{X}^{[\wedge p]}$ (resp. 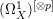 $({\rm\Omega}_{X}^{1})^{[\otimes p]}$) be the reflexive hull of
$({\rm\Omega}_{X}^{1})^{[\otimes p]}$) be the reflexive hull of ![]() ${\rm\Omega}_{X}^{p}$ (resp.
${\rm\Omega}_{X}^{p}$ (resp. ![]() $({\rm\Omega}_{X}^{1})^{\otimes p}$). We say that a normal variety
$({\rm\Omega}_{X}^{1})^{\otimes p}$). We say that a normal variety ![]() $X$ carries non-zero pluri-forms if
$X$ carries non-zero pluri-forms if 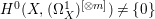 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some ![]() $m>0$. Let
$m>0$. Let 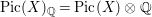 $\text{Pic}\,(X)_{\mathbb{Q}}=\,\text{Pic}\,(X)\otimes \mathbb{Q}$, where
$\text{Pic}\,(X)_{\mathbb{Q}}=\,\text{Pic}\,(X)\otimes \mathbb{Q}$, where ![]() $\,\text{Pic}\,(X)$ is the Picard group of
$\,\text{Pic}\,(X)$ is the Picard group of ![]() $X$. A
$X$. A ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() ${\rm\Delta}$ on
${\rm\Delta}$ on ![]() $X$ is called
$X$ is called ![]() $\mathbb{Q}$-effective if there is a positive integer
$\mathbb{Q}$-effective if there is a positive integer ![]() $k$ such that
$k$ such that ![]() $kD$ is a divisor and
$kD$ is a divisor and 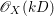 $\mathscr{O}_{X}(kD)$ has a non-zero global section.
$\mathscr{O}_{X}(kD)$ has a non-zero global section.
A fibration 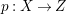 $p:X\rightarrow Z$ between normal quasi-projective varieties is a dominant proper morphism such that every fiber is connected, that is
$p:X\rightarrow Z$ between normal quasi-projective varieties is a dominant proper morphism such that every fiber is connected, that is 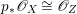 $p_{\ast }\mathscr{O}_{X}\cong \mathscr{O}_{Z}$. If
$p_{\ast }\mathscr{O}_{X}\cong \mathscr{O}_{Z}$. If ![]() $X\rightarrow Z$ is just a proper morphism, then we have the Stein factorization
$X\rightarrow Z$ is just a proper morphism, then we have the Stein factorization 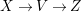 $X\rightarrow V\rightarrow Z$ such that
$X\rightarrow V\rightarrow Z$ such that ![]() $X\rightarrow V$ is a fibration and
$X\rightarrow V$ is a fibration and ![]() $V\rightarrow Z$ is finite (see [Reference HartshorneHar77, Corollary III. 11.5]). A Fano fibration is a fibration
$V\rightarrow Z$ is finite (see [Reference HartshorneHar77, Corollary III. 11.5]). A Fano fibration is a fibration ![]() $X\rightarrow Z$ such that
$X\rightarrow Z$ such that ![]() $-K_{X}$ is relatively ample. A Mori fibration is a Fano fibration such that the relative Picard number is
$-K_{X}$ is relatively ample. A Mori fibration is a Fano fibration such that the relative Picard number is ![]() $1$.
$1$.
Let 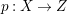 $p:X\rightarrow Z$ be a morphism and
$p:X\rightarrow Z$ be a morphism and ![]() $D$ be a prime
$D$ be a prime ![]() $\mathbb{Q}$-Cartier Weil divisor in
$\mathbb{Q}$-Cartier Weil divisor in ![]() $Z$. Let
$Z$. Let ![]() $k$ be a positive integer such that
$k$ be a positive integer such that ![]() $kD$ is Cartier. Denote the
$kD$ is Cartier. Denote the ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor 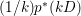 $(1/k)p^{\ast }(kD)$ by
$(1/k)p^{\ast }(kD)$ by ![]() $p^{\ast }D$. We define the multiplicity
$p^{\ast }D$. We define the multiplicity 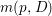 $m(p,D)$ by
$m(p,D)$ by
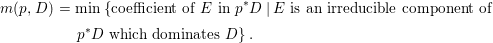 $$\begin{eqnarray}\displaystyle m(p,D) & = & \displaystyle \text{min}\left\{\text{coefficient of}~E~\text{in}~p^{\ast }D\mid E~\text{is an irreducible component of}\right.\nonumber\\ \displaystyle & & \displaystyle \left.p^{\ast }D~\text{which dominates}~D\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle m(p,D) & = & \displaystyle \text{min}\left\{\text{coefficient of}~E~\text{in}~p^{\ast }D\mid E~\text{is an irreducible component of}\right.\nonumber\\ \displaystyle & & \displaystyle \left.p^{\ast }D~\text{which dominates}~D\right\}.\nonumber\end{eqnarray}$$ By generic smoothness, there are only finitely many divisors ![]() $D$ such that
$D$ such that 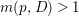 $m(p,D)>1$. Moreover, if
$m(p,D)>1$. Moreover, if 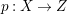 $p:X\rightarrow Z$ is a morphism from a normal variety to a smooth curve, then we define the ramification divisor
$p:X\rightarrow Z$ is a morphism from a normal variety to a smooth curve, then we define the ramification divisor ![]() $R$ as
$R$ as 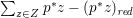 $\sum _{z\in Z}p^{\ast }z-(p^{\ast }z)_{\mathit{red}}$, where
$\sum _{z\in Z}p^{\ast }z-(p^{\ast }z)_{\mathit{red}}$, where ![]() $(p^{\ast }z)_{\mathit{red}}$ is the sum of the irreducible components of
$(p^{\ast }z)_{\mathit{red}}$ is the sum of the irreducible components of ![]() $p^{\ast }z$.
$p^{\ast }z$.
2.1 Reflexive sheaves on normal varieties
In this subsection, we gather some properties of reflexive sheaves. For a coherent sheaf ![]() $\mathscr{F}$ on a normal variety
$\mathscr{F}$ on a normal variety ![]() $X$, we denote by
$X$, we denote by ![]() $\mathscr{F}^{\ast \ast }$ the double dual of
$\mathscr{F}^{\ast \ast }$ the double dual of ![]() $\mathscr{F}$. The sheaf
$\mathscr{F}$. The sheaf ![]() $\mathscr{F}$ is reflexive if and only if
$\mathscr{F}$ is reflexive if and only if 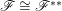 $\mathscr{F}\cong \mathscr{F}^{\ast \ast }$. In particular,
$\mathscr{F}\cong \mathscr{F}^{\ast \ast }$. In particular, ![]() $\mathscr{F}^{\ast \ast }$ is reflexive and we also call it the reflexive hull of
$\mathscr{F}^{\ast \ast }$ is reflexive and we also call it the reflexive hull of ![]() $\mathscr{F}$. Denote
$\mathscr{F}$. Denote 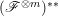 $(\mathscr{F}^{\otimes m})^{\ast \ast }$ by
$(\mathscr{F}^{\otimes m})^{\ast \ast }$ by ![]() $\mathscr{F}^{[\otimes m]}$ and
$\mathscr{F}^{[\otimes m]}$ and 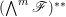 $(\wedge ^{m}\mathscr{F})^{\ast \ast }$ by
$(\wedge ^{m}\mathscr{F})^{\ast \ast }$ by ![]() $\mathscr{F}^{[\wedge m]}$ for any
$\mathscr{F}^{[\wedge m]}$ for any ![]() $m>0$. For two coherent sheaves
$m>0$. For two coherent sheaves ![]() $\mathscr{F}$ and
$\mathscr{F}$ and ![]() $\mathscr{G}$, let
$\mathscr{G}$, let 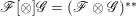 $\mathscr{F}[\otimes ]\mathscr{G}=(\mathscr{F}\otimes \mathscr{G})^{\ast \ast }$. The following proposition is an important criterion for reflexive sheaves on normal varieties.
$\mathscr{F}[\otimes ]\mathscr{G}=(\mathscr{F}\otimes \mathscr{G})^{\ast \ast }$. The following proposition is an important criterion for reflexive sheaves on normal varieties.
Proposition 2.1. [Reference HartshorneHar80, Proposition 1.6]
Let ![]() $\mathscr{F}$ be a coherent sheaf on a normal variety
$\mathscr{F}$ be a coherent sheaf on a normal variety ![]() $X$. Then
$X$. Then ![]() $\mathscr{F}$ is reflexive if and only if
$\mathscr{F}$ is reflexive if and only if ![]() $\mathscr{F}$ is torsion-free and for each open
$\mathscr{F}$ is torsion-free and for each open ![]() $U\subseteq X$ and each closed subset
$U\subseteq X$ and each closed subset ![]() $Y\subseteq U$ of codimension at least 2,
$Y\subseteq U$ of codimension at least 2, 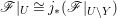 $\mathscr{F}|_{U}\cong j_{\ast }(\mathscr{F}|_{U\setminus Y})$, where
$\mathscr{F}|_{U}\cong j_{\ast }(\mathscr{F}|_{U\setminus Y})$, where 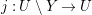 $j:U\setminus Y\rightarrow U$ is the inclusion map.
$j:U\setminus Y\rightarrow U$ is the inclusion map.
As a corollary of this proposition, we prove the following lemma.
Lemma 2.2. If 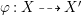 ${\it\varphi}:X{\dashrightarrow}X^{\prime }$ is a birational map between normal projective varieties such that
${\it\varphi}:X{\dashrightarrow}X^{\prime }$ is a birational map between normal projective varieties such that ![]() ${\it\varphi}^{-1}$ does not contract any divisor, then we have a natural injection
${\it\varphi}^{-1}$ does not contract any divisor, then we have a natural injection 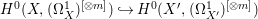 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]}){\hookrightarrow}H^{0}(X^{\prime },({\rm\Omega}_{X^{\prime }}^{1})^{[\otimes m]})$ for any integer
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]}){\hookrightarrow}H^{0}(X^{\prime },({\rm\Omega}_{X^{\prime }}^{1})^{[\otimes m]})$ for any integer ![]() $m>0$.
$m>0$.
Proof. Since the birational map 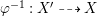 ${\it\varphi}^{-1}:X^{\prime }{\dashrightarrow}X$ does not contract any divisor, it induces an isomorphism from an open subset
${\it\varphi}^{-1}:X^{\prime }{\dashrightarrow}X$ does not contract any divisor, it induces an isomorphism from an open subset ![]() $W^{\prime }$ of
$W^{\prime }$ of ![]() $X^{\prime }$ such that
$X^{\prime }$ such that 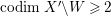 $\text{codim}\,X^{\prime }\setminus W\geqslant 2$ onto an open subset
$\text{codim}\,X^{\prime }\setminus W\geqslant 2$ onto an open subset ![]() $W$ of
$W$ of ![]() $X$. By Proposition 2.1, we have
$X$. By Proposition 2.1, we have 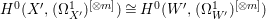 $H^{0}(X^{\prime },({\rm\Omega}_{X^{\prime }}^{1})^{[\otimes m]})\cong H^{0}(W^{\prime },({\rm\Omega}_{W^{\prime }}^{1})^{[\otimes m]})$ for any
$H^{0}(X^{\prime },({\rm\Omega}_{X^{\prime }}^{1})^{[\otimes m]})\cong H^{0}(W^{\prime },({\rm\Omega}_{W^{\prime }}^{1})^{[\otimes m]})$ for any ![]() $m>0$. Moreover, since
$m>0$. Moreover, since ![]() $W$ is an open subset of
$W$ is an open subset of ![]() $X$, we obtain
$X$, we obtain 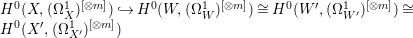 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]}){\hookrightarrow}H^{0}(W,({\rm\Omega}_{W}^{1})^{[\otimes m]})\cong H^{0}(W^{\prime },({\rm\Omega}_{W^{\prime }}^{1})^{[\otimes m]})\cong H^{0}(X^{\prime },({\rm\Omega}_{X^{\prime }}^{1})^{[\otimes m]})$ for all
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]}){\hookrightarrow}H^{0}(W,({\rm\Omega}_{W}^{1})^{[\otimes m]})\cong H^{0}(W^{\prime },({\rm\Omega}_{W^{\prime }}^{1})^{[\otimes m]})\cong H^{0}(X^{\prime },({\rm\Omega}_{X^{\prime }}^{1})^{[\otimes m]})$ for all ![]() $m>0$.◻
$m>0$.◻
The proof of the following lemma is left to the reader.
Lemma 2.3. Let 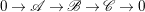 $0\rightarrow \mathscr{A}\rightarrow \mathscr{B}\rightarrow \mathscr{C}\rightarrow 0$ be an exact sequence of locally free sheaves on a variety
$0\rightarrow \mathscr{A}\rightarrow \mathscr{B}\rightarrow \mathscr{C}\rightarrow 0$ be an exact sequence of locally free sheaves on a variety ![]() $X$. Then, for any
$X$. Then, for any ![]() $m>0$, we have a filtration of locally free sheaves
$m>0$, we have a filtration of locally free sheaves 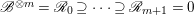 $\mathscr{B}^{\otimes m}=\mathscr{R}_{0}\supseteq \cdots \supseteq \mathscr{R}_{m+1}=0$ such that
$\mathscr{B}^{\otimes m}=\mathscr{R}_{0}\supseteq \cdots \supseteq \mathscr{R}_{m+1}=0$ such that 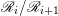 $\mathscr{R}_{i}/\mathscr{R}_{i+1}$ is isomorphic to the direct sum of copies of
$\mathscr{R}_{i}/\mathscr{R}_{i+1}$ is isomorphic to the direct sum of copies of 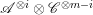 $\mathscr{A}^{\otimes i}\otimes \mathscr{C}^{\otimes m-i}$ for all
$\mathscr{A}^{\otimes i}\otimes \mathscr{C}^{\otimes m-i}$ for all 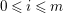 $0\leqslant i\leqslant m$.
$0\leqslant i\leqslant m$.
From this lemma, we can deduce the following lemma which is very important in the paper.
Lemma 2.4. Let 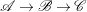 $\mathscr{A}\rightarrow \mathscr{B}\rightarrow \mathscr{C}$ be a complex of coherent sheaves on a normal variety
$\mathscr{A}\rightarrow \mathscr{B}\rightarrow \mathscr{C}$ be a complex of coherent sheaves on a normal variety ![]() $X$. Assume that there is an open subset
$X$. Assume that there is an open subset ![]() $W$ of
$W$ of ![]() $X$ with
$X$ with 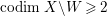 $\text{codim}\,X\setminus W\geqslant 2$ such that we have an exact sequence of locally free sheaves
$\text{codim}\,X\setminus W\geqslant 2$ such that we have an exact sequence of locally free sheaves 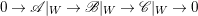 $0\rightarrow \mathscr{A}|_{W}\rightarrow \mathscr{B}|_{W}\rightarrow \mathscr{C}|_{W}\rightarrow 0$ on
$0\rightarrow \mathscr{A}|_{W}\rightarrow \mathscr{B}|_{W}\rightarrow \mathscr{C}|_{W}\rightarrow 0$ on ![]() $W$. If
$W$. If 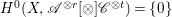 $H^{0}(X,\mathscr{A}^{\otimes r}[\otimes ]\mathscr{C}^{\otimes t})=\{0\}$ for all
$H^{0}(X,\mathscr{A}^{\otimes r}[\otimes ]\mathscr{C}^{\otimes t})=\{0\}$ for all ![]() $t>0$ and
$t>0$ and ![]() $r\geqslant 0$, then
$r\geqslant 0$, then 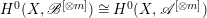 $H^{0}(X,\mathscr{B}^{[\otimes m]})\cong H^{0}(X,\mathscr{A}^{[\otimes m]})$ for all
$H^{0}(X,\mathscr{B}^{[\otimes m]})\cong H^{0}(X,\mathscr{A}^{[\otimes m]})$ for all ![]() $m>0$.
$m>0$.
Proof. On ![]() $W$, we have
$W$, we have 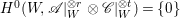 $H^{0}(W,\mathscr{A}|_{W}^{\otimes r}\otimes \mathscr{C}|_{W}^{\otimes t})=\{0\}$ for all
$H^{0}(W,\mathscr{A}|_{W}^{\otimes r}\otimes \mathscr{C}|_{W}^{\otimes t})=\{0\}$ for all ![]() $t>0$ and
$t>0$ and ![]() $r\geqslant 0$ by Proposition 2.1. If we fix
$r\geqslant 0$ by Proposition 2.1. If we fix ![]() $m>0$, by Lemma 2.3, we have a filtration
$m>0$, by Lemma 2.3, we have a filtration 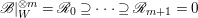 $\mathscr{B}|_{W}^{\otimes m}=\mathscr{R}_{0}\supseteq \cdots \supseteq \mathscr{R}_{m+1}=0$ such that
$\mathscr{B}|_{W}^{\otimes m}=\mathscr{R}_{0}\supseteq \cdots \supseteq \mathscr{R}_{m+1}=0$ such that 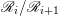 $\mathscr{R}_{i}/\mathscr{R}_{i+1}$ is isomorphic to the direct sum of copies of
$\mathscr{R}_{i}/\mathscr{R}_{i+1}$ is isomorphic to the direct sum of copies of 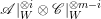 $\mathscr{A}|_{W}^{\otimes i}\otimes \mathscr{C}|_{W}^{\otimes m-i}$ for all
$\mathscr{A}|_{W}^{\otimes i}\otimes \mathscr{C}|_{W}^{\otimes m-i}$ for all 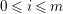 $0\leqslant i\leqslant m$. Since
$0\leqslant i\leqslant m$. Since 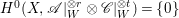 $H^{0}(X,\mathscr{A}|_{W}^{\otimes r}\otimes \mathscr{C}|_{W}^{\otimes t})=\{0\}$ for all
$H^{0}(X,\mathscr{A}|_{W}^{\otimes r}\otimes \mathscr{C}|_{W}^{\otimes t})=\{0\}$ for all ![]() $t>0$ and
$t>0$ and ![]() $r\geqslant 0$, we have
$r\geqslant 0$, we have 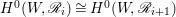 $H^{0}(W,\mathscr{R}_{i})\cong H^{0}(W,\mathscr{R}_{i+1})$ for
$H^{0}(W,\mathscr{R}_{i})\cong H^{0}(W,\mathscr{R}_{i+1})$ for 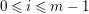 $0\leqslant i\leqslant m-1$. Thus
$0\leqslant i\leqslant m-1$. Thus 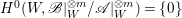 $H^{0}(W,\mathscr{B}|_{W}^{\otimes m}/\mathscr{A}|_{W}^{\otimes m})=\{0\}$ and
$H^{0}(W,\mathscr{B}|_{W}^{\otimes m}/\mathscr{A}|_{W}^{\otimes m})=\{0\}$ and 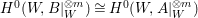 $H^{0}(W,B|_{W}^{\otimes m})\cong H^{0}(W,A|_{W}^{\otimes m})$. By Proposition 2.1, we have
$H^{0}(W,B|_{W}^{\otimes m})\cong H^{0}(W,A|_{W}^{\otimes m})$. By Proposition 2.1, we have 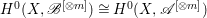 $H^{0}(X,\mathscr{B}^{[\otimes m]})\cong H^{0}(X,\mathscr{A}^{[\otimes m]})$.◻
$H^{0}(X,\mathscr{B}^{[\otimes m]})\cong H^{0}(X,\mathscr{A}^{[\otimes m]})$.◻
One of the applications of the lemma above is the following, which gives a relation between pluri-forms and fibrations.
Lemma 2.5. Let 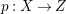 $p:X\rightarrow Z$ be a morphism between normal varieties. Assume that general fibers of
$p:X\rightarrow Z$ be a morphism between normal varieties. Assume that general fibers of ![]() $p$ do not carry any non-zero pluri-form. Then
$p$ do not carry any non-zero pluri-form. Then 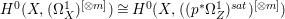 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]})$ for
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]})$ for ![]() $m>0$, where
$m>0$, where 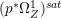 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ is the saturation of the image of
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ is the saturation of the image of ![]() $p^{\ast }{\rm\Omega}_{Z}^{1}$ in
$p^{\ast }{\rm\Omega}_{Z}^{1}$ in ![]() ${\rm\Omega}_{X}^{[1]}$.
${\rm\Omega}_{X}^{[1]}$.
Proof. We have an exact sequence of coherent sheaves 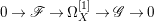 $0\rightarrow \mathscr{F}\rightarrow {\rm\Omega}_{X}^{[1]}\rightarrow \mathscr{G}\rightarrow 0$ on
$0\rightarrow \mathscr{F}\rightarrow {\rm\Omega}_{X}^{[1]}\rightarrow \mathscr{G}\rightarrow 0$ on ![]() $X$, where
$X$, where 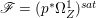 $\mathscr{F}=(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ and
$\mathscr{F}=(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ and ![]() $\mathscr{G}$ is a torsion-free sheaf. In particular,
$\mathscr{G}$ is a torsion-free sheaf. In particular, ![]() $\mathscr{G}$ is locally free in codimension
$\mathscr{G}$ is locally free in codimension ![]() $1$. Let
$1$. Let ![]() $V$ be the smooth locus of
$V$ be the smooth locus of ![]() $Z$ and let
$Z$ and let 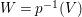 $W=p^{-1}(V)$. If
$W=p^{-1}(V)$. If ![]() $U$ is the largest open subset of
$U$ is the largest open subset of ![]() $W$ on which
$W$ on which ![]() $\mathscr{F}$,
$\mathscr{F}$, ![]() ${\rm\Omega}_{X}^{1}$ and
${\rm\Omega}_{X}^{1}$ and ![]() $\mathscr{G}$ are locally free, then
$\mathscr{G}$ are locally free, then 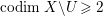 $\text{codim}\,X\setminus U\geqslant 2$ and we have an exact sequence
$\text{codim}\,X\setminus U\geqslant 2$ and we have an exact sequence 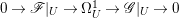 $0\rightarrow \mathscr{F}|_{U}\rightarrow {\rm\Omega}_{U}^{1}\rightarrow \mathscr{G}|_{U}\rightarrow 0$ of locally free sheaves on
$0\rightarrow \mathscr{F}|_{U}\rightarrow {\rm\Omega}_{U}^{1}\rightarrow \mathscr{G}|_{U}\rightarrow 0$ of locally free sheaves on ![]() $U$.
$U$.
If ![]() $F$ is a general fiber of
$F$ is a general fiber of ![]() $p|_{U}$, then
$p|_{U}$, then ![]() $\mathscr{F}|_{F}$ is the direct sum of
$\mathscr{F}|_{F}$ is the direct sum of ![]() $\mathscr{O}_{F}$ and
$\mathscr{O}_{F}$ and ![]() $\mathscr{G}|_{F}$ is isomorphic to
$\mathscr{G}|_{F}$ is isomorphic to ![]() ${\rm\Omega}_{F}^{1}$. Since general fibers of
${\rm\Omega}_{F}^{1}$. Since general fibers of ![]() $p$ do not carry any non-zero pluri-form, neither does
$p$ do not carry any non-zero pluri-form, neither does ![]() $F$ by Proposition 2.1. Hence, we have
$F$ by Proposition 2.1. Hence, we have 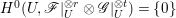 $H^{0}(U,\mathscr{F}|_{U}^{\otimes r}\otimes \mathscr{G}|_{U}^{\otimes t})=\{0\}$ for all
$H^{0}(U,\mathscr{F}|_{U}^{\otimes r}\otimes \mathscr{G}|_{U}^{\otimes t})=\{0\}$ for all ![]() $t>0$ and
$t>0$ and ![]() $r\geqslant 0$. By Lemma 2.4, we have an isomorphism from
$r\geqslant 0$. By Lemma 2.4, we have an isomorphism from 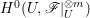 $H^{0}(U,\mathscr{F}|_{U}^{\otimes m})$ to
$H^{0}(U,\mathscr{F}|_{U}^{\otimes m})$ to 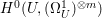 $H^{0}(U,({\rm\Omega}_{U}^{1})^{\otimes m})$ for all
$H^{0}(U,({\rm\Omega}_{U}^{1})^{\otimes m})$ for all ![]() $m>0$. By Proposition 2.1, we have
$m>0$. By Proposition 2.1, we have 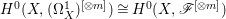 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,\mathscr{F}^{[\otimes m]})$ for all
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,\mathscr{F}^{[\otimes m]})$ for all ![]() $m>0$.◻
$m>0$.◻
If ![]() $X$ is a normal variety and
$X$ is a normal variety and ![]() $E$ is a Weil divisor on
$E$ is a Weil divisor on ![]() $X$, then
$X$, then ![]() $E$ is a Cartier divisor on the smooth locus
$E$ is a Cartier divisor on the smooth locus ![]() $U$ of
$U$ of ![]() $X$ and it induces an invertible sheaf
$X$ and it induces an invertible sheaf ![]() $\mathscr{O}_{U}(E)$ on
$\mathscr{O}_{U}(E)$ on ![]() $U$. Let
$U$. Let ![]() $\mathscr{O}_{X}(E)$ be the push-forward of
$\mathscr{O}_{X}(E)$ be the push-forward of ![]() $\mathscr{O}_{U}(E)$ on
$\mathscr{O}_{U}(E)$ on ![]() $X$. Then, by Proposition 2.1,
$X$. Then, by Proposition 2.1, ![]() $\mathscr{O}_{X}(E)$ is a reflexive sheaf on
$\mathscr{O}_{X}(E)$ is a reflexive sheaf on ![]() $X$ since
$X$ since ![]() $X$ is smooth in codimension
$X$ is smooth in codimension ![]() $1$. Conversely, if
$1$. Conversely, if ![]() $\mathscr{F}$ is a reflexive sheaf of rank
$\mathscr{F}$ is a reflexive sheaf of rank ![]() $1$ on
$1$ on ![]() $X$, it is an invertible sheaf in codimension
$X$, it is an invertible sheaf in codimension ![]() $1$. There is a Weil divisor
$1$. There is a Weil divisor ![]() $D$ on
$D$ on ![]() $X$ such that
$X$ such that 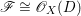 $\mathscr{F}\cong \mathscr{O}_{X}(D)$. If
$\mathscr{F}\cong \mathscr{O}_{X}(D)$. If ![]() $X$ is
$X$ is ![]() $\mathbb{Q}$-factorial, then for any
$\mathbb{Q}$-factorial, then for any ![]() $1$-cycle
$1$-cycle ![]() ${\it\alpha}$ on
${\it\alpha}$ on ![]() $X$, we can define the intersection number
$X$, we can define the intersection number 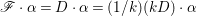 $\mathscr{F}\cdot {\it\alpha}=D\cdot {\it\alpha}=(1/k)(kD)\cdot {\it\alpha}$, where
$\mathscr{F}\cdot {\it\alpha}=D\cdot {\it\alpha}=(1/k)(kD)\cdot {\it\alpha}$, where ![]() $k$ is a positive integer such that
$k$ is a positive integer such that ![]() $kD$ is Cartier. This expression is independent of the choice of
$kD$ is Cartier. This expression is independent of the choice of ![]() $D$ (see [Reference ReidRei80, Appendix to Section 1] for more details).
$D$ (see [Reference ReidRei80, Appendix to Section 1] for more details).
2.2 Minimal model program
We recall some basic definitions and properties of the minimal model program (MMP). A pair ![]() $(X,{\rm\Delta})$ consists of a normal quasi-projective variety
$(X,{\rm\Delta})$ consists of a normal quasi-projective variety ![]() $X$ and a boundary
$X$ and a boundary ![]() ${\rm\Delta}$, that is a
${\rm\Delta}$, that is a ![]() $\mathbb{Q}$-Weil divisor
$\mathbb{Q}$-Weil divisor 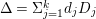 ${\rm\Delta}={\rm\Sigma}_{j=1}^{k}d_{j}D_{j}$ on
${\rm\Delta}={\rm\Sigma}_{j=1}^{k}d_{j}D_{j}$ on ![]() $X$ such that the
$X$ such that the ![]() $D_{j}$ are pairwise distinct prime divisors and all
$D_{j}$ are pairwise distinct prime divisors and all ![]() $d_{j}$ are contained in
$d_{j}$ are contained in ![]() $[0,1]$. Recall the definition of singularities of pairs.
$[0,1]$. Recall the definition of singularities of pairs.
Definition 2.6. [Reference Kollár and MoriKM98, Definition 2.34]
Let ![]() $(X,{\rm\Delta})$ be a pair with
$(X,{\rm\Delta})$ be a pair with 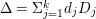 ${\rm\Delta}={\rm\Sigma}_{j=1}^{k}d_{j}D_{j}$. Let
${\rm\Delta}={\rm\Sigma}_{j=1}^{k}d_{j}D_{j}$. Let 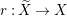 $r:\widetilde{X}\rightarrow X$ be a log resolution of singularities of
$r:\widetilde{X}\rightarrow X$ be a log resolution of singularities of ![]() $(X,{\rm\Delta})$. Assume that
$(X,{\rm\Delta})$. Assume that 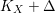 $K_{X}+{\rm\Delta}$ is
$K_{X}+{\rm\Delta}$ is ![]() $\mathbb{Q}$-Cartier, then we can write
$\mathbb{Q}$-Cartier, then we can write
 $$\begin{eqnarray}K_{\widetilde{X}}+r_{\ast }^{-1}{\rm\Delta}=r^{\ast }(K_{X}+{\rm\Delta})+{\rm\Sigma}a_{i}E_{i},\end{eqnarray}$$
$$\begin{eqnarray}K_{\widetilde{X}}+r_{\ast }^{-1}{\rm\Delta}=r^{\ast }(K_{X}+{\rm\Delta})+{\rm\Sigma}a_{i}E_{i},\end{eqnarray}$$ where the ![]() $E_{i}$ are
$E_{i}$ are ![]() $r$-exceptional divisors. We call
$r$-exceptional divisors. We call ![]() $a_{i}$ the discrepancy of
$a_{i}$ the discrepancy of ![]() $E_{i}$ with respect to
$E_{i}$ with respect to ![]() $(X,{\rm\Delta})$. Then
$(X,{\rm\Delta})$. Then ![]() $(X,{\rm\Delta})$ is terminal (resp. canonical, klt) if
$(X,{\rm\Delta})$ is terminal (resp. canonical, klt) if ![]() $a_{i}>0$ (resp.
$a_{i}>0$ (resp. ![]() $a_{i}\geqslant 0$,
$a_{i}\geqslant 0$, 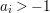 $a_{i}>-1$ and
$a_{i}>-1$ and ![]() $d_{j}<1$ for all
$d_{j}<1$ for all ![]() $j$) for all
$j$) for all ![]() $i$.
$i$.
Remark 2.7. If ![]() $X$ is terminal, then it is smooth in codimension
$X$ is terminal, then it is smooth in codimension ![]() $2$. If
$2$. If ![]() $X$ is canonical, then
$X$ is canonical, then ![]() $K_{X}$ is Cartier in codimension
$K_{X}$ is Cartier in codimension ![]() $2$ (see [Reference Kollár and MoriKM98, Corollary 5.18]).
$2$ (see [Reference Kollár and MoriKM98, Corollary 5.18]).
For a klt pair ![]() $(X,{\rm\Delta})$ such that
$(X,{\rm\Delta})$ such that ![]() $X$ is
$X$ is ![]() $\mathbb{Q}$-factorial, we can run a
$\mathbb{Q}$-factorial, we can run a 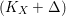 $(K_{X}+{\rm\Delta})$-MMP and obtain a sequence of rational maps
$(K_{X}+{\rm\Delta})$-MMP and obtain a sequence of rational maps 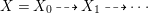 $X=X_{0}{\dashrightarrow}X_{1}{\dashrightarrow}\cdots \,$ such that
$X=X_{0}{\dashrightarrow}X_{1}{\dashrightarrow}\cdots \,$ such that 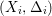 $(X_{i},{\rm\Delta}_{i})$ is a klt pair and
$(X_{i},{\rm\Delta}_{i})$ is a klt pair and ![]() $X_{i}$ is
$X_{i}$ is ![]() $\mathbb{Q}$-factorial, where
$\mathbb{Q}$-factorial, where ![]() ${\rm\Delta}_{i}$ is the strict transform of
${\rm\Delta}_{i}$ is the strict transform of ![]() ${\rm\Delta}$. Every elementary step in an MMP is either a divisorial contraction which is a morphism contracting an irreducible divisor or a flip which is an isomorphism in codimension
${\rm\Delta}$. Every elementary step in an MMP is either a divisorial contraction which is a morphism contracting an irreducible divisor or a flip which is an isomorphism in codimension ![]() $1$. More generally, if
$1$. More generally, if 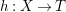 $h:X\rightarrow T$ is a morphism, we can run an
$h:X\rightarrow T$ is a morphism, we can run an ![]() $h$-relative MMP such that for all
$h$-relative MMP such that for all ![]() $i$, there is a morphism
$i$, there is a morphism 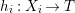 $h_{i}:X_{i}\rightarrow T$ with
$h_{i}:X_{i}\rightarrow T$ with 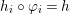 $h_{i}\circ {\it\varphi}_{i}=h$, where
$h_{i}\circ {\it\varphi}_{i}=h$, where ![]() ${\it\varphi}_{i}$ is the birational map
${\it\varphi}_{i}$ is the birational map 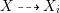 $X{\dashrightarrow}X_{i}$. For more details on the MMP, we refer to [Reference Kollár and MoriKM98, Section 3]. One of the most important problems in the MMP is that if the sequence of rational maps above terminates. If it does, we get the result of this
$X{\dashrightarrow}X_{i}$. For more details on the MMP, we refer to [Reference Kollár and MoriKM98, Section 3]. One of the most important problems in the MMP is that if the sequence of rational maps above terminates. If it does, we get the result of this ![]() $h$-relative MMP
$h$-relative MMP 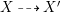 $X{\dashrightarrow}X^{\prime }$. Let
$X{\dashrightarrow}X^{\prime }$. Let ![]() ${\rm\Delta}^{\prime }$ be the direct image of
${\rm\Delta}^{\prime }$ be the direct image of ![]() ${\rm\Delta}$. Then either
${\rm\Delta}$. Then either 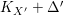 $K_{X^{\prime }}+{\rm\Delta}^{\prime }$ is relatively nef over
$K_{X^{\prime }}+{\rm\Delta}^{\prime }$ is relatively nef over ![]() $T$ (that is,
$T$ (that is, 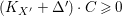 $(K_{X^{\prime }}+{\rm\Delta}^{\prime })\cdot C\geqslant 0$ for any curve
$(K_{X^{\prime }}+{\rm\Delta}^{\prime })\cdot C\geqslant 0$ for any curve ![]() $C$ in
$C$ in ![]() $X^{\prime }$ contracted by
$X^{\prime }$ contracted by 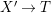 $X^{\prime }\rightarrow T$) or we have a
$X^{\prime }\rightarrow T$) or we have a 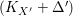 $(K_{X^{\prime }}+{\rm\Delta}^{\prime })$-Mori fibration
$(K_{X^{\prime }}+{\rm\Delta}^{\prime })$-Mori fibration 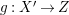 $g:X^{\prime }\rightarrow Z$ over
$g:X^{\prime }\rightarrow Z$ over ![]() $T$ such that
$T$ such that 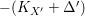 $-(K_{X^{\prime }}+{\rm\Delta}^{\prime })$ is
$-(K_{X^{\prime }}+{\rm\Delta}^{\prime })$ is ![]() $g$-ample. Thanks to [Reference KawamataKaw92, Theorem 1], we know that any MMP for a klt pair
$g$-ample. Thanks to [Reference KawamataKaw92, Theorem 1], we know that any MMP for a klt pair ![]() $(X,{\rm\Delta})$ such that
$(X,{\rm\Delta})$ such that 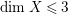 $\text{dim}\,X\leqslant 3$ terminates.
$\text{dim}\,X\leqslant 3$ terminates.
Lemma 2.8. Let 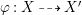 ${\it\varphi}:X{\dashrightarrow}X^{\prime }$ be an extremal divisorial contraction or a flip. Assume that
${\it\varphi}:X{\dashrightarrow}X^{\prime }$ be an extremal divisorial contraction or a flip. Assume that ![]() $X$ has
$X$ has ![]() $\mathbb{Q}$-factorial canonical singularities. If
$\mathbb{Q}$-factorial canonical singularities. If ![]() $Y$ is an irreducible closed subvariety in
$Y$ is an irreducible closed subvariety in ![]() $X^{\prime }$ such that it is the center of a divisor
$X^{\prime }$ such that it is the center of a divisor ![]() $E$ over
$E$ over ![]() $X^{\prime }$ which has discrepancy
$X^{\prime }$ which has discrepancy ![]() $0$, then
$0$, then ![]() ${\it\varphi}^{-1}$ is a morphism around the generic point of
${\it\varphi}^{-1}$ is a morphism around the generic point of ![]() $Y$.
$Y$.
Proof. Assume the opposite. Then the discrepancy of ![]() $E$ in
$E$ in ![]() $X$ is strictly smaller than the one in
$X$ is strictly smaller than the one in ![]() $X^{\prime }$ (see [Reference Kollár and MoriKM98, Lemma 3.38]). This implies that
$X^{\prime }$ (see [Reference Kollár and MoriKM98, Lemma 3.38]). This implies that ![]() $X$ does not have canonical singularities along the center of
$X$ does not have canonical singularities along the center of ![]() $E$ in
$E$ in ![]() $X$, which is a contradiction.◻
$X$, which is a contradiction.◻
Proposition 2.9. Let ![]() $X$ be a projective threefold which has canonical singularities. Let
$X$ be a projective threefold which has canonical singularities. Let ![]() $X^{\prime }$ be the result of an MMP for
$X^{\prime }$ be the result of an MMP for ![]() $X$ and denote the birational map
$X$ and denote the birational map 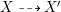 $X{\dashrightarrow}X^{\prime }$ by
$X{\dashrightarrow}X^{\prime }$ by ![]() $f$. Let
$f$. Let ![]() ${\rm\Gamma}$ be the normalization of the graph of
${\rm\Gamma}$ be the normalization of the graph of ![]() $f$. Then there is a natural isomorphism
$f$. Then there is a natural isomorphism 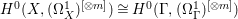 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})$ for all
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})$ for all ![]() $m>0$.
$m>0$.
Proof. Since there is a natural birational projection 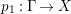 $p_{1}:{\rm\Gamma}\rightarrow X$, we have an injection from
$p_{1}:{\rm\Gamma}\rightarrow X$, we have an injection from 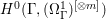 $H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})$ to
$H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})$ to 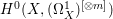 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ by Lemma 2.2. Let
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ by Lemma 2.2. Let 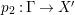 $p_{2}:{\rm\Gamma}\rightarrow X^{\prime }$ be the natural projection. Let
$p_{2}:{\rm\Gamma}\rightarrow X^{\prime }$ be the natural projection. Let 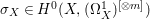 ${\it\sigma}_{X}\in H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ be a non-zero element. Since
${\it\sigma}_{X}\in H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ be a non-zero element. Since ![]() $X$,
$X$, ![]() ${\rm\Gamma}$ and
${\rm\Gamma}$ and ![]() $X^{\prime }$ are birational,
$X^{\prime }$ are birational, ![]() ${\it\sigma}_{X}$ induces a rational section
${\it\sigma}_{X}$ induces a rational section ![]() ${\it\sigma}_{{\rm\Gamma}}$ of
${\it\sigma}_{{\rm\Gamma}}$ of 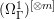 $({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]}$ and an element
$({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]}$ and an element ![]() ${\it\sigma}_{X^{\prime }}$ of
${\it\sigma}_{X^{\prime }}$ of 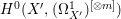 $H^{0}(X^{\prime },({\rm\Omega}_{X^{\prime }}^{1})^{[\otimes m]})$ (see Lemma 2.2). In order to prove that
$H^{0}(X^{\prime },({\rm\Omega}_{X^{\prime }}^{1})^{[\otimes m]})$ (see Lemma 2.2). In order to prove that ![]() ${\it\sigma}_{{\rm\Gamma}}$ is a regular section it is sufficient to prove that
${\it\sigma}_{{\rm\Gamma}}$ is a regular section it is sufficient to prove that ![]() ${\it\sigma}_{{\rm\Gamma}}$ does not have a pole along any
${\it\sigma}_{{\rm\Gamma}}$ does not have a pole along any ![]() $p_{1}$-exceptional divisor. Let
$p_{1}$-exceptional divisor. Let ![]() $E$ be an exceptional divisor for
$E$ be an exceptional divisor for ![]() $p_{1}$. Let
$p_{1}$. Let ![]() $C\subseteq E$ be a curve that is exceptional for
$C\subseteq E$ be a curve that is exceptional for ![]() $p_{1}$, then
$p_{1}$, then ![]() $C$ is not contracted by
$C$ is not contracted by ![]() $p_{2}$ since the graph of
$p_{2}$ since the graph of ![]() $f$ is included in
$f$ is included in 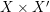 $X\times X^{\prime }$ and the normalization map is finite. Hence,
$X\times X^{\prime }$ and the normalization map is finite. Hence, 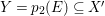 $Y=p_{2}(E)\subseteq X^{\prime }$ is a curve and
$Y=p_{2}(E)\subseteq X^{\prime }$ is a curve and ![]() $f^{-1}$ is not regular around the generic point of
$f^{-1}$ is not regular around the generic point of ![]() $Y$. By Lemma 2.8,
$Y$. By Lemma 2.8, ![]() $X^{\prime }$ has terminal singularities around the generic point of
$X^{\prime }$ has terminal singularities around the generic point of ![]() $Y$. Hence, it is smooth around the generic point of
$Y$. Hence, it is smooth around the generic point of ![]() $Y$ since
$Y$ since 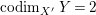 $\text{codim}_{X^{\prime }}\,Y=2$ (see [Reference Kollár and MoriKM98, Corollary 5.18]). Moreover, since
$\text{codim}_{X^{\prime }}\,Y=2$ (see [Reference Kollár and MoriKM98, Corollary 5.18]). Moreover, since ![]() $T$,
$T$, ![]() $X$ and
$X$ and ![]() $X^{\prime }$ are birational, the form
$X^{\prime }$ are birational, the form ![]() ${\it\sigma}_{{\rm\Gamma}}$ is just the pullback of
${\it\sigma}_{{\rm\Gamma}}$ is just the pullback of ![]() ${\it\sigma}_{X^{\prime }}$ by
${\it\sigma}_{X^{\prime }}$ by ![]() $p_{2}$. Hence,
$p_{2}$. Hence, ![]() ${\it\sigma}_{{\rm\Gamma}}$ does not have a pole along
${\it\sigma}_{{\rm\Gamma}}$ does not have a pole along ![]() $E$.◻
$E$.◻
2.3 Examples
We give some examples of rationally connected varieties which carry non-zero pluri-forms. First, we give an example of such varieties which have terminal singularities. For the construction of this example, we use the method of Theorem 3.2.
Example 2.10. Let 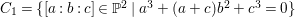 $C_{1}=\{[a:b:c]\in \mathbb{P}^{2}\mid a^{3}+(a+c)b^{2}+c^{3}=0\}$ be a smooth elliptic curve in
$C_{1}=\{[a:b:c]\in \mathbb{P}^{2}\mid a^{3}+(a+c)b^{2}+c^{3}=0\}$ be a smooth elliptic curve in ![]() $\mathbb{P}^{2}$. Let
$\mathbb{P}^{2}$. Let 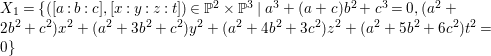 $X_{1}=\{([a:b:c],[x:y:z:t])\in \mathbb{P}^{2}\times \mathbb{P}^{3}\mid a^{3}+(a+c)b^{2}+c^{3}=0,(a^{2}+2b^{2}+c^{2})x^{2}+(a^{2}+3b^{2}+c^{2})y^{2}+(a^{2}+4b^{2}+3c^{2})z^{2}+(a^{2}+5b^{2}+6c^{2})t^{2}=0\}$. Then,
$X_{1}=\{([a:b:c],[x:y:z:t])\in \mathbb{P}^{2}\times \mathbb{P}^{3}\mid a^{3}+(a+c)b^{2}+c^{3}=0,(a^{2}+2b^{2}+c^{2})x^{2}+(a^{2}+3b^{2}+c^{2})y^{2}+(a^{2}+4b^{2}+3c^{2})z^{2}+(a^{2}+5b^{2}+6c^{2})t^{2}=0\}$. Then, ![]() $X_{1}$ is a smooth threefold and we have an induced fibration
$X_{1}$ is a smooth threefold and we have an induced fibration 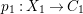 $p_{1}:X_{1}\rightarrow C_{1}$ such that all fibers of
$p_{1}:X_{1}\rightarrow C_{1}$ such that all fibers of ![]() $p_{1}$ are smooth quadric surfaces which are Fano surfaces. Moreover,
$p_{1}$ are smooth quadric surfaces which are Fano surfaces. Moreover, ![]() $X_{1}$ has Picard number
$X_{1}$ has Picard number ![]() $2$ by the Lefschetz theorem (see [Reference LazarsfeldLaz04, Example 3.1.23]). Hence,
$2$ by the Lefschetz theorem (see [Reference LazarsfeldLaz04, Example 3.1.23]). Hence, ![]() $p_{1}$ is a Mori fibration. Moreover, since
$p_{1}$ is a Mori fibration. Moreover, since ![]() $p_{1}$ is smooth, we have
$p_{1}$ is smooth, we have 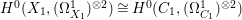 $H^{0}(X_{1},({\rm\Omega}_{X_{1}}^{1})^{\otimes 2})\cong H^{0}(C_{1},({\rm\Omega}_{C_{1}}^{1})^{\otimes 2})$ by Lemma 2.5. Let
$H^{0}(X_{1},({\rm\Omega}_{X_{1}}^{1})^{\otimes 2})\cong H^{0}(C_{1},({\rm\Omega}_{C_{1}}^{1})^{\otimes 2})$ by Lemma 2.5. Let ![]() $G$ be the group
$G$ be the group ![]() $\mathbb{Z}/2\mathbb{Z}$ and let
$\mathbb{Z}/2\mathbb{Z}$ and let ![]() $g\in G$ be the generator. We have an action of
$g\in G$ be the generator. We have an action of ![]() $G$ on
$G$ on 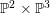 $\mathbb{P}^{2}\times \mathbb{P}^{3}$ defined by
$\mathbb{P}^{2}\times \mathbb{P}^{3}$ defined by 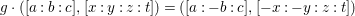 $g\cdot ([a:b:c],[x:y:z:t])=([a:-b:c],[-x:-y:z:t])$. This action induces an action of
$g\cdot ([a:b:c],[x:y:z:t])=([a:-b:c],[-x:-y:z:t])$. This action induces an action of ![]() $G$ on
$G$ on ![]() $X_{1}$ and an action of
$X_{1}$ and an action of ![]() $G$ on
$G$ on ![]() $C_{1}$ such that
$C_{1}$ such that ![]() $p_{1}$ in
$p_{1}$ in ![]() $G$-equivariant. We have
$G$-equivariant. We have 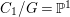 $C_{1}/G=\mathbb{P}^{1}$. The action of
$C_{1}/G=\mathbb{P}^{1}$. The action of ![]() $G$ on
$G$ on ![]() $X_{1}$ is free in codimension 2 and it has exactly 16 fixed points. Since
$X_{1}$ is free in codimension 2 and it has exactly 16 fixed points. Since 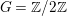 $G=\mathbb{Z}/2\mathbb{Z}$, the action of
$G=\mathbb{Z}/2\mathbb{Z}$, the action of ![]() $G$ on
$G$ on ![]() $X_{1}$ satisfies the condition of the first theorem in [Reference ReidRei87, Section 5]. Thus,
$X_{1}$ satisfies the condition of the first theorem in [Reference ReidRei87, Section 5]. Thus, 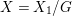 $X=X_{1}/G$ is a threefold which has
$X=X_{1}/G$ is a threefold which has ![]() $\mathbb{Q}$-factorial terminal singularities. We have a Fano fibration
$\mathbb{Q}$-factorial terminal singularities. We have a Fano fibration 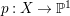 $p:X\rightarrow \mathbb{P}^{1}$ induced by
$p:X\rightarrow \mathbb{P}^{1}$ induced by ![]() $p_{1}$. Moreover, the Picard number of
$p_{1}$. Moreover, the Picard number of ![]() $X$ is not larger than the Picard number of
$X$ is not larger than the Picard number of ![]() $X_{1}$. Hence,
$X_{1}$. Hence, ![]() $p$ is a Mori fibration. Since general fibers of
$p$ is a Mori fibration. Since general fibers of ![]() $p$ are smooth quadric surfaces which are rationally connected,
$p$ are smooth quadric surfaces which are rationally connected, ![]() $X$ is rationally connected by [Reference Graber, Harris and StarrGHS03, Theorem 1.1]. In addition,
$X$ is rationally connected by [Reference Graber, Harris and StarrGHS03, Theorem 1.1]. In addition, 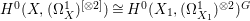 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes 2]})\cong H^{0}(X_{1},({\rm\Omega}_{X_{1}}^{1})^{\otimes 2})^{G}$ since
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes 2]})\cong H^{0}(X_{1},({\rm\Omega}_{X_{1}}^{1})^{\otimes 2})^{G}$ since 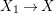 $X_{1}\rightarrow X$ is étale in codimension
$X_{1}\rightarrow X$ is étale in codimension ![]() $1$. Moreover,
$1$. Moreover, 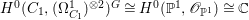 $H^{0}(C_{1},({\rm\Omega}_{C_{1}}^{1})^{\otimes 2})^{G}\cong H^{0}(\mathbb{P}^{1},\mathscr{O}_{\mathbb{P}^{1}})\cong \mathbb{C}$ (see [Reference OuOu14, Lemma 7.3]). Hence, we have
$H^{0}(C_{1},({\rm\Omega}_{C_{1}}^{1})^{\otimes 2})^{G}\cong H^{0}(\mathbb{P}^{1},\mathscr{O}_{\mathbb{P}^{1}})\cong \mathbb{C}$ (see [Reference OuOu14, Lemma 7.3]). Hence, we have 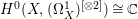 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes 2]})\cong \mathbb{C}$.
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes 2]})\cong \mathbb{C}$.
Remark 2.11. If ![]() $X$ is a normal rationally connected threefold and if
$X$ is a normal rationally connected threefold and if ![]() $X^{\ast }$ is the result of an MMP for
$X^{\ast }$ is the result of an MMP for ![]() $X$, then
$X$, then 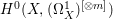 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ may be strictly included in
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ may be strictly included in 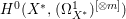 $H^{0}(X^{\ast },({\rm\Omega}_{X^{\ast }}^{1})^{[\otimes m]})$ for some
$H^{0}(X^{\ast },({\rm\Omega}_{X^{\ast }}^{1})^{[\otimes m]})$ for some ![]() $m>0$. For example, let
$m>0$. For example, let 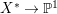 $X^{\ast }\rightarrow \mathbb{P}^{1}$ be the variety described in the example above. Then
$X^{\ast }\rightarrow \mathbb{P}^{1}$ be the variety described in the example above. Then ![]() $X^{\ast }$ carries non-zero pluri-forms. Let
$X^{\ast }$ carries non-zero pluri-forms. Let 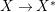 $X\rightarrow X^{\ast }$ be a resolution of singularities of
$X\rightarrow X^{\ast }$ be a resolution of singularities of ![]() $X^{\ast }$. Then
$X^{\ast }$. Then ![]() $X^{\ast }$ is the result of an MMP for
$X^{\ast }$ is the result of an MMP for ![]() $X$ since
$X$ since ![]() $X^{\ast }$ has terminal singularities. However, since
$X^{\ast }$ has terminal singularities. However, since ![]() $X$ is rationally connected and smooth, we have
$X$ is rationally connected and smooth, we have 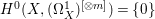 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})=\{0\}$ for any
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})=\{0\}$ for any ![]() $m>0$ (see [Reference KollárKol96, Corollary IV.3.8]).
$m>0$ (see [Reference KollárKol96, Corollary IV.3.8]).
We give two examples of rationally connected threefolds with canonical singularities which carry non-zero pluri-forms. In both cases, there is always a Mori fibration from the threefold ![]() $X$ to a surface
$X$ to a surface ![]() $Z$. In Example 2.12, the base
$Z$. In Example 2.12, the base ![]() $Z$ is a surface with klt singularities such that
$Z$ is a surface with klt singularities such that 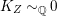 $K_{Z}{\sim}_{\mathbb{Q}}0$. In Example 2.14, the base
$K_{Z}{\sim}_{\mathbb{Q}}0$. In Example 2.14, the base ![]() $Z$ is isomorphic to
$Z$ is isomorphic to ![]() $\mathbb{P}^{2}$, which does not carry any non-zero pluri-forms.
$\mathbb{P}^{2}$, which does not carry any non-zero pluri-forms.
Example 2.12. Let ![]() $C$ be the curve in
$C$ be the curve in ![]() $\mathbb{P}^{2}$ defined by
$\mathbb{P}^{2}$ defined by 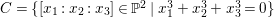 $C=\{[x_{1}:x_{2}:x_{3}]\in \mathbb{P}^{2}\mid x_{1}^{3}+x_{2}^{3}+x_{3}^{3}=0\}$. There exists an action of group
$C=\{[x_{1}:x_{2}:x_{3}]\in \mathbb{P}^{2}\mid x_{1}^{3}+x_{2}^{3}+x_{3}^{3}=0\}$. There exists an action of group 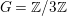 $G=\mathbb{Z}/3\mathbb{Z}$ on
$G=\mathbb{Z}/3\mathbb{Z}$ on ![]() $C$ defined by
$C$ defined by 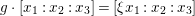 $g\cdot [x_{1}:x_{2}:x_{3}]=[{\it\xi}x_{1}:x_{2}:x_{3}]$, where
$g\cdot [x_{1}:x_{2}:x_{3}]=[{\it\xi}x_{1}:x_{2}:x_{3}]$, where ![]() $g$ is a generator of
$g$ is a generator of ![]() $G$ and
$G$ and ![]() ${\it\xi}$ is a primitive third root of unity. Let
${\it\xi}$ is a primitive third root of unity. Let 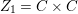 $Z_{1}=C\times C$. Then there is an induced action of
$Z_{1}=C\times C$. Then there is an induced action of ![]() $G$ on
$G$ on ![]() $Z_{1}$ which acts diagonally. We have that
$Z_{1}$ which acts diagonally. We have that 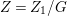 $Z=Z_{1}/G$ is a klt rationally connected surface such that
$Z=Z_{1}/G$ is a klt rationally connected surface such that ![]() $K_{Z}$ is
$K_{Z}$ is ![]() $\mathbb{Q}$-linearly equivalent to the zero divisor (see [Reference TotaroTot12, Example 10]). Let
$\mathbb{Q}$-linearly equivalent to the zero divisor (see [Reference TotaroTot12, Example 10]). Let 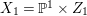 $X_{1}=\mathbb{P}^{1}\times Z_{1}$ and define an action of
$X_{1}=\mathbb{P}^{1}\times Z_{1}$ and define an action of ![]() $G$ on
$G$ on ![]() $\mathbb{P}^{1}$ by
$\mathbb{P}^{1}$ by 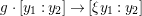 $g\cdot [y_{1}:y_{2}]\rightarrow [{\it\xi}y_{1}:y_{2}]$, where
$g\cdot [y_{1}:y_{2}]\rightarrow [{\it\xi}y_{1}:y_{2}]$, where ![]() $[y_{1}:y_{2}]$ are homogeneous coordinates of
$[y_{1}:y_{2}]$ are homogeneous coordinates of ![]() $\mathbb{P}^{1}$. Then there is an induced action of
$\mathbb{P}^{1}$. Then there is an induced action of ![]() $G$ on the smooth threefold
$G$ on the smooth threefold ![]() $X_{1}$ which acts diagonally. Since
$X_{1}$ which acts diagonally. Since 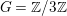 $G=\mathbb{Z}/3\mathbb{Z}$ and this action is free in codimension
$G=\mathbb{Z}/3\mathbb{Z}$ and this action is free in codimension ![]() $2$, this action satisfies the condition of [Reference ReidRei80, Theorem 3.1]. Hence,
$2$, this action satisfies the condition of [Reference ReidRei80, Theorem 3.1]. Hence, 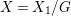 $X=X_{1}/G$ has canonical singularities. We also have a Mori fibration
$X=X_{1}/G$ has canonical singularities. We also have a Mori fibration ![]() $X\rightarrow Z$ whose general fibers are isomorphic to
$X\rightarrow Z$ whose general fibers are isomorphic to ![]() $\mathbb{P}^{1}$. Since
$\mathbb{P}^{1}$. Since ![]() $Z$ is rationally connected, so is
$Z$ is rationally connected, so is ![]() $X$ by [Reference Graber, Harris and StarrGHS03, Theorem 1.1]. Moreover, since
$X$ by [Reference Graber, Harris and StarrGHS03, Theorem 1.1]. Moreover, since ![]() $K_{Z}$ is
$K_{Z}$ is ![]() $\mathbb{Q}$-effective, we have
$\mathbb{Q}$-effective, we have 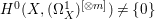 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some ![]() $m>0$ (see Section 4.2).
$m>0$ (see Section 4.2).
In the example above, the non-zero pluri-forms come from ![]() $K_{Z}$, the canonical divisor of the base surface. In the following example,
$K_{Z}$, the canonical divisor of the base surface. In the following example, ![]() $-K_{Z}$ is ample. However,
$-K_{Z}$ is ample. However, ![]() $X$ still carries non-zero pluri-forms. These forms come from the multiple fibers of the fibration
$X$ still carries non-zero pluri-forms. These forms come from the multiple fibers of the fibration ![]() $X\rightarrow Z$. Before giving the example, we first introduce a method to construct non-reduced fibers.
$X\rightarrow Z$. Before giving the example, we first introduce a method to construct non-reduced fibers.
Construction 2.13. We want to construct a fibration ![]() $p$ from a normal threefold
$p$ from a normal threefold ![]() $T$ with canonical singularities to a smooth surface
$T$ with canonical singularities to a smooth surface ![]() $S$ such that
$S$ such that 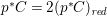 $p^{\ast }C=2(p^{\ast }C)_{\mathit{red}}$, where
$p^{\ast }C=2(p^{\ast }C)_{\mathit{red}}$, where ![]() $C$ is a smooth curve in
$C$ is a smooth curve in ![]() $S$.
$S$.
Let 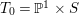 $T_{0}=\mathbb{P}^{1}\times S$, where
$T_{0}=\mathbb{P}^{1}\times S$, where ![]() $S$ is a smooth projective surface. Let
$S$ is a smooth projective surface. Let ![]() $p_{1}$,
$p_{1}$, ![]() $p_{2}$ be the natural projections
$p_{2}$ be the natural projections 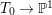 $T_{0}\rightarrow \mathbb{P}^{1}$ and
$T_{0}\rightarrow \mathbb{P}^{1}$ and ![]() $T_{0}\rightarrow S$. Let
$T_{0}\rightarrow S$. Let ![]() $C\subseteq S$ be a smooth curve, and let
$C\subseteq S$ be a smooth curve, and let 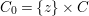 $C_{0}=\{z\}\times C$ be a section of
$C_{0}=\{z\}\times C$ be a section of ![]() $p_{2}$ over
$p_{2}$ over ![]() $C$ in
$C$ in ![]() $T_{0}$, where
$T_{0}$, where ![]() $z$ is a point of
$z$ is a point of ![]() $\mathbb{P}^{1}$. Let
$\mathbb{P}^{1}$. Let 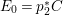 $E_{0}=p_{2}^{\ast }C$, which is a smooth divisor in
$E_{0}=p_{2}^{\ast }C$, which is a smooth divisor in ![]() $T_{0}$. We perform a sequence of birational transformations of
$T_{0}$. We perform a sequence of birational transformations of ![]() $T_{0}$.
$T_{0}$.
First, we blow up ![]() $C_{0}$, and we obtain a morphism
$C_{0}$, and we obtain a morphism 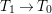 $T_{1}\rightarrow T_{0}$ with exceptional divisor
$T_{1}\rightarrow T_{0}$ with exceptional divisor ![]() $E_{1}$. Denote still by
$E_{1}$. Denote still by ![]() $E_{0}$ the strict transform of
$E_{0}$ the strict transform of ![]() $E_{0}$ in
$E_{0}$ in ![]() $T_{1}$. If
$T_{1}$. If ![]() $F$ is a fiber of
$F$ is a fiber of ![]() $T_{1}\rightarrow S$ over a point of
$T_{1}\rightarrow S$ over a point of ![]() $C$, then
$C$, then 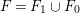 $F=F_{1}\cup F_{0}$, where
$F=F_{1}\cup F_{0}$, where ![]() $F_{i}\subseteq E_{i}$ are rational curves and
$F_{i}\subseteq E_{i}$ are rational curves and 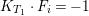 $K_{T_{1}}\cdot F_{i}=-1$,
$K_{T_{1}}\cdot F_{i}=-1$, 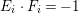 $E_{i}\cdot F_{i}=-1$.
$E_{i}\cdot F_{i}=-1$.
Now we blow up ![]() $C_{1}$, the intersection of
$C_{1}$, the intersection of ![]() $E_{0}$ and
$E_{0}$ and ![]() $E_{1}$. We obtain a morphism
$E_{1}$. We obtain a morphism 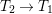 $T_{2}\rightarrow T_{1}$ with exceptional divisor
$T_{2}\rightarrow T_{1}$ with exceptional divisor ![]() $E_{2}$. Denote still by
$E_{2}$. Denote still by ![]() $E_{0}$,
$E_{0}$, ![]() $E_{1}$ the strict transforms of
$E_{1}$ the strict transforms of ![]() $E_{0}$ and
$E_{0}$ and ![]() $E_{1}$ in
$E_{1}$ in ![]() $T_{2}$. If
$T_{2}$. If ![]() $F$ is any set-theoretic fiber of
$F$ is any set-theoretic fiber of ![]() $T_{2}\rightarrow S$ over a point of
$T_{2}\rightarrow S$ over a point of ![]() $C$, then
$C$, then 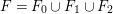 $F=F_{0}\cup F_{1}\cup F_{2}$, where
$F=F_{0}\cup F_{1}\cup F_{2}$, where ![]() $F_{i}\subseteq E_{i}$ are rational curves and
$F_{i}\subseteq E_{i}$ are rational curves and 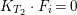 $K_{T_{2}}\cdot F_{i}=0$,
$K_{T_{2}}\cdot F_{i}=0$, 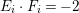 $E_{i}\cdot F_{i}=-2$ for
$E_{i}\cdot F_{i}=-2$ for ![]() $i=0,1$,
$i=0,1$, 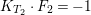 $K_{T_{2}}\cdot F_{2}=-1$,
$K_{T_{2}}\cdot F_{2}=-1$, 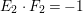 $E_{2}\cdot F_{2}=-1$. Let
$E_{2}\cdot F_{2}=-1$. Let ![]() $q$ be the fibration
$q$ be the fibration ![]() $T_{2}\rightarrow S$.
$T_{2}\rightarrow S$.
We blow down ![]() $E_{1}$ and
$E_{1}$ and ![]() $E_{0}$ in
$E_{0}$ in ![]() $T_{2}$. Let
$T_{2}$. Let ![]() $H$ be an ample
$H$ be an ample ![]() $\mathbb{Q}$-divisor such that
$\mathbb{Q}$-divisor such that 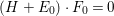 $(H+E_{0})\cdot F_{0}=0$. Since
$(H+E_{0})\cdot F_{0}=0$. Since 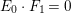 $E_{0}\cdot F_{1}=0$, there is a positive rational number
$E_{0}\cdot F_{1}=0$, there is a positive rational number ![]() $b$ such that
$b$ such that 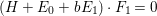 $(H+E_{0}+bE_{1})\cdot F_{1}=0$. Moreover,
$(H+E_{0}+bE_{1})\cdot F_{1}=0$. Moreover, 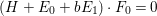 $(H+E_{0}+bE_{1})\cdot F_{0}=0$ since
$(H+E_{0}+bE_{1})\cdot F_{0}=0$ since 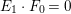 $E_{1}\cdot F_{0}=0$. Let
$E_{1}\cdot F_{0}=0$. Let ![]() $A$ be a sufficiently ample divisor on
$A$ be a sufficiently ample divisor on ![]() $S$. Then the
$S$. Then the ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor 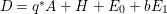 $D=q^{\ast }A+H+E_{0}+bE_{1}$ is nef and big. Moreover, any curve
$D=q^{\ast }A+H+E_{0}+bE_{1}$ is nef and big. Moreover, any curve ![]() $B$ which has intersection number
$B$ which has intersection number ![]() $0$ with
$0$ with ![]() $D$ must be contracted by
$D$ must be contracted by ![]() $T_{2}\rightarrow S$ since
$T_{2}\rightarrow S$ since ![]() $A$ is sufficiently ample. The curve
$A$ is sufficiently ample. The curve ![]() $B$ is also contained in
$B$ is also contained in 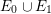 $E_{0}\cup E_{1}$ since
$E_{0}\cup E_{1}$ since ![]() $H$ is ample. Since
$H$ is ample. Since 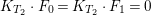 $K_{T_{2}}\cdot F_{0}=K_{T_{2}}\cdot F_{1}=0$, there exists a large integer
$K_{T_{2}}\cdot F_{0}=K_{T_{2}}\cdot F_{1}=0$, there exists a large integer ![]() $k$ such that
$k$ such that 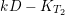 $kD-K_{T_{2}}$ is nef and big. Then, by the basepoint-free theorem (see [Reference Kollár and MoriKM98, Theorem 3.3]), there is a large enough integer
$kD-K_{T_{2}}$ is nef and big. Then, by the basepoint-free theorem (see [Reference Kollár and MoriKM98, Theorem 3.3]), there is a large enough integer ![]() $a$ such that
$a$ such that ![]() $aD$ is Cartier and
$aD$ is Cartier and ![]() $|aD|$ is basepoint-free. The linear system
$|aD|$ is basepoint-free. The linear system ![]() $|aD|$ induces a contraction which contracts
$|aD|$ induces a contraction which contracts ![]() $E_{0}$ and
$E_{0}$ and ![]() $E_{1}$.
$E_{1}$.
By contracting ![]() $E_{0}$ and
$E_{0}$ and ![]() $E_{1}$, we obtain a threefold
$E_{1}$, we obtain a threefold ![]() $T$. Moreover, there is an induced fibration
$T$. Moreover, there is an induced fibration 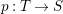 $p:T\rightarrow S$ such that
$p:T\rightarrow S$ such that 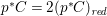 $p^{\ast }C=2(p^{\ast }C)_{\mathit{red}}$. Note that
$p^{\ast }C=2(p^{\ast }C)_{\mathit{red}}$. Note that ![]() $T_{2}\rightarrow T$ is a resolution of singularities and
$T_{2}\rightarrow T$ is a resolution of singularities and 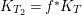 $K_{T_{2}}=f^{\ast }K_{T}$. Hence,
$K_{T_{2}}=f^{\ast }K_{T}$. Hence, ![]() $V$ has canonical singularities.
$V$ has canonical singularities.
Now we construct the example.
Example 2.14. Let 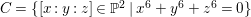 $C=\{[x:y:z]\in \mathbb{P}^{2}\mid x^{6}+y^{6}+z^{6}=0\}$ be a smooth curve in
$C=\{[x:y:z]\in \mathbb{P}^{2}\mid x^{6}+y^{6}+z^{6}=0\}$ be a smooth curve in ![]() $\mathbb{P}^{2}$. Then
$\mathbb{P}^{2}$. Then 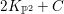 $2K_{\mathbb{P}^{2}}+C$ is linearly equivalent to the zero divisor. Let
$2K_{\mathbb{P}^{2}}+C$ is linearly equivalent to the zero divisor. Let 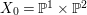 $X_{0}=\mathbb{P}^{1}\times \mathbb{P}^{2}$. By the method of Construction 2.13, we can construct a fiber space
$X_{0}=\mathbb{P}^{1}\times \mathbb{P}^{2}$. By the method of Construction 2.13, we can construct a fiber space 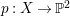 $p:X\rightarrow \mathbb{P}^{2}$ such that
$p:X\rightarrow \mathbb{P}^{2}$ such that 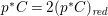 $p^{\ast }C=2(p^{\ast }C)_{\mathit{red}}$. Then
$p^{\ast }C=2(p^{\ast }C)_{\mathit{red}}$. Then ![]() $X$ has canonical singularities. Since general fibers of
$X$ has canonical singularities. Since general fibers of ![]() $p$ are isomorphic to
$p$ are isomorphic to ![]() $\mathbb{P}^{1}$,
$\mathbb{P}^{1}$, ![]() $X$ is rationally connected by [Reference Graber, Harris and StarrGHS03, Theorem 1.1]. Moreover, since
$X$ is rationally connected by [Reference Graber, Harris and StarrGHS03, Theorem 1.1]. Moreover, since 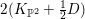 $2(K_{\mathbb{P}^{2}}+\frac{1}{2}D)$ is an effective divisor and
$2(K_{\mathbb{P}^{2}}+\frac{1}{2}D)$ is an effective divisor and ![]() $p$ is equidimensional, we have
$p$ is equidimensional, we have 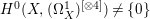 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes 4]})\neq \{0\}$ (see Section 4.2).
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes 4]})\neq \{0\}$ (see Section 4.2).
Note that in the three examples above, the variety ![]() $X$ we constructed is a rationally connected variety with canonical singularities. The divisor
$X$ we constructed is a rationally connected variety with canonical singularities. The divisor ![]() $K_{X}$ is not pseudo-effective and we always have a Mori fibration from
$K_{X}$ is not pseudo-effective and we always have a Mori fibration from ![]() $X$ to a variety
$X$ to a variety ![]() $Z$. The non-zero pluri-forms of
$Z$. The non-zero pluri-forms of ![]() $X$ come from the base
$X$ come from the base ![]() $Z$. However, in the following example, the variety we construct is a rationally connected threefold with klt singularities whose canonical divisor is ample. Some non-zero pluri-forms come from its canonical divisor.
$Z$. However, in the following example, the variety we construct is a rationally connected threefold with klt singularities whose canonical divisor is ample. Some non-zero pluri-forms come from its canonical divisor.
Example 2.15. Let ![]() $X_{1}$ be the Fermat hypersurface in
$X_{1}$ be the Fermat hypersurface in ![]() $\mathbb{P}^{4}$ defined
$\mathbb{P}^{4}$ defined 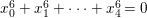 $x_{0}^{6}+x_{1}^{6}+\cdots +x_{4}^{6}=0$. Then
$x_{0}^{6}+x_{1}^{6}+\cdots +x_{4}^{6}=0$. Then ![]() $X_{1}$ is a smooth threefold such that
$X_{1}$ is a smooth threefold such that ![]() $K_{X_{1}}$ is ample. Moreover, the Picard number of
$K_{X_{1}}$ is ample. Moreover, the Picard number of ![]() $X_{1}$ is
$X_{1}$ is ![]() $1$ by the Lefschetz theorem (see [Reference LazarsfeldLaz04, Example 3.1.23]). Let
$1$ by the Lefschetz theorem (see [Reference LazarsfeldLaz04, Example 3.1.23]). Let ![]() $G$ be the group
$G$ be the group ![]() $\mathbb{Z}/6\mathbb{Z}$ with generator
$\mathbb{Z}/6\mathbb{Z}$ with generator ![]() $g$. Define an action of
$g$. Define an action of ![]() $G$ on
$G$ on ![]() $\mathbb{P}^{4}$ by
$\mathbb{P}^{4}$ by 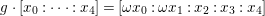 $g\cdot [x_{0}:\cdots :x_{4}]=[{\it\omega}x_{0}:{\it\omega}x_{1}:x_{2}:x_{3}:x_{4}]$, where
$g\cdot [x_{0}:\cdots :x_{4}]=[{\it\omega}x_{0}:{\it\omega}x_{1}:x_{2}:x_{3}:x_{4}]$, where ![]() ${\it\omega}$ is a primitive sixth root of unity. This action induces an action of
${\it\omega}$ is a primitive sixth root of unity. This action induces an action of ![]() $G$ on
$G$ on ![]() $X_{1}$ which is free in codimension
$X_{1}$ which is free in codimension ![]() $1$. Denote the quotient
$1$. Denote the quotient ![]() $X_{1}/G$ by
$X_{1}/G$ by ![]() $X$ and the natural morphism
$X$ and the natural morphism 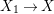 $X_{1}\rightarrow X$ by
$X_{1}\rightarrow X$ by ![]() ${\it\pi}$. Then
${\it\pi}$. Then ![]() $X$ has
$X$ has ![]() $\mathbb{Q}$-factorial klt singularities but does not have canonical singularities (see [Reference ReidRei80, Theorem 3.1]). Now we prove that
$\mathbb{Q}$-factorial klt singularities but does not have canonical singularities (see [Reference ReidRei80, Theorem 3.1]). Now we prove that ![]() $X$ is rationally connected. First, we prove that
$X$ is rationally connected. First, we prove that ![]() $X$ is uniruled. If
$X$ is uniruled. If ![]() $w$ is a general point in
$w$ is a general point in ![]() $X$, then there is a point
$X$, then there is a point 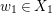 $w_{1}\in X_{1}$ such that
$w_{1}\in X_{1}$ such that 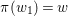 ${\it\pi}(w_{1})=w$ and the first two coordinates of
${\it\pi}(w_{1})=w$ and the first two coordinates of ![]() $w_{1}$ are both non-zero. There are two hyperplanes in
$w_{1}$ are both non-zero. There are two hyperplanes in ![]() $\mathbb{P}^{4}$ passing through
$\mathbb{P}^{4}$ passing through ![]() $w_{1}$,
$w_{1}$, 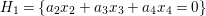 $H_{1}=\{a_{2}x_{2}+a_{3}x_{3}+a_{4}x_{4}=0\}$ and
$H_{1}=\{a_{2}x_{2}+a_{3}x_{3}+a_{4}x_{4}=0\}$ and 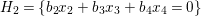 $H_{2}=\{b_{2}x_{2}+b_{3}x_{3}+b_{4}x_{4}=0\}$, such that the intersection
$H_{2}=\{b_{2}x_{2}+b_{3}x_{3}+b_{4}x_{4}=0\}$, such that the intersection 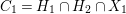 $C_{1}=H_{1}\cap H_{2}\cap X_{1}$ is a smooth curve of genus
$C_{1}=H_{1}\cap H_{2}\cap X_{1}$ is a smooth curve of genus ![]() $10$. Moreover, there are exactly
$10$. Moreover, there are exactly ![]() $6$ points on
$6$ points on ![]() $C_{1}$, given by
$C_{1}$, given by 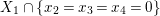 $X_{1}\cap \{x_{2}=x_{3}=x_{4}=0\}$, which are fixed under the action of
$X_{1}\cap \{x_{2}=x_{3}=x_{4}=0\}$, which are fixed under the action of ![]() $G$. Hence,
$G$. Hence, 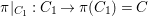 ${\it\pi}|_{C_{1}}:C_{1}\rightarrow {\it\pi}(C_{1})=C$ is ramified exactly at those
${\it\pi}|_{C_{1}}:C_{1}\rightarrow {\it\pi}(C_{1})=C$ is ramified exactly at those ![]() $6$ points with degree
$6$ points with degree ![]() $6$. By the ramification formula,
$6$. By the ramification formula, 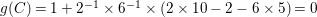 $g(C)=1+2^{-1}\times 6^{-1}\times (2\times 10-2-6\times 5)=0$, where
$g(C)=1+2^{-1}\times 6^{-1}\times (2\times 10-2-6\times 5)=0$, where ![]() $g(C)$ is the genus of
$g(C)$ is the genus of ![]() $C$. Hence,
$C$. Hence, ![]() $C$ is a smooth rational curve. This implies that
$C$ is a smooth rational curve. This implies that ![]() $X$ is uniruled. Since
$X$ is uniruled. Since ![]() $X$ has Picard number
$X$ has Picard number ![]() $1$, from the lemma below, we conclude that
$1$, from the lemma below, we conclude that ![]() $X$ is rationally connected.
$X$ is rationally connected.
Lemma 2.16. Let ![]() $X$ be a normal projective variety which is
$X$ be a normal projective variety which is ![]() $\mathbb{Q}$-factorial. Assume that the Picard number of
$\mathbb{Q}$-factorial. Assume that the Picard number of ![]() $X$ is
$X$ is ![]() $1$. Then
$1$. Then ![]() $X$ is rationally connected if and only if it is uniruled.
$X$ is rationally connected if and only if it is uniruled.
Proof. Assume that ![]() $X$ is uniruled and let
$X$ is uniruled and let 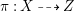 ${\it\pi}:X{\dashrightarrow}Z$ be the MRC fibration for
${\it\pi}:X{\dashrightarrow}Z$ be the MRC fibration for ![]() $X$ (see, for example, [Reference KollárKol96, Theorem V.5.2]). We argue by contradiction. Assume that
$X$ (see, for example, [Reference KollárKol96, Theorem V.5.2]). We argue by contradiction. Assume that 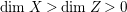 $\text{dim}\,X>\text{dim}\,Z>0$. Then there is a Zariski open subset
$\text{dim}\,X>\text{dim}\,Z>0$. Then there is a Zariski open subset ![]() $Z_{0}$ of
$Z_{0}$ of ![]() $Z$ such that
$Z$ such that ![]() ${\it\pi}$ is regular and proper over
${\it\pi}$ is regular and proper over ![]() $Z_{0}$. Let
$Z_{0}$. Let ![]() $C$ be a curve contained in some fiber of
$C$ be a curve contained in some fiber of ![]() ${\it\pi}|_{Z_{0}}$. Let
${\it\pi}|_{Z_{0}}$. Let ![]() $D$ be a non-zero effective Cartier divisor on
$D$ be a non-zero effective Cartier divisor on ![]() $Z_{0}$. Let
$Z_{0}$. Let 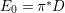 $E_{0}={\it\pi}^{\ast }D$. Then
$E_{0}={\it\pi}^{\ast }D$. Then ![]() $E_{0}$ is a non-zero effective divisor on
$E_{0}$ is a non-zero effective divisor on 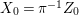 $X_{0}={\it\pi}^{-1}Z_{0}$. Let
$X_{0}={\it\pi}^{-1}Z_{0}$. Let ![]() $E$ be the closure of
$E$ be the closure of ![]() $E_{0}$ in
$E_{0}$ in ![]() $X$, then
$X$, then ![]() $E$ is a non-zero effective
$E$ is a non-zero effective ![]() $\mathbb{Q}$-Cartier Weil divisor on
$\mathbb{Q}$-Cartier Weil divisor on ![]() $X$. However, the intersection number of
$X$. However, the intersection number of ![]() $E$ and
$E$ and ![]() $C$ is zero, which contradicts the fact that
$C$ is zero, which contradicts the fact that ![]() $X$ has Picard number
$X$ has Picard number ![]() $1$.◻
$1$.◻
3 Fibrations over curves
3.1 Construction of rationally connected varieties carrying non-zero pluri-forms
In this subsection, we give a method to construct rationally connected varieties which carry non-zero pluri-forms (Theorem 3.2). Together with Theorem 1.4, we see that every rationally connected threefold with ![]() $\mathbb{Q}$-factorial terminal singularities which carries non-zero pluri-forms can be constructed by this method.
$\mathbb{Q}$-factorial terminal singularities which carries non-zero pluri-forms can be constructed by this method.
By Lemma 2.5, if general fibers of an equidimensional fibration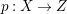 $p:X\rightarrow Z$ do not carry any non-zero pluri-forms, then for all
$p:X\rightarrow Z$ do not carry any non-zero pluri-forms, then for all ![]() $m>0$, we have
$m>0$, we have 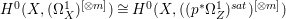 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]})$. Moreover,
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]})$. Moreover,
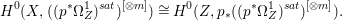 $$\begin{eqnarray}H^{0}(X,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]})\cong H^{0}(Z,p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]}).\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(X,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]})\cong H^{0}(Z,p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]}).\end{eqnarray}$$ Hence, we would like to know what 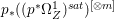 $p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]}$ is. In the case when
$p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]}$ is. In the case when ![]() $Z$ is a smooth curve, this is not difficult to compute. Note that if
$Z$ is a smooth curve, this is not difficult to compute. Note that if ![]() $R$ is the ramification divisor of
$R$ is the ramification divisor of ![]() $p$, then
$p$, then 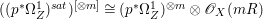 $((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]}\cong (p^{\ast }{\rm\Omega}_{Z}^{1})^{\otimes m}\otimes \mathscr{O}_{X}(mR)$ for
$((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]}\cong (p^{\ast }{\rm\Omega}_{Z}^{1})^{\otimes m}\otimes \mathscr{O}_{X}(mR)$ for ![]() $m>0$. By the projection formula, we have
$m>0$. By the projection formula, we have
 $$\begin{eqnarray}p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]}\cong ({\rm\Omega}_{Z}^{1})^{\otimes m}\otimes p_{\ast }\mathscr{O}_{X}(mR).\end{eqnarray}$$
$$\begin{eqnarray}p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]}\cong ({\rm\Omega}_{Z}^{1})^{\otimes m}\otimes p_{\ast }\mathscr{O}_{X}(mR).\end{eqnarray}$$ Hence, it is sufficient to compute 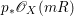 $p_{\ast }\mathscr{O}_{X}(mR)$.
$p_{\ast }\mathscr{O}_{X}(mR)$.
Lemma 3.1. Let 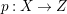 $p:X\rightarrow Z$ be a fibration from a normal variety to a smooth curve. Let
$p:X\rightarrow Z$ be a fibration from a normal variety to a smooth curve. Let ![]() $z$ be a point in
$z$ be a point in ![]() $Z$. Let
$Z$. Let 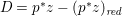 $D=p^{\ast }z-(p^{\ast }z)_{\mathit{red}}$. Then
$D=p^{\ast }z-(p^{\ast }z)_{\mathit{red}}$. Then 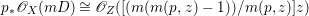 $p_{\ast }\mathscr{O}_{X}(mD)\cong \mathscr{O}_{Z}([(m(m(p,z)-1))/m(p,z)]z)$ for any
$p_{\ast }\mathscr{O}_{X}(mD)\cong \mathscr{O}_{Z}([(m(m(p,z)-1))/m(p,z)]z)$ for any ![]() $m\geqslant 0$.
$m\geqslant 0$.
Proof. The problem is local and we may assume that ![]() $Z$ is affine. We know that
$Z$ is affine. We know that 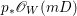 $p_{\ast }\mathscr{O}_{W}(mD)$ is an invertible sheaf. If
$p_{\ast }\mathscr{O}_{W}(mD)$ is an invertible sheaf. If ![]() ${\it\theta}$ is a section of
${\it\theta}$ is a section of 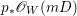 $p_{\ast }\mathscr{O}_{W}(mD)$, then it is a rational function on
$p_{\ast }\mathscr{O}_{W}(mD)$, then it is a rational function on ![]() $Z$ whose pullback on
$Z$ whose pullback on ![]() $W$ is a rational function which can only have a pole along
$W$ is a rational function which can only have a pole along ![]() $p^{\ast }z$. Hence,
$p^{\ast }z$. Hence, ![]() ${\it\theta}$ can only have a pole at
${\it\theta}$ can only have a pole at ![]() $z$. Let
$z$. Let ![]() $d_{}$ be the degree of the pole, then the pullback of
$d_{}$ be the degree of the pole, then the pullback of ![]() ${\it\theta}$ in
${\it\theta}$ in ![]() $V$ is a section of
$V$ is a section of 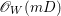 $\mathscr{O}_{W}(mD)$ if and only if
$\mathscr{O}_{W}(mD)$ if and only if 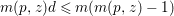 $m(p,z)d_{}\leqslant m(m(p,z)-1)$, that is,
$m(p,z)d_{}\leqslant m(m(p,z)-1)$, that is,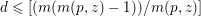 $d_{}\leqslant [(m(m(p,z)-1))/m(p,z)]$.◻
$d_{}\leqslant [(m(m(p,z)-1))/m(p,z)]$.◻
This relation between ramification divisor and pluri-forms gives us an idea of how to construct rationally connected varieties which carry non-zero pluri-forms. Note that if 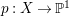 $p:X\rightarrow \mathbb{P}^{1}$ is a fibration such that general fibers of
$p:X\rightarrow \mathbb{P}^{1}$ is a fibration such that general fibers of ![]() $p$ are rationally connected, then
$p$ are rationally connected, then ![]() $X$ is rationally connected by [Reference Graber, Harris and StarrGHS03, Theorem 1.1]. Moreover, if general fibers of
$X$ is rationally connected by [Reference Graber, Harris and StarrGHS03, Theorem 1.1]. Moreover, if general fibers of ![]() $p$ do not carry any non-zero pluri-forms, then from the discussion above,
$p$ do not carry any non-zero pluri-forms, then from the discussion above, ![]() $X$ carries non-zero pluri-forms if and only if
$X$ carries non-zero pluri-forms if and only if 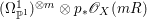 $({\rm\Omega}_{\mathbb{P}^{1}}^{1})^{\otimes m}\otimes p_{\ast }\mathscr{O}_{X}(mR)$ has non-zero sections for some
$({\rm\Omega}_{\mathbb{P}^{1}}^{1})^{\otimes m}\otimes p_{\ast }\mathscr{O}_{X}(mR)$ has non-zero sections for some ![]() $m>0$, where
$m>0$, where ![]() $R$ is the ramification divisor of
$R$ is the ramification divisor of ![]() $p$. However,
$p$. However, 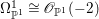 ${\rm\Omega}_{\mathbb{P}^{1}}^{1}\cong \mathscr{O}_{\mathbb{P}^{1}}(-2)$ and
${\rm\Omega}_{\mathbb{P}^{1}}^{1}\cong \mathscr{O}_{\mathbb{P}^{1}}(-2)$ and 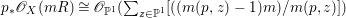 $p_{\ast }\mathscr{O}_{X}(mR)\cong \mathscr{O}_{\mathbb{P}^{1}}(\sum _{z\in \mathbb{P}^{1}}[((m(p,z)-1)m)/m(p,z)])$, since any two points in
$p_{\ast }\mathscr{O}_{X}(mR)\cong \mathscr{O}_{\mathbb{P}^{1}}(\sum _{z\in \mathbb{P}^{1}}[((m(p,z)-1)m)/m(p,z)])$, since any two points in ![]() $\mathbb{P}^{1}$ are linearly equivalent. Hence,
$\mathbb{P}^{1}$ are linearly equivalent. Hence, ![]() $X$ carries non-zero pluri-forms if and only if
$X$ carries non-zero pluri-forms if and only if 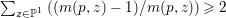 $\sum _{z\in \mathbb{P}^{1}}((m(p,z)-1)/m(p,z))\geqslant 2$.
$\sum _{z\in \mathbb{P}^{1}}((m(p,z)-1)/m(p,z))\geqslant 2$.
Now we try to construct this kind of varieties by taking quotients. Let ![]() $T$ be a normal projective variety, let
$T$ be a normal projective variety, let ![]() $B$ be a smooth projective curve, and let
$B$ be a smooth projective curve, and let ![]() $G$ be a finite commutative group. Assume that there are actions of
$G$ be a finite commutative group. Assume that there are actions of ![]() $G$ on
$G$ on ![]() $T$ and
$T$ and ![]() $B$. Assume that there is a
$B$. Assume that there is a ![]() $G$-equivariant fibration
$G$-equivariant fibration 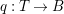 $q:T\rightarrow B$. Let
$q:T\rightarrow B$. Let 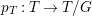 $p_{T}:T\rightarrow T/G$,
$p_{T}:T\rightarrow T/G$, 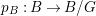 $p_{B}:B\rightarrow B/G$ be natural projections and let
$p_{B}:B\rightarrow B/G$ be natural projections and let 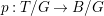 $p:T/G\rightarrow B/G$ be the induced fibration. Let
$p:T/G\rightarrow B/G$ be the induced fibration. Let ![]() $S_{i}$,
$S_{i}$, 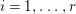 $i=1,\ldots ,r$ be all the
$i=1,\ldots ,r$ be all the ![]() $G$-orbits in
$G$-orbits in ![]() $B$ whose cardinality is less than the cardinality of
$B$ whose cardinality is less than the cardinality of ![]() $G$. Let
$G$. Let ![]() $z_{i}$ be the image of
$z_{i}$ be the image of ![]() $S_{i}$ under the map
$S_{i}$ under the map 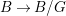 $B\rightarrow B/G$. Then the
$B\rightarrow B/G$. Then the ![]() $z_{i}$ are the points in
$z_{i}$ are the points in ![]() $B/G$ over which
$B/G$ over which 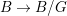 $B\rightarrow B/G$ is ramified. Let
$B\rightarrow B/G$ is ramified. Let ![]() $G_{i}$ be the stabilizer of a point
$G_{i}$ be the stabilizer of a point ![]() $b_{i}$ in
$b_{i}$ in ![]() $S_{i}$. Then
$S_{i}$. Then ![]() $G_{i}$ acts on the set-theoretic fiber
$G_{i}$ acts on the set-theoretic fiber 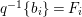 $q^{-1}\{b_{i}\}=F_{i}$. If
$q^{-1}\{b_{i}\}=F_{i}$. If ![]() $A_{i}$ is a component in
$A_{i}$ is a component in ![]() $F_{i}$ and the stabilizer of a general point in
$F_{i}$ and the stabilizer of a general point in ![]() $A_{i}$ has cardinality
$A_{i}$ has cardinality ![]() $d_{i}$, then
$d_{i}$, then ![]() $p_{T}$ is ramified along
$p_{T}$ is ramified along ![]() $G_{i}\cdot A_{i}$ of degree
$G_{i}\cdot A_{i}$ of degree ![]() $d_{i}$, where
$d_{i}$, where ![]() $G_{i}\cdot A_{i}$ is the orbit of
$G_{i}\cdot A_{i}$ is the orbit of ![]() $A_{i}$ under
$A_{i}$ under ![]() $G_{i}$. In this case,
$G_{i}$. In this case, ![]() $p_{T}(A_{i})$ has coefficient
$p_{T}(A_{i})$ has coefficient ![]() $e_{i}f_{i}/d_{i}$ in
$e_{i}f_{i}/d_{i}$ in ![]() $p^{\ast }z_{i}$, where
$p^{\ast }z_{i}$, where ![]() $e_{i}$ is the coefficient of
$e_{i}$ is the coefficient of ![]() $A_{i}$ in
$A_{i}$ in ![]() $q^{\ast }b_{i}$ and
$q^{\ast }b_{i}$ and ![]() $f_{i}$ is the cardinality of
$f_{i}$ is the cardinality of ![]() $G_{i}$. Denote
$G_{i}$. Denote 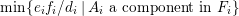 $\min \{e_{i}f_{i}/d_{i}\mid A_{i}~\text{a component in}~F_{i}\}$ by
$\min \{e_{i}f_{i}/d_{i}\mid A_{i}~\text{a component in}~F_{i}\}$ by ![]() $s_{i}$. Then
$s_{i}$. Then ![]() $s_{i}$ is equal to
$s_{i}$ is equal to 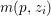 $m(p,z_{i})$. We have the following theorem.
$m(p,z_{i})$. We have the following theorem.
Theorem 3.2. Let ![]() $T$ be a projective normal variety, let
$T$ be a projective normal variety, let ![]() $B$ be a projective smooth curve with positive genus, and let
$B$ be a projective smooth curve with positive genus, and let ![]() $G$ be a finite commutative group. Assume that they satisfy the following conditions.
$G$ be a finite commutative group. Assume that they satisfy the following conditions.
(1) There is a fibration
 $q$ from
$q$ from  $T$ to
$T$ to  $B$ such that for any general fiber
$B$ such that for any general fiber  $F_{q}$ of
$F_{q}$ of  $q$,
$q$,  $F_{q}$ is rationally connected and does not carry any non-zero pluri-forms. Moreover,
$F_{q}$ is rationally connected and does not carry any non-zero pluri-forms. Moreover,  $m(q,b)=1$ for all
$m(q,b)=1$ for all  $b\in B$.
$b\in B$.(2) There exist actions of
 $G$ on
$G$ on  $B$ and on
$B$ and on  $T$ such that
$T$ such that  $q$ is
$q$ is  $G$-equivariant.
$G$-equivariant.(3) The quotient
 $B/G$ is isomorphic to
$B/G$ is isomorphic to  $\mathbb{P}^{1}$.
$\mathbb{P}^{1}$.
Then the quotient 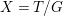 $X=T/G$ is a normal projective rationally connected variety and there is a fibration
$X=T/G$ is a normal projective rationally connected variety and there is a fibration 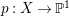 $p:X\rightarrow \mathbb{P}^{1}$. Moreover, if we define
$p:X\rightarrow \mathbb{P}^{1}$. Moreover, if we define ![]() $s_{i}$,
$s_{i}$, 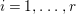 $i=1,\ldots ,r$ as above, then
$i=1,\ldots ,r$ as above, then ![]() $X$ carries non-zero pluri-forms if and only if
$X$ carries non-zero pluri-forms if and only if 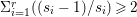 ${\rm\Sigma}_{i=1}^{r}((s_{i}-1)/s_{i})\geqslant 2$. More precisely,
${\rm\Sigma}_{i=1}^{r}((s_{i}-1)/s_{i})\geqslant 2$. More precisely,
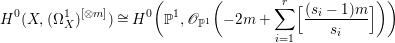 $$\begin{eqnarray}H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}\biggl(\mathbb{P}^{1},\mathscr{O}_{\mathbb{ P}^{1}}\biggl(-2m+\mathop{\sum }_{i=1}^{r}[\frac{(s_{i}-1)m}{s_{i}}]\biggr)\biggr)\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}\biggl(\mathbb{P}^{1},\mathscr{O}_{\mathbb{ P}^{1}}\biggl(-2m+\mathop{\sum }_{i=1}^{r}[\frac{(s_{i}-1)m}{s_{i}}]\biggr)\biggr)\end{eqnarray}$$ for ![]() $m>0$.
$m>0$.
Proof. The fibration 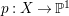 $p:X\rightarrow \mathbb{P}^{1}$ is induced by
$p:X\rightarrow \mathbb{P}^{1}$ is induced by ![]() $q$. Since general fibers of
$q$. Since general fibers of ![]() $q$ are rationally connected, general fibers of
$q$ are rationally connected, general fibers of ![]() $p$ are also rationally connected. Hence,
$p$ are also rationally connected. Hence, ![]() $X$ is rationally connected by [Reference Graber, Harris and StarrGHS03, Theorem 1.1]. If
$X$ is rationally connected by [Reference Graber, Harris and StarrGHS03, Theorem 1.1]. If ![]() $F_{p}$ is a general fiber of
$F_{p}$ is a general fiber of ![]() $p$, then
$p$, then ![]() $F_{p}$ does not carry any non-zero pluri-forms either. Hence,
$F_{p}$ does not carry any non-zero pluri-forms either. Hence, 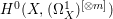 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ is isomorphic to
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ is isomorphic to 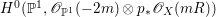 $H^{0}(\mathbb{P}^{1},\mathscr{O}_{\mathbb{P}^{1}}(-2m)\otimes p_{\ast }\mathscr{O}_{X}(mR))$ for
$H^{0}(\mathbb{P}^{1},\mathscr{O}_{\mathbb{P}^{1}}(-2m)\otimes p_{\ast }\mathscr{O}_{X}(mR))$ for ![]() $m>0$, where
$m>0$, where ![]() $R$ is the ramification divisor of
$R$ is the ramification divisor of ![]() $p$. However, since
$p$. However, since  $m(q,b)=1$ for all
$m(q,b)=1$ for all ![]() $b\in B$, we have
$b\in B$, we have  $\sum _{i=1}^{r}[((s_{i}-1)m)/s_{i}]=\sum _{z\in \mathbb{P}^{1}}[((m(p,z)-1)m)/m(p,z)]$ by the definition of
$\sum _{i=1}^{r}[((s_{i}-1)m)/s_{i}]=\sum _{z\in \mathbb{P}^{1}}[((m(p,z)-1)m)/m(p,z)]$ by the definition of ![]() $s_{i}$. Finally, we have
$s_{i}$. Finally, we have 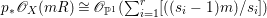 $p_{\ast }\mathscr{O}_{X}(mR)\cong \mathscr{O}_{\mathbb{P}^{1}}(\sum _{i=1}^{r}[((s_{i}-1)m)/s_{i}])$ and
$p_{\ast }\mathscr{O}_{X}(mR)\cong \mathscr{O}_{\mathbb{P}^{1}}(\sum _{i=1}^{r}[((s_{i}-1)m)/s_{i}])$ and 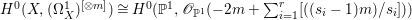 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(\mathbb{P}^{1},\mathscr{O}_{\mathbb{P}^{1}}(-2m+\sum _{i=1}^{r}[((s_{i}-1)m)/s_{i}]))$ by Lemma 3.1.◻
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(\mathbb{P}^{1},\mathscr{O}_{\mathbb{P}^{1}}(-2m+\sum _{i=1}^{r}[((s_{i}-1)m)/s_{i}]))$ by Lemma 3.1.◻
Remark 3.3. Conversely, let 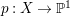 $p:X\rightarrow \mathbb{P}^{1}$ be a fibration such that general fibers of
$p:X\rightarrow \mathbb{P}^{1}$ be a fibration such that general fibers of ![]() $p$ are rationally connected and do not carry non-zero pluri-forms. If
$p$ are rationally connected and do not carry non-zero pluri-forms. If ![]() $X$ carries non-zero pluri-forms, then
$X$ carries non-zero pluri-forms, then ![]() $X$ can be constructed by the method described above. In fact, by the discussion above, we have
$X$ can be constructed by the method described above. In fact, by the discussion above, we have 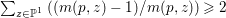 $\sum _{z\in \mathbb{P}^{1}}((m(p,z)-1)/m(p,z))\geqslant 2$. In particular, there are at least three points in
$\sum _{z\in \mathbb{P}^{1}}((m(p,z)-1)/m(p,z))\geqslant 2$. In particular, there are at least three points in ![]() $\mathbb{P}^{1}$ such that the multiplicity of
$\mathbb{P}^{1}$ such that the multiplicity of ![]() $p$ is larger than
$p$ is larger than ![]() $1$ over these points. Let
$1$ over these points. Let 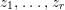 $z_{1},\ldots ,z_{r}$ be all the points in
$z_{1},\ldots ,z_{r}$ be all the points in ![]() $\mathbb{P}^{1}$ such that
$\mathbb{P}^{1}$ such that 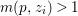 $m(p,z_{i})>1$ for all
$m(p,z_{i})>1$ for all ![]() $i$. Since
$i$. Since ![]() $r\geqslant 3$, there is a smooth curve
$r\geqslant 3$, there is a smooth curve ![]() $B$ and a Galois cover
$B$ and a Galois cover 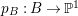 $p_{B}:B\rightarrow \mathbb{P}^{1}$ with Galois group
$p_{B}:B\rightarrow \mathbb{P}^{1}$ with Galois group ![]() $G$ such that
$G$ such that ![]() $p_{B}$ is ramified exactly over the
$p_{B}$ is ramified exactly over the ![]() $z_{i}$ and the degree of ramification is
$z_{i}$ and the degree of ramification is ![]() $m_{i}$ at each point over
$m_{i}$ at each point over ![]() $z_{i}$ (see [Reference Kobayashi and OchiaiKO82, Lemma 6.1]). Let
$z_{i}$ (see [Reference Kobayashi and OchiaiKO82, Lemma 6.1]). Let ![]() $T$ be the normalization of the fiber product
$T$ be the normalization of the fiber product 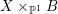 $X\times _{\mathbb{P}^{1}}B$. Then we obtain a natural fibration
$X\times _{\mathbb{P}^{1}}B$. Then we obtain a natural fibration 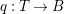 $q:T\rightarrow B$ such that
$q:T\rightarrow B$ such that 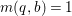 $m(q,b)=1$ for all
$m(q,b)=1$ for all ![]() $b\in B$. Moreover,
$b\in B$. Moreover, ![]() $G$ acts naturally on
$G$ acts naturally on ![]() $T$ and
$T$ and 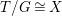 $T/G\cong X$.
$T/G\cong X$.
3.2 The case of threefolds with canonical singularities
If 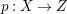 $p:X\rightarrow Z$ is a Mori fibration from a threefold which has
$p:X\rightarrow Z$ is a Mori fibration from a threefold which has ![]() $\mathbb{Q}$-factorial canonical singularities to a smooth curve, then general fibers of
$\mathbb{Q}$-factorial canonical singularities to a smooth curve, then general fibers of ![]() $p$ are Fano surfaces which have canonical singularities. These surfaces do not carry any non-zero pluri-forms by the following theorem.
$p$ are Fano surfaces which have canonical singularities. These surfaces do not carry any non-zero pluri-forms by the following theorem.
Theorem 3.4. If ![]() $S$ is a Fano surface which has canonical singularities, then
$S$ is a Fano surface which has canonical singularities, then 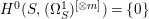 $H^{0}(S,({\rm\Omega}_{S}^{1})^{[\otimes m]})=\{0\}$ for all
$H^{0}(S,({\rm\Omega}_{S}^{1})^{[\otimes m]})=\{0\}$ for all ![]() $m>0$.
$m>0$.
Proof. Assume the opposite. If ![]() $S^{\prime }$ is the result of an MMP for
$S^{\prime }$ is the result of an MMP for ![]() $S$, then
$S$, then ![]() $S^{\prime }$ is a Mori fiber space. By [Reference OuOu14, Theorem 3.1],
$S^{\prime }$ is a Mori fiber space. By [Reference OuOu14, Theorem 3.1], ![]() $S^{\prime }$ has Picard number
$S^{\prime }$ has Picard number ![]() $2$ and we have a Mori fibration
$2$ and we have a Mori fibration 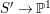 $S^{\prime }\rightarrow \mathbb{P}^{1}$. Let
$S^{\prime }\rightarrow \mathbb{P}^{1}$. Let ![]() $p_{S}$ be the composition of
$p_{S}$ be the composition of 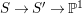 $S\rightarrow S^{\prime }\rightarrow \mathbb{P}^{1}$. By [Reference OuOu14, Theorem 1.5], there is a smooth curve
$S\rightarrow S^{\prime }\rightarrow \mathbb{P}^{1}$. By [Reference OuOu14, Theorem 1.5], there is a smooth curve ![]() $B$ of positive genus and a finite morphism
$B$ of positive genus and a finite morphism ![]() $B\rightarrow \mathbb{P}^{1}$ such that the natural morphism
$B\rightarrow \mathbb{P}^{1}$ such that the natural morphism 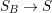 $S_{B}\rightarrow S$ is étale in codimension
$S_{B}\rightarrow S$ is étale in codimension ![]() $1$, where
$1$, where ![]() $S_{B}$ is the normalization of
$S_{B}$ is the normalization of 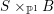 $S\times _{\mathbb{P}^{1}}B$. Hence,
$S\times _{\mathbb{P}^{1}}B$. Hence, ![]() $S_{B}$ is a Fano surface. Moreover, it has canonical singularities (see [Reference Kollár and MoriKM98, Proposition 5.20]). Therefore, it is rationally connected by [Reference Hacon and McKernanHM07, Corollaries 1.3 and 1.5]. Hence,
$S_{B}$ is a Fano surface. Moreover, it has canonical singularities (see [Reference Kollár and MoriKM98, Proposition 5.20]). Therefore, it is rationally connected by [Reference Hacon and McKernanHM07, Corollaries 1.3 and 1.5]. Hence, ![]() $B$ is also rationally connected, which is a contradiction since its genus is positive.◻
$B$ is also rationally connected, which is a contradiction since its genus is positive.◻
Thanks to this theorem, we obtain the following result.
Proposition 3.5. Let ![]() $X$ be a rationally connected threefold which has
$X$ be a rationally connected threefold which has ![]() $\mathbb{Q}$-factorial canonical singularities. Assume that
$\mathbb{Q}$-factorial canonical singularities. Assume that ![]() $X$ carries non-zero pluri-forms. Let
$X$ carries non-zero pluri-forms. Let ![]() $X^{\ast }$ be the result of an MMP for
$X^{\ast }$ be the result of an MMP for ![]() $X$ and assume that there is a Mori fibration
$X$ and assume that there is a Mori fibration 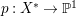 $p:X^{\ast }\rightarrow \mathbb{P}^{1}$. Let
$p:X^{\ast }\rightarrow \mathbb{P}^{1}$. Let ![]() $Y$ be the normalization of the graph of
$Y$ be the normalization of the graph of 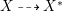 $X{\dashrightarrow}X^{\ast }$. Then
$X{\dashrightarrow}X^{\ast }$. Then ![]() $Y$ can be constructed by the method of Theorem 3.2.
$Y$ can be constructed by the method of Theorem 3.2.
Proof. By Theorem 3.4 and Lemma 2.5, we know that every element in the space 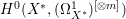 $H^{0}(X^{\ast },({\rm\Omega}_{X^{\ast }}^{1})^{[\otimes m]})$ comes from the base
$H^{0}(X^{\ast },({\rm\Omega}_{X^{\ast }}^{1})^{[\otimes m]})$ comes from the base ![]() $\mathbb{P}^{1}$, and so does every element in
$\mathbb{P}^{1}$, and so does every element in 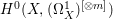 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ by Lemma 2.2. We have a rational map
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ by Lemma 2.2. We have a rational map 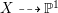 $X{\dashrightarrow}\mathbb{P}^{1}$ induced by
$X{\dashrightarrow}\mathbb{P}^{1}$ induced by ![]() $p$. By Proposition 2.9, we know that
$p$. By Proposition 2.9, we know that 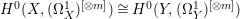 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(Y,({\rm\Omega}_{Y}^{1})^{[\otimes m]})$. Moreover, we have a natural fibration
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(Y,({\rm\Omega}_{Y}^{1})^{[\otimes m]})$. Moreover, we have a natural fibration 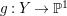 $g:Y\rightarrow \mathbb{P}^{1}$ which is the composition of
$g:Y\rightarrow \mathbb{P}^{1}$ which is the composition of 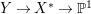 $Y\rightarrow X^{\ast }\rightarrow \mathbb{P}^{1}$. If
$Y\rightarrow X^{\ast }\rightarrow \mathbb{P}^{1}$. If ![]() $F_{g}$ is a general fiber of
$F_{g}$ is a general fiber of ![]() $g$, then there is a birational morphism
$g$, then there is a birational morphism ![]() $F_{g}\rightarrow S$, where
$F_{g}\rightarrow S$, where ![]() $S$ is a general fiber of
$S$ is a general fiber of 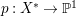 $p:X^{\ast }\rightarrow \mathbb{P}^{1}$. Since
$p:X^{\ast }\rightarrow \mathbb{P}^{1}$. Since ![]() $S$ does not carry any non-zero pluri-forms by Theorem 3.4, neither does
$S$ does not carry any non-zero pluri-forms by Theorem 3.4, neither does ![]() $F_{g}$ by Lemma 2.2. From Remark 3.3, we know that
$F_{g}$ by Lemma 2.2. From Remark 3.3, we know that ![]() $Y$ can be constructed by the method of Theorem 3.2.◻
$Y$ can be constructed by the method of Theorem 3.2.◻
4 Mori fibrations and non-zero pluri-forms
In this section, we study relations between Mori fibrations and non-zero pluri-forms. We consider Mori fibrations from a normal threefold to a normal surface. First, we recall the definition and some properties of slopes. Let ![]() $X$ be a normal projective
$X$ be a normal projective ![]() $\mathbb{Q}$-factorial variety. Let
$\mathbb{Q}$-factorial variety. Let ![]() ${\it\alpha}$ be a class of
${\it\alpha}$ be a class of ![]() $1$-cycles in
$1$-cycles in ![]() $X$. For a coherent sheaf
$X$. For a coherent sheaf ![]() $\mathscr{F}$ of positive rank, we define the slope
$\mathscr{F}$ of positive rank, we define the slope ![]() ${\it\mu}_{{\it\alpha}}(\mathscr{F})$ of
${\it\mu}_{{\it\alpha}}(\mathscr{F})$ of ![]() $\mathscr{F}$ with respect to
$\mathscr{F}$ with respect to ![]() ${\it\alpha}$ by
${\it\alpha}$ by
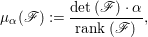 $$\begin{eqnarray}{\it\mu}_{{\it\alpha}}(\mathscr{F}):=\frac{\text{det}\,(\mathscr{F})\cdot {\it\alpha}}{\text{rank}\,(\mathscr{F})},\end{eqnarray}$$
$$\begin{eqnarray}{\it\mu}_{{\it\alpha}}(\mathscr{F}):=\frac{\text{det}\,(\mathscr{F})\cdot {\it\alpha}}{\text{rank}\,(\mathscr{F})},\end{eqnarray}$$ where 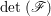 $\text{det}\,(\mathscr{F})$ is the reflexive hull of
$\text{det}\,(\mathscr{F})$ is the reflexive hull of  $\wedge ^{\mathit{rank}\,\mathscr{F}}\mathscr{F}$. A class of movable curves is a class of
$\wedge ^{\mathit{rank}\,\mathscr{F}}\mathscr{F}$. A class of movable curves is a class of ![]() $1$-cycles that has non-negative intersection number with any pseudo-effective divisor. If
$1$-cycles that has non-negative intersection number with any pseudo-effective divisor. If ![]() ${\it\alpha}$ is a class of movable curves, then
${\it\alpha}$ is a class of movable curves, then 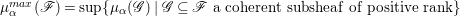 ${\it\mu}_{{\it\alpha}}^{max}(\mathscr{F})=\text{sup}\{{\it\mu}_{{\it\alpha}}(\mathscr{G})\mid \mathscr{G}\subseteq \mathscr{F}~\text{a coherent subsheaf of positive rank}\}$ is well defined. For any coherent sheaf
${\it\mu}_{{\it\alpha}}^{max}(\mathscr{F})=\text{sup}\{{\it\mu}_{{\it\alpha}}(\mathscr{G})\mid \mathscr{G}\subseteq \mathscr{F}~\text{a coherent subsheaf of positive rank}\}$ is well defined. For any coherent sheaf ![]() $\mathscr{F}$, there is a saturated coherent subsheaf
$\mathscr{F}$, there is a saturated coherent subsheaf ![]() $\mathscr{G}\subseteq \mathscr{F}$ such that
$\mathscr{G}\subseteq \mathscr{F}$ such that 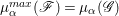 ${\it\mu}_{{\it\alpha}}^{max}(\mathscr{F})={\it\mu}_{{\it\alpha}}(\mathscr{G})$. If
${\it\mu}_{{\it\alpha}}^{max}(\mathscr{F})={\it\mu}_{{\it\alpha}}(\mathscr{G})$. If ![]() $\mathscr{E}$ and
$\mathscr{E}$ and ![]() $\mathscr{F}$ are two coherent sheaves of positive rank, then
$\mathscr{F}$ are two coherent sheaves of positive rank, then 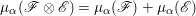 ${\it\mu}_{{\it\alpha}}(\mathscr{F}\otimes \mathscr{E})={\it\mu}_{{\it\alpha}}(\mathscr{F})+{\it\mu}_{{\it\alpha}}(\mathscr{E})$. For more detail, see [Reference Greb, Kebekus and PeternellGKP14, Appendix A]
${\it\mu}_{{\it\alpha}}(\mathscr{F}\otimes \mathscr{E})={\it\mu}_{{\it\alpha}}(\mathscr{F})+{\it\mu}_{{\it\alpha}}(\mathscr{E})$. For more detail, see [Reference Greb, Kebekus and PeternellGKP14, Appendix A]
4.1 General properties
Consider a Mori fibration 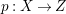 $p:X\rightarrow Z$ from a normal rationally connected threefold to a normal variety
$p:X\rightarrow Z$ from a normal rationally connected threefold to a normal variety ![]() $Z$ of positive dimension. Assume that
$Z$ of positive dimension. Assume that ![]() $X$ has
$X$ has ![]() $\mathbb{Q}$-factorial klt singularities. Let
$\mathbb{Q}$-factorial klt singularities. Let 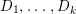 $D_{1},\ldots ,D_{k}$ be all prime Weil divisors in
$D_{1},\ldots ,D_{k}$ be all prime Weil divisors in ![]() $Z$ such that
$Z$ such that 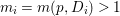 $m_{i}=m(p,D_{i})>1$. Let
$m_{i}=m(p,D_{i})>1$. Let 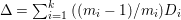 ${\rm\Delta}=\sum _{i=1}^{k}((m_{i}-1)/m_{i})D_{i}$. Then
${\rm\Delta}=\sum _{i=1}^{k}((m_{i}-1)/m_{i})D_{i}$. Then 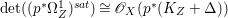 $\text{det}((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})\cong \mathscr{O}_{X}(p^{\ast }(K_{Z}+{\rm\Delta}))$ (see Remark 4.5). Assume that
$\text{det}((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})\cong \mathscr{O}_{X}(p^{\ast }(K_{Z}+{\rm\Delta}))$ (see Remark 4.5). Assume that ![]() $X$ carries non-zero pluri-forms and general fibers of
$X$ carries non-zero pluri-forms and general fibers of ![]() $p$ do not carry any non-zero pluri-forms. If
$p$ do not carry any non-zero pluri-forms. If 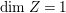 $\text{dim}\,Z=1$, then
$\text{dim}\,Z=1$, then 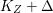 $K_{Z}+{\rm\Delta}$ is an effective
$K_{Z}+{\rm\Delta}$ is an effective ![]() $\mathbb{Q}$-divisor of degree
$\mathbb{Q}$-divisor of degree 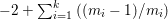 $-2+\sum _{i=1}^{k}((m_{i}-1)/m_{i})$ on
$-2+\sum _{i=1}^{k}((m_{i}-1)/m_{i})$ on ![]() $\mathbb{P}^{1}$ (see Section 3). The aim of this subsection is to prove something analogous in the case when
$\mathbb{P}^{1}$ (see Section 3). The aim of this subsection is to prove something analogous in the case when 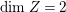 $\text{dim}\,Z=2$. We prove that if
$\text{dim}\,Z=2$. We prove that if 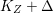 $K_{Z}+{\rm\Delta}$ is not pseudo-effective, then there will be a fibration from
$K_{Z}+{\rm\Delta}$ is not pseudo-effective, then there will be a fibration from ![]() $Z$ to
$Z$ to ![]() $\mathbb{P}^{1}$. In this case, we have an induced fibration
$\mathbb{P}^{1}$. In this case, we have an induced fibration 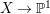 $X\rightarrow \mathbb{P}^{1}$ and we are in the same situation as in Section 3 (see Lemma 4.10). In order to do this, we run an MMP for the pair
$X\rightarrow \mathbb{P}^{1}$ and we are in the same situation as in Section 3 (see Lemma 4.10). In order to do this, we run an MMP for the pair ![]() $(Z,{\rm\Delta})$. To this end, we prove the following proposition which implies that the pair
$(Z,{\rm\Delta})$. To this end, we prove the following proposition which implies that the pair ![]() $(Z,{\rm\Delta})$ is klt.
$(Z,{\rm\Delta})$ is klt.
Proposition 4.1. Let 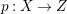 $p:X\rightarrow Z$ be a Mori fibration from a
$p:X\rightarrow Z$ be a Mori fibration from a ![]() $\mathbb{Q}$-factorial klt quasi-projective variety
$\mathbb{Q}$-factorial klt quasi-projective variety ![]() $X$ to a normal variety
$X$ to a normal variety ![]() $Z$. Let
$Z$. Let 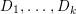 $D_{1},\ldots ,D_{k}$ be pairwise distinct prime Weil divisors in
$D_{1},\ldots ,D_{k}$ be pairwise distinct prime Weil divisors in ![]() $Z$ such that
$Z$ such that 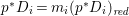 $p^{\ast }D_{i}=m_{i}(p^{\ast }D_{i})_{\mathit{red}}$ with
$p^{\ast }D_{i}=m_{i}(p^{\ast }D_{i})_{\mathit{red}}$ with ![]() $m_{i}\geqslant 2$. Then the pair
$m_{i}\geqslant 2$. Then the pair 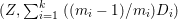 $(Z,\sum _{i=1}^{k}((m_{i}-1)/m_{i})D_{i})$ is klt.
$(Z,\sum _{i=1}^{k}((m_{i}-1)/m_{i})D_{i})$ is klt.
Proof. Let  $D=D_{1}+\cdots +D_{k}$. By [Reference Kawamata, Matsuda and MatsukiKMM87, Lemma 5-1-5],
$D=D_{1}+\cdots +D_{k}$. By [Reference Kawamata, Matsuda and MatsukiKMM87, Lemma 5-1-5], ![]() $Z$ is
$Z$ is ![]() $\mathbb{Q}$-factorial. Note that the problem is local in
$\mathbb{Q}$-factorial. Note that the problem is local in ![]() $Z$, and we may assume that
$Z$, and we may assume that ![]() $Z$ is affine.
$Z$ is affine.
We construct by induction a finite morphism  $c_{k}:Z_{k}\rightarrow Z$ which is ramified over
$c_{k}:Z_{k}\rightarrow Z$ which is ramified over ![]() $D$ such that
$D$ such that 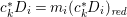 $c_{k}^{\ast }D_{i}=m_{i}(c_{k}^{\ast }D_{i})_{\mathit{red}}$ for all
$c_{k}^{\ast }D_{i}=m_{i}(c_{k}^{\ast }D_{i})_{\mathit{red}}$ for all ![]() $i$. Let
$i$. Let ![]() $k_{1}$ be the smallest positive integer such that
$k_{1}$ be the smallest positive integer such that ![]() $k_{1}D_{1}$ is a Cartier divisor. By taking the
$k_{1}D_{1}$ is a Cartier divisor. By taking the ![]() $k_{1}$th root of the function defining the Cartier divisor
$k_{1}$th root of the function defining the Cartier divisor ![]() $k_{1}D_{1}$, we can construct a finite morphism
$k_{1}D_{1}$, we can construct a finite morphism 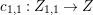 $c_{1,1}:Z_{1,1}\rightarrow Z$ which is étale in codimension
$c_{1,1}:Z_{1,1}\rightarrow Z$ which is étale in codimension ![]() $1$. Moreover,
$1$. Moreover, ![]() $c_{1,1}^{\ast }D_{1}$ is a reduced Cartier divisor (see [Reference MoriMor88, Proposition-Definition 1.11]). By taking the
$c_{1,1}^{\ast }D_{1}$ is a reduced Cartier divisor (see [Reference MoriMor88, Proposition-Definition 1.11]). By taking the ![]() $m_{1}$th root of the function defining the Cartier divisor
$m_{1}$th root of the function defining the Cartier divisor ![]() $c_{1,1}^{\ast }D_{1}$, we can find a finite morphism
$c_{1,1}^{\ast }D_{1}$, we can find a finite morphism 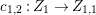 $c_{1,2}:Z_{1}\rightarrow Z_{1,1}$ which is ramified exactly over
$c_{1,2}:Z_{1}\rightarrow Z_{1,1}$ which is ramified exactly over ![]() $D_{1}$ with ramification degree
$D_{1}$ with ramification degree ![]() $m_{1}$ (see [Reference LazarsfeldLaz04, Section 4.1B]). Let
$m_{1}$ (see [Reference LazarsfeldLaz04, Section 4.1B]). Let 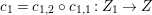 $c_{1}=c_{1,2}\circ c_{1,1}:Z_{1}\rightarrow Z$. Then
$c_{1}=c_{1,2}\circ c_{1,1}:Z_{1}\rightarrow Z$. Then 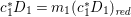 $c_{1}^{\ast }D_{1}=m_{1}(c_{1}^{\ast }D_{1})_{\mathit{red}}$. Assume that we have constructed a finite morphism
$c_{1}^{\ast }D_{1}=m_{1}(c_{1}^{\ast }D_{1})_{\mathit{red}}$. Assume that we have constructed a finite morphism 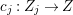 $c_{j}:Z_{j}\rightarrow Z$ such that
$c_{j}:Z_{j}\rightarrow Z$ such that 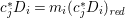 $c_{j}^{\ast }D_{i}=m_{i}(c_{j}^{\ast }D_{i})_{\mathit{red}}$ for any
$c_{j}^{\ast }D_{i}=m_{i}(c_{j}^{\ast }D_{i})_{\mathit{red}}$ for any 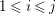 $1\leqslant i\leqslant j$ and
$1\leqslant i\leqslant j$ and ![]() $c_{j}^{\ast }D_{i}$ is reduced for any
$c_{j}^{\ast }D_{i}$ is reduced for any ![]() $i>j$, where
$i>j$, where 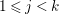 $1\leqslant j<k$. Let
$1\leqslant j<k$. Let 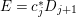 $E=c_{j}^{\ast }D_{j+1}$. Then
$E=c_{j}^{\ast }D_{j+1}$. Then ![]() $E$ is a reduced divisor. By the same method as above, we can construct a finite morphism
$E$ is a reduced divisor. By the same method as above, we can construct a finite morphism 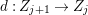 $d:Z_{j+1}\rightarrow Z_{j}$ which is ramified exactly over
$d:Z_{j+1}\rightarrow Z_{j}$ which is ramified exactly over ![]() $E$ with ramification degree
$E$ with ramification degree ![]() $m_{j+1}$. Let
$m_{j+1}$. Let 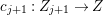 $c_{j+1}:Z_{j+1}\rightarrow Z$ be the composition
$c_{j+1}:Z_{j+1}\rightarrow Z$ be the composition ![]() $c_{j}\circ d$. Then
$c_{j}\circ d$. Then 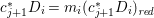 $c_{j+1}^{\ast }D_{i}=m_{i}(c_{j+1}^{\ast }D_{i})_{\mathit{red}}$ for any
$c_{j+1}^{\ast }D_{i}=m_{i}(c_{j+1}^{\ast }D_{i})_{\mathit{red}}$ for any 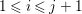 $1\leqslant i\leqslant j+1$ and
$1\leqslant i\leqslant j+1$ and ![]() $c_{j+1}^{\ast }D_{i}$ is reduced for any
$c_{j+1}^{\ast }D_{i}$ is reduced for any 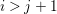 $i>j+1$. By induction, we can construct the finite morphism
$i>j+1$. By induction, we can construct the finite morphism ![]() $c_{k}$.
$c_{k}$.
We have 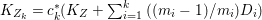 $K_{Z_{k}}=c_{k}^{\ast }(K_{Z}+\sum _{i=1}^{k}((m_{i}-1)/m_{i})D_{i})$. Let
$K_{Z_{k}}=c_{k}^{\ast }(K_{Z}+\sum _{i=1}^{k}((m_{i}-1)/m_{i})D_{i})$. Let ![]() $X_{k}$ be the normalization of
$X_{k}$ be the normalization of 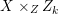 $X\times _{Z}Z_{k}$. Then the natural projection
$X\times _{Z}Z_{k}$. Then the natural projection 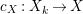 $c_{X}:X_{k}\rightarrow X$ is étale in codimension 1 and
$c_{X}:X_{k}\rightarrow X$ is étale in codimension 1 and 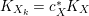 $K_{X_{k}}=c_{X}^{\ast }K_{X}$. Hence,
$K_{X_{k}}=c_{X}^{\ast }K_{X}$. Hence, ![]() $X_{k}$ is klt by [Reference Kollár and MoriKM98, Proposition 5.20]. Moreover,
$X_{k}$ is klt by [Reference Kollár and MoriKM98, Proposition 5.20]. Moreover, 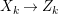 $X_{k}\rightarrow Z_{k}$ is a Fano fibration since
$X_{k}\rightarrow Z_{k}$ is a Fano fibration since ![]() $X\rightarrow Z$ is a Mori fibration. Hence, there is a
$X\rightarrow Z$ is a Mori fibration. Hence, there is a ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() ${\rm\Delta}_{k}$ such that the pair
${\rm\Delta}_{k}$ such that the pair 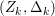 $(Z_{k},{\rm\Delta}_{k})$ is klt by [Reference FujinoFuj99, Corollary 4.7]. Since
$(Z_{k},{\rm\Delta}_{k})$ is klt by [Reference FujinoFuj99, Corollary 4.7]. Since ![]() $K_{Z_{k}}$ is
$K_{Z_{k}}$ is ![]() $\mathbb{Q}$-Cartier,
$\mathbb{Q}$-Cartier, ![]() $Z_{k}$ is klt (see [Reference Kollár and MoriKM98, Corollary 2.35]). Therefore, the pair
$Z_{k}$ is klt (see [Reference Kollár and MoriKM98, Corollary 2.35]). Therefore, the pair 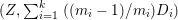 $(Z,\sum _{i=1}^{k}((m_{i}-1)/m_{i})D_{i})$ is also klt by [Reference Kollár and MoriKM98, Proposition 5.20].◻
$(Z,\sum _{i=1}^{k}((m_{i}-1)/m_{i})D_{i})$ is also klt by [Reference Kollár and MoriKM98, Proposition 5.20].◻
In the remainder of this subsection, our aim is to prove the following theorem.
Theorem 4.2. Let 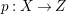 $p:X\rightarrow Z$ be a Mori fibration from a projective normal threefold to a normal projective surface. Assume that
$p:X\rightarrow Z$ be a Mori fibration from a projective normal threefold to a normal projective surface. Assume that ![]() $X$ has
$X$ has ![]() $\mathbb{Q}$-factorial klt singularities. Let
$\mathbb{Q}$-factorial klt singularities. Let 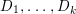 $D_{1},\ldots ,D_{k}$ be all prime Weil divisors in
$D_{1},\ldots ,D_{k}$ be all prime Weil divisors in ![]() $Z$ such that
$Z$ such that 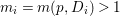 $m_{i}=m(p,D_{i})>1$. Let
$m_{i}=m(p,D_{i})>1$. Let 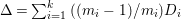 ${\rm\Delta}=\sum _{i=1}^{k}((m_{i}-1)/m_{i})D_{i}$. If
${\rm\Delta}=\sum _{i=1}^{k}((m_{i}-1)/m_{i})D_{i}$. If ![]() $X$ carries non-zero pluri-forms and
$X$ carries non-zero pluri-forms and 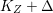 $K_{Z}+{\rm\Delta}$ is not pseudo-effective, then the result
$K_{Z}+{\rm\Delta}$ is not pseudo-effective, then the result ![]() $Z^{\prime }$ of any MMP for the pair
$Z^{\prime }$ of any MMP for the pair ![]() $(Z,{\rm\Delta})$ has Picard number
$(Z,{\rm\Delta})$ has Picard number ![]() $2$.
$2$.
First, we would like to illustrate the idea of the proof in a simple case. Let 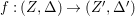 $f:(Z,{\rm\Delta})\rightarrow (Z^{\prime },{\rm\Delta}^{\prime })$ be the result of an MMP for the pair
$f:(Z,{\rm\Delta})\rightarrow (Z^{\prime },{\rm\Delta}^{\prime })$ be the result of an MMP for the pair ![]() $(Z,{\rm\Delta})$. Assume in a first stage that
$(Z,{\rm\Delta})$. Assume in a first stage that ![]() $Z=Z^{\prime }$. We argue by contradiction. Assume that
$Z=Z^{\prime }$. We argue by contradiction. Assume that ![]() $Z^{\prime }$ has Picard number
$Z^{\prime }$ has Picard number ![]() $1$. Since general fibers of
$1$. Since general fibers of ![]() $p$ are isomorphic to
$p$ are isomorphic to ![]() $\mathbb{P}^{1}$, they do not carry any non-zero pluri-forms. By Lemma 2.5, the non-zero pluri-forms of
$\mathbb{P}^{1}$, they do not carry any non-zero pluri-forms. By Lemma 2.5, the non-zero pluri-forms of ![]() $X$ come from
$X$ come from 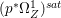 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$. Since
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$. Since 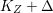 $K_{Z}+{\rm\Delta}$ is not pseudo-effective, we can prove that there is a rank-
$K_{Z}+{\rm\Delta}$ is not pseudo-effective, we can prove that there is a rank-![]() $1$ coherent subsheaf
$1$ coherent subsheaf ![]() $\mathscr{H}$ of
$\mathscr{H}$ of 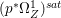 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ such that
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ such that ![]() $\mathscr{H}^{[\otimes l]}$ is an invertible sheaf which has non-zero global sections for some positive integer
$\mathscr{H}^{[\otimes l]}$ is an invertible sheaf which has non-zero global sections for some positive integer ![]() $l$. Next, we can prove that
$l$. Next, we can prove that ![]() $\mathscr{H}^{[\otimes l]}$ is isomorphic to
$\mathscr{H}^{[\otimes l]}$ is isomorphic to ![]() $\mathscr{O}_{X}$ under the assumption that
$\mathscr{O}_{X}$ under the assumption that ![]() $Z$ has Picard number
$Z$ has Picard number ![]() $1$ (by using Lemma 4.8). Let
$1$ (by using Lemma 4.8). Let 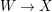 $W\rightarrow X$ be the normalization of the cyclic cover with respect to the isomorphism
$W\rightarrow X$ be the normalization of the cyclic cover with respect to the isomorphism 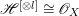 $\mathscr{H}^{[\otimes l]}\cong \mathscr{O}_{X}$ (see [Reference Kollár and MoriKM98, Definition 2.52]). Let
$\mathscr{H}^{[\otimes l]}\cong \mathscr{O}_{X}$ (see [Reference Kollár and MoriKM98, Definition 2.52]). Let 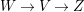 $W\rightarrow V\rightarrow Z$ be the Stein factorization, then
$W\rightarrow V\rightarrow Z$ be the Stein factorization, then ![]() $V$ will be a klt Fano variety (by Lemma 4.7). Moreover,
$V$ will be a klt Fano variety (by Lemma 4.7). Moreover, 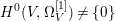 $H^{0}(V,{\rm\Omega}_{V}^{[1]})\neq \{0\}$ (we use Lemma 4.9). This contradicts [Reference Greb, Kebekus, Kovács and PeternellGKKP11, Theorem 5.1].
$H^{0}(V,{\rm\Omega}_{V}^{[1]})\neq \{0\}$ (we use Lemma 4.9). This contradicts [Reference Greb, Kebekus, Kovács and PeternellGKKP11, Theorem 5.1].
However, in general, ![]() $Z^{\prime }$ is different from
$Z^{\prime }$ is different from ![]() $Z$ and the fibration
$Z$ and the fibration 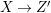 $X\rightarrow Z^{\prime }$ is not equidimensional. The idea of the proof is the same as above but the details are more complicated. We work over an open subset
$X\rightarrow Z^{\prime }$ is not equidimensional. The idea of the proof is the same as above but the details are more complicated. We work over an open subset ![]() $Z_{0}$ of
$Z_{0}$ of ![]() $Z$ such that
$Z$ such that ![]() $f|_{Z_{0}}$ is an isomorphism and
$f|_{Z_{0}}$ is an isomorphism and 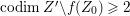 $\text{codim}\,Z^{\prime }\setminus f(Z_{0})\geqslant 2$. For the complete proof of the theorem, we need several lemmas.
$\text{codim}\,Z^{\prime }\setminus f(Z_{0})\geqslant 2$. For the complete proof of the theorem, we need several lemmas.
Lemma 4.3. Let 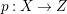 $p:X\rightarrow Z$ be an equidimensional morphism between smooth varieties. Let
$p:X\rightarrow Z$ be an equidimensional morphism between smooth varieties. Let ![]() $n$ be the dimension of
$n$ be the dimension of ![]() $X$, and let
$X$, and let ![]() $d$ be the dimension of
$d$ be the dimension of ![]() $Z$. Let
$Z$. Let ![]() $D$ be a prime divisor in
$D$ be a prime divisor in ![]() $Z$, and let
$Z$, and let ![]() $E$ be a prime divisor in
$E$ be a prime divisor in ![]() $X$ such that
$X$ such that ![]() $E$ is a component of
$E$ is a component of ![]() $p^{\ast }D$. Assume that the coefficient of
$p^{\ast }D$. Assume that the coefficient of ![]() $E$ in
$E$ in ![]() $p^{\ast }D$ is
$p^{\ast }D$ is ![]() $k$. Then for any general point
$k$. Then for any general point ![]() $x\in E$, there is an open neighborhood
$x\in E$, there is an open neighborhood ![]() $U\subseteq X$ of
$U\subseteq X$ of ![]() $x$ such that
$x$ such that 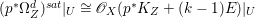 $(p^{\ast }{\rm\Omega}_{Z}^{d})^{sat}|_{U}\cong \mathscr{O}_{X}(p^{\ast }K_{Z}+(k-1)E)|_{U}$, where
$(p^{\ast }{\rm\Omega}_{Z}^{d})^{sat}|_{U}\cong \mathscr{O}_{X}(p^{\ast }K_{Z}+(k-1)E)|_{U}$, where 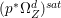 $(p^{\ast }{\rm\Omega}_{Z}^{d})^{sat}$ is the saturation of
$(p^{\ast }{\rm\Omega}_{Z}^{d})^{sat}$ is the saturation of ![]() $p^{\ast }{\rm\Omega}_{Z}^{d}$ in
$p^{\ast }{\rm\Omega}_{Z}^{d}$ in ![]() ${\rm\Omega}_{X}^{d}$.
${\rm\Omega}_{X}^{d}$.
Proof. We may assume that ![]() $E$ is smooth around
$E$ is smooth around ![]() $x$ and
$x$ and ![]() $D$ is smooth around
$D$ is smooth around ![]() $p(x)$. There exist local coordinates
$p(x)$. There exist local coordinates 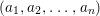 $(a_{1},a_{2},\ldots ,a_{n})$ and
$(a_{1},a_{2},\ldots ,a_{n})$ and 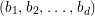 $(b_{1},b_{2},\ldots ,b_{d})$ of
$(b_{1},b_{2},\ldots ,b_{d})$ of ![]() $X$ and
$X$ and ![]() $Z$ around
$Z$ around ![]() $x$ and
$x$ and ![]() $p(x)$ such that
$p(x)$ such that ![]() $E$ is defined by
$E$ is defined by  $\{a_{1}=0\}$,
$\{a_{1}=0\}$, ![]() $D$ is defined by
$D$ is defined by  $\{b_{1}=0\}$ and
$\{b_{1}=0\}$ and ![]() $p$ is given by
$p$ is given by 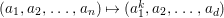 $(a_{1},a_{2},\ldots ,a_{n})\mapsto (a_{1}^{k},a_{2},\ldots ,a_{d})$. With these coordinates, the natural morphism
$(a_{1},a_{2},\ldots ,a_{n})\mapsto (a_{1}^{k},a_{2},\ldots ,a_{d})$. With these coordinates, the natural morphism 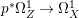 $p^{\ast }{\rm\Omega}_{Z}^{1}\rightarrow {\rm\Omega}_{X}^{1}$ is given by
$p^{\ast }{\rm\Omega}_{Z}^{1}\rightarrow {\rm\Omega}_{X}^{1}$ is given by
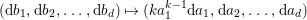 $$\begin{eqnarray}(\text{d}b_{1},\text{d}b_{2},\ldots ,\text{d}b_{d})\mapsto (ka_{1}^{k-1}\text{d}a_{1},\text{d}a_{2},\ldots ,\text{d}a_{d})\end{eqnarray}$$
$$\begin{eqnarray}(\text{d}b_{1},\text{d}b_{2},\ldots ,\text{d}b_{d})\mapsto (ka_{1}^{k-1}\text{d}a_{1},\text{d}a_{2},\ldots ,\text{d}a_{d})\end{eqnarray}$$ and the image of the natural morphism 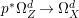 $p^{\ast }{\rm\Omega}_{Z}^{d}\rightarrow {\rm\Omega}_{X}^{d}$ is generated by
$p^{\ast }{\rm\Omega}_{Z}^{d}\rightarrow {\rm\Omega}_{X}^{d}$ is generated by 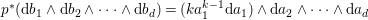 $p^{\ast }(\text{d}b_{1}\wedge \text{d}b_{2}\wedge \cdots \wedge \text{d}b_{d})=(ka_{1}^{k-1}\text{d}a_{1})\wedge \text{d}a_{2}\wedge \cdots \wedge \text{d}a_{d}$. Hence,
$p^{\ast }(\text{d}b_{1}\wedge \text{d}b_{2}\wedge \cdots \wedge \text{d}b_{d})=(ka_{1}^{k-1}\text{d}a_{1})\wedge \text{d}a_{2}\wedge \cdots \wedge \text{d}a_{d}$. Hence, 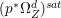 $(p^{\ast }{\rm\Omega}_{Z}^{d})^{sat}$ is generated by
$(p^{\ast }{\rm\Omega}_{Z}^{d})^{sat}$ is generated by 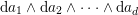 $\text{d}a_{1}\wedge \text{d}a_{2}\wedge \cdots \wedge \text{d}a_{d}$. Since
$\text{d}a_{1}\wedge \text{d}a_{2}\wedge \cdots \wedge \text{d}a_{d}$. Since  $\{a_{1}=0\}$ defines the divisor
$\{a_{1}=0\}$ defines the divisor ![]() $E$, we have
$E$, we have 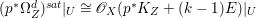 $(p^{\ast }{\rm\Omega}_{Z}^{d})^{sat}|_{U}\cong \mathscr{O}_{X}(p^{\ast }K_{Z}+(k-1)E)|_{U}$ for some open neighborhood
$(p^{\ast }{\rm\Omega}_{Z}^{d})^{sat}|_{U}\cong \mathscr{O}_{X}(p^{\ast }K_{Z}+(k-1)E)|_{U}$ for some open neighborhood ![]() $U$ of
$U$ of ![]() $x$.◻
$x$.◻
Lemma 4.4. Let 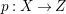 $p:X\rightarrow Z$ be an equidimensional morphism between normal varieties. Assume that
$p:X\rightarrow Z$ be an equidimensional morphism between normal varieties. Assume that ![]() $Z$ is
$Z$ is ![]() $\mathbb{Q}$-factorial. Let
$\mathbb{Q}$-factorial. Let  $D_{1},\ldots ,D_{r}$ be all the prime divisors in
$D_{1},\ldots ,D_{r}$ be all the prime divisors in ![]() $Z$ such that
$Z$ such that 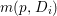 $m(p,D_{i})$ is larger than
$m(p,D_{i})$ is larger than ![]() $1$. Write
$1$. Write 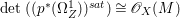 $\text{det}\,((p^{\ast }({\rm\Omega}_{Z}^{1}))^{sat})\cong \mathscr{O}_{X}(M)$, where
$\text{det}\,((p^{\ast }({\rm\Omega}_{Z}^{1}))^{sat})\cong \mathscr{O}_{X}(M)$, where ![]() $M$ is a divisor on
$M$ is a divisor on ![]() $X$. Then
$X$. Then 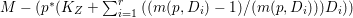 $M-(p^{\ast }(K_{Z}+\sum _{i=1}^{r}((m(p,D_{i})-1)/(m(p,D_{i})))D_{i}))$ is
$M-(p^{\ast }(K_{Z}+\sum _{i=1}^{r}((m(p,D_{i})-1)/(m(p,D_{i})))D_{i}))$ is ![]() $\mathbb{Q}$-effective.
$\mathbb{Q}$-effective.
Proof. By Proposition 2.1, we only have to prove the assertion on an open subset of ![]() $X$ whose complement is of codimension at least
$X$ whose complement is of codimension at least ![]() $2$. Hence, we may assume that both
$2$. Hence, we may assume that both ![]() $X$ and
$X$ and ![]() $Z$ are smooth and that
$Z$ are smooth and that 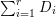 $\sum _{i=1}^{r}D_{i}$ is smooth. In this case, by Lemma 4.3, the divisor
$\sum _{i=1}^{r}D_{i}$ is smooth. In this case, by Lemma 4.3, the divisor ![]() $M$ is linearly equivalent to
$M$ is linearly equivalent to 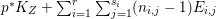 $p^{\ast }K_{Z}+\sum _{i=1}^{r}\sum _{j=1}^{s_{i}}(n_{i,j}-1)E_{i,j}$, where the
$p^{\ast }K_{Z}+\sum _{i=1}^{r}\sum _{j=1}^{s_{i}}(n_{i,j}-1)E_{i,j}$, where the 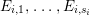 $E_{i,1},\ldots ,E_{i,s_{i}}$ are the components of
$E_{i,1},\ldots ,E_{i,s_{i}}$ are the components of ![]() $p^{\ast }D_{i}$ and
$p^{\ast }D_{i}$ and ![]() $n_{i,j}$ is the coefficient of
$n_{i,j}$ is the coefficient of ![]() $E_{i,j}$ in
$E_{i,j}$ in ![]() $p^{\ast }D_{i}$. Since
$p^{\ast }D_{i}$. Since 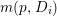 $m(p,D_{i})$ is the smallest integer among
$m(p,D_{i})$ is the smallest integer among 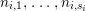 $n_{i,1},\ldots ,n_{i,s_{i}}$, we have
$n_{i,1},\ldots ,n_{i,s_{i}}$, we have 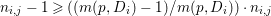 $n_{i,j}-1\geqslant ((m(p,D_{i})-1)/m(p,D_{i}))\cdot n_{i,j}$. Thus,
$n_{i,j}-1\geqslant ((m(p,D_{i})-1)/m(p,D_{i}))\cdot n_{i,j}$. Thus,
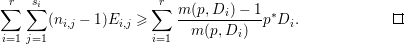 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{s_{i}}(n_{i,j}-1)E_{i,j}\geqslant \mathop{\sum }_{i=1}^{r}\frac{m(p,D_{i})-1}{m(p,D_{i})}p^{\ast }D_{i}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{s_{i}}(n_{i,j}-1)E_{i,j}\geqslant \mathop{\sum }_{i=1}^{r}\frac{m(p,D_{i})-1}{m(p,D_{i})}p^{\ast }D_{i}.\end{eqnarray}$$Remark 4.5. With the notation above, if in addition ![]() $p$ is a Mori fibration, then
$p$ is a Mori fibration, then ![]() $p^{\ast }D_{i}$ is irreducible for all
$p^{\ast }D_{i}$ is irreducible for all ![]() $i$ since
$i$ since ![]() $p$ has relative Picard number 1. In this case we obtain that
$p$ has relative Picard number 1. In this case we obtain that
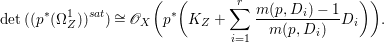 $$\begin{eqnarray}\text{det}\,((p^{\ast }({\rm\Omega}_{Z}^{1}))^{sat})\cong \mathscr{O}_{X}\biggl(p^{\ast }\biggl(K_{Z}+\mathop{\sum }_{i=1}^{r}\frac{m(p,D_{i})-1}{m(p,D_{i})}D_{i}\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\text{det}\,((p^{\ast }({\rm\Omega}_{Z}^{1}))^{sat})\cong \mathscr{O}_{X}\biggl(p^{\ast }\biggl(K_{Z}+\mathop{\sum }_{i=1}^{r}\frac{m(p,D_{i})-1}{m(p,D_{i})}D_{i}\biggr)\biggr).\end{eqnarray}$$Lemma 4.6. Let 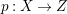 $p:X\rightarrow Z$ be an equidimensional fibration between normal varieties. Let
$p:X\rightarrow Z$ be an equidimensional fibration between normal varieties. Let 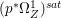 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ be the saturation of the image of
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ be the saturation of the image of ![]() $p^{\ast }{\rm\Omega}_{Z}^{1}$ in
$p^{\ast }{\rm\Omega}_{Z}^{1}$ in ![]() ${\rm\Omega}_{X}^{[1]}$. Then
${\rm\Omega}_{X}^{[1]}$. Then 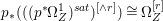 $p_{\ast }(((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\wedge r]})\cong {\rm\Omega}_{Z}^{[r]}$ for
$p_{\ast }(((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\wedge r]})\cong {\rm\Omega}_{Z}^{[r]}$ for ![]() $r>0$.
$r>0$.
Proof. Let ![]() $D$ be the sum of the divisors in
$D$ be the sum of the divisors in ![]() $Z$ over which
$Z$ over which ![]() $p$ does not have reduced fibers. Applying Proposition 2.1 several times, we can suppose without loss of generality that
$p$ does not have reduced fibers. Applying Proposition 2.1 several times, we can suppose without loss of generality that ![]() $Z$ is smooth and
$Z$ is smooth and ![]() $D$ is a simple normal crossing divisor. Let
$D$ is a simple normal crossing divisor. Let 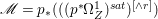 $\mathscr{M}=p_{\ast }(((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\wedge r]})$.
$\mathscr{M}=p_{\ast }(((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\wedge r]})$.
First, we prove that there is a natural injection from ![]() ${\rm\Omega}_{Z}^{r}$ to
${\rm\Omega}_{Z}^{r}$ to ![]() $\mathscr{M}$. We have an injection from
$\mathscr{M}$. We have an injection from ![]() $p^{\ast }{\rm\Omega}_{Z}^{1}$ to
$p^{\ast }{\rm\Omega}_{Z}^{1}$ to 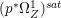 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$. Hence, the natural morphism from
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$. Hence, the natural morphism from 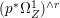 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{\wedge r}$ to
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{\wedge r}$ to 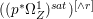 $((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\wedge r]}$ is generically injective. Since
$((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\wedge r]}$ is generically injective. Since 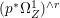 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{\wedge r}$ is without torsion, the natural morphism from
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{\wedge r}$ is without torsion, the natural morphism from 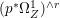 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{\wedge r}$ to
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{\wedge r}$ to 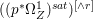 $((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\wedge r]}$ is injective. Since
$((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\wedge r]}$ is injective. Since 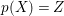 $p(X)=Z$, we have an injection from
$p(X)=Z$, we have an injection from 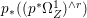 $p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{\wedge r})$ to
$p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{\wedge r})$ to ![]() $\mathscr{M}$. By the projection formula, this implies that
$\mathscr{M}$. By the projection formula, this implies that ![]() ${\rm\Omega}_{Z}^{r}$ is a subsheaf of
${\rm\Omega}_{Z}^{r}$ is a subsheaf of ![]() $\mathscr{M}$.
$\mathscr{M}$.
Now we prove that  ${\rm\Omega}_{Z}^{r}\cong \mathscr{M}$. Let
${\rm\Omega}_{Z}^{r}\cong \mathscr{M}$. Let 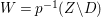 $W=p^{-1}(Z\setminus D)$. Then the morphism
$W=p^{-1}(Z\setminus D)$. Then the morphism 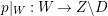 $p|_{W}:W\rightarrow Z\setminus D$ is smooth in codimension
$p|_{W}:W\rightarrow Z\setminus D$ is smooth in codimension ![]() $1$. Thus,
$1$. Thus,
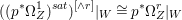 $$\begin{eqnarray}((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\wedge r]}|_{W}\cong p^{\ast }{\rm\Omega}_{Z}^{r}|_{W}\end{eqnarray}$$
$$\begin{eqnarray}((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\wedge r]}|_{W}\cong p^{\ast }{\rm\Omega}_{Z}^{r}|_{W}\end{eqnarray}$$ (see the proof of Lemma 4.3). Then we obtain 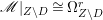 $\mathscr{M}|_{Z\setminus D}\cong {\rm\Omega}_{Z\setminus D}^{r}$ by the projection formula. Let
$\mathscr{M}|_{Z\setminus D}\cong {\rm\Omega}_{Z\setminus D}^{r}$ by the projection formula. Let ![]() $U$ be any open set in
$U$ be any open set in ![]() $Z$, and let
$Z$, and let ![]() ${\it\beta}$ be any element of
${\it\beta}$ be any element of ![]() $\mathscr{M}(U)$, that is, a section of
$\mathscr{M}(U)$, that is, a section of ![]() $\mathscr{M}|_{U}$. Then
$\mathscr{M}|_{U}$. Then ![]() ${\it\beta}$ is a rational section of
${\it\beta}$ is a rational section of ![]() ${\rm\Omega}_{Z}^{r}|_{U}$ which can only have a pole along
${\rm\Omega}_{Z}^{r}|_{U}$ which can only have a pole along ![]() $D$ since
$D$ since 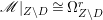 $\mathscr{M}|_{Z\setminus D}\cong {\rm\Omega}_{Z\setminus D}^{r}$. However, by the definition of
$\mathscr{M}|_{Z\setminus D}\cong {\rm\Omega}_{Z\setminus D}^{r}$. However, by the definition of ![]() $\mathscr{M}$,
$\mathscr{M}$, ![]() ${\it\beta}$ induces a regular section of
${\it\beta}$ induces a regular section of ![]() ${\rm\Omega}_{X}^{r}$ on the smooth locus of
${\rm\Omega}_{X}^{r}$ on the smooth locus of ![]() $p^{-1}(U)$. This implies that
$p^{-1}(U)$. This implies that ![]() ${\it\beta}$ does not have pole along
${\it\beta}$ does not have pole along ![]() $D$. Thus,
$D$. Thus, 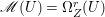 $\mathscr{M}(U)={\rm\Omega}_{Z}^{r}(U)$. Hence,
$\mathscr{M}(U)={\rm\Omega}_{Z}^{r}(U)$. Hence, 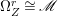 ${\rm\Omega}_{Z}^{r}\cong \mathscr{M}$.◻
${\rm\Omega}_{Z}^{r}\cong \mathscr{M}$.◻
Lemma 4.7. Let 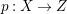 $p:X\rightarrow Z$ be an equidimensional fibration from a normal variety
$p:X\rightarrow Z$ be an equidimensional fibration from a normal variety ![]() $X$ to a smooth variety
$X$ to a smooth variety ![]() $Z$. Let
$Z$. Let 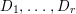 $D_{1},\ldots ,D_{r}$ be all the prime divisors in
$D_{1},\ldots ,D_{r}$ be all the prime divisors in ![]() $Z$ such that the multiplicity
$Z$ such that the multiplicity 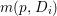 $m(p,D_{i})$ is larger than
$m(p,D_{i})$ is larger than ![]() $1$. If
$1$. If 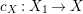 $c_{X}:X_{1}\rightarrow X$ is a finite morphism which is étale in codimension
$c_{X}:X_{1}\rightarrow X$ is a finite morphism which is étale in codimension ![]() $1$ and
$1$ and 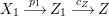 $X_{1}\overset{p_{1}}{\longrightarrow }Z_{1}\overset{c_{Z}}{\longrightarrow }Z$ is the Stein factorization, then
$X_{1}\overset{p_{1}}{\longrightarrow }Z_{1}\overset{c_{Z}}{\longrightarrow }Z$ is the Stein factorization, then 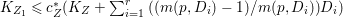 $K_{Z_{1}}\leqslant c_{Z}^{\ast }(K_{Z}+\sum _{i=1}^{r}((m(p,D_{i})-1)/m(p,D_{i}))D_{i})$. That is, there is an effective
$K_{Z_{1}}\leqslant c_{Z}^{\ast }(K_{Z}+\sum _{i=1}^{r}((m(p,D_{i})-1)/m(p,D_{i}))D_{i})$. That is, there is an effective ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() ${\rm\Delta}_{1}$ on
${\rm\Delta}_{1}$ on ![]() $Z_{1}$ such that
$Z_{1}$ such that
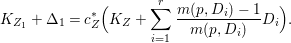 $$\begin{eqnarray}K_{Z_{1}}+{\rm\Delta}_{1}=c_{Z}^{\ast }(K_{Z}+\mathop{\sum }_{i=1}^{r}\frac{m(p,D_{i})-1}{m(p,D_{i})}D_{i}).\end{eqnarray}$$
$$\begin{eqnarray}K_{Z_{1}}+{\rm\Delta}_{1}=c_{Z}^{\ast }(K_{Z}+\mathop{\sum }_{i=1}^{r}\frac{m(p,D_{i})-1}{m(p,D_{i})}D_{i}).\end{eqnarray}$$Proof. If ![]() $D$ is a prime divisor in
$D$ is a prime divisor in ![]() $Z$, then
$Z$, then 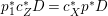 $p_{1}^{\ast }c_{Z}^{\ast }D=c_{X}^{\ast }p^{\ast }D$. Let
$p_{1}^{\ast }c_{Z}^{\ast }D=c_{X}^{\ast }p^{\ast }D$. Let ![]() $E$ be any irreducible component of
$E$ be any irreducible component of ![]() $c_{Z}^{\ast }D$. Since
$c_{Z}^{\ast }D$. Since ![]() $c_{X}$ is étale in codimension
$c_{X}$ is étale in codimension ![]() $1$, by comparing the coefficients of
$1$, by comparing the coefficients of ![]() $E$ in
$E$ in 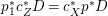 $p_{1}^{\ast }c_{Z}^{\ast }D=c_{X}^{\ast }p^{\ast }D$, the coefficient
$p_{1}^{\ast }c_{Z}^{\ast }D=c_{X}^{\ast }p^{\ast }D$, the coefficient ![]() $m_{E}$ of
$m_{E}$ of ![]() $E$ in
$E$ in ![]() $c_{Z}^{\ast }D$ is not larger than
$c_{Z}^{\ast }D$ is not larger than 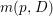 $m(p,D)$. This implies that
$m(p,D)$. This implies that 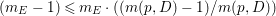 $(m_{E}-1)\leqslant m_{E}\cdot ((m(p,D)-1)/m(p,D))$. Now, from Lemma 4.3, we obtain
$(m_{E}-1)\leqslant m_{E}\cdot ((m(p,D)-1)/m(p,D))$. Now, from Lemma 4.3, we obtain 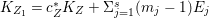 $K_{Z_{1}}=c_{Z}^{\ast }K_{Z}+{\rm\Sigma}_{j=1}^{s}(m_{j}-1)E_{j}$, where the
$K_{Z_{1}}=c_{Z}^{\ast }K_{Z}+{\rm\Sigma}_{j=1}^{s}(m_{j}-1)E_{j}$, where the ![]() $E_{j}$ are all prime divisors along which
$E_{j}$ are all prime divisors along which ![]() $c_{Z}^{\ast }$ is ramified, and
$c_{Z}^{\ast }$ is ramified, and ![]() $m_{j}$ is the degree of ramification of
$m_{j}$ is the degree of ramification of ![]() $c_{Z}$ along
$c_{Z}$ along ![]() $E_{j}$. By the discussion above, we have
$E_{j}$. By the discussion above, we have 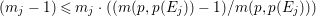 $(m_{j}-1)\leqslant m_{j}\cdot ((m(p,p(E_{j}))-1)/m(p,p(E_{j})))$. Hence,
$(m_{j}-1)\leqslant m_{j}\cdot ((m(p,p(E_{j}))-1)/m(p,p(E_{j})))$. Hence, 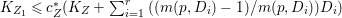 $K_{Z_{1}}\leqslant c_{Z}^{\ast }(K_{Z}+\sum _{i=1}^{r}((m(p,D_{i})-1)/m(p,D_{i}))D_{i})$.◻
$K_{Z_{1}}\leqslant c_{Z}^{\ast }(K_{Z}+\sum _{i=1}^{r}((m(p,D_{i})-1)/m(p,D_{i}))D_{i})$.◻
Lemma 4.8. Let 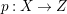 $p:X\rightarrow Z$ be a Mori fibration from a normal threefold
$p:X\rightarrow Z$ be a Mori fibration from a normal threefold ![]() $X$ to a smooth surface
$X$ to a smooth surface ![]() $Z$. Let
$Z$. Let 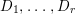 $D_{1},\ldots ,D_{r}$ be all the prime divisors in
$D_{1},\ldots ,D_{r}$ be all the prime divisors in ![]() $Z$ such that the multiplicity
$Z$ such that the multiplicity 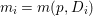 $m_{i}=m(p,D_{i})$ is larger than
$m_{i}=m(p,D_{i})$ is larger than ![]() $1$. Assume that there is a projective
$1$. Assume that there is a projective ![]() $\mathbb{Q}$-factorial variety
$\mathbb{Q}$-factorial variety ![]() $V$ such that we have an open embedding
$V$ such that we have an open embedding 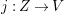 $j:Z\rightarrow V$ with
$j:Z\rightarrow V$ with 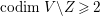 $\text{codim}\,V\setminus Z\geqslant 2$. Assume further that the pair
$\text{codim}\,V\setminus Z\geqslant 2$. Assume further that the pair 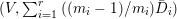 $(V,\sum _{i=1}^{r}((m_{i}-1)/m_{i})\bar{D}_{i})$ is klt, where
$(V,\sum _{i=1}^{r}((m_{i}-1)/m_{i})\bar{D}_{i})$ is klt, where ![]() $\bar{D}_{i}$ is the closure of
$\bar{D}_{i}$ is the closure of ![]() $\bar{D}_{i}$ in
$\bar{D}_{i}$ in ![]() $V$. If
$V$. If ![]() $\mathscr{F}$ is a rank-
$\mathscr{F}$ is a rank-![]() $1$ reflexive subsheaf of
$1$ reflexive subsheaf of ![]() ${\rm\Omega}_{X}^{[1]}$ such that
${\rm\Omega}_{X}^{[1]}$ such that 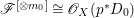 $\mathscr{F}^{[\otimes m_{0}]}\cong \mathscr{O}_{X}(p^{\ast }D_{0})$ for some positive integer
$\mathscr{F}^{[\otimes m_{0}]}\cong \mathscr{O}_{X}(p^{\ast }D_{0})$ for some positive integer ![]() $m_{0}$ and some divisor
$m_{0}$ and some divisor ![]() $D_{0}$ on
$D_{0}$ on ![]() $Z$, then
$Z$, then ![]() $\bar{D}_{0}$, the closure of
$\bar{D}_{0}$, the closure of ![]() $D_{0}$ in
$D_{0}$ in ![]() $V$, is not ample.
$V$, is not ample.
Proof. Assume the opposite. First, we assume further that ![]() $m_{0}=1$ and
$m_{0}=1$ and 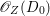 $\mathscr{O}_{Z}(D_{0})$ has non-zero global sections. Let
$\mathscr{O}_{Z}(D_{0})$ has non-zero global sections. Let 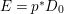 $E=p^{\ast }D_{0}$, which is effective. Then
$E=p^{\ast }D_{0}$, which is effective. Then 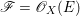 $\mathscr{F}=\mathscr{O}_{X}(E)$. Since general fibers of
$\mathscr{F}=\mathscr{O}_{X}(E)$. Since general fibers of ![]() $p$ are isomorphic to
$p$ are isomorphic to ![]() $\mathbb{P}^{1}$, which does not carry any non-zero pluri-forms, by Lemma 2.5, the injection
$\mathbb{P}^{1}$, which does not carry any non-zero pluri-forms, by Lemma 2.5, the injection 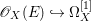 $\mathscr{O}_{X}(E){\hookrightarrow}{\rm\Omega}_{X}^{[1]}$ factorizes through
$\mathscr{O}_{X}(E){\hookrightarrow}{\rm\Omega}_{X}^{[1]}$ factorizes through 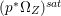 $(p^{\ast }{\rm\Omega}_{Z})^{sat}$. Hence, by the projection formula, we have an injection from
$(p^{\ast }{\rm\Omega}_{Z})^{sat}$. Hence, by the projection formula, we have an injection from 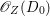 $\mathscr{O}_{Z}(D_{0})$ to
$\mathscr{O}_{Z}(D_{0})$ to 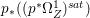 $p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})$. However, by Lemma 4.6, we have
$p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})$. However, by Lemma 4.6, we have 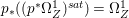 $p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})={\rm\Omega}_{Z}^{1}$. By Proposition 2.1, we get an injection from
$p_{\ast }((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})={\rm\Omega}_{Z}^{1}$. By Proposition 2.1, we get an injection from 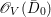 $\mathscr{O}_{V}(\bar{D}_{0})$ to
$\mathscr{O}_{V}(\bar{D}_{0})$ to ![]() ${\rm\Omega}_{V}^{[1]}$. Hence, by the Bogomolov–Sommese theorem (see [Reference GrafGra15, Corollary 1.3]), the Kodaira dimension of
${\rm\Omega}_{V}^{[1]}$. Hence, by the Bogomolov–Sommese theorem (see [Reference GrafGra15, Corollary 1.3]), the Kodaira dimension of 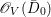 $\mathscr{O}_{V}(\bar{D}_{0})$ is not larger than
$\mathscr{O}_{V}(\bar{D}_{0})$ is not larger than ![]() $1$. Hence,
$1$. Hence, ![]() $\bar{D}_{0}$ is not ample. We obtain a contradiction.
$\bar{D}_{0}$ is not ample. We obtain a contradiction.
Now we treat the general case. We show that we can reduce to the previous case. By replacing ![]() $m_{0}$ with a large multiple, we may assume that
$m_{0}$ with a large multiple, we may assume that ![]() $\bar{D}_{0}$ is very ample. We may also assume that both
$\bar{D}_{0}$ is very ample. We may also assume that both ![]() $\bar{D}_{0}$ and
$\bar{D}_{0}$ and ![]() $p^{\ast }D_{0}$ are prime and that the pair
$p^{\ast }D_{0}$ are prime and that the pair 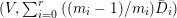 $(V,\sum _{i=0}^{r}((m_{i}-1)/m_{i})\bar{D}_{i})$ is klt. Let
$(V,\sum _{i=0}^{r}((m_{i}-1)/m_{i})\bar{D}_{i})$ is klt. Let 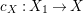 $c_{X}:X_{1}\rightarrow X$ be the normalization of the ramified cyclic cover with respect to
$c_{X}:X_{1}\rightarrow X$ be the normalization of the ramified cyclic cover with respect to ![]() $\mathscr{F}$,
$\mathscr{F}$, ![]() $m_{0}$ and
$m_{0}$ and ![]() $p^{\ast }D_{0}$ (see [Reference Kollár and MoriKM98, Definition 2.52]). Then
$p^{\ast }D_{0}$ (see [Reference Kollár and MoriKM98, Definition 2.52]). Then ![]() $c_{X}$ is ramified over
$c_{X}$ is ramified over ![]() $p^{\ast }D_{0}$ with degree
$p^{\ast }D_{0}$ with degree ![]() $m$ and
$m$ and 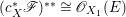 $(c_{X}^{\ast }\mathscr{F})^{\ast \ast }\cong \mathscr{O}_{X_{1}}(E)$, where
$(c_{X}^{\ast }\mathscr{F})^{\ast \ast }\cong \mathscr{O}_{X_{1}}(E)$, where 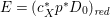 $E=(c_{X}^{\ast }p^{\ast }D_{0})_{\mathit{red}}$. Moreover, over the smooth locus of
$E=(c_{X}^{\ast }p^{\ast }D_{0})_{\mathit{red}}$. Moreover, over the smooth locus of ![]() $X$, there is an injection of sheaves from
$X$, there is an injection of sheaves from ![]() $c_{X}^{\ast }{\rm\Omega}_{X}^{1}$ to
$c_{X}^{\ast }{\rm\Omega}_{X}^{1}$ to ![]() ${\rm\Omega}_{X_{1}}^{1}$. Hence, by Proposition 2.1, we have an injection
${\rm\Omega}_{X_{1}}^{1}$. Hence, by Proposition 2.1, we have an injection 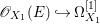 $\mathscr{O}_{X_{1}}(E){\hookrightarrow}{\rm\Omega}_{X_{1}}^{[1]}$.
$\mathscr{O}_{X_{1}}(E){\hookrightarrow}{\rm\Omega}_{X_{1}}^{[1]}$.
Let 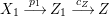 $X_{1}\overset{p_{1}}{\longrightarrow }Z_{1}\overset{c_{Z}}{\longrightarrow }Z$ be the Stein factorization. Let
$X_{1}\overset{p_{1}}{\longrightarrow }Z_{1}\overset{c_{Z}}{\longrightarrow }Z$ be the Stein factorization. Let 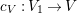 $c_{V}:V_{1}\rightarrow V$ be the normalization of
$c_{V}:V_{1}\rightarrow V$ be the normalization of ![]() $V$ in the function field of
$V$ in the function field of ![]() $X_{1}$. Then we obtain an open embedding
$X_{1}$. Then we obtain an open embedding 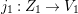 $j_{1}:Z_{1}\rightarrow V_{1}$ such that
$j_{1}:Z_{1}\rightarrow V_{1}$ such that 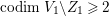 $\text{codim}\,V_{1}\setminus Z_{1}\geqslant 2$. If
$\text{codim}\,V_{1}\setminus Z_{1}\geqslant 2$. If ![]() $F_{p}$ is a general fiber of
$F_{p}$ is a general fiber of ![]() $p$ and if
$p$ and if ![]() $F_{p_{1}}$ is a general fiber of
$F_{p_{1}}$ is a general fiber of ![]() $p_{1}$ which is mapped to
$p_{1}$ which is mapped to ![]() $F_{p}$, then
$F_{p}$, then 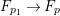 $F_{p_{1}}\rightarrow F_{p}$ is étale. Since
$F_{p_{1}}\rightarrow F_{p}$ is étale. Since ![]() $p$ is a Mori fibration,
$p$ is a Mori fibration, ![]() $F_{p}$ is a smooth rational curve which is simply connected. Hence,
$F_{p}$ is a smooth rational curve which is simply connected. Hence, 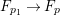 $F_{p_{1}}\rightarrow F_{p}$ is an isomorphism and
$F_{p_{1}}\rightarrow F_{p}$ is an isomorphism and 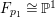 $F_{p_{1}}\cong \mathbb{P}^{1}$. Hence,
$F_{p_{1}}\cong \mathbb{P}^{1}$. Hence, ![]() $c_{Z}$ is of degree
$c_{Z}$ is of degree ![]() $m_{0}$. Let
$m_{0}$. Let 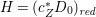 $H=(c_{Z}^{\ast }D_{0})_{\mathit{red}}$. Since
$H=(c_{Z}^{\ast }D_{0})_{\mathit{red}}$. Since 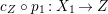 $c_{Z}\circ p_{1}:X_{1}\rightarrow Z$ has connected fibers over
$c_{Z}\circ p_{1}:X_{1}\rightarrow Z$ has connected fibers over ![]() $D_{0}$, we have
$D_{0}$, we have 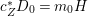 $c_{Z}^{\ast }D_{0}=m_{0}H$. Hence,
$c_{Z}^{\ast }D_{0}=m_{0}H$. Hence, 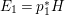 $E_{1}=p_{1}^{\ast }H$. Let
$E_{1}=p_{1}^{\ast }H$. Let ![]() $\bar{H}$ be the closure of
$\bar{H}$ be the closure of ![]() $H$ in
$H$ in ![]() $V_{1}$. Then it is ample since
$V_{1}$. Then it is ample since ![]() $c_{V}$ is finite.
$c_{V}$ is finite.
Note that 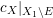 $c_{X}|_{X_{1}\setminus E}$ is étale in codimension
$c_{X}|_{X_{1}\setminus E}$ is étale in codimension ![]() $1$ and
$1$ and 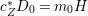 $c_{Z}^{\ast }D_{0}=m_{0}H$. By Lemma 4.7, we conclude that there is an effective
$c_{Z}^{\ast }D_{0}=m_{0}H$. By Lemma 4.7, we conclude that there is an effective ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() ${\rm\Delta}_{1}^{\prime }$ in
${\rm\Delta}_{1}^{\prime }$ in ![]() $Z_{1}$ such that
$Z_{1}$ such that 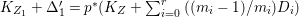 $K_{Z_{1}}+{\rm\Delta}_{1}^{\prime }=p^{\ast }(K_{Z}+\sum _{i=0}^{r}((m_{i}-1)/m_{i})D_{i})$. Hence, if
$K_{Z_{1}}+{\rm\Delta}_{1}^{\prime }=p^{\ast }(K_{Z}+\sum _{i=0}^{r}((m_{i}-1)/m_{i})D_{i})$. Hence, if ![]() ${\rm\Delta}_{1}$ is the closure of
${\rm\Delta}_{1}$ is the closure of ![]() ${\rm\Delta}_{1}^{\prime }$ in
${\rm\Delta}_{1}^{\prime }$ in ![]() $V_{1}$, then
$V_{1}$, then 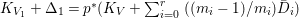 $K_{V_{1}}+{\rm\Delta}_{1}=p^{\ast }(K_{V}+\sum _{i=0}^{r}((m_{i}-1)/m_{i})\bar{D}_{i})$. This implies that
$K_{V_{1}}+{\rm\Delta}_{1}=p^{\ast }(K_{V}+\sum _{i=0}^{r}((m_{i}-1)/m_{i})\bar{D}_{i})$. This implies that  $(V_{1},{\rm\Delta}_{1})$ is klt by [Reference Kollár and MoriKM98, Proposition 5.20 and Corollary 2.35].
$(V_{1},{\rm\Delta}_{1})$ is klt by [Reference Kollár and MoriKM98, Proposition 5.20 and Corollary 2.35].
Hence, 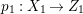 $p_{1}:X_{1}\rightarrow Z_{1}$ satisfies the conditions in the lemma. There is an injection from
$p_{1}:X_{1}\rightarrow Z_{1}$ satisfies the conditions in the lemma. There is an injection from ![]() $\mathscr{O}_{X_{1}}(E)$ to
$\mathscr{O}_{X_{1}}(E)$ to ![]() ${\rm\Omega}_{X_{1}}^{[1]}$, and
${\rm\Omega}_{X_{1}}^{[1]}$, and 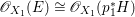 $\mathscr{O}_{X_{1}}(E)\cong \mathscr{O}_{X_{1}}(p_{1}^{\ast }H)$, such that
$\mathscr{O}_{X_{1}}(E)\cong \mathscr{O}_{X_{1}}(p_{1}^{\ast }H)$, such that ![]() $\bar{H}$ is ample in
$\bar{H}$ is ample in ![]() $V_{1}$. We are in the same situation as in the first case. This leads to a contradiction.◻
$V_{1}$. We are in the same situation as in the first case. This leads to a contradiction.◻
Lemma 4.9. Let 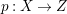 $p:X\rightarrow Z$ be an equidimensional fibration such that general fibers of
$p:X\rightarrow Z$ be an equidimensional fibration such that general fibers of ![]() $p$ do not carry any non-zero pluri-forms. Assume that
$p$ do not carry any non-zero pluri-forms. Assume that ![]() $Z$ is smooth and that there is an open embedding
$Z$ is smooth and that there is an open embedding 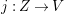 $j:Z\rightarrow V$ such that
$j:Z\rightarrow V$ such that 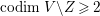 $\text{codim}\,V\setminus Z\geqslant 2$. Assume that
$\text{codim}\,V\setminus Z\geqslant 2$. Assume that 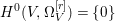 $H^{0}(V,{\rm\Omega}_{V}^{[r]})=\{0\}$ for all
$H^{0}(V,{\rm\Omega}_{V}^{[r]})=\{0\}$ for all ![]() $r>0$. Then
$r>0$. Then 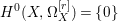 $H^{0}(X,{\rm\Omega}_{X}^{[r]})=\{0\}$ for all
$H^{0}(X,{\rm\Omega}_{X}^{[r]})=\{0\}$ for all ![]() $r>0$.
$r>0$.
Proof. Assume the opposite. Let 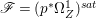 $\mathscr{F}=(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ be the saturation of the image of
$\mathscr{F}=(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ be the saturation of the image of ![]() $p^{\ast }{\rm\Omega}_{Z}^{1}$ in
$p^{\ast }{\rm\Omega}_{Z}^{1}$ in ![]() ${\rm\Omega}_{X}^{[1]}$. Since general fibers of
${\rm\Omega}_{X}^{[1]}$. Since general fibers of ![]() $p$ do not carry any non-zero pluri-forms, we have
$p$ do not carry any non-zero pluri-forms, we have 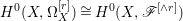 $H^{0}(X,{\rm\Omega}_{X}^{[r]})\cong H^{0}(X,\mathscr{F}^{[\wedge r]})$ by Lemma 2.5. Hence, there is an injection from
$H^{0}(X,{\rm\Omega}_{X}^{[r]})\cong H^{0}(X,\mathscr{F}^{[\wedge r]})$ by Lemma 2.5. Hence, there is an injection from ![]() $\mathscr{O}_{X}$ to
$\mathscr{O}_{X}$ to ![]() $\mathscr{F}^{[\wedge r]}$. By taking the direct image, we have an injection from
$\mathscr{F}^{[\wedge r]}$. By taking the direct image, we have an injection from ![]() $\mathscr{O}_{Z}$ to
$\mathscr{O}_{Z}$ to 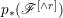 $p_{\ast }(\mathscr{F}^{[\wedge r]})$. By Lemma 4.6,
$p_{\ast }(\mathscr{F}^{[\wedge r]})$. By Lemma 4.6, 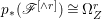 $p_{\ast }(\mathscr{F}^{[\wedge r]})\cong {\rm\Omega}_{Z}^{r}$. This implies that
$p_{\ast }(\mathscr{F}^{[\wedge r]})\cong {\rm\Omega}_{Z}^{r}$. This implies that 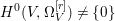 $H^{0}(V,{\rm\Omega}_{V}^{[r]})\neq \{0\}$ by Proposition 2.1, which is a contradiction.◻
$H^{0}(V,{\rm\Omega}_{V}^{[r]})\neq \{0\}$ by Proposition 2.1, which is a contradiction.◻
Now we are ready to prove Theorem 4.2.
Proof of Theorem 4.2.
We argue by contradiction. Let 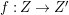 $f:Z\rightarrow Z^{\prime }$ be the result of a
$f:Z\rightarrow Z^{\prime }$ be the result of a 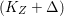 $(K_{Z}+{\rm\Delta})$-MMP. Assume that
$(K_{Z}+{\rm\Delta})$-MMP. Assume that ![]() $Z^{\prime }$ has Picard number
$Z^{\prime }$ has Picard number ![]() $1$. Set
$1$. Set 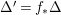 ${\rm\Delta}^{\prime }=f_{\ast }{\rm\Delta}$. Then
${\rm\Delta}^{\prime }=f_{\ast }{\rm\Delta}$. Then 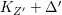 $K_{Z^{\prime }}+{\rm\Delta}^{\prime }$ is not pseudo-effective either. Thus,
$K_{Z^{\prime }}+{\rm\Delta}^{\prime }$ is not pseudo-effective either. Thus,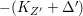 $-(K_{Z^{\prime }}+{\rm\Delta}^{\prime })$ is ample. We know that there is a smooth open subset
$-(K_{Z^{\prime }}+{\rm\Delta}^{\prime })$ is ample. We know that there is a smooth open subset 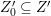 $Z_{0}^{\prime }\subseteq Z^{\prime }$ with
$Z_{0}^{\prime }\subseteq Z^{\prime }$ with 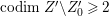 $\text{codim}\,Z^{\prime }\setminus Z_{0}^{\prime }\geqslant 2$ such that
$\text{codim}\,Z^{\prime }\setminus Z_{0}^{\prime }\geqslant 2$ such that ![]() $f^{-1}$ is an isomorphism from
$f^{-1}$ is an isomorphism from ![]() $Z_{0}^{\prime }$ onto its image. Let
$Z_{0}^{\prime }$ onto its image. Let ![]() $Z_{0}$ be
$Z_{0}$ be 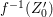 $f^{-1}(Z_{0}^{\prime })$, which is an open subset in
$f^{-1}(Z_{0}^{\prime })$, which is an open subset in ![]() $Z$. Let
$Z$. Let 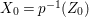 $X_{0}=p^{-1}(Z_{0})$.
$X_{0}=p^{-1}(Z_{0})$.
Since 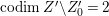 $\text{codim}\,Z^{\prime }\setminus Z_{0}^{\prime }=2$, there is a projective curve
$\text{codim}\,Z^{\prime }\setminus Z_{0}^{\prime }=2$, there is a projective curve ![]() $C_{0}^{\prime }$ in
$C_{0}^{\prime }$ in ![]() $Z_{0}^{\prime }$ such that it is an ample divisor in
$Z_{0}^{\prime }$ such that it is an ample divisor in ![]() $Z^{\prime }$. Let
$Z^{\prime }$. Let ![]() $C_{0}$ be the strict transform of
$C_{0}$ be the strict transform of ![]() $C_{0}^{\prime }$ in
$C_{0}^{\prime }$ in ![]() $Z_{0}$. Let
$Z_{0}$. Let ![]() ${\it\alpha}$ be the class of the curve
${\it\alpha}$ be the class of the curve 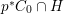 $p^{\ast }C_{0}\cap H$, where
$p^{\ast }C_{0}\cap H$, where ![]() $H$ is a very ample divisor in
$H$ is a very ample divisor in ![]() $X$. Then the class
$X$. Then the class ![]() ${\it\alpha}$ is movable and
${\it\alpha}$ is movable and ![]() $p_{\ast }{\it\alpha}$ is proportional to the class of
$p_{\ast }{\it\alpha}$ is proportional to the class of ![]() $C_{0}$.
$C_{0}$.
Since general fibers of ![]() $p$ do not carry any non-zero pluri-forms, by Lemma 2.5, we obtain that
$p$ do not carry any non-zero pluri-forms, by Lemma 2.5, we obtain that
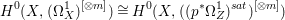 $$\begin{eqnarray}H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]})\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]})\end{eqnarray}$$ for any ![]() $m>0$, where
$m>0$, where 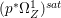 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ is the saturation of the image of
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ is the saturation of the image of ![]() $(p^{\ast }{\rm\Omega}_{Z}^{1})$ in
$(p^{\ast }{\rm\Omega}_{Z}^{1})$ in ![]() ${\rm\Omega}_{X}^{[1]}$. Hence,
${\rm\Omega}_{X}^{[1]}$. Hence, 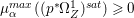 ${\it\mu}_{{\it\alpha}}^{max}((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})\geqslant 0$ and there is a coherent sheaf
${\it\mu}_{{\it\alpha}}^{max}((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})\geqslant 0$ and there is a coherent sheaf ![]() $\mathscr{H}$ saturated in
$\mathscr{H}$ saturated in 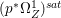 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ such that
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ such that 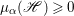 ${\it\mu}_{{\it\alpha}}(\mathscr{H})\geqslant 0$.
${\it\mu}_{{\it\alpha}}(\mathscr{H})\geqslant 0$.
However, since ![]() $p|_{X_{0}}$ is a Mori fibration and
$p|_{X_{0}}$ is a Mori fibration and ![]() $Z_{0}$ is smooth, the
$Z_{0}$ is smooth, the ![]() $\mathbb{Q}$-Cartier divisor which associates to the determinant of
$\mathbb{Q}$-Cartier divisor which associates to the determinant of 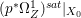 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}|_{X_{0}}$ is equal to
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}|_{X_{0}}$ is equal to 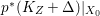 $p^{\ast }(K_{Z}+{\rm\Delta})|_{X_{0}}$ by Remark 4.5. Hence,
$p^{\ast }(K_{Z}+{\rm\Delta})|_{X_{0}}$ by Remark 4.5. Hence,
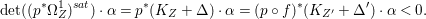 $$\begin{eqnarray}\text{det}((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})\cdot {\it\alpha}=p^{\ast }(K_{Z}+{\rm\Delta})\cdot {\it\alpha}=(p\circ f)^{\ast }(K_{Z^{\prime }}+{\rm\Delta}^{\prime })\cdot {\it\alpha}<0.\end{eqnarray}$$
$$\begin{eqnarray}\text{det}((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})\cdot {\it\alpha}=p^{\ast }(K_{Z}+{\rm\Delta})\cdot {\it\alpha}=(p\circ f)^{\ast }(K_{Z^{\prime }}+{\rm\Delta}^{\prime })\cdot {\it\alpha}<0.\end{eqnarray}$$ This implies that 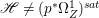 $\mathscr{H}\neq (p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$. If
$\mathscr{H}\neq (p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$. If ![]() $\mathscr{J}$ is the quotient
$\mathscr{J}$ is the quotient 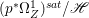 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}/\mathscr{H}$, then
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}/\mathscr{H}$, then 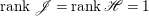 $\text{rank}\,\mathscr{J}=\text{rank}\,\mathscr{H}=1$ and
$\text{rank}\,\mathscr{J}=\text{rank}\,\mathscr{H}=1$ and 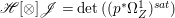 $\mathscr{H}[\otimes ]\mathscr{J}=\text{det}\,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})$. Thus,
$\mathscr{H}[\otimes ]\mathscr{J}=\text{det}\,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})$. Thus, 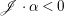 $\mathscr{J}\cdot {\it\alpha}<0$.
$\mathscr{J}\cdot {\it\alpha}<0$.
Since 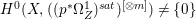 $H^{0}(X,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]})\neq \{0\}$ for some
$H^{0}(X,((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})^{[\otimes m]})\neq \{0\}$ for some ![]() $m>0$, we have
$m>0$, we have
 $$\begin{eqnarray}H^{0}(X,\mathscr{H}^{\otimes s}[\otimes ]\mathscr{J}^{\otimes t})\neq \{0\}\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(X,\mathscr{H}^{\otimes s}[\otimes ]\mathscr{J}^{\otimes t})\neq \{0\}\end{eqnarray}$$ for some ![]() $s,t\geqslant 0$ by Proposition 2.1 and Lemma 2.3. In this case, we have
$s,t\geqslant 0$ by Proposition 2.1 and Lemma 2.3. In this case, we have ![]() $s>t$ for
$s>t$ for 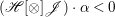 $(\mathscr{H}[\otimes ]\mathscr{J})\cdot {\it\alpha}<0$ and
$(\mathscr{H}[\otimes ]\mathscr{J})\cdot {\it\alpha}<0$ and 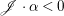 $\mathscr{J}\cdot {\it\alpha}<0$.
$\mathscr{J}\cdot {\it\alpha}<0$.
Let ![]() $F_{p}$ be a general fiber of
$F_{p}$ be a general fiber of ![]() $p$. Then the class of
$p$. Then the class of ![]() $F_{p}$ is movable. Hence,
$F_{p}$ is movable. Hence, 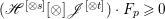 $(\mathscr{H}^{[\otimes s]}[\otimes ]\mathscr{J}^{[\otimes t]})\cdot F_{p}\geqslant 0$. Moreover, we have
$(\mathscr{H}^{[\otimes s]}[\otimes ]\mathscr{J}^{[\otimes t]})\cdot F_{p}\geqslant 0$. Moreover, we have
 $$\begin{eqnarray}(\mathscr{H}[\otimes ]\mathscr{J})\cdot F_{p}=\text{det}((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})\cdot F_{p}=0.\end{eqnarray}$$
$$\begin{eqnarray}(\mathscr{H}[\otimes ]\mathscr{J})\cdot F_{p}=\text{det}((p^{\ast }{\rm\Omega}_{Z}^{1})^{sat})\cdot F_{p}=0.\end{eqnarray}$$ This implies that 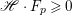 $\mathscr{H}\cdot F_{p}\geqslant 0$ since
$\mathscr{H}\cdot F_{p}\geqslant 0$ since ![]() $s>t$. However, since the restriction of
$s>t$. However, since the restriction of 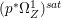 $(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ on
$(p^{\ast }{\rm\Omega}_{Z}^{1})^{sat}$ on ![]() $F_{p}$ is isomorphic to
$F_{p}$ is isomorphic to 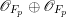 $\mathscr{O}_{F_{p}}\oplus \mathscr{O}_{F_{p}}$, we have
$\mathscr{O}_{F_{p}}\oplus \mathscr{O}_{F_{p}}$, we have 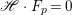 $\mathscr{H}\cdot F_{p}=0$.
$\mathscr{H}\cdot F_{p}=0$.
Let ![]() $k$ be the smallest positive integer such that
$k$ be the smallest positive integer such that ![]() $\mathscr{H}^{[\otimes k]}$ is invertible. Then there is a Cartier divisor
$\mathscr{H}^{[\otimes k]}$ is invertible. Then there is a Cartier divisor ![]() $L$ in
$L$ in ![]() $Z$ such that
$Z$ such that 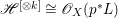 $\mathscr{H}^{[\otimes k]}\cong \mathscr{O}_{X}(p^{\ast }L)$. Let
$\mathscr{H}^{[\otimes k]}\cong \mathscr{O}_{X}(p^{\ast }L)$. Let 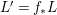 $L^{\prime }=f_{\ast }L$. Then
$L^{\prime }=f_{\ast }L$. Then 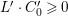 $L^{\prime }\cdot C_{0}^{\prime }\geqslant 0$ since
$L^{\prime }\cdot C_{0}^{\prime }\geqslant 0$ since 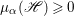 ${\it\mu}_{{\it\alpha}}(\mathscr{H})\geqslant 0$. Note that if
${\it\mu}_{{\it\alpha}}(\mathscr{H})\geqslant 0$. Note that if 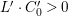 $L^{\prime }\cdot C_{0}^{\prime }>0$, then
$L^{\prime }\cdot C_{0}^{\prime }>0$, then ![]() $L^{\prime }$ is ample on
$L^{\prime }$ is ample on ![]() $Z^{\prime }$ since
$Z^{\prime }$ since ![]() $Z^{\prime }$ has Picard number
$Z^{\prime }$ has Picard number ![]() $1$. Hence, by Lemma 4.8, we can only have
$1$. Hence, by Lemma 4.8, we can only have 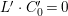 $L^{\prime }\cdot C_{0}^{\prime }=0$, and
$L^{\prime }\cdot C_{0}^{\prime }=0$, and ![]() $L^{\prime }$ is numerically equal to the zero divisor since
$L^{\prime }$ is numerically equal to the zero divisor since ![]() $Z^{\prime }$ has Picard number
$Z^{\prime }$ has Picard number ![]() $1$. By [Reference Araujo and DruelAD14, Lemma 2.6], there is a positive integer
$1$. By [Reference Araujo and DruelAD14, Lemma 2.6], there is a positive integer ![]() $k^{\prime }$ such that
$k^{\prime }$ such that ![]() $k^{\prime }L^{\prime }$ is linearly equivalent to the zero divisor. Hence,
$k^{\prime }L^{\prime }$ is linearly equivalent to the zero divisor. Hence, 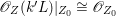 $\mathscr{O}_{Z}(k^{\prime }L)|_{Z_{0}}\cong \mathscr{O}_{Z_{0}}$ and
$\mathscr{O}_{Z}(k^{\prime }L)|_{Z_{0}}\cong \mathscr{O}_{Z_{0}}$ and 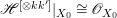 $\mathscr{H}^{[\otimes kk^{\prime }]}|_{X_{0}}\cong \mathscr{O}_{X_{0}}$. Let
$\mathscr{H}^{[\otimes kk^{\prime }]}|_{X_{0}}\cong \mathscr{O}_{X_{0}}$. Let ![]() $l$ be the smallest positive integer such that
$l$ be the smallest positive integer such that 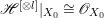 $\mathscr{H}^{[\otimes l]}|_{X_{0}}\cong \mathscr{O}_{X_{0}}$. Let
$\mathscr{H}^{[\otimes l]}|_{X_{0}}\cong \mathscr{O}_{X_{0}}$. Let 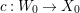 $c:W_{0}\rightarrow X_{0}$ be the normalization of the cyclic cover with respect to the isomorphism
$c:W_{0}\rightarrow X_{0}$ be the normalization of the cyclic cover with respect to the isomorphism 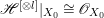 $\mathscr{H}^{[\otimes l]}|_{X_{0}}\cong \mathscr{O}_{X_{0}}$ (see [Reference Kollár and MoriKM98, Definition 2.52]). Then
$\mathscr{H}^{[\otimes l]}|_{X_{0}}\cong \mathscr{O}_{X_{0}}$ (see [Reference Kollár and MoriKM98, Definition 2.52]). Then ![]() $c$ is étale in codimension
$c$ is étale in codimension ![]() $1$. We have
$1$. We have 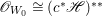 $\mathscr{O}_{W_{0}}\cong (c^{\ast }\mathscr{H})^{\ast \ast }$ and there is an injection
$\mathscr{O}_{W_{0}}\cong (c^{\ast }\mathscr{H})^{\ast \ast }$ and there is an injection 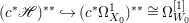 $(c^{\ast }\mathscr{H})^{\ast \ast }{\hookrightarrow}(c^{\ast }{\rm\Omega}_{X_{0}}^{1})^{\ast \ast }\cong {\rm\Omega}_{W_{0}}^{[1]}$. Hence,
$(c^{\ast }\mathscr{H})^{\ast \ast }{\hookrightarrow}(c^{\ast }{\rm\Omega}_{X_{0}}^{1})^{\ast \ast }\cong {\rm\Omega}_{W_{0}}^{[1]}$. Hence, 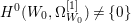 $H^{0}(W_{0},{\rm\Omega}_{W_{0}}^{[1]})\neq \{0\}$.
$H^{0}(W_{0},{\rm\Omega}_{W_{0}}^{[1]})\neq \{0\}$.
Let 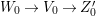 $W_{0}\rightarrow V_{0}\rightarrow Z_{0}^{\prime }$ be the Stein factorization. Let
$W_{0}\rightarrow V_{0}\rightarrow Z_{0}^{\prime }$ be the Stein factorization. Let 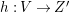 $h:V\rightarrow Z^{\prime }$ be the normalization of
$h:V\rightarrow Z^{\prime }$ be the normalization of ![]() $Z^{\prime }$ in the function field of
$Z^{\prime }$ in the function field of ![]() $W_{0}$. Then there is an open embedding from
$W_{0}$. Then there is an open embedding from ![]() $V_{0}$ to
$V_{0}$ to ![]() $V$ such that
$V$ such that 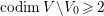 $\text{codim}\,V\setminus V_{0}\geqslant 2$. By Lemma 4.7, we have
$\text{codim}\,V\setminus V_{0}\geqslant 2$. By Lemma 4.7, we have 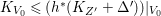 $K_{V_{0}}\leqslant (h^{\ast }(K_{Z^{\prime }}+{\rm\Delta}^{\prime }))|_{V_{0}}$. Since
$K_{V_{0}}\leqslant (h^{\ast }(K_{Z^{\prime }}+{\rm\Delta}^{\prime }))|_{V_{0}}$. Since 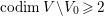 $\text{codim}\,V\setminus V_{0}\geqslant 2$, there is an effective
$\text{codim}\,V\setminus V_{0}\geqslant 2$, there is an effective ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() ${\rm\Delta}_{V}$ in
${\rm\Delta}_{V}$ in ![]() $V$ such that
$V$ such that 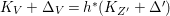 $K_{V}+{\rm\Delta}_{V}=h^{\ast }(K_{Z^{\prime }}+{\rm\Delta}^{\prime })$. Thus the pair
$K_{V}+{\rm\Delta}_{V}=h^{\ast }(K_{Z^{\prime }}+{\rm\Delta}^{\prime })$. Thus the pair 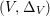 $(V,{\rm\Delta}_{V})$ is klt by [Reference Kollár and MoriKM98, Proposition 5.20]. Moreover,
$(V,{\rm\Delta}_{V})$ is klt by [Reference Kollár and MoriKM98, Proposition 5.20]. Moreover, 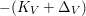 $-(K_{V}+{\rm\Delta}_{V})$ is ample since
$-(K_{V}+{\rm\Delta}_{V})$ is ample since 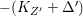 $-(K_{Z^{\prime }}+{\rm\Delta}^{\prime })$ is ample, hence
$-(K_{Z^{\prime }}+{\rm\Delta}^{\prime })$ is ample, hence ![]() $V$ is rationally connected by [Reference Hacon and McKernanHM07, Corollary 1.13]. By [Reference Greb, Kebekus, Kovács and PeternellGKKP11, Theorem 5.1], we have
$V$ is rationally connected by [Reference Hacon and McKernanHM07, Corollary 1.13]. By [Reference Greb, Kebekus, Kovács and PeternellGKKP11, Theorem 5.1], we have 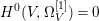 $H^{0}(V,{\rm\Omega}_{V}^{[1]})=0$. However, since general fibers of
$H^{0}(V,{\rm\Omega}_{V}^{[1]})=0$. However, since general fibers of  $W_{0}\rightarrow V_{0}$ are isomorphic to
$W_{0}\rightarrow V_{0}$ are isomorphic to ![]() $\mathbb{P}^{1}$, which does not carry any non-zero pluri-forms, we conclude that
$\mathbb{P}^{1}$, which does not carry any non-zero pluri-forms, we conclude that  $H^{0}(W_{0},{\rm\Omega}_{W_{0}}^{[1]})=\{0\}$ from Lemma 4.9. This is a contradiction.◻
$H^{0}(W_{0},{\rm\Omega}_{W_{0}}^{[1]})=\{0\}$ from Lemma 4.9. This is a contradiction.◻
4.2 Proof of Theorem 1.6
The object of this subsection is to prove Theorem 1.6. We study Mori fibrations ![]() $X\rightarrow Z$ such that
$X\rightarrow Z$ such that ![]() $X$ is a projective threefold with
$X$ is a projective threefold with ![]() $\mathbb{Q}$-factorial canonical singularities and
$\mathbb{Q}$-factorial canonical singularities and ![]() $Z$ is a projective normal surface. Assume that
$Z$ is a projective normal surface. Assume that ![]() $X$ carries non-zero pluri-forms. Then by Theorem 4.2, either the result
$X$ carries non-zero pluri-forms. Then by Theorem 4.2, either the result ![]() $Z^{\prime }$ of any
$Z^{\prime }$ of any 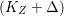 $(K_{Z}+{\rm\Delta})$-MMP has Picard number
$(K_{Z}+{\rm\Delta})$-MMP has Picard number ![]() $2$ or
$2$ or 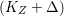 $(K_{Z}+{\rm\Delta})$ is pseudo-effective, where
$(K_{Z}+{\rm\Delta})$ is pseudo-effective, where ![]() ${\rm\Delta}$ is the
${\rm\Delta}$ is the ![]() $\mathbb{Q}$-divisor defined in Theorem 4.2. We study the first case in Proposition 4.10 and the second case in Proposition 4.12.
$\mathbb{Q}$-divisor defined in Theorem 4.2. We study the first case in Proposition 4.10 and the second case in Proposition 4.12.
Proposition 4.10. Let 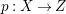 $p:X\rightarrow Z$ be a Mori fibration from a projective threefold to a projective surface such that
$p:X\rightarrow Z$ be a Mori fibration from a projective threefold to a projective surface such that ![]() $X$ has
$X$ has ![]() $\mathbb{Q}$-factorial canonical singularities. Let
$\mathbb{Q}$-factorial canonical singularities. Let ![]() ${\rm\Delta}$ be the divisor in
${\rm\Delta}$ be the divisor in ![]() $Z$ defined in Theorem 4.2. Assume that
$Z$ defined in Theorem 4.2. Assume that 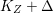 $K_{Z}+{\rm\Delta}$ is not pseudo-effective. Let
$K_{Z}+{\rm\Delta}$ is not pseudo-effective. Let 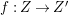 $f:Z\rightarrow Z^{\prime }$ be the result of a
$f:Z\rightarrow Z^{\prime }$ be the result of a 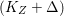 $(K_{Z}+{\rm\Delta})$-MMP, and let
$(K_{Z}+{\rm\Delta})$-MMP, and let ![]() ${\rm\Delta}^{\prime }$ be the strict transform of
${\rm\Delta}^{\prime }$ be the strict transform of ![]() ${\rm\Delta}$ in
${\rm\Delta}$ in ![]() $Z^{\prime }$. Then there is a
$Z^{\prime }$. Then there is a 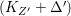 $(K_{Z^{\prime }}+{\rm\Delta}^{\prime })$-Mori fibration
$(K_{Z^{\prime }}+{\rm\Delta}^{\prime })$-Mori fibration 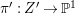 ${\it\pi}^{\prime }:Z^{\prime }\rightarrow \mathbb{P}^{1}$. Let
${\it\pi}^{\prime }:Z^{\prime }\rightarrow \mathbb{P}^{1}$. Let 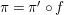 ${\it\pi}={\it\pi}^{\prime }\circ f$, and let
${\it\pi}={\it\pi}^{\prime }\circ f$, and let 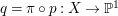 $q={\it\pi}\circ p:X\rightarrow \mathbb{P}^{1}$. Then we have
$q={\it\pi}\circ p:X\rightarrow \mathbb{P}^{1}$. Then we have 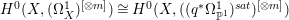 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,((q^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat})^{[\otimes m]})$ for any
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,((q^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat})^{[\otimes m]})$ for any ![]() $m>0$, where
$m>0$, where 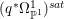 $(q^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat}$ is the saturation of the image of
$(q^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat}$ is the saturation of the image of ![]() $q^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1}$ in
$q^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1}$ in ![]() ${\rm\Omega}_{X}^{[1]}$.
${\rm\Omega}_{X}^{[1]}$.
Proof. Let 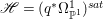 $\mathscr{H}=(q^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat}$, and let
$\mathscr{H}=(q^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat}$, and let 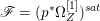 $\mathscr{F}=(p^{\ast }{\rm\Omega}_{Z}^{[1]})^{sat}$. Then we have an exact sequence of coherent sheaves
$\mathscr{F}=(p^{\ast }{\rm\Omega}_{Z}^{[1]})^{sat}$. Then we have an exact sequence of coherent sheaves 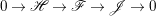 $0\rightarrow \mathscr{H}\rightarrow \mathscr{F}\rightarrow \mathscr{J}\rightarrow 0$, where
$0\rightarrow \mathscr{H}\rightarrow \mathscr{F}\rightarrow \mathscr{J}\rightarrow 0$, where ![]() $\mathscr{J}$ is a torsion-free sheaf such that
$\mathscr{J}$ is a torsion-free sheaf such that 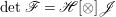 $\text{det}\,\mathscr{F}=\mathscr{H}[\otimes ]\mathscr{J}$. Let
$\text{det}\,\mathscr{F}=\mathscr{H}[\otimes ]\mathscr{J}$. Let ![]() ${\it\alpha}$ be a class of movable curves in
${\it\alpha}$ be a class of movable curves in ![]() $X$ whose image in
$X$ whose image in ![]() $Z$ is not zero and is proportional to the class of general fibers of
$Z$ is not zero and is proportional to the class of general fibers of 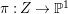 ${\it\pi}:Z\rightarrow \mathbb{P}^{1}$. Then
${\it\pi}:Z\rightarrow \mathbb{P}^{1}$. Then 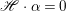 $\mathscr{H}\cdot {\it\alpha}=0$. Moreover, we have
$\mathscr{H}\cdot {\it\alpha}=0$. Moreover, we have
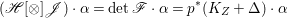 $$\begin{eqnarray}(\mathscr{H}[\otimes ]\mathscr{J})\cdot {\it\alpha}=\text{det}\,\mathscr{F}\cdot {\it\alpha}=p^{\ast }(K_{Z}+{\rm\Delta})\cdot {\it\alpha}\end{eqnarray}$$
$$\begin{eqnarray}(\mathscr{H}[\otimes ]\mathscr{J})\cdot {\it\alpha}=\text{det}\,\mathscr{F}\cdot {\it\alpha}=p^{\ast }(K_{Z}+{\rm\Delta})\cdot {\it\alpha}\end{eqnarray}$$ by Remark 4.5. This intersection number is negative since for a general fiber ![]() $F_{{\it\pi}}$ of
$F_{{\it\pi}}$ of 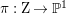 ${\it\pi}:\text{Z}\rightarrow \mathbb{P}^{1}$, we have
${\it\pi}:\text{Z}\rightarrow \mathbb{P}^{1}$, we have 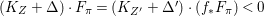 $(K_{Z}+{\rm\Delta})\cdot F_{{\it\pi}}=(K_{Z^{\prime }}+{\rm\Delta}^{\prime })\cdot (f_{\ast }F_{{\it\pi}})<0$. Hence,
$(K_{Z}+{\rm\Delta})\cdot F_{{\it\pi}}=(K_{Z^{\prime }}+{\rm\Delta}^{\prime })\cdot (f_{\ast }F_{{\it\pi}})<0$. Hence, 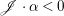 $\mathscr{J}\cdot {\it\alpha}<0$.
$\mathscr{J}\cdot {\it\alpha}<0$.
There is an open subset ![]() $U$ of
$U$ of ![]() $X$ with
$X$ with 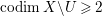 $\text{codim}\,X\setminus U\geqslant 2$ such that we have an exact sequence of locally free sheaves over
$\text{codim}\,X\setminus U\geqslant 2$ such that we have an exact sequence of locally free sheaves over ![]() $U$,
$U$, 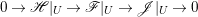 $0\rightarrow \mathscr{H}|_{U}\rightarrow \mathscr{F}|_{U}\rightarrow \mathscr{J}|_{U}\rightarrow 0$. Since
$0\rightarrow \mathscr{H}|_{U}\rightarrow \mathscr{F}|_{U}\rightarrow \mathscr{J}|_{U}\rightarrow 0$. Since 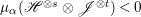 ${\it\mu}_{{\it\alpha}}(\mathscr{H}^{\otimes s}\otimes \mathscr{J}^{\otimes t})<0$ if
${\it\mu}_{{\it\alpha}}(\mathscr{H}^{\otimes s}\otimes \mathscr{J}^{\otimes t})<0$ if ![]() $t>0$, we have
$t>0$, we have 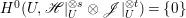 $H^{0}(U,\mathscr{H}|_{U}^{\otimes s}\otimes \mathscr{J}|_{U}^{\otimes t})=\{0\}$ if
$H^{0}(U,\mathscr{H}|_{U}^{\otimes s}\otimes \mathscr{J}|_{U}^{\otimes t})=\{0\}$ if ![]() $t>0$ by Proposition 2.1. Hence, by Lemmas 2.5 and 2.4, we have
$t>0$ by Proposition 2.1. Hence, by Lemmas 2.5 and 2.4, we have 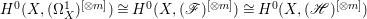 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,(\mathscr{F})^{[\otimes m]})\cong H^{0}(X,(\mathscr{H})^{[\otimes m]})$ for any
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\cong H^{0}(X,(\mathscr{F})^{[\otimes m]})\cong H^{0}(X,(\mathscr{H})^{[\otimes m]})$ for any ![]() $m>0$.◻
$m>0$.◻
Example 4.11. We give an example of this kind of threefold. Let 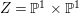 $Z=\mathbb{P}^{1}\times \mathbb{P}^{1}$. Denote by
$Z=\mathbb{P}^{1}\times \mathbb{P}^{1}$. Denote by ![]() $p_{1}$,
$p_{1}$, ![]() $p_{2}$ the two natural projections from
$p_{2}$ the two natural projections from ![]() $Z$ to
$Z$ to ![]() $\mathbb{P}^{1}$. Let
$\mathbb{P}^{1}$. Let 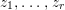 $z_{1},\ldots ,z_{r}$ be
$z_{1},\ldots ,z_{r}$ be ![]() $r\geqslant 4$ different points in
$r\geqslant 4$ different points in ![]() $\mathbb{P}^{1}$, and let
$\mathbb{P}^{1}$, and let 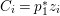 $C_{i}=p_{1}^{\ast }z_{i}$ for
$C_{i}=p_{1}^{\ast }z_{i}$ for 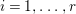 $i=1,\ldots ,r$. Let
$i=1,\ldots ,r$. Let 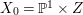 $X_{0}=\mathbb{P}^{1}\times Z$. By the method of Construction 2.13, we can construct a Mori fibration
$X_{0}=\mathbb{P}^{1}\times Z$. By the method of Construction 2.13, we can construct a Mori fibration 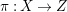 ${\it\pi}:X\rightarrow Z$ such that
${\it\pi}:X\rightarrow Z$ such that 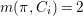 $m({\it\pi},C_{i})=2$ for
$m({\it\pi},C_{i})=2$ for 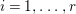 $i=1,\ldots ,r$. Note that
$i=1,\ldots ,r$. Note that 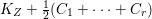 $K_{Z}+\frac{1}{2}(C_{1}+\cdots +C_{r})$ is not pseudo-effective since it has negative intersection number with general fibers of
$K_{Z}+\frac{1}{2}(C_{1}+\cdots +C_{r})$ is not pseudo-effective since it has negative intersection number with general fibers of ![]() $p_{1}$. Moreover, we have
$p_{1}$. Moreover, we have
 $$\begin{eqnarray}\displaystyle H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes 2]}) & \cong & \displaystyle H^{0}(\mathbb{P}^{1},({\rm\Omega}_{\mathbb{P}^{1}}^{1})^{\otimes 2}\otimes \mathscr{O}_{\mathbb{P}^{1}}(C_{1}+\cdots +C_{r}))\nonumber\\ \displaystyle & \cong & \displaystyle H^{0}(\mathbb{P}^{1},\mathscr{O}_{\mathbb{P}^{1}}(-4+r))\neq \{0\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes 2]}) & \cong & \displaystyle H^{0}(\mathbb{P}^{1},({\rm\Omega}_{\mathbb{P}^{1}}^{1})^{\otimes 2}\otimes \mathscr{O}_{\mathbb{P}^{1}}(C_{1}+\cdots +C_{r}))\nonumber\\ \displaystyle & \cong & \displaystyle H^{0}(\mathbb{P}^{1},\mathscr{O}_{\mathbb{P}^{1}}(-4+r))\neq \{0\}.\nonumber\end{eqnarray}$$Now we treat the second case. Note that this is the case for Examples 2.12 and 2.14.
Proposition 4.12. Let 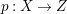 $p:X\rightarrow Z$ be a Mori fibration from a projective threefold to a projective surface. Assume that
$p:X\rightarrow Z$ be a Mori fibration from a projective threefold to a projective surface. Assume that ![]() $X$ has
$X$ has ![]() $\mathbb{Q}$-factorial klt singularities. Assume that
$\mathbb{Q}$-factorial klt singularities. Assume that 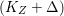 $(K_{Z}+{\rm\Delta})$ is pseudo-effective, where
$(K_{Z}+{\rm\Delta})$ is pseudo-effective, where ![]() ${\rm\Delta}$ is the
${\rm\Delta}$ is the ![]() $\mathbb{Q}$-divisor defined in Theorem 4.2. Then
$\mathbb{Q}$-divisor defined in Theorem 4.2. Then ![]() $X$ carries non-zero pluri-forms.
$X$ carries non-zero pluri-forms.
Proof. By the abundance theorem for log surfaces (see [Reference Abramovich, Fong, Kollár and McKernanAFKM92, Theorem 11.1.3]), 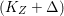 $(K_{Z}+{\rm\Delta})$ is
$(K_{Z}+{\rm\Delta})$ is ![]() $\mathbb{Q}$-effective. Hence, there is a positive integer
$\mathbb{Q}$-effective. Hence, there is a positive integer ![]() $l$ such that
$l$ such that 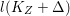 $l(K_{Z}+{\rm\Delta})$ is an effective Cartier divisor. This implies that
$l(K_{Z}+{\rm\Delta})$ is an effective Cartier divisor. This implies that 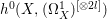 $h^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes 2l]})$ is non-zero by Lemma 4.4.◻
$h^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes 2l]})$ is non-zero by Lemma 4.4.◻
We can now conclude Theorem 1.6.
Proof of Theorem 1.6.
Let 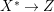 $X^{\ast }\rightarrow Z$ be a Mori fibration. If
$X^{\ast }\rightarrow Z$ be a Mori fibration. If ![]() $Z$ is a curve, then we are in the second case of the theorem. Assume that
$Z$ is a curve, then we are in the second case of the theorem. Assume that 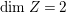 $\text{dim}\,Z=2$. If
$\text{dim}\,Z=2$. If 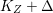 $K_{Z}+{\rm\Delta}$ is
$K_{Z}+{\rm\Delta}$ is ![]() $\mathbb{Q}$-effective, then we are in the situation of Proposition 4.12. If
$\mathbb{Q}$-effective, then we are in the situation of Proposition 4.12. If 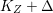 $K_{Z}+{\rm\Delta}$ is not
$K_{Z}+{\rm\Delta}$ is not ![]() $\mathbb{Q}$-effective, then by Proposition 4.10, there is a fibration
$\mathbb{Q}$-effective, then by Proposition 4.10, there is a fibration 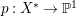 $p:X^{\ast }\rightarrow \mathbb{P}^{1}$ such that
$p:X^{\ast }\rightarrow \mathbb{P}^{1}$ such that 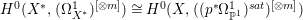 $H^{0}(X^{\ast },({\rm\Omega}_{X^{\ast }}^{1})^{[\otimes m]})\cong H^{0}(X,((p^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat})^{[\otimes m]})$ for any
$H^{0}(X^{\ast },({\rm\Omega}_{X^{\ast }}^{1})^{[\otimes m]})\cong H^{0}(X,((p^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat})^{[\otimes m]})$ for any ![]() $m>0$. By Lemma 3.1, we have
$m>0$. By Lemma 3.1, we have 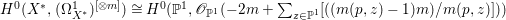 $H^{0}(X^{\ast },({\rm\Omega}_{X^{\ast }}^{1})^{[\otimes m]})\cong H^{0}(\mathbb{P}^{1},\mathscr{O}_{\mathbb{P}^{1}}(-2m+\sum _{z\in \mathbb{P}^{1}}[((m(p,z)-1)m)/m(p,z)]))$ for any
$H^{0}(X^{\ast },({\rm\Omega}_{X^{\ast }}^{1})^{[\otimes m]})\cong H^{0}(\mathbb{P}^{1},\mathscr{O}_{\mathbb{P}^{1}}(-2m+\sum _{z\in \mathbb{P}^{1}}[((m(p,z)-1)m)/m(p,z)]))$ for any ![]() $m>0$.◻
$m>0$.◻
5 Proof of Theorem 1.4
In this section, we complete the proof of Theorem 1.4. First, we show that if ![]() $X$ is a rationally connected projective threefold with
$X$ is a rationally connected projective threefold with ![]() $\mathbb{Q}$-factorial terminal singularities, which carries non-zero pluri-forms, then there is a dominant rational map from
$\mathbb{Q}$-factorial terminal singularities, which carries non-zero pluri-forms, then there is a dominant rational map from ![]() $X$ to
$X$ to ![]() $\mathbb{P}^{1}$ (Lemma 5.2). To this end, we need the following lemma.
$\mathbb{P}^{1}$ (Lemma 5.2). To this end, we need the following lemma.
Lemma 5.1. Let 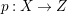 $p:X\rightarrow Z$ be a Mori fibration such that
$p:X\rightarrow Z$ be a Mori fibration such that ![]() $X$ has
$X$ has ![]() $\mathbb{Q}$-factorial terminal singularities and
$\mathbb{Q}$-factorial terminal singularities and 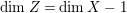 $\text{dim}\,Z=\text{dim}\,X-1$. Then there exists an open subset
$\text{dim}\,Z=\text{dim}\,X-1$. Then there exists an open subset ![]() $Z_{0}\subseteq Z$ with
$Z_{0}\subseteq Z$ with 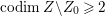 $\text{codim}\,Z\setminus Z_{0}\geqslant 2$ such that every scheme-theoretic fiber over
$\text{codim}\,Z\setminus Z_{0}\geqslant 2$ such that every scheme-theoretic fiber over ![]() $Z_{0}$ is reduced.
$Z_{0}$ is reduced.
Proof. By taking general hyperplane sections on ![]() $Z$, we reduce to the case where
$Z$, we reduce to the case where ![]() $Z$ is a smooth curve and
$Z$ is a smooth curve and ![]() $p$ is a Fano fibration. In this case,
$p$ is a Fano fibration. In this case, ![]() $X$ is a surface with terminal singularities. Hence,
$X$ is a surface with terminal singularities. Hence, ![]() $X$ is smooth and the fibers of
$X$ is smooth and the fibers of ![]() $p$ are reduced.◻
$p$ are reduced.◻
Lemma 5.2. Let ![]() $X$ be a rationally connected projective threefold with
$X$ be a rationally connected projective threefold with ![]() $\mathbb{Q}$-factorial terminal singularities such that
$\mathbb{Q}$-factorial terminal singularities such that 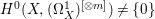 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some ![]() $m>0$. Let
$m>0$. Let 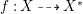 $f:X{\dashrightarrow}X^{\ast }$ be the result of an MMP for
$f:X{\dashrightarrow}X^{\ast }$ be the result of an MMP for ![]() $X$. Then there is a fibration
$X$. Then there is a fibration 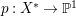 $p:X^{\ast }\rightarrow \mathbb{P}^{1}$.
$p:X^{\ast }\rightarrow \mathbb{P}^{1}$.
Proof. Note that ![]() $X^{\ast }$ is a Mori fiber space. Then we have a Mori fibration
$X^{\ast }$ is a Mori fiber space. Then we have a Mori fibration 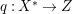 $q:X^{\ast }\rightarrow Z$, where
$q:X^{\ast }\rightarrow Z$, where ![]() $Z$ is a normal rationally connected variety. If
$Z$ is a normal rationally connected variety. If 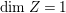 $\text{dim}\,Z=1$, then we are done.
$\text{dim}\,Z=1$, then we are done.
By Lemma 2.2, we know that ![]() $X^{\ast }$ carries non-zero pluri-forms. Hence,
$X^{\ast }$ carries non-zero pluri-forms. Hence, 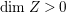 $\text{dim}\,Z>0$ by [Reference OuOu14, Theorem 3.1]. Assume that
$\text{dim}\,Z>0$ by [Reference OuOu14, Theorem 3.1]. Assume that 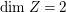 $\text{dim}\,Z=2$. Then
$\text{dim}\,Z=2$. Then ![]() $Z$ has canonical singularities by [Reference Mori and ProkhorovMP08, Corollary 1.2.8]. Hence,
$Z$ has canonical singularities by [Reference Mori and ProkhorovMP08, Corollary 1.2.8]. Hence, ![]() $K_{Z}$ is not pseudo-effective by [Reference KollárKol96, Corollary 1.11]. Moreover, by Lemma 5.1,
$K_{Z}$ is not pseudo-effective by [Reference KollárKol96, Corollary 1.11]. Moreover, by Lemma 5.1, 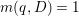 $m(q,D)=1$ for any effective divisor
$m(q,D)=1$ for any effective divisor ![]() $D$ on
$D$ on ![]() $Z$. Hence, by Theorem 4.2, if
$Z$. Hence, by Theorem 4.2, if ![]() $Z\rightarrow Z^{\prime }$ is the result of an MMP for
$Z\rightarrow Z^{\prime }$ is the result of an MMP for ![]() $Z$, then
$Z$, then ![]() $Z^{\prime }$ has Picard number
$Z^{\prime }$ has Picard number ![]() $2$. Hence, we have a Mori fibration
$2$. Hence, we have a Mori fibration 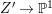 $Z^{\prime }\rightarrow \mathbb{P}^{1}$. Let
$Z^{\prime }\rightarrow \mathbb{P}^{1}$. Let ![]() $p$ be the composition of
$p$ be the composition of 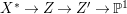 $X^{\ast }\rightarrow Z\rightarrow Z^{\prime }\rightarrow \mathbb{P}^{1}$. Then
$X^{\ast }\rightarrow Z\rightarrow Z^{\prime }\rightarrow \mathbb{P}^{1}$. Then ![]() $p$ is a fibration from
$p$ is a fibration from ![]() $X^{\ast }$ to
$X^{\ast }$ to ![]() $\mathbb{P}^{1}$ ◻
$\mathbb{P}^{1}$ ◻
With the notation as above, note that a general fiber ![]() $F^{\prime }$ of
$F^{\prime }$ of 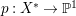 $p:X^{\ast }\rightarrow \mathbb{P}^{1}$ is a smooth rationally connected surface. Hence,
$p:X^{\ast }\rightarrow \mathbb{P}^{1}$ is a smooth rationally connected surface. Hence, ![]() $F^{\prime }$ does not carry any non-zero pluri-forms. Let
$F^{\prime }$ does not carry any non-zero pluri-forms. Let ![]() $U$ be the largest open subset in
$U$ be the largest open subset in ![]() $X$ over which
$X$ over which 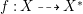 $f:X{\dashrightarrow}X^{\ast }$ is regular. Then
$f:X{\dashrightarrow}X^{\ast }$ is regular. Then 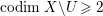 $\text{codim}\,X\setminus U\geqslant 2$,
$\text{codim}\,X\setminus U\geqslant 2$, 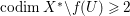 $\text{codim}\,X^{\ast }\setminus f(U)\geqslant 2$, and the rational map
$\text{codim}\,X^{\ast }\setminus f(U)\geqslant 2$, and the rational map 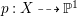 $p:X{\dashrightarrow}\mathbb{P}^{1}$ is regular over
$p:X{\dashrightarrow}\mathbb{P}^{1}$ is regular over ![]() $U$. If
$U$. If ![]() $F$ is a general fiber of
$F$ is a general fiber of ![]() $U\rightarrow \mathbb{P}^{1}$, then
$U\rightarrow \mathbb{P}^{1}$, then 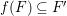 $f(F)\subseteq F^{\prime }$, where
$f(F)\subseteq F^{\prime }$, where ![]() $F^{\prime }$ is a general fiber of
$F^{\prime }$ is a general fiber of ![]() $p$. Moreover,
$p$. Moreover, 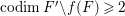 $\text{codim}\,F^{\prime }\setminus f(F)\geqslant 2$. Hence,
$\text{codim}\,F^{\prime }\setminus f(F)\geqslant 2$. Hence, ![]() $f(F)$ does not carry any non-zero pluri-forms and neither does
$f(F)$ does not carry any non-zero pluri-forms and neither does ![]() $F$ by Lemma 2.2. The following lemma shows that the rational map
$F$ by Lemma 2.2. The following lemma shows that the rational map 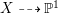 $X{\dashrightarrow}\mathbb{P}^{1}$ is regular. Moreover, general fibers of
$X{\dashrightarrow}\mathbb{P}^{1}$ is regular. Moreover, general fibers of 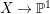 $X\rightarrow \mathbb{P}^{1}$ are birational to the ones of
$X\rightarrow \mathbb{P}^{1}$ are birational to the ones of 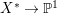 $X^{\ast }\rightarrow \mathbb{P}^{1}$ which are rationally connected. Hence, general fibers of
$X^{\ast }\rightarrow \mathbb{P}^{1}$ which are rationally connected. Hence, general fibers of 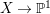 $X\rightarrow \mathbb{P}^{1}$ are rationally connected.
$X\rightarrow \mathbb{P}^{1}$ are rationally connected.
Lemma 5.3. Let ![]() $X$ be a projective threefold with
$X$ be a projective threefold with ![]() $\mathbb{Q}$-factorial terminal singularities. Assume that there is a non-constant rational map
$\mathbb{Q}$-factorial terminal singularities. Assume that there is a non-constant rational map 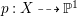 $p:X{\dashrightarrow}\mathbb{P}^{1}$ which is regular over
$p:X{\dashrightarrow}\mathbb{P}^{1}$ which is regular over ![]() $U$ such that
$U$ such that 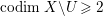 $\text{codim}\,X\setminus U\geqslant 2$. Assume that general fibers of
$\text{codim}\,X\setminus U\geqslant 2$. Assume that general fibers of ![]() $U\rightarrow \mathbb{P}^{1}$ do not carry any pluri-forms. If
$U\rightarrow \mathbb{P}^{1}$ do not carry any pluri-forms. If 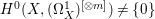 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})\neq \{0\}$ for some ![]() $m>0$, then
$m>0$, then ![]() $p$ is regular.
$p$ is regular.
Proof. Let ![]() ${\rm\Gamma}$ be the normalization of the graph of
${\rm\Gamma}$ be the normalization of the graph of ![]() $p$. Let
$p$. Let 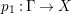 $p_{1}:{\rm\Gamma}\rightarrow X$,
$p_{1}:{\rm\Gamma}\rightarrow X$, 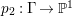 $p_{2}:{\rm\Gamma}\rightarrow \mathbb{P}^{1}$ be the natural projections. Then there is a natural injection from
$p_{2}:{\rm\Gamma}\rightarrow \mathbb{P}^{1}$ be the natural projections. Then there is a natural injection from 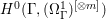 $H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})$ to
$H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})$ to 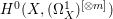 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ by Lemma 2.2. Let
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ by Lemma 2.2. Let ![]() ${\it\sigma}$ be a non-zero element in
${\it\sigma}$ be a non-zero element in 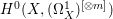 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$. Then
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$. Then ![]() ${\it\sigma}$ induces a rational section
${\it\sigma}$ induces a rational section ![]() ${\it\sigma}_{{\rm\Gamma}}$ of
${\it\sigma}_{{\rm\Gamma}}$ of 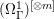 $({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]}$ on
$({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]}$ on ![]() ${\rm\Gamma}$. Let
${\rm\Gamma}$. Let ![]() $E$ be a
$E$ be a ![]() $p_{1}$-exceptional divisor. Then there is a curve in
$p_{1}$-exceptional divisor. Then there is a curve in ![]() $E$ which is contracted by
$E$ which is contracted by ![]() $p_{2}$ since
$p_{2}$ since 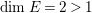 $\text{dim}\,E=2>1$. Hence, this curve is not contracted by
$\text{dim}\,E=2>1$. Hence, this curve is not contracted by ![]() $p_{1}$ since the graph of
$p_{1}$ since the graph of ![]() $p$ is included in
$p$ is included in ![]() $X\times \mathbb{P}^{1}$ and the normalization map is finite. Thus,
$X\times \mathbb{P}^{1}$ and the normalization map is finite. Thus, ![]() $p_{1}(E)$ is a curve in
$p_{1}(E)$ is a curve in ![]() $X$, and
$X$, and ![]() $X$ is smooth around the generic point of
$X$ is smooth around the generic point of ![]() $p_{1}(E)$ since
$p_{1}(E)$ since ![]() $X$ is smooth in codimension
$X$ is smooth in codimension ![]() $2$ (see [Reference Kollár and MoriKM98, Corollary 5.18]). Hence,
$2$ (see [Reference Kollár and MoriKM98, Corollary 5.18]). Hence, ![]() ${\it\sigma}_{{\rm\Gamma}}$ does not have a pole along
${\it\sigma}_{{\rm\Gamma}}$ does not have a pole along ![]() $E$. This implies that we have an isomorphism from
$E$. This implies that we have an isomorphism from 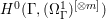 $H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})$ to
$H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})$ to 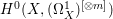 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ induced by
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$ induced by ![]() $p_{1}$.
$p_{1}$.
Note that ![]() $p_{1}^{-1}|_{U}$ induces an isomorphism from
$p_{1}^{-1}|_{U}$ induces an isomorphism from ![]() $U$ onto its image. If
$U$ onto its image. If ![]() $F_{U}$ is the fiber of
$F_{U}$ is the fiber of ![]() $p|_{U}$ over a general point
$p|_{U}$ over a general point ![]() $z$, then
$z$, then 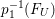 $p_{1}^{-1}(F_{U})$ is an open subset of
$p_{1}^{-1}(F_{U})$ is an open subset of ![]() $F_{{\rm\Gamma}}$, where
$F_{{\rm\Gamma}}$, where ![]() $F_{{\rm\Gamma}}$ is the fiber of
$F_{{\rm\Gamma}}$ is the fiber of 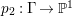 $p_{2}:{\rm\Gamma}\rightarrow \mathbb{P}^{1}$ over
$p_{2}:{\rm\Gamma}\rightarrow \mathbb{P}^{1}$ over ![]() $z$. Since
$z$. Since ![]() $F_{U}$ does not carry any non-zero pluri-forms, neither does
$F_{U}$ does not carry any non-zero pluri-forms, neither does ![]() $F_{{\rm\Gamma}}$. By Lemma 2.5, this implies that
$F_{{\rm\Gamma}}$. By Lemma 2.5, this implies that 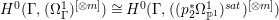 $H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})\cong H^{0}({\rm\Gamma},((p_{2}^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat})^{[\otimes m]})$.
$H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})\cong H^{0}({\rm\Gamma},((p_{2}^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat})^{[\otimes m]})$.
We first prove that ![]() $p$ is regular in codimension
$p$ is regular in codimension ![]() $2$. Assume the opposite. Then there is a divisor
$2$. Assume the opposite. Then there is a divisor ![]() $D$ in
$D$ in ![]() ${\rm\Gamma}$ which is exceptional for
${\rm\Gamma}$ which is exceptional for 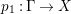 $p_{1}:{\rm\Gamma}\rightarrow X$, and the codimension of
$p_{1}:{\rm\Gamma}\rightarrow X$, and the codimension of ![]() $p_{1}(D)$ in
$p_{1}(D)$ in ![]() $X$ is
$X$ is ![]() $2$. Since
$2$. Since ![]() $X$ is smooth in codimension
$X$ is smooth in codimension ![]() $2$ (see [Reference Kollár and MoriKM98, Corollary 5.18]),
$2$ (see [Reference Kollár and MoriKM98, Corollary 5.18]), ![]() $X$ is smooth around the generic point of
$X$ is smooth around the generic point of ![]() $p_{1}(D)$. Thus, there is a smooth quasi-projective curve
$p_{1}(D)$. Thus, there is a smooth quasi-projective curve ![]() $C$ in
$C$ in ![]() $D$ such that
$D$ such that ![]() ${\rm\Gamma}$ is smooth along
${\rm\Gamma}$ is smooth along ![]() $C$ and
$C$ and ![]() $C$ is contracted to a smooth point of
$C$ is contracted to a smooth point of ![]() $X$ by
$X$ by ![]() $p_{1}$. Note that
$p_{1}$. Note that ![]() $C$ is horizontal over
$C$ is horizontal over ![]() $\mathbb{P}^{1}$ under the projection
$\mathbb{P}^{1}$ under the projection 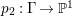 $p_{2}:{\rm\Gamma}\rightarrow \mathbb{P}^{1}$ for the same reason as before. Let
$p_{2}:{\rm\Gamma}\rightarrow \mathbb{P}^{1}$ for the same reason as before. Let ![]() ${\it\sigma}$ be a non-zero element in
${\it\sigma}$ be a non-zero element in 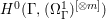 $H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})$. By the exact sequence of locally free sheaves
$H^{0}({\rm\Gamma},({\rm\Omega}_{{\rm\Gamma}}^{1})^{[\otimes m]})$. By the exact sequence of locally free sheaves 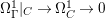 ${\rm\Omega}_{{\rm\Gamma}}^{1}|_{C}\rightarrow {\rm\Omega}_{C}^{1}\rightarrow 0$,
${\rm\Omega}_{{\rm\Gamma}}^{1}|_{C}\rightarrow {\rm\Omega}_{C}^{1}\rightarrow 0$, ![]() ${\it\sigma}$ induce an element
${\it\sigma}$ induce an element ![]() ${\it\sigma}_{C}$ in
${\it\sigma}_{C}$ in 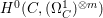 $H^{0}(C,({\rm\Omega}_{C}^{1})^{\otimes m})$. On the one hand,
$H^{0}(C,({\rm\Omega}_{C}^{1})^{\otimes m})$. On the one hand, ![]() $C$ is horizontal over
$C$ is horizontal over ![]() $\mathbb{P}^{1}$ and
$\mathbb{P}^{1}$ and ![]() ${\it\sigma}$ is non-zero in
${\it\sigma}$ is non-zero in 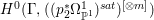 $H^{0}({\rm\Gamma},((p_{2}^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat})^{[\otimes m]})$, we have
$H^{0}({\rm\Gamma},((p_{2}^{\ast }{\rm\Omega}_{\mathbb{P}^{1}}^{1})^{sat})^{[\otimes m]})$, we have ![]() ${\it\sigma}_{C}\neq 0$. On the other hand, since
${\it\sigma}_{C}\neq 0$. On the other hand, since ![]() $C$ is contracted to a smooth point in
$C$ is contracted to a smooth point in ![]() $X$, we obtain
$X$, we obtain ![]() ${\it\sigma}_{C}=0$ for
${\it\sigma}_{C}=0$ for ![]() ${\it\sigma}$ is the pullback of certain element in
${\it\sigma}$ is the pullback of certain element in 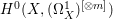 $H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$. This is a contradiction.
$H^{0}(X,({\rm\Omega}_{X}^{1})^{[\otimes m]})$. This is a contradiction.
Now we prove that ![]() $p$ is regular. Let
$p$ is regular. Let ![]() $F_{1}$ and
$F_{1}$ and ![]() $F_{2}$ be two different fibers of
$F_{2}$ be two different fibers of ![]() $U\rightarrow \mathbb{P}^{1}$. Then their closures in
$U\rightarrow \mathbb{P}^{1}$. Then their closures in ![]() $X$ are two Weil divisors and their intersection is included in a closed subset of codimension at most
$X$ are two Weil divisors and their intersection is included in a closed subset of codimension at most ![]() $3$. Hence, their intersection is empty since
$3$. Hence, their intersection is empty since ![]() $X$ is
$X$ is ![]() $\mathbb{Q}$-factorial. This implies that
$\mathbb{Q}$-factorial. This implies that ![]() $p$ is regular.◻
$p$ is regular.◻
Together with Lemmas 2.5 and 3.1, we can conclude Theorem 1.4.
Proof of Theorem 1.4.
By Lemmas 5.2 and 5.3, there is a fibration 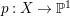 $p:X\rightarrow \mathbb{P}^{1}$ such that general fibers of
$p:X\rightarrow \mathbb{P}^{1}$ such that general fibers of ![]() $p$ do not carry any non-zero pluri-forms. Lemma 2.5 shows that all pluri-forms on
$p$ do not carry any non-zero pluri-forms. Lemma 2.5 shows that all pluri-forms on ![]() $X$ come from the base
$X$ come from the base ![]() $\mathbb{P}^{1}$. Finally, we obtain the formula in the theorem from Lemma 3.1.◻
$\mathbb{P}^{1}$. Finally, we obtain the formula in the theorem from Lemma 3.1.◻
Acknowledgments
The author would like to thank his advisor Stéphane Druel for suggesting this question and for his help. He would also like to thank the referee for the numerous comments and remarks.