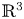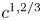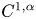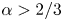1. Introduction
1.1. Background
It often happens, in differential geometry, as in other contexts where nonlinear PDEs appear, that the solutions to a given nonlinear system of equations satisfy also systems of higher order equations carrying significant geometric or analytic information. A very basic example is the Gauss–Codazzi–Mainardi equations satisfied by any smooth isometric immersion of a two-dimensional Riemannian manifold into ${\mathbb {R}}^3$![]() . Note that, in their turn, these equations can be used to prove certain rigidity statements for the immersion, e.g. to show that any isometric immersion of a flat domain is developable, i.e. roughly speaking, at any given point $p$
. Note that, in their turn, these equations can be used to prove certain rigidity statements for the immersion, e.g. to show that any isometric immersion of a flat domain is developable, i.e. roughly speaking, at any given point $p$![]() its image contains a segment of ${\mathbb {R}}^3$
its image contains a segment of ${\mathbb {R}}^3$![]() passing through $p$
passing through $p$![]() .
.
The subtlety which is often glossed over in the context of classical differential geometry, where all the mappings are assumed smooth, or at least twice or thrice continuously differentiable, is that, due to nonlinearity, the passage from say a given set of first order equations, e.g. the system of isometric immersion equations in our example, to the higher order equations requires a minimum of regularity. There is no guarantee that in the absence of this regularity the geometric information hidden in the higher order equations would be accessible. The above mentioned subtlety could be a source of confusion. Coming back to our example, it is often assumed that all isometric images of flat domains must be ruled, which is untrue. Already, at the dawn of modern differential geometry, no less figures than Lebesgue and Picard intuited the existence of a surface which could be flattened onto the plane with no distortion of relative distances, but nowhere contained a straight segment. To quote PicardFootnote 1:
According to general practice, we suppose in the preceding analysis, as in all infinitesimal geometry of curves and surfaces, the existence of derivatives which we need in the calculus. It may seem premature to entertain a theory of surfaces in which one does not make such hypotheses. However, a curious result has been pointed out by Mr Lebesgue (Comptes Rendus, 1899 and thesis)Footnote 2 ; according to which one may, by the aid of continuous functions, obtain surfaces corresponding to a plane, of such sort that every rectifiable line of the plane has a corresponding rectifiable line of the same length of the surface, nevertheless the surfaces obtained are no longer ruled. If one takes a sheet of paper, and crumples it by hand, one obtains a surface applicable to the plane and made up of a finite number of pieces of developable surfaces, joined two and two by lines, along which they form a certain angle. If one imagines that the pieces become infinitely small, the crumpling being pushed everywhere to the limit, one may arrive at the conception of surfaces applicable to the plane and yet not developable [in the sense that there is no envelope of a family of planes of one parameter and not ruled].
The suggested constructions by Lebesgue and then Picard fall short of being totally satisfactory as they point to continuous but yet not differentiable mappings. However, they were perhaps the heralds of a celebrated result due to Kuiper [Reference Kuiper39], who based on the work by John Nash [Reference Nash47, Reference Nash48] proved that any Riemannian manifold can be $C^1$![]() isometrically embedded into a Riemannian manifold of one dimension higher. (Actually, by Nash and Kuiper's construction, $C^1$
isometrically embedded into a Riemannian manifold of one dimension higher. (Actually, by Nash and Kuiper's construction, $C^1$![]() isometric embeddings can approximate any short immersion.) As a consequence, the flat disk can be $C^1$
isometric embeddings can approximate any short immersion.) As a consequence, the flat disk can be $C^1$![]() -isometrically embedded into any given small ball of ${\mathbb {R}}^3$
-isometrically embedded into any given small ball of ${\mathbb {R}}^3$![]() and hence the image cannot be ruled. To make the matters worse, these embeddings can be made through recurrent self-similar corrugations [Reference Borrelli, Jabrane, Lazarus and Thibert3, Reference Borrelli, Jabrane, Lazarus and Thibert4], whose images seem, without a proof at hand, not to include any straight segment of ${\mathbb {R}}^3$
and hence the image cannot be ruled. To make the matters worse, these embeddings can be made through recurrent self-similar corrugations [Reference Borrelli, Jabrane, Lazarus and Thibert3, Reference Borrelli, Jabrane, Lazarus and Thibert4], whose images seem, without a proof at hand, not to include any straight segment of ${\mathbb {R}}^3$![]() in any scale. In contrast, and returning to our original developability statement in a higher regularity setting where the Gauss–Codazzi equations hold true, Hartman and Nirenberg [Reference Hartman and Nirenberg28] proved, incidentally almost at the same time Nash and Kuiper showcased their results, that a $C^2$
in any scale. In contrast, and returning to our original developability statement in a higher regularity setting where the Gauss–Codazzi equations hold true, Hartman and Nirenberg [Reference Hartman and Nirenberg28] proved, incidentally almost at the same time Nash and Kuiper showcased their results, that a $C^2$![]() -regular isometric immersion of a flat domain must have a locally ruled surface as its image. We have come full circle, and this discussed dichotomy leaves us with a fundamental question any analyst would like to ask: At what regularity threshold or thresholds between $C^1$
-regular isometric immersion of a flat domain must have a locally ruled surface as its image. We have come full circle, and this discussed dichotomy leaves us with a fundamental question any analyst would like to ask: At what regularity threshold or thresholds between $C^1$![]() and $C^2$
and $C^2$![]() the unruled isometries transition into the ruled regime?
the unruled isometries transition into the ruled regime?
1.2. Recent developments
To put the problem described above in a broader context, we note that the above dichotomy—known in the recent literature as flexibility vs. rigidity—is not specific to the case of isometric immersions. The Nash and Kuiper scheme for creating highly oscillatory anomalous solutions of typically lower regularity through iterations could be studied under the broader topic of convex integration [Reference Gromov25, Reference Spring54] for the differential inclusions (or PDEs re-cast in this framework), and the involved density or flexibility-related results are usually referred to as h-principle. The existence of such h-principle is usually accompanied by a parallel rigidity property which indicates that the construction cannot be carried out in high regularity scales. A notable example is the recent discovery by the first author and Székelyhidi [Reference De Lellis and Székelyhidi17]: They showed that the system of Euler equations in fluid dynamics is given to the convex integration method and that Nash and Kuiper's iterations can be adapted in this case in order to create non-conservative compactly supported continuous flows approximating an open set of subsolutions (see [Reference De Lellis and Székelyhidi18, Reference Székelyhidi55] for a thorough discussion of the connection between the two problems of turbulence and isometric immersions). Their results, and the subsequent work in improving the regularity of the anomalous solutions stood in contrast with the rigidity result reflected in the conservation of energy for solutions passing a certain regularity threshold ($\alpha >1/3$![]() for $C^{1,\alpha }$
for $C^{1,\alpha }$![]() -Hölder continuous solutions) in [Reference Constantin and Titi12, Reference Eyink20], as conjectured by Onsager [Reference Onsager49]. Their approach finally lead to the complete resolution of this conjecture by Isett in [Reference Isett31]; see [Reference De Lellis and Székelyhidi19] for a review of the history of the problem and the intermediate results.
-Hölder continuous solutions) in [Reference Constantin and Titi12, Reference Eyink20], as conjectured by Onsager [Reference Onsager49]. Their approach finally lead to the complete resolution of this conjecture by Isett in [Reference Isett31]; see [Reference De Lellis and Székelyhidi19] for a review of the history of the problem and the intermediate results.
Coming back to the question of isometric immersions, a parallel question is whether the images of isometric immersions into ${\mathbb {R}}^3$![]() of closed convex surfaces (i.e. $2$
of closed convex surfaces (i.e. $2$![]() -manifolds with no boundary and positive Gaussian curvature) are rigid motions. This result follows from the convexity of the image of such surfaces. This convexity fails for $C^{1,\alpha }$
-manifolds with no boundary and positive Gaussian curvature) are rigid motions. This result follows from the convexity of the image of such surfaces. This convexity fails for $C^{1,\alpha }$![]() isometric immersions of convex surfaces if $\alpha <1/5$
isometric immersions of convex surfaces if $\alpha <1/5$![]() , in which regime the above mentioned h-principle for isometric immersions holds true, as shown in [Reference Cao and Székelyhidi9, Reference De Lellis, Inauen and Székelyhidi16], improving on the results by [Reference Borisov6, Reference Conti, De Lellis and Székelyhidi13]. On the other hand, following Borisov [Reference Borisov5], Conti et al. proved in [Reference Conti, De Lellis and Székelyhidi13, Reference Conti, De Lellis and Székelyhidi14] that when $\alpha >2/3$
, in which regime the above mentioned h-principle for isometric immersions holds true, as shown in [Reference Cao and Székelyhidi9, Reference De Lellis, Inauen and Székelyhidi16], improving on the results by [Reference Borisov6, Reference Conti, De Lellis and Székelyhidi13]. On the other hand, following Borisov [Reference Borisov5], Conti et al. proved in [Reference Conti, De Lellis and Székelyhidi13, Reference Conti, De Lellis and Székelyhidi14] that when $\alpha >2/3$![]() , the isometric image of a closed convex surface is convex (from which it follows that the immersion is a rigid motion), and that more generally the h-principle cannot hold true for isometric immersions of any elliptic $2$
, the isometric image of a closed convex surface is convex (from which it follows that the immersion is a rigid motion), and that more generally the h-principle cannot hold true for isometric immersions of any elliptic $2$![]() -manifold with or without boundary. Mischa Gromov conjectures in [Reference Gromov26, Section 3.5.5.C, Open Problem 34-36] that the transition threshold is $\alpha =1/2$
-manifold with or without boundary. Mischa Gromov conjectures in [Reference Gromov26, Section 3.5.5.C, Open Problem 34-36] that the transition threshold is $\alpha =1/2$![]() in this case. The best evidence so far for this conjecture is provided in [Reference De Lellis and Inauen15], where the authors show that $C^{1,1/2}$
in this case. The best evidence so far for this conjecture is provided in [Reference De Lellis and Inauen15], where the authors show that $C^{1,1/2}$![]() regularity could be the borderline regularity for the identity of intrinsic covariant derivative of the $2$
regularity could be the borderline regularity for the identity of intrinsic covariant derivative of the $2$![]() -manifold and its geometric interpretation.
-manifold and its geometric interpretation.
This article concerns the fundamental question of the sub-$C^2$![]() regularity scales for which, given an isometric immersion of a flat domain, one is able to make sense of fundamentally geometric objects such as the second fundamental form and the Gauss–Codazzi equations. The final goal is to show that the developability property of such isometric immersions (as defined below in Definition 1.1 and proven for $C^2$
regularity scales for which, given an isometric immersion of a flat domain, one is able to make sense of fundamentally geometric objects such as the second fundamental form and the Gauss–Codazzi equations. The final goal is to show that the developability property of such isometric immersions (as defined below in Definition 1.1 and proven for $C^2$![]() isometries in [Reference Hartman and Nirenberg28]) survives for $C^{1, \alpha }$
isometries in [Reference Hartman and Nirenberg28]) survives for $C^{1, \alpha }$![]() isometric immersions if $\alpha >2/3$
isometric immersions if $\alpha >2/3$![]() . As we shall see, parts of the project, e.g. the definition of the second fundamental form, can be carried over for $\alpha >1/2$
. As we shall see, parts of the project, e.g. the definition of the second fundamental form, can be carried over for $\alpha >1/2$![]() , but our analysis falls short of proving a weak variant of the Codazzi–Mainardi equations for $1/2<\alpha < 2/3$
, but our analysis falls short of proving a weak variant of the Codazzi–Mainardi equations for $1/2<\alpha < 2/3$![]() . In this manner, the question of the optimal threshold remains open in the flat case as it is for the elliptic case.
. In this manner, the question of the optimal threshold remains open in the flat case as it is for the elliptic case.
Before proceeding, it should be mentioned that the developability of flat isometric immersions has been discussed in the literature in other regularity regimes. Pogorelev [Reference Pogorelov52, Theorem 1, p. 603] proves this developability under the rather weak assumptions of $C^1$![]() regularity and the existence and vanishing of the total extrinsic curvature (defined as a measure). This result lies at the background of our conclusion through the analysis made in [Reference Lewicka and Pakzad41] and [Reference Korobkov37, Reference Korobkov38]. On the other hand parallel results have been shown by the second author for $W^{2,2}$
regularity and the existence and vanishing of the total extrinsic curvature (defined as a measure). This result lies at the background of our conclusion through the analysis made in [Reference Lewicka and Pakzad41] and [Reference Korobkov37, Reference Korobkov38]. On the other hand parallel results have been shown by the second author for $W^{2,2}$![]() isometric immersions [Reference Pakzad50], where a slight $C^1$
isometric immersions [Reference Pakzad50], where a slight $C^1$![]() regularity gain in this case is also proven, and by Jerrard in [Reference Jerrard34] for the class of Monge–Ampère functions [Reference Fu24]. The former result was based on observations made by Kirchheim on solutions to the degenerate Monge–Ampère equation [Reference Kirchheim36, Chapter 2], and lead to a subsequent statement regarding the smooth density of isometric immersions. These statements were generalized to higher dimensional domains for the co-dimension 1 case in [Reference Liu and Pakzad43]. The latter approach by Jerrard [Reference Jerrard33, Reference Jerrard34], anchored in geometric measure theory, opened the path for proving $C^1$
regularity gain in this case is also proven, and by Jerrard in [Reference Jerrard34] for the class of Monge–Ampère functions [Reference Fu24]. The former result was based on observations made by Kirchheim on solutions to the degenerate Monge–Ampère equation [Reference Kirchheim36, Chapter 2], and lead to a subsequent statement regarding the smooth density of isometric immersions. These statements were generalized to higher dimensional domains for the co-dimension 1 case in [Reference Liu and Pakzad43]. The latter approach by Jerrard [Reference Jerrard33, Reference Jerrard34], anchored in geometric measure theory, opened the path for proving $C^1$![]() regularity and a full range of developability results for isometric immersions of any dimension and co-dimension of sub-critical Sobolev regularity [Reference Jerrard and Pakzad35].
regularity and a full range of developability results for isometric immersions of any dimension and co-dimension of sub-critical Sobolev regularity [Reference Jerrard and Pakzad35].
1.3. The main result
We first begin by a definition to clarify the notion of developabilty as we understand it.
Definition 1.1 Let $\Omega \subset {\mathbb {R}}^2$![]() be a domain and $u: \Omega \to {\mathbb {R}}^k$
be a domain and $u: \Omega \to {\mathbb {R}}^k$![]() be $C^1$
be $C^1$![]() -smooth. We say $u$
-smooth. We say $u$![]() is developable if for all $x\in \Omega$
is developable if for all $x\in \Omega$![]() , either $u$
, either $u$![]() is affine in a neighbourhood of $x$
is affine in a neighbourhood of $x$![]() , or there exists a line $L_x$
, or there exists a line $L_x$![]() containing $x$
containing $x$![]() such that the Jacobian derivative $\nabla u$
such that the Jacobian derivative $\nabla u$![]() is constant on $l_x$
is constant on $l_x$![]() , the connected component of $x$
, the connected component of $x$![]() in $L_x \cap \Omega$
in $L_x \cap \Omega$![]() .
.
Remark 1.2 For bounded domains, $l_x$![]() is always a segment whose both ends lie on $\partial \Omega$
is always a segment whose both ends lie on $\partial \Omega$![]() . We allow for unbounded domains, and hence $l_x$
. We allow for unbounded domains, and hence $l_x$![]() could be a complete line, a ray or an open segment. With some abuse of notation, we will refer to all of them as ‘segments’ throughout the paper.
could be a complete line, a ray or an open segment. With some abuse of notation, we will refer to all of them as ‘segments’ throughout the paper.
There are other equivalent formulations for the developability whose equivalence we will show further on in propostion 2.1. In particular, local and global developability, as laid out in corollary 2.2, are equivalent. Also, from corollary 2.8 and lemma 2.9 it follows that when $u$![]() is developable, the segments $l_x$
is developable, the segments $l_x$![]() are uniquely determined outside the maximal affine region; they do neither intersect each other nor pass through the local constancy regions of the Jacobian derivative.
are uniquely determined outside the maximal affine region; they do neither intersect each other nor pass through the local constancy regions of the Jacobian derivative.
In this article, we prefer to work with the little Hölder spaces. For our choice of notations and precise definitions of these spaces see § 3. Working with the little Hölder scale pinpoints the needed control—for the effectiveness of our arguments—on the oscillations of the mapping gradient. The corresponding results in the classical Hölder regime is then obtained as a corollary.
The main result of this article is the following theorem:
Theorem 1.3 Let $\Omega \subset {\mathbb {R}}^2$![]() be a domain and $2/3 \le \alpha <1$
be a domain and $2/3 \le \alpha <1$![]() . If $u \in c^ {1,\,\alpha }(\Omega,\, {\mathbb {R}}^3)$
. If $u \in c^ {1,\,\alpha }(\Omega,\, {\mathbb {R}}^3)$![]() is an isometric immersion, then $u$
is an isometric immersion, then $u$![]() is developable. In particular, if $\alpha >2/3,$
is developable. In particular, if $\alpha >2/3,$![]() we have $C^{1,\alpha }(\Omega ) \subset c^{1,2/3} (\Omega )$
we have $C^{1,\alpha }(\Omega ) \subset c^{1,2/3} (\Omega )$![]() and therefore all isometric immersions $u : \Omega \to {\mathbb {R}}^3$
and therefore all isometric immersions $u : \Omega \to {\mathbb {R}}^3$![]() of local $C^ {1,\,\alpha }$
of local $C^ {1,\,\alpha }$![]() regularity are developable.
regularity are developable.
Remark 1.4 Based on the observations made in this article, the proofs of [Reference Conti, De Lellis and Székelyhidi13, Reference Conti, De Lellis and Székelyhidi14] for the rigidity statements are also valid under little Hölder $c^{1,2/3}$![]() regularity assumption. A more difficult task would be to consider other types of regularity regimes, e.g. the fractional Sobolev one. For this direction, see [Reference Li, Pakzad and Schikorra42] and the discussions therein.
regularity assumption. A more difficult task would be to consider other types of regularity regimes, e.g. the fractional Sobolev one. For this direction, see [Reference Li, Pakzad and Schikorra42] and the discussions therein.
Per [Reference Pogorelov52, Theorem 1, p. 603], what we need to show is that the image of the Gauss map $\vec n$![]() is of measure zero. Following [Reference Conti, De Lellis and Székelyhidi13, Corollary 5] it is possible to prove that the Brouwer degree ${\rm deg} (y,\, V ,\,\vec n)$
is of measure zero. Following [Reference Conti, De Lellis and Székelyhidi13, Corollary 5] it is possible to prove that the Brouwer degree ${\rm deg} (y,\, V ,\,\vec n)$![]() of $\vec n$
of $\vec n$![]() of the immersion vanishes for all open sets $V\subset \Omega$
of the immersion vanishes for all open sets $V\subset \Omega$![]() and $y\in {\mathbb {R}}^2$
and $y\in {\mathbb {R}}^2$![]() , when defined. However, this is not sufficient to conclude with the needed statement $|\vec n(\Omega )|=0$
, when defined. However, this is not sufficient to conclude with the needed statement $|\vec n(\Omega )|=0$![]() for developability: Through a similar approach as in [Reference Malý and Martio44, Section 5], for each $\alpha \in (0,\,1)$
for developability: Through a similar approach as in [Reference Malý and Martio44, Section 5], for each $\alpha \in (0,\,1)$![]() , one can construct a map in $C^{0, \alpha }(\Omega,\, {\mathbb {R}}^2)$
, one can construct a map in $C^{0, \alpha }(\Omega,\, {\mathbb {R}}^2)$![]() whose local degree vanishes everywhere, but whose image is onto the unit square. Hence, the zero degree Gauss map could still have an image of positive measure and this obstacle necessitates another strategy. Indeed, our argument uses a slight improvement on the parallel result proved for the degenerate very weak Monge–Ampère equation in [Reference Lewicka and Pakzad41], which uses the degree formula for both the gradient of the solution, and its affine perturbations of positive degree, as follows:
whose local degree vanishes everywhere, but whose image is onto the unit square. Hence, the zero degree Gauss map could still have an image of positive measure and this obstacle necessitates another strategy. Indeed, our argument uses a slight improvement on the parallel result proved for the degenerate very weak Monge–Ampère equation in [Reference Lewicka and Pakzad41], which uses the degree formula for both the gradient of the solution, and its affine perturbations of positive degree, as follows:
The very weak Hessian determinant [Reference Fonseca and Malý21, Reference Iwaniec32] of a given function $v\in W^{1,2}_{loc}(\Omega )$![]() is defined to be
is defined to be

in the sense of distributions. The operator ${\mathcal {D}et}\, D^2$![]() coinsides with the usual Monge–Ampère operator $\det \nabla ^2$
coinsides with the usual Monge–Ampère operator $\det \nabla ^2$![]() when $v\in C^2$
when $v\in C^2$![]() and $\nabla ^2 v$
and $\nabla ^2 v$![]() stands for the Hessian matrix field of $v$
stands for the Hessian matrix field of $v$![]() . (A $C^3$
. (A $C^3$![]() regularity is needed for a straightforward calculation.) The following statement regarding the degenerate Monge–Ampère equation is a crucial ingredient of our analysis (compare with [Reference Lewicka and Pakzad41, Theorem 1.3]).
regularity is needed for a straightforward calculation.) The following statement regarding the degenerate Monge–Ampère equation is a crucial ingredient of our analysis (compare with [Reference Lewicka and Pakzad41, Theorem 1.3]).
Theorem 1.5 Let $\Omega \subset {\mathbb {R}}^2$![]() be an open domain and let $v\in c^{1, 2/3} (\Omega )$
be an open domain and let $v\in c^{1, 2/3} (\Omega )$![]() be such that
be such that
in $\Omega$![]() . Then $v$
. Then $v$![]() is developable.
is developable.
Remark 1.6 Note that per corollary 2.2 the assumption $v\in C^{1,\alpha } (\overline \Omega )$![]() in [Reference Lewicka and Pakzad41, Theorem 1.3] can too be easily relaxed to the local regularity $v\in C^{1,\alpha }(\Omega )$
in [Reference Lewicka and Pakzad41, Theorem 1.3] can too be easily relaxed to the local regularity $v\in C^{1,\alpha }(\Omega )$![]() in any bounded or unbounded domain.
in any bounded or unbounded domain.
Theorem 1.5 can be proved following the exact footsteps of Lewicka and the second author in proving [Reference Lewicka and Pakzad41, Theorem 1.3], taking into account lemma 3.1 and proposition 3.5 below in showing the following degree formulas for any open set $U\subset \Omega$![]() :
:
where $F_\delta (x_1,\, x_2):= \nabla v(x_1,\, x_2 ) + \delta (-x_2,\, x_1)$![]() . See [Reference Lewicka and Pakzad41, Equations (7.6) and (7.9)]. The rest of the proof remains unchanged. We will leave the verification of details to the reader.
. See [Reference Lewicka and Pakzad41, Equations (7.6) and (7.9)]. The rest of the proof remains unchanged. We will leave the verification of details to the reader.
The main strategy of our proof of theorem 1.3 is hence to relate the given isometric immersion $u\in c^{1,2/3}$![]() to a scalar function $v$
to a scalar function $v$![]() which satisfies the assumptions of theorem 1.5: In a first step, we show that a notion of the second fundamental form $A$
which satisfies the assumptions of theorem 1.5: In a first step, we show that a notion of the second fundamental form $A$![]() in the weak sense exists for immersions of $C^{1,\alpha }$
in the weak sense exists for immersions of $C^{1,\alpha }$![]() -regularity for $\alpha >1/2$
-regularity for $\alpha >1/2$![]() . Next, the Codazzi–Mainardi equation is used to prove that if $u$
. Next, the Codazzi–Mainardi equation is used to prove that if $u$![]() is isometric, $A$
is isometric, $A$![]() is curl free, implying that it must be the Hessian matrix of a scalar function, namely the sought after function $v$
is curl free, implying that it must be the Hessian matrix of a scalar function, namely the sought after function $v$![]() . We then show the required regularity for $v$
. We then show the required regularity for $v$![]() , and proceed to prove using the Gauss equation that $v$
, and proceed to prove using the Gauss equation that $v$![]() satisfies the very weak degenerate Monge–Ampère equation as required by the assumptions of theorem 1.5. Finally, we need to prove that developability of $v$
satisfies the very weak degenerate Monge–Ampère equation as required by the assumptions of theorem 1.5. Finally, we need to prove that developability of $v$![]() , as derived from theorem 1.5, implies the developability of the isometric immersion $u$
, as derived from theorem 1.5, implies the developability of the isometric immersion $u$![]() . Apart from theorem 1.5, the $2/3$
. Apart from theorem 1.5, the $2/3$![]() -Hölder exponent regularity is only required for proving that a weak version of Codazzi–Mainardi equations holds for isometric $u \in c^{1,2/3}$
-Hölder exponent regularity is only required for proving that a weak version of Codazzi–Mainardi equations holds for isometric $u \in c^{1,2/3}$![]() , i.e. when we need to show that $A$
, i.e. when we need to show that $A$![]() is curl free.
is curl free.
The article is organized as follows: In § 2, we will present and prove a few statements regarding the developability properties of $C^1$![]() mappings. In § 3, we will gather a few analytical tools which deal with properties of Hölder continuous functions and with quadratic differential expressions in terms of functions of low regularity. In particular, our basic proposition 3.8 will allow us to define a second fundamental form for the immersions of Hölder-type regularity. The subsequent section is dedicated to the definition and properties of this second fundamental form. In § 5, building on the previous sections, we complete the proof of theorem 1.3. Appendix A is dedicated to a side result (proposition A.1) on the developability of each component of the immersion, which can be shown independently with a shorter proof. Finally, in Appendix B the proof of some standard facts regarding little Hölder spaces are presented.
mappings. In § 3, we will gather a few analytical tools which deal with properties of Hölder continuous functions and with quadratic differential expressions in terms of functions of low regularity. In particular, our basic proposition 3.8 will allow us to define a second fundamental form for the immersions of Hölder-type regularity. The subsequent section is dedicated to the definition and properties of this second fundamental form. In § 5, building on the previous sections, we complete the proof of theorem 1.3. Appendix A is dedicated to a side result (proposition A.1) on the developability of each component of the immersion, which can be shown independently with a shorter proof. Finally, in Appendix B the proof of some standard facts regarding little Hölder spaces are presented.
2. Preliminaries: developable mappings
We have gathered in this section a few statements we will need, and their proofs, regarding the developable mappings in two dimensions. Most of the material in this section are well known and can be found in one form or another in the literature on the topic [Reference Chern and Lashof11, Reference Hartman and Nirenberg28–Reference Hornung30, Reference Jerrard34–Reference Korobkov38, Reference Lewicka and Pakzad41, Reference Liu and Pakzad43, Reference Müller and Pakzad46, Reference Pakzad50, Reference Pogorelov52, Reference Venkataramani, Witten, Kramer and Geroch56], but the authors do not know of any instance where the following statements are explicitly formulated in concert. As already observed in [Reference Hornung29], much of the developability properties of a mapping concern the level sets of its Jacobian derivative, so we formulate our statements having the mappings $f= \nabla u$![]() in mind, where $u$
in mind, where $u$![]() is a developable mapping.
is a developable mapping.
2.1. Global vs local developability
Developability can be defined by local or global formulations, which turn out to be equivalent. There is a risk of confusion, which must be avoided, due to slight differences between the possible formulations (see e.g. the footnote on p. 875 in [Reference Korobkov38]). Also, it would be useful to have a set of equivalent statements at hand to streamline the arguments. The following proposition states three equivalent conditions which the Jacobian derivative of a $C^1$![]() mapping can satisfy to be developable:
mapping can satisfy to be developable:
Proposition 2.1 Let $\Omega \subset {\mathbb {R}}^2$![]() be any domain and let $f: \Omega \to {\mathbb {R}}^m$
be any domain and let $f: \Omega \to {\mathbb {R}}^m$![]() . If $f$
. If $f$![]() is continuous, then the following three conditions are equivalent.
is continuous, then the following three conditions are equivalent.
(a) For all $x\in \Omega,$
 either $f$
either $f$ is constant in a neighbourhood of $x$
is constant in a neighbourhood of $x$ , or there exists a line $L$
, or there exists a line $L$ containing $x$
containing $x$ such that $f$
such that $f$ is constant on the connected component of $x$
is constant on the connected component of $x$ in $L\cap \Omega$
in $L\cap \Omega$ .
.(b) For all $x\in \Omega,$
 there exists an open disk $B_x \subset \Omega$
there exists an open disk $B_x \subset \Omega$ centred at $x$
centred at $x$ with the following property: To all $p\in B_x$
with the following property: To all $p\in B_x$ , we can associate a line $L_p$
, we can associate a line $L_p$ containing $p$
containing $p$ such that $f$
such that $f$ is constant on the segment $\tilde l_p =L_p\cap B$
is constant on the segment $\tilde l_p =L_p\cap B$ . Moreover, for any $y,\,z\in B_x$
. Moreover, for any $y,\,z\in B_x$ , ${\tilde l_y \cap \tilde l_z = \emptyset}$
, ${\tilde l_y \cap \tilde l_z = \emptyset}$ , or $\tilde l_y= \tilde l_z$
, or $\tilde l_y= \tilde l_z$ .
.(c) For all $x\in \Omega,$
 there exists an open disk $B_x$
there exists an open disk $B_x$ centred at $x$
centred at $x$ in $\Omega$
in $\Omega$ such that for all $p\in B_x$
such that for all $p\in B_x$ , there exists a line $L \subset {\mathbb {R}}^2$
, there exists a line $L \subset {\mathbb {R}}^2$ containing $p$
containing $p$ so that $f$
so that $f$ is constant on the segment $L\cap B_x$
is constant on the segment $L\cap B_x$ .
.
Corollary 2.2 $u\in C^1(\Omega,\, {\mathbb {R}}^k)$![]() is developable if and only if for any point in $x\in \Omega$
is developable if and only if for any point in $x\in \Omega$![]() , there exists a neighbourhood $V$
, there exists a neighbourhood $V$![]() of $x$
of $x$![]() on which the restriction $u|_{V}$
on which the restriction $u|_{V}$![]() is developable.
is developable.
Remark 2.3 Local regularity assumptions are sufficient in the assumptions of theorems 1.3 and 1.5 because of the equivalence of global and local developability as formulated above.
Remark 2.4 The continuity of $f$![]() is necessary for the implications ${\rm (a)} \Rightarrow {\rm (b),\,\ (c)}$
is necessary for the implications ${\rm (a)} \Rightarrow {\rm (b),\,\ (c)}$![]() in proposition 2.1 as the following example demonstrates. The function
in proposition 2.1 as the following example demonstrates. The function

satisfies condition (a) but not (b) or (c). Also, the geometric configuration of the level sets of $f$![]() in [Reference Pakzad50, Figure 1] shows the necessity of the distinction between the points in the local constancy regions from other points in condition (a). In other words, a global formulation of condition (b) is not a statement equivalent to (b): A continuous function on a convex domain $\Omega$
in [Reference Pakzad50, Figure 1] shows the necessity of the distinction between the points in the local constancy regions from other points in condition (a). In other words, a global formulation of condition (b) is not a statement equivalent to (b): A continuous function on a convex domain $\Omega$![]() can satisfy conditions (a) and (b) while there are points $x\in \Omega$
can satisfy conditions (a) and (b) while there are points $x\in \Omega$![]() such that for no line $L$
such that for no line $L$![]() containing $x$
containing $x$![]() the function is constant on the intersection $L\cap \Omega$
the function is constant on the intersection $L\cap \Omega$![]() .
.
Remark 2.5 In the recent literature on similar problems, global (and hence inequivalent) versions of condition (b) are formulated as ‘developability of $f$![]() ’ in [Reference Kirchheim36, Definition 2.29] and ‘$\Omega$
’ in [Reference Kirchheim36, Definition 2.29] and ‘$\Omega$![]() -developability of $f$
-developability of $f$![]() on $\Omega$
on $\Omega$![]() ’ in [Reference Hornung29, Section 3.1]. On the other hand condition (a) appears in the statement of [Reference Pakzad50, Theorem II], and then in [Reference Müller and Pakzad46] as the ‘condition (L)’. It is also equivalent to $f$
’ in [Reference Hornung29, Section 3.1]. On the other hand condition (a) appears in the statement of [Reference Pakzad50, Theorem II], and then in [Reference Müller and Pakzad46] as the ‘condition (L)’. It is also equivalent to $f$![]() being ‘countably developable’ according to [Reference Hornung29, Definition 1] and [Reference Hornung30]. (Note that [Reference Hornung29, Assumption (24)] is redundant for continuous $f$
being ‘countably developable’ according to [Reference Hornung29, Definition 1] and [Reference Hornung30]. (Note that [Reference Hornung29, Assumption (24)] is redundant for continuous $f$![]() ; see lemma 2.9.) Finally, it is condition (c) that is stated as the property of the gradients (with empty-interior images) of $C^1$
; see lemma 2.9.) Finally, it is condition (c) that is stated as the property of the gradients (with empty-interior images) of $C^1$![]() mappings in the main result of [Reference Korobkov37, Reference Korobkov38]. (This local result was an ingredient of the proof of theorem 1.5 in [Reference Lewicka and Pakzad41].) Generalizations of (a) to weaker regularity or higher dimensional settings can be found in [Reference Jerrard34, Reference Jerrard and Pakzad35, Reference Venkataramani, Witten, Kramer and Geroch56].
mappings in the main result of [Reference Korobkov37, Reference Korobkov38]. (This local result was an ingredient of the proof of theorem 1.5 in [Reference Lewicka and Pakzad41].) Generalizations of (a) to weaker regularity or higher dimensional settings can be found in [Reference Jerrard34, Reference Jerrard and Pakzad35, Reference Venkataramani, Witten, Kramer and Geroch56].
Remark 2.6 The developability of a $C^1$![]() mapping on $\Omega$
mapping on $\Omega$![]() , as formulated in definition 1.1, translates therefore to its Jacobian derivative satisfying condition (a). To clarify some discrepancy in the literature, we emphasize that we prefer to reserve the term developable for those mappings whose Jacobian derivatives are constant along lower dimensional flat strata in one form or another [Reference Jerrard and Pakzad35, Reference Liu and Pakzad43], rather than directly using it for their derivative mappings as done in [Reference Kirchheim36, Definition 2.29] or [Reference Hornung29, Reference Hornung30]. This is for historical reasons, since this term is conventionally used to refer to (ruled) smooth surfaces of zero Gaussian curvature [Reference do Carmo10].
, as formulated in definition 1.1, translates therefore to its Jacobian derivative satisfying condition (a). To clarify some discrepancy in the literature, we emphasize that we prefer to reserve the term developable for those mappings whose Jacobian derivatives are constant along lower dimensional flat strata in one form or another [Reference Jerrard and Pakzad35, Reference Liu and Pakzad43], rather than directly using it for their derivative mappings as done in [Reference Kirchheim36, Definition 2.29] or [Reference Hornung29, Reference Hornung30]. This is for historical reasons, since this term is conventionally used to refer to (ruled) smooth surfaces of zero Gaussian curvature [Reference do Carmo10].
Proof. (a) $\Rightarrow$![]() (b):
(b):
This is implicitly proved in [Reference Liu and Pakzad43, Lemma 3.7]. We pursue a slightly different strategy. For any $f: \Omega \to {\mathbb {R}}$![]() , let $C_{f}$
, let $C_{f}$![]() be the set on which $f$
be the set on which $f$![]() is locally constant:
is locally constant:
Note that $f$![]() is constant on the connected components of the open set $C_{f}$
is constant on the connected components of the open set $C_{f}$![]() . If $f$
. If $f$![]() satisfies condition (a) of the proposition, for each $x\in \Omega \setminus C_f$
satisfies condition (a) of the proposition, for each $x\in \Omega \setminus C_f$![]() we choose a line $L_x$
we choose a line $L_x$![]() so that $f$
so that $f$![]() is constant on the connected component $x$
is constant on the connected component $x$![]() in $L_x\cap \Omega$
in $L_x\cap \Omega$![]() , denoted by $l_x$
, denoted by $l_x$![]() .
.
We begin by the following simple but useful lemma.
Lemma 2.7 Let $f: \Omega \to {\mathbb {R}}^m$![]() be continuous and satisfy condition (a) in proposition 2.1. Let $\Delta \subset \Omega$
be continuous and satisfy condition (a) in proposition 2.1. Let $\Delta \subset \Omega$![]() be a closed triangular domain. If $f$
be a closed triangular domain. If $f$![]() is constant on two edges of $\Delta$
is constant on two edges of $\Delta$![]() , then $f$
, then $f$![]() is constant on $\Delta$
is constant on $\Delta$![]() .
.
Proof. Let $x,\,y,\,z$![]() be the vertices of $\Delta$
be the vertices of $\Delta$![]() and assume that $f$
and assume that $f$![]() is constant on $[x,\,y]$
is constant on $[x,\,y]$![]() and $[x,\,z]$
and $[x,\,z]$![]() . For any point $w\in \Delta \setminus C_f$
. For any point $w\in \Delta \setminus C_f$![]() , $l_w$
, $l_w$![]() must cross one of the two segments $[x,\,y]$
must cross one of the two segments $[x,\,y]$![]() or $[x,\,z]$
or $[x,\,z]$![]() . This implies $f(w) =f(x)$
. This implies $f(w) =f(x)$![]() . If $w\in \Delta \cap C_f$
. If $w\in \Delta \cap C_f$![]() , and if the segment $[w,\,x] \subset C_f$
, and if the segment $[w,\,x] \subset C_f$![]() , then once again $f(w)=f(x)$
, then once again $f(w)=f(x)$![]() . Finally, if $[w,\,x] \not \subset C_f$
. Finally, if $[w,\,x] \not \subset C_f$![]() , let $\tilde w$
, let $\tilde w$![]() be the closest element to $w$
be the closest element to $w$![]() on the segment $[w,\,x]$
on the segment $[w,\,x]$![]() not in $C_{f}$
not in $C_{f}$![]() . We already proved that $f(\tilde w) = f(x)$
. We already proved that $f(\tilde w) = f(x)$![]() . But since $\tilde w$
. But since $\tilde w$![]() is in the closure of the connected component of $w$
is in the closure of the connected component of $w$![]() in $C_{f}$
in $C_{f}$![]() , and $f$
, and $f$![]() is continuous, we have also $f(w) = f(\tilde w) = f(x)$
is continuous, we have also $f(w) = f(\tilde w) = f(x)$![]() . We conclude that $f|_\Delta \equiv f(x)$
. We conclude that $f|_\Delta \equiv f(x)$![]() .
.
We now make a crucial observation on the constancy directions $L_x$![]() .
.
Corollary 2.8 Let $f$![]() be continuous and satisfy condition (a) in proposition 2.1. If $x\in \Omega \setminus C_f$
be continuous and satisfy condition (a) in proposition 2.1. If $x\in \Omega \setminus C_f$![]() , there exists only one line $L$
, there exists only one line $L$![]() for which $f$
for which $f$![]() is constant on the connected component $l$
is constant on the connected component $l$![]() of $x$
of $x$![]() in $L\cap \Omega$
in $L\cap \Omega$![]() .
.
Proof. Let $x\in \Omega \setminus C_f$![]() and assume that for two lines $L \neq \Lambda$
and assume that for two lines $L \neq \Lambda$![]() , $f$
, $f$![]() is constant on the connected components $l$
is constant on the connected components $l$![]() and $\lambda$
and $\lambda$![]() of $x$
of $x$![]() in respectively $L\cap \Omega$
in respectively $L\cap \Omega$![]() and $\Lambda \cap \Omega$
and $\Lambda \cap \Omega$![]() . Choose a disk $B(x,\,\rho ) \subset B(x,\, 2\rho ) \subset \Omega$
. Choose a disk $B(x,\,\rho ) \subset B(x,\, 2\rho ) \subset \Omega$![]() and note that $\partial B(x,\,\rho )$
and note that $\partial B(x,\,\rho )$![]() intersects $l$
intersects $l$![]() and $\lambda$
and $\lambda$![]() on 4 points $x_1,\, x_2 \in l$
on 4 points $x_1,\, x_2 \in l$![]() and $\chi _1,\, \chi _2 \in \lambda$
and $\chi _1,\, \chi _2 \in \lambda$![]() . Now the assumptions of lemma 2.7 is satisfied for the four closed triangular domains with vertices $x,\, x_i,\, \chi _j$
. Now the assumptions of lemma 2.7 is satisfied for the four closed triangular domains with vertices $x,\, x_i,\, \chi _j$![]() , $i,\,j\in \{1,\,2\}$
, $i,\,j\in \{1,\,2\}$![]() . This implies that $x\in C_f$
. This implies that $x\in C_f$![]() , which contradicts the first assumption on $x$
, which contradicts the first assumption on $x$![]() .
.
As a consequence, when $f$![]() is continuous, for each $x\in \Omega \setminus C_f$
is continuous, for each $x\in \Omega \setminus C_f$![]() , there is only one choice for $L_x$
, there is only one choice for $L_x$![]() and there is no ambiguity in the notation. We further observe:
and there is no ambiguity in the notation. We further observe:
Lemma 2.9 Let the continuous mapping $f:\Omega \to {\mathbb {R}}^m$![]() satisfy condition (a) in proposition 2.1. Then for all $x\in \Omega \setminus C_{f}$
satisfy condition (a) in proposition 2.1. Then for all $x\in \Omega \setminus C_{f}$![]() , $l_x \subset \Omega \setminus C_{f}$
, $l_x \subset \Omega \setminus C_{f}$![]() . Moreover, for all $y,\, z\in \Omega \setminus C_{f}$
. Moreover, for all $y,\, z\in \Omega \setminus C_{f}$![]() , $l_y \cap l_z = \emptyset$
, $l_y \cap l_z = \emptyset$![]() , or $l_y = l_z$
, or $l_y = l_z$![]() .
.
Proof. For showing the first conclusion, we argue by contradiction: Let $y \in C_{f} \cap l_x$![]() and let $V$
and let $V$![]() be an open neighbourhood of $y$
be an open neighbourhood of $y$![]() in $\Omega$
in $\Omega$![]() on which $f$
on which $f$![]() is constant. We observe that for $\delta >0$
is constant. We observe that for $\delta >0$![]() small enough $B(x,\,\delta ) \setminus l_x$
small enough $B(x,\,\delta ) \setminus l_x$![]() cannot entirely lie in $C_{f}$
cannot entirely lie in $C_{f}$![]() , since otherwise, $B(x,\,\delta ) \setminus l_x$
, since otherwise, $B(x,\,\delta ) \setminus l_x$![]() having only two connected components on both sides of $l_x$
having only two connected components on both sides of $l_x$![]() , and $f$
, and $f$![]() being continuous, the value of $f$
being continuous, the value of $f$![]() would be constant on $B(x,\,\delta )$
would be constant on $B(x,\,\delta )$![]() , contradicting $x \notin C_{f}$
, contradicting $x \notin C_{f}$![]() . Therefore, there is a sequence $x_k \in \Omega \setminus C_{f}$
. Therefore, there is a sequence $x_k \in \Omega \setminus C_{f}$![]() converging to $x$
converging to $x$![]() such that $f(x_k) \neq f(x)$
such that $f(x_k) \neq f(x)$![]() . Since the value of $f$
. Since the value of $f$![]() on $x_k$
on $x_k$![]() and $x$
and $x$![]() differ, $l_{x_k} \cap l_x =\emptyset$
differ, $l_{x_k} \cap l_x =\emptyset$![]() for all $k$
for all $k$![]() . As $x_k\to x$
. As $x_k\to x$![]() , we deduce that $l_{x_k}$
, we deduce that $l_{x_k}$![]() must locally uniformly converge to $l_x$
must locally uniformly converge to $l_x$![]() . This implies that $l_{x_k} \cap V$
. This implies that $l_{x_k} \cap V$![]() is non-empty for $k$
is non-empty for $k$![]() large enough and hence $f (x_k) = f(y) = f(x)$
large enough and hence $f (x_k) = f(y) = f(x)$![]() , which is a contradiction.
, which is a contradiction.
To prove the second statement, also assume by contradiction that $l_y \neq l_z$![]() and that $x\in l_y \cap l_z \neq \emptyset$
and that $x\in l_y \cap l_z \neq \emptyset$![]() . Choose a disk $B(x,\,\rho ) \subset B(x,\, 2\rho ) \subset \Omega$
. Choose a disk $B(x,\,\rho ) \subset B(x,\, 2\rho ) \subset \Omega$![]() and note that $\partial B(x,\,\rho )$
and note that $\partial B(x,\,\rho )$![]() intersects $l_y$
intersects $l_y$![]() and $l_z$
and $l_z$![]() on four points $y_1,\, y_2 \in l_y$
on four points $y_1,\, y_2 \in l_y$![]() and $z_1,\, z_2 \in l_z$
and $z_1,\, z_2 \in l_z$![]() . Now the assumptions of lemma 2.7 are satisfied for the four closed triangular domains with vertices $x,\, y_i,\, z_j$
. Now the assumptions of lemma 2.7 are satisfied for the four closed triangular domains with vertices $x,\, y_i,\, z_j$![]() , $i,\,j\in \{1,\,2\}$
, $i,\,j\in \{1,\,2\}$![]() . This implies that $x\in C_f$
. This implies that $x\in C_f$![]() , which contradicts the first statement, as $y\notin C_f$
, which contradicts the first statement, as $y\notin C_f$![]() but $x\in l_y \cap C_f$
but $x\in l_y \cap C_f$![]() .
.
We are now ready to prove (b) assuming (a). We first note that condition (b) is obvious if $x\in C_f$![]() . If $x\notin C_f$
. If $x\notin C_f$![]() , without loss of generality, and through rotations, dilations and translations, we can assume that $x= (0,\,0)$
, without loss of generality, and through rotations, dilations and translations, we can assume that $x= (0,\,0)$![]() and that $l_x$
and that $l_x$![]() is parallel to the horizontal axis. We show that we can find $\delta ^-,\, \delta ^+> 0$
is parallel to the horizontal axis. We show that we can find $\delta ^-,\, \delta ^+> 0$![]() such that condition (b) holds true for $B^+(x,\,\delta ^+)$
such that condition (b) holds true for $B^+(x,\,\delta ^+)$![]() and $B^-(x,\, \delta ^-)$
and $B^-(x,\, \delta ^-)$![]() in the upper and lower planes, where the open half disks are defined by
in the upper and lower planes, where the open half disks are defined by
Then we can choose $B= B(x,\, \min \{\delta ^+,\, \delta ^-\})$![]() and the proof is complete.
and the proof is complete.
Without loss of generality we concentrate on the upper half plane. If there exists $\delta ^+ >0$![]() such that $B(x,\,\delta ^+) \subset C_f$
such that $B(x,\,\delta ^+) \subset C_f$![]() , the conclusion is obvious: We choose $L_y$
, the conclusion is obvious: We choose $L_y$![]() always parallel to the horizontal axis. Otherwise there exists a sequence $x_k \notin C_f$
always parallel to the horizontal axis. Otherwise there exists a sequence $x_k \notin C_f$![]() in the upper open half plane converging to $x$
in the upper open half plane converging to $x$![]() . Note that by lemma 2.9, any two (possibly unbounded) segments $l_y,\, l_z$
. Note that by lemma 2.9, any two (possibly unbounded) segments $l_y,\, l_z$![]() do not intersect within $\Omega$
do not intersect within $\Omega$![]() unless they are the same. This implies that $l_{x_k}\cap l_x = \emptyset$
unless they are the same. This implies that $l_{x_k}\cap l_x = \emptyset$![]() and that the $l_{x_k}$
and that the $l_{x_k}$![]() must converge locally uniformly to $l_x$
must converge locally uniformly to $l_x$![]() . We choose $\rho >0$
. We choose $\rho >0$![]() such that the closed rectangular box
such that the closed rectangular box
is a subset of $\Omega$![]() . We let $x^{\pm }_0:= (\pm \rho,\, 0)$
. We let $x^{\pm }_0:= (\pm \rho,\, 0)$![]() , $x^\pm = (\pm \rho,\, \rho )$
, $x^\pm = (\pm \rho,\, \rho )$![]() and choose $k$
and choose $k$![]() large enough such that for $y=x_k$
large enough such that for $y=x_k$![]() , $l_y= l_{x_k}$
, $l_y= l_{x_k}$![]() intersects the two segments $[x_0^\pm,\, x^\pm ]$
intersects the two segments $[x_0^\pm,\, x^\pm ]$![]() in their respective interior points $y^-$
in their respective interior points $y^-$![]() and $y^+$
and $y^+$![]() . The closure of the convex open quadrilateral $P$
. The closure of the convex open quadrilateral $P$![]() created by the four vertices $x^-_0,\, x^+_0,\, y^+,\, y^-$
created by the four vertices $x^-_0,\, x^+_0,\, y^+,\, y^-$![]() lies in $S^+_\rho$
lies in $S^+_\rho$![]() and we have that $[y^-,\, y^+] \subset l_y$
and we have that $[y^-,\, y^+] \subset l_y$![]() and $[x^-_0,\, x^+_0] \subset l_{x}$
and $[x^-_0,\, x^+_0] \subset l_{x}$![]() .
.
We claim that condition (b) is valid for $P$![]() (standing for $B_x$
(standing for $B_x$![]() ), which completes the proof since there exists some $\delta ^+>0$
), which completes the proof since there exists some $\delta ^+>0$![]() , such that $B^+(x,\, \delta ^+)\subset P$
, such that $B^+(x,\, \delta ^+)\subset P$![]() . For any $z\in P$
. For any $z\in P$![]() , if $z\not \in C_f$
, if $z\not \in C_f$![]() , then we can choose $\tilde l_z = l_z \cap P$
, then we can choose $\tilde l_z = l_z \cap P$![]() , which lies between $\tilde l_{x_0}$
, which lies between $\tilde l_{x_0}$![]() and $\tilde l_y$
and $\tilde l_y$![]() . If, on the other hand, $z\in C_f$
. If, on the other hand, $z\in C_f$![]() , let the points $z_1 \in [y^-,\, y^+]$
, let the points $z_1 \in [y^-,\, y^+]$![]() and $z_0 \in [x^-_0,\, x^+_0]$
and $z_0 \in [x^-_0,\, x^+_0]$![]() be those points on $\partial P$
be those points on $\partial P$![]() which lie vertically above and below $z$
which lie vertically above and below $z$![]() . Since $z_0,\, z_1 \notin C_f$
. Since $z_0,\, z_1 \notin C_f$![]() , we can choose the two closest elements of $P\setminus C_f$
, we can choose the two closest elements of $P\setminus C_f$![]() to $z$
to $z$![]() on the segment $[z_0,\, z_1]$
on the segment $[z_0,\, z_1]$![]() , which we name respectively by $\tilde z_0,\, \tilde z_1$
, which we name respectively by $\tilde z_0,\, \tilde z_1$![]() . We observe that $l_{\tilde z_0}$
. We observe that $l_{\tilde z_0}$![]() and $l_{\tilde z_1}$
and $l_{\tilde z_1}$![]() cannot intersect $l_x$
cannot intersect $l_x$![]() and $l_y$
and $l_y$![]() , which contain the upper and lower boundaries of $P$
, which contain the upper and lower boundaries of $P$![]() , and hence will intersect the two vertical boundaries of $P$
, and hence will intersect the two vertical boundaries of $P$![]() between $x^\pm _0$
between $x^\pm _0$![]() and $y^\pm$
and $y^\pm$![]() in $\tilde z^\pm _i$
in $\tilde z^\pm _i$![]() , $i=0,\,1$
, $i=0,\,1$![]() . We claim that $f$
. We claim that $f$![]() is constant in the region $X$
is constant in the region $X$![]() enclosed between $l_{\tilde z_0}$
enclosed between $l_{\tilde z_0}$![]() (which is above $\tilde l_x$
(which is above $\tilde l_x$![]() and below $l_{\tilde z_1}$
and below $l_{\tilde z_1}$![]() ) and $l_{\tilde z_1}$
) and $l_{\tilde z_1}$![]() (which is above $\tilde l_{\tilde z_0}$
(which is above $\tilde l_{\tilde z_0}$![]() and below $\tilde l_y$
and below $\tilde l_y$![]() ) in $P$
) in $P$![]() . Note that $X$
. Note that $X$![]() is the convex quadrilateral created by $\tilde z^-_0,\, \tilde z^+_0,\, \tilde z^+_1,\, \tilde z^-_1$
is the convex quadrilateral created by $\tilde z^-_0,\, \tilde z^+_0,\, \tilde z^+_1,\, \tilde z^-_1$![]() and contains $z$
and contains $z$![]() in its interior.
in its interior.
The latter claim about the constancy of $f$![]() on $X$
on $X$![]() , if proven, completes the proof of the former claim regarding $P$
, if proven, completes the proof of the former claim regarding $P$![]() , since we are free to choose our non-intersecting constancy segments in this region $X$
, since we are free to choose our non-intersecting constancy segments in this region $X$![]() (in particular for $z$
(in particular for $z$![]() ) in a manner that no such two segments intersect within $P$
) in a manner that no such two segments intersect within $P$![]() : If the directions $l_{\tilde z_0}$
: If the directions $l_{\tilde z_0}$![]() and $l_{\tilde z_1}$
and $l_{\tilde z_1}$![]() are parallel, choose the line $L_p$
are parallel, choose the line $L_p$![]() for all points $p\in X$
for all points $p\in X$![]() to be the line parallel to them passing from $p$
to be the line parallel to them passing from $p$![]() . If, on the other hand, the extensions of $l_{\tilde z_0}$
. If, on the other hand, the extensions of $l_{\tilde z_0}$![]() and $l_{\tilde z_1}$
and $l_{\tilde z_1}$![]() meet at a point $q$
meet at a point $q$![]() (outside of $\Omega$
(outside of $\Omega$![]() ), for all $p\in X$
), for all $p\in X$![]() we choose the line $L_p$
we choose the line $L_p$![]() to be the one passing through $p$
to be the one passing through $p$![]() and $q$
and $q$![]() . If $\tilde l_p$
. If $\tilde l_p$![]() , for any $p\in X$
, for any $p\in X$![]() , were to intersect any other $\tilde l_{\tilde p}$
, were to intersect any other $\tilde l_{\tilde p}$![]() for $\tilde p\in P \setminus X$
for $\tilde p\in P \setminus X$![]() , it would have to first intersect one of the two $\tilde l_{\tilde z_i}$
, it would have to first intersect one of the two $\tilde l_{\tilde z_i}$![]() , $i=0,\,1$
, $i=0,\,1$![]() , which does not happen by construction. Note that $X$
, which does not happen by construction. Note that $X$![]() is the connected component of $C_f\cap P$
is the connected component of $C_f\cap P$![]() containing $z$
containing $z$![]() . We can therefore foliate $P$
. We can therefore foliate $P$![]() in constancy segments by exhausting all the connected components of $C_f \cap P$
in constancy segments by exhausting all the connected components of $C_f \cap P$![]() .
.
To prove our final claim, that is the constancy of $f$![]() on the region $X$
on the region $X$![]() , we note that $f$
, we note that $f$![]() is constant on the segment $\tilde l_{\tilde z_1} =[\tilde z^-_1,\, \tilde z^+_1]$
is constant on the segment $\tilde l_{\tilde z_1} =[\tilde z^-_1,\, \tilde z^+_1]$![]() , and on the segment $[\tilde z_0,\, \tilde z_1]$
, and on the segment $[\tilde z_0,\, \tilde z_1]$![]() , whose interior lies in $C_f$
, whose interior lies in $C_f$![]() . Since $\tilde z_1 \in [\tilde z_1^-,\, \tilde z_1^+]$
. Since $\tilde z_1 \in [\tilde z_1^-,\, \tilde z_1^+]$![]() , by lemma 2.7, $f$
, by lemma 2.7, $f$![]() must be constant in the triangular domain created by $\tilde z_0,\, \tilde z^-_1,\, \tilde z_1^+$
must be constant in the triangular domain created by $\tilde z_0,\, \tilde z^-_1,\, \tilde z_1^+$![]() . But then this last assertion implies that $f$
. But then this last assertion implies that $f$![]() is constant on the segments $[\tilde z_0,\, \tilde z^-_1]$
is constant on the segments $[\tilde z_0,\, \tilde z^-_1]$![]() and $[\tilde z_0,\, \tilde z^+_1]$
and $[\tilde z_0,\, \tilde z^+_1]$![]() , which combined with lemma 2.7 again, using the constancy of $f$
, which combined with lemma 2.7 again, using the constancy of $f$![]() on segments $[\tilde z_0,\, \tilde z^-_0]$
on segments $[\tilde z_0,\, \tilde z^-_0]$![]() and $[\tilde z_0,\, \tilde z^+_0] \subset l_{\tilde z_0}$
and $[\tilde z_0,\, \tilde z^+_0] \subset l_{\tilde z_0}$![]() , proves the claim that $f$
, proves the claim that $f$![]() is constant on $X$
is constant on $X$![]() . The proof of (a) $\Rightarrow$
. The proof of (a) $\Rightarrow$![]() (b) is complete.
(b) is complete.
(b) $\Rightarrow$![]() (c):
(c):
It is logically obvious.
(c) $\Rightarrow$![]() (a):
(a):
The proof can be found in the last page of [Reference Lewicka and Pakzad41]. We reproduce it here for completeness. Let $x\in \Omega$![]() and consider a Ball $B_x$
and consider a Ball $B_x$![]() over which condition (c) is satisfied. In particular, $f$
over which condition (c) is satisfied. In particular, $f$![]() is constant on $L_x\cap B_x$
is constant on $L_x\cap B_x$![]() for some line $L_x$
for some line $L_x$![]() passing through $x$
passing through $x$![]() . Now, consider the (possibly infinite) segment
. Now, consider the (possibly infinite) segment
We claim that $c_x$![]() , which contains the segment $L_x\cap B_x$
, which contains the segment $L_x\cap B_x$![]() , is either equal to $l_x$
, is either equal to $l_x$![]() , i.e. the connected component of $x$
, i.e. the connected component of $x$![]() in $L_x\cap \Omega$
in $L_x\cap \Omega$![]() , or $x\in C_f$
, or $x\in C_f$![]() . This proves that $f$
. This proves that $f$![]() is constant either on $l_x$
is constant either on $l_x$![]() , or in a neighbourhood of $x$
, or in a neighbourhood of $x$![]() , and so (a) holds true.
, and so (a) holds true.
We assume that $c_x\neq l_x$![]() , and prove $x\in C_f$
, and prove $x\in C_f$![]() . In this case $c_x$
. In this case $c_x$![]() must admit at least one endpoint within $\Omega$
must admit at least one endpoint within $\Omega$![]() . Let $y \in \Omega$
. Let $y \in \Omega$![]() be that endpoint. Consider the open disk $B_y$
be that endpoint. Consider the open disk $B_y$![]() centred at $y$
centred at $y$![]() in which all points admit constancy segments within $B_y$
in which all points admit constancy segments within $B_y$![]() . Let the line $L_y$
. Let the line $L_y$![]() passing through $y$
passing through $y$![]() be such that $f$
be such that $f$![]() is constant on the segment $L_y \cap B_y$
is constant on the segment $L_y \cap B_y$![]() and let $z,\,w$
and let $z,\,w$![]() be the endpoints of this segment. $L_y$
be the endpoints of this segment. $L_y$![]() and $L_x$
and $L_x$![]() cannot be parallel, since then $c_x$
cannot be parallel, since then $c_x$![]() can be extended along $L_x = L_y$
can be extended along $L_x = L_y$![]() to include either $z$
to include either $z$![]() or $w$
or $w$![]() , which contradicts the fact that it must be a maximal connected constancy subset of $l_x$
, which contradicts the fact that it must be a maximal connected constancy subset of $l_x$![]() . Therefore, we can choose an element $\tilde y \in B_y \cap c_x$
. Therefore, we can choose an element $\tilde y \in B_y \cap c_x$![]() to form an open triangle $\Delta$
to form an open triangle $\Delta$![]() with vertices $\tilde y,\, z,\, w$
with vertices $\tilde y,\, z,\, w$![]() . $f$
. $f$![]() is constant on $[y,\,z]$
is constant on $[y,\,z]$![]() and on $[\tilde y,\, y]$
and on $[\tilde y,\, y]$![]() , where $y\in (z,\,w)$
, where $y\in (z,\,w)$![]() . Since no segment $L_p \cap B_y$
. Since no segment $L_p \cap B_y$![]() departing from a point $p\in \Delta$
departing from a point $p\in \Delta$![]() can reach $\partial B_y$
can reach $\partial B_y$![]() on its both ends without crossing $[w,\,z]$
on its both ends without crossing $[w,\,z]$![]() or $[\tilde y,\, y]$
or $[\tilde y,\, y]$![]() , we deduce that $f |_\Delta \equiv f(y) = f(x)$
, we deduce that $f |_\Delta \equiv f(y) = f(x)$![]() .
.
We observe that $C_f$![]() contains $\Delta$
contains $\Delta$![]() , and hence also the open segment $(\tilde y,\, y)$
, and hence also the open segment $(\tilde y,\, y)$![]() . We have thus found a non-empty interval in $c_x$
. We have thus found a non-empty interval in $c_x$![]() from which we can propagate our local constancy property and so reach to the desired conclusion of $x\in C_f$
from which we can propagate our local constancy property and so reach to the desired conclusion of $x\in C_f$![]() . We argue by contradiction: If $x\notin C_f$
. We argue by contradiction: If $x\notin C_f$![]() , let $\tilde x$
, let $\tilde x$![]() be the closest point to $y$
be the closest point to $y$![]() on $[x,\, y]$
on $[x,\, y]$![]() which is not in $C_f$
which is not in $C_f$![]() . Certainly $C_f \supset (\tilde x ,\, y) \supset (\tilde y ,\,y)$
. Certainly $C_f \supset (\tilde x ,\, y) \supset (\tilde y ,\,y)$![]() and $(x,\,y) \supset (\tilde x,\, y)$
and $(x,\,y) \supset (\tilde x,\, y)$![]() . Consider once more the open disk $B_{\tilde x}$
. Consider once more the open disk $B_{\tilde x}$![]() according to condition (c). Since $C_f$
according to condition (c). Since $C_f$![]() is open, for some $\hat y\in (\tilde x,\, y)$
is open, for some $\hat y\in (\tilde x,\, y)$![]() close enough to $\tilde x$
close enough to $\tilde x$![]() , $f$
, $f$![]() is constant on a segment $[\hat z,\, \hat w]\subset B_{\tilde x} \cap C_f$
is constant on a segment $[\hat z,\, \hat w]\subset B_{\tilde x} \cap C_f$![]() orthogonal to $c_x$
orthogonal to $c_x$![]() at $\hat y$
at $\hat y$![]() , with $\hat y \in (\hat z ,\, \hat w)$
, with $\hat y \in (\hat z ,\, \hat w)$![]() . Also note that for $\hat x \in [x,\, \hat y)$
. Also note that for $\hat x \in [x,\, \hat y)$![]() , $f$
, $f$![]() is constant on the portion $[\hat x,\, \hat y] = [x,\, \hat y] \cap B_{\tilde x} \supset [\tilde x,\, \hat y]$
is constant on the portion $[\hat x,\, \hat y] = [x,\, \hat y] \cap B_{\tilde x} \supset [\tilde x,\, \hat y]$![]() of the segment $[x,\, \hat y] \subset c_x$
of the segment $[x,\, \hat y] \subset c_x$![]() . Since $f$
. Since $f$![]() takes the value $f(x)$
takes the value $f(x)$![]() on both of $[\hat x,\, \hat y]$
on both of $[\hat x,\, \hat y]$![]() and $[\hat z,\, \hat w]$
and $[\hat z,\, \hat w]$![]() , both within the set $B_{\tilde x}$
, both within the set $B_{\tilde x}$![]() , a similar argument as above shows that $f$
, a similar argument as above shows that $f$![]() is constant on the open triangle $\hat \Delta$
is constant on the open triangle $\hat \Delta$![]() with vertices $\hat x,\, \hat z,\, \hat w$
with vertices $\hat x,\, \hat z,\, \hat w$![]() , and so $\hat \Delta \subset C_f$
, and so $\hat \Delta \subset C_f$![]() . But then $\tilde x \in (\hat x,\, \hat y) \subset \hat \Delta \subset C_f$
. But then $\tilde x \in (\hat x,\, \hat y) \subset \hat \Delta \subset C_f$![]() , which contradicts its choice.
, which contradicts its choice.
In view of proposition 2.1, and as already observed in [Reference Kirchheim36, Proposition 2.30], we have:
Corollary 2.10 Let $\Omega \subset {\mathbb {R}}^2$![]() be a domain and let the continuous mapping $f: \Omega \to {\mathbb {R}}^m$
be a domain and let the continuous mapping $f: \Omega \to {\mathbb {R}}^m$![]() satisfy any of the equivalent conditions in proposition 2.1. Then for all $x\in \Omega$
satisfy any of the equivalent conditions in proposition 2.1. Then for all $x\in \Omega$![]() , there exists $L>0$
, there exists $L>0$![]() , an open disk $B$
, an open disk $B$![]() centred at $x$
centred at $x$![]() , and a unit Lipschitz vector field $\vec \eta : B \to {\mathbb {R}}^2$
, and a unit Lipschitz vector field $\vec \eta : B \to {\mathbb {R}}^2$![]() with ${\rm Lip}\, \vec \eta \le L$
with ${\rm Lip}\, \vec \eta \le L$![]() , for which
, for which
Proof. We choose a disk $B_x = B(x,\, 2\delta ) \subset \Omega$![]() according to condition (b) and we let $B=B(x,\, \delta )$
according to condition (b) and we let $B=B(x,\, \delta )$![]() . For any $p\in B$
. For any $p\in B$![]() , there exists a line $L_p$
, there exists a line $L_p$![]() such that $f$
such that $f$![]() is constant on $\tilde l_p = L_p \cap B_x$
is constant on $\tilde l_p = L_p \cap B_x$![]() , and no two such lines meet within $B_x$
, and no two such lines meet within $B_x$![]() . We define the mapping ${\bf \Lambda }: B\to {\mathbb {R}}\mathbb {P}^1$
. We define the mapping ${\bf \Lambda }: B\to {\mathbb {R}}\mathbb {P}^1$![]() which associates to each point $p\in B$
which associates to each point $p\in B$![]() the element of the real projective line ${\mathbb {R}}\mathbb {P}^1$
the element of the real projective line ${\mathbb {R}}\mathbb {P}^1$![]() determined by the direction of $L_p$
determined by the direction of $L_p$![]() , and we note that it is constant along the segments $L_p\cap B$
, and we note that it is constant along the segments $L_p\cap B$![]() and continuous. Since $B$
and continuous. Since $B$![]() is simply connected, ${\bf \Lambda }$
is simply connected, ${\bf \Lambda }$![]() can be lifted to a continuous mapping $\vec \eta : B \to \mathbb {S}^1$
can be lifted to a continuous mapping $\vec \eta : B \to \mathbb {S}^1$![]() . By constancy of ${\bf \Lambda }$
. By constancy of ${\bf \Lambda }$![]() along the segments $L_p\cap B$
along the segments $L_p\cap B$![]() , $\vec \eta$
, $\vec \eta$![]() can only take two distinct values along them, and so its continuity implies that $\vec \eta$
can only take two distinct values along them, and so its continuity implies that $\vec \eta$![]() is constant along these directions, which are now determined by $\vec \eta$
is constant along these directions, which are now determined by $\vec \eta$![]() itself. Since two distinct lines $L_p$
itself. Since two distinct lines $L_p$![]() and $L_q$
and $L_q$![]() , for $p,\,q\in B$
, for $p,\,q\in B$![]() , do not meet except possibly at an at least a $\delta$
, do not meet except possibly at an at least a $\delta$![]() -distance from $\partial B$
-distance from $\partial B$![]() , we conclude that ${\rm Lip} \,\vec \eta \le 1/\delta$
, we conclude that ${\rm Lip} \,\vec \eta \le 1/\delta$![]() .
.
2.2. Developability through test functions
The following lemma will allow us to translate the developability properties of $v\in C^{1}$![]() into a property for the distribution $\nabla ^2 v$
into a property for the distribution $\nabla ^2 v$![]() :
:
Lemma 2.11 Let $B\subset {\mathbb {R}}^2$![]() be an open disk and $f :B \to {\mathbb {R}}^m$
be an open disk and $f :B \to {\mathbb {R}}^m$![]() be continuous. Also, let $\vec \eta : B\to {\mathbb {R}}^2$
be continuous. Also, let $\vec \eta : B\to {\mathbb {R}}^2$![]() be a unit Lipschitz vector field such that the following property holds true:
be a unit Lipschitz vector field such that the following property holds true:
Then the following two properties are equivalent:
(a) $\displaystyle \displaystyle \forall x\in B \quad f (x) = f (x+ s \vec \eta (x)) \,\, \mbox {for all} \, s \, \mbox {for which} \,\, x+ s \vec \eta (x) \in B$
 ,
,(b) $\displaystyle \forall \psi \in C^\infty _c(B) \quad \int _B f {\rm div} (\psi \vec \eta ) =0.$

Proof. condition (b) states that the distributional derivative of $f$![]() in direction of the vector field $\vec \eta$
in direction of the vector field $\vec \eta$![]() vanishes. The proof shows that a regular enough change of variable reduces the problem to the case when $\vec \eta$
vanishes. The proof shows that a regular enough change of variable reduces the problem to the case when $\vec \eta$![]() is constant.
is constant.
Let $\vec \xi = \vec \eta ^\perp$![]() and $x \in B$
and $x \in B$![]() . Choose $T_0>0$
. Choose $T_0>0$![]() such that $\gamma : (-T_0,\,T_0) \to B$
such that $\gamma : (-T_0,\,T_0) \to B$![]() is a solution to the ODE $\gamma ' (t) = \vec \xi (\gamma (t))$
is a solution to the ODE $\gamma ' (t) = \vec \xi (\gamma (t))$![]() in $B$
in $B$![]() with initial value $\gamma (0) =x$
with initial value $\gamma (0) =x$![]() . Let $L = {\rm Lip} \,\vec \eta$
. Let $L = {\rm Lip} \,\vec \eta$![]() , $k(t)= -\gamma ''(t) \cdot \vec \eta (\gamma (t))$
, $k(t)= -\gamma ''(t) \cdot \vec \eta (\gamma (t))$![]() and note that $\|k\|_{L^\infty (-T_0, T_0)} \le L$
and note that $\|k\|_{L^\infty (-T_0, T_0)} \le L$![]() . It is straightforward to see that there exists $0< t_0\le T_0/2$
. It is straightforward to see that there exists $0< t_0\le T_0/2$![]() such that for all $t,\, t'\in [-t_0,\,t_0]$
such that for all $t,\, t'\in [-t_0,\,t_0]$![]() , and all $s,\, s' \in {\mathbb {R}}$
, and all $s,\, s' \in {\mathbb {R}}$![]() ,
,
unless $t=t'$![]() and $s=s'$
and $s=s'$![]() . Indeed, assume by contradiction that there exist sequences $t_k,\, t'_k\to 0$
. Indeed, assume by contradiction that there exist sequences $t_k,\, t'_k\to 0$![]() , $s_k,\, s'_k$
, $s_k,\, s'_k$![]() , such that for all $k$
, such that for all $k$![]() , $(t_k,\, s_k) \neq (t'_k,\, s'_k)$
, $(t_k,\, s_k) \neq (t'_k,\, s'_k)$![]() , and
, and
Note that $t_k = t'_k$![]() implies $s_k = s'_k$
implies $s_k = s'_k$![]() , and hence we must have $t_k \neq t'_k$
, and hence we must have $t_k \neq t'_k$![]() for all $k$
for all $k$![]() , implying on its turn that $\gamma (t_k) \neq \gamma (t'_k)$
, implying on its turn that $\gamma (t_k) \neq \gamma (t'_k)$![]() for all $k$
for all $k$![]() . On the other hand, by the main property of $\vec \eta$
. On the other hand, by the main property of $\vec \eta$![]() we obtain
we obtain
This yields
implying that
Passing to the limit we obtain $|\vec \xi (x)|^2 = \gamma '(0) \cdot \vec \xi (\gamma (0)) =0$![]() , which is a contradiction.
, which is a contradiction.
Since $\gamma ([-t_0,\, t_0])$![]() is compact in $B$
is compact in $B$![]() , we choose $0< s_0< 1/{2L}$
, we choose $0< s_0< 1/{2L}$![]() such that the image of $[-t_0,\, t_0] \times [-s_0,\, s_0]$
such that the image of $[-t_0,\, t_0] \times [-s_0,\, s_0]$![]() under
under
lies compactly in $B$![]() . We note that $\Phi$
. We note that $\Phi$![]() is one-to-one and Lipschitz on $U:= (-t_0,\,t_0) \times (-s_0,\, s_0)$
is one-to-one and Lipschitz on $U:= (-t_0,\,t_0) \times (-s_0,\, s_0)$![]() and that we have
and that we have
We conclude that $\Phi :U \to \Phi (U)$![]() is a bilipschitz change of variable.
is a bilipschitz change of variable.
We let $V_x= \Phi (U)$![]() , which is an open neighbourhood of $x$
, which is an open neighbourhood of $x$![]() in $B$
in $B$![]() . We calculate for any $\psi \in C^\infty _c(V_x)$
. We calculate for any $\psi \in C^\infty _c(V_x)$![]() :
:
which gives for $\tilde \psi = \psi \circ \Phi$![]() :
:
Therefore, letting $\tilde f (t,\,s) = f \circ \Phi (s,\,t)= f(\gamma (t) + s \vec \eta (\gamma (t))$![]() we obtain
we obtain

If (a) is satisfied, then $\tilde f(t,\,s) = \tilde f(t)$![]() for all values of $s$
for all values of $s$![]() for which the function is defined, and hence, since $\tilde \psi$
for which the function is defined, and hence, since $\tilde \psi$![]() is compactly supported in $U$
is compactly supported in $U$![]() , we obtain:
, we obtain:
Now for $\psi \in C^\infty _c(B)$![]() , we let $K:= {\rm supp}(\psi ) \subset B$
, we let $K:= {\rm supp}(\psi ) \subset B$![]() . $K$
. $K$![]() is compact and so it admits a finite covering of open sets of the form $V_{x_i}$
is compact and so it admits a finite covering of open sets of the form $V_{x_i}$![]() , for $i=1,\, \cdots,\, n$
, for $i=1,\, \cdots,\, n$![]() . We consider a partition of unity associated with this covering
. We consider a partition of unity associated with this covering

and we conclude with (b) by (2.2):

To prove the converse, assume (b) and let $\varphi \in L^1 (U)$![]() , be such that
, be such that
and define

We can construct a sequence $\psi _k \in C^{0,1}_c(V_x)$![]() such that
such that
Therefore by (b)
which in view of (2.1) implies

This fact being true for all $\varphi \in L^1(U)$![]() satisfying (2.3) implies that
satisfying (2.3) implies that
This means that for $|s|< s_0$![]() :
:
Global property (a) is a direct consequence of this local property around each $x\in B$![]() , and the fact that $\vec \eta$
, and the fact that $\vec \eta$![]() itself is constant on $x+ s\vec \eta (x)\in B$
itself is constant on $x+ s\vec \eta (x)\in B$![]() for all $s$
for all $s$![]() .
.
3. A Hölder continuity toolbox
3.1. Notations
For any open set $U \subset {\mathbb {R}}^n$![]() , sufficiently differentiable function $f:U \to {\mathbb {R}}$
, sufficiently differentiable function $f:U \to {\mathbb {R}}$![]() , and nonnegative integer $j$
, and nonnegative integer $j$![]() we will denote by $[\cdot ]_{j;U}$
we will denote by $[\cdot ]_{j;U}$![]() the supremum norm of its $j$
the supremum norm of its $j$![]() th (multi-index) derivatives over $U$
th (multi-index) derivatives over $U$![]() and by
and by

its $C^k$![]() norm. For $0<\alpha \le 1$
norm. For $0<\alpha \le 1$![]() , the corresponding Hölder seminorms and norms are identified by the standard conventions
, the corresponding Hölder seminorms and norms are identified by the standard conventions

The modulus of continuity of $f: U \to {\mathbb {R}}$![]() is defined by
is defined by

We also introduce the $\alpha$![]() -Hölder modulus of $f$
-Hölder modulus of $f$![]() for $0<\alpha <1$
for $0<\alpha <1$![]() :
:

We will drop the subscript $U$![]() when denoting these quantities for the specific case of an open set named $U$
when denoting these quantities for the specific case of an open set named $U$![]() , hence $\|\cdot \|_{\cdot }= \|\cdot \|_{\cdot ;U}$
, hence $\|\cdot \|_{\cdot }= \|\cdot \|_{\cdot ;U}$![]() , etc.
, etc.
For a fixed mollifying kernel $\phi \in C^\infty _c(B(0,\,1))$![]() with $\int \phi =1$
with $\int \phi =1$![]() , and $x\in {\mathbb {R}}^n$
, and $x\in {\mathbb {R}}^n$![]() , we denote the standard convolution of a given mapping $f$
, we denote the standard convolution of a given mapping $f$![]() with $\phi$
with $\phi$![]() over the length scale $\varepsilon$
over the length scale $\varepsilon$![]() by
by
where for all $x$![]()
Naturally $f_\varepsilon (x)$![]() is defined for $\varepsilon$
is defined for $\varepsilon$![]() small enough provided $f$
small enough provided $f$![]() is integrable in some neighbourhood of $x$
is integrable in some neighbourhood of $x$![]() .
.
Throughout this article, the universally bounded constant $c=O(1)$![]() might change but is independent of all the data, unless specified by an argument. We will also use the usual little-$o$
might change but is independent of all the data, unless specified by an argument. We will also use the usual little-$o$![]() convention, i.e. for any two functions $b,\, \tilde b : [0,\, \varepsilon _0) \to {\mathbb {R}}^+$
convention, i.e. for any two functions $b,\, \tilde b : [0,\, \varepsilon _0) \to {\mathbb {R}}^+$![]() , we have:
, we have:
We will repeatedly refer to the following convolution estimates in our arguments:
Lemma 3.1 Let $V\subset U\subset {\mathbb {R}}^n$![]() be open sets such that ${\rm dist}{(\overline V,\, \partial U)} >0$
be open sets such that ${\rm dist}{(\overline V,\, \partial U)} >0$![]() . Assume that $f,\,h: U\to {\mathbb {R}}$
. Assume that $f,\,h: U\to {\mathbb {R}}$![]() are locally integrable. Then for any $0<\alpha <1$
are locally integrable. Then for any $0<\alpha <1$![]() and $\varepsilon < {\rm dist} (\overline V,\, \partial U)$
and $\varepsilon < {\rm dist} (\overline V,\, \partial U)$![]() :
:
(i) $\|f_\varepsilon - f\|_{0;V} \le c[f]_{0,\alpha |\varepsilon } \varepsilon ^\alpha$
 ,
,(ii) $\|\nabla f_\varepsilon \|_{0;V} \le c[f]_{0,\alpha |\varepsilon } \varepsilon ^{\alpha -1}$
 ,
,(iii) $\|f_\varepsilon h_\varepsilon - (fh)_\varepsilon \|_{1;V} \le c[f]_{0,\alpha |\varepsilon } [h]_{0,\alpha |\varepsilon }\varepsilon ^{2\alpha -1}$
 .
.
Note the basic estimate
Based on this estimate, the proof follows the same lines as in [Reference Conti, De Lellis and Székelyhidi13, Lemma 1] and is left to the reader. The commutator estimate lemma 3.1-(iii) will be crucial for our analysis. It will be used to prove the quadratic estimate (4.5) ([Reference Conti, De Lellis and Székelyhidi13, Proposition 1]) for the pull-back metric of mollified isometric immersions. It is also a necessary ingredient of the proof of theorem 1.5 through establishing the degree formulas (1.1) for $v\in c^{1,2/3}$![]() , following [Reference Lewicka and Pakzad41].
, following [Reference Lewicka and Pakzad41].
3.2. Little Hölder spaces
Our goal here is to define and characterize the elements of the little Hölder spaces $c^{1,\alpha }$![]() . We denote by $C^k(U)$
. We denote by $C^k(U)$![]() the functions which are continuously differentiable up to the $k$
the functions which are continuously differentiable up to the $k$![]() th order in $U$
th order in $U$![]() , and by $C^k(\overline U)$
, and by $C^k(\overline U)$![]() the functions whose derivatives up to order $k$
the functions whose derivatives up to order $k$![]() in $U$
in $U$![]() exist and admit a continuous extension to $\overline U$
exist and admit a continuous extension to $\overline U$![]() . For any open bounded weakly Lipschitz domain $U\subset {\mathbb {R}}^n$
. For any open bounded weakly Lipschitz domain $U\subset {\mathbb {R}}^n$![]() , we recall the definition of the Hölder space
, we recall the definition of the Hölder space
By uniform continuity of derivatives, all the derivatives of $f$![]() up to the order $k$
up to the order $k$![]() have continuous extensions to $\overline U$
have continuous extensions to $\overline U$![]() and so $C^{k, \alpha } (\overline U) \subset C^k(\overline U)$
and so $C^{k, \alpha } (\overline U) \subset C^k(\overline U)$![]() . For an arbitrary open set $\Omega \subset {\mathbb {R}}^n$
. For an arbitrary open set $\Omega \subset {\mathbb {R}}^n$![]() we say $f\in C^{k,\alpha }(\Omega )$
we say $f\in C^{k,\alpha }(\Omega )$![]() if and only if for any point $x\in \Omega$
if and only if for any point $x\in \Omega$![]() , $f\in C^{k,\alpha }(\overline U)$
, $f\in C^{k,\alpha }(\overline U)$![]() for some open neighbourhood $U\subset \Omega$
for some open neighbourhood $U\subset \Omega$![]() of $x$
of $x$![]() .
.
Remark 3.2 We have restricted our attention to weakly Lipschitz bounded domains $U$![]() in order to insure the inclusion $C^1(\overline U) \subset C^{0,\alpha }(\overline U)$
in order to insure the inclusion $C^1(\overline U) \subset C^{0,\alpha }(\overline U)$![]() and to avoid unnecessary technical complications in what follows.
and to avoid unnecessary technical complications in what follows.
Definition 3.3 Let $0<\alpha < 1$![]() and $U\subset {\mathbb {R}}^n$
and $U\subset {\mathbb {R}}^n$![]() be an open bounded weakly Lipschitz domain. The little Hölder space $c^{0,\alpha }(\overline U)$
be an open bounded weakly Lipschitz domain. The little Hölder space $c^{0,\alpha }(\overline U)$![]() is the closure of $C^1(\overline U)$
is the closure of $C^1(\overline U)$![]() with respect to $\|\cdot \|_{0,\alpha ;U}$
with respect to $\|\cdot \|_{0,\alpha ;U}$![]() in $C^{0,\alpha }(\overline U)$
in $C^{0,\alpha }(\overline U)$![]() . For any open set $\Omega \subset {\mathbb {R}}^n$
. For any open set $\Omega \subset {\mathbb {R}}^n$![]() , we say $f\in c^{0,\alpha }(\Omega )$
, we say $f\in c^{0,\alpha }(\Omega )$![]() if and only if for any point $x\in \Omega$
if and only if for any point $x\in \Omega$![]() , $f\in c^{0,\alpha }(\overline U)$
, $f\in c^{0,\alpha }(\overline U)$![]() for an open neighbourhood $U\subset \Omega$
for an open neighbourhood $U\subset \Omega$![]() of $x$
of $x$![]() . For $k\in \mathbb {N}$
. For $k\in \mathbb {N}$![]() , the space $c^{k,\alpha }(\overline U)$
, the space $c^{k,\alpha }(\overline U)$![]() (resp. $c^{k,\alpha } (\Omega )$
(resp. $c^{k,\alpha } (\Omega )$![]() ) is defined to be the set of all functions $f \in C^k(U)$
) is defined to be the set of all functions $f \in C^k(U)$![]() (resp. $C^k(\Omega )$
(resp. $C^k(\Omega )$![]() ) for which the components of $D^k f$
) for which the components of $D^k f$![]() belong to $c^{0,\alpha }(\overline U)$
belong to $c^{0,\alpha }(\overline U)$![]() (resp. $c^{0,\alpha }(\Omega )$
(resp. $c^{0,\alpha }(\Omega )$![]() ).
).
Remark 3.4 Under the above regularity assumptions on $U$![]() , it can be shown that $c^{k,\alpha }(\overline U)$
, it can be shown that $c^{k,\alpha }(\overline U)$![]() is the closure of $C^\infty (\overline U)$
is the closure of $C^\infty (\overline U)$![]() in $C^{k,\alpha }(\overline U)$
in $C^{k,\alpha }(\overline U)$![]() . We will not use this fact in our arguments.
. We will not use this fact in our arguments.
It is useful to identify the elements of the little Hölder spaces in terms of their modulus of continuity. In this regard we state the following well-known equivalence, whose proof is presented for the sake of completeness (see also Appendix B).
Proposition 3.5 Let $U$![]() be a bounded weakly Lipschitz domain, $0<\alpha < 1$
be a bounded weakly Lipschitz domain, $0<\alpha < 1$![]() . Then the following statements are equivalent.
. Then the following statements are equivalent.
(i) $f\in c^{0, \alpha }(\overline U)$
 .
.(ii) $f: U\to {\mathbb {R}}$
 admits an extension $\tilde f\in c^{0,\alpha } ({\mathbb {R}}^n)$
admits an extension $\tilde f\in c^{0,\alpha } ({\mathbb {R}}^n)$ and $\tilde f_\varepsilon |_U \to f$
and $\tilde f_\varepsilon |_U \to f$ in $C^{0,\alpha }(\overline U)$
in $C^{0,\alpha }(\overline U)$ .
.(iii) $\omega _{f;U}(r)$
 is $o(r^\alpha )$
is $o(r^\alpha )$ .
.(iv) $\displaystyle \lim _{r\to 0} [f]_{0,\alpha ;U|r} =0$
 .
.
Proof. (i) $\Rightarrow$![]() (iv): Assuming $f\in c^{0,\alpha }(\overline U)$
(iv): Assuming $f\in c^{0,\alpha }(\overline U)$![]() , let $f_k\in C^1 (\overline U)$
, let $f_k\in C^1 (\overline U)$![]() be a sequence of functions converging to $f$
be a sequence of functions converging to $f$![]() in $C^{0,\alpha }(\overline U)$
in $C^{0,\alpha }(\overline U)$![]() as $k\to \infty$
as $k\to \infty$![]() . We estimate:
. We estimate:
and a straightforward argument by the auxiliary argument $k$![]() implies the required convergence.
implies the required convergence.
(iv) $\Rightarrow$![]() (iii): This is straightforward since for all $r>0$
(iii): This is straightforward since for all $r>0$![]() :
:
(iii) $\Rightarrow$![]() (ii): By the assumption $f$
(ii): By the assumption $f$![]() is uniformly continuous in $U$
is uniformly continuous in $U$![]() . We extend $f$
. We extend $f$![]() to $\tilde f: {\mathbb {R}}^n\to {\mathbb {R}}$
to $\tilde f: {\mathbb {R}}^n\to {\mathbb {R}}$![]() by applying proposition B.2, obtaining that $\omega _{\tilde f;{\mathbb {R}}^n}(r) \le C \omega _{f;U} (r)$
by applying proposition B.2, obtaining that $\omega _{\tilde f;{\mathbb {R}}^n}(r) \le C \omega _{f;U} (r)$![]() is $o(r^\alpha )$
is $o(r^\alpha )$![]() . We conclude that
. We conclude that
is $o(1)$![]() as a function of $r$
as a function of $r$![]() . Consider any bounded weakly Lipschitz domain $V\subset {\mathbb {R}}^n$
. Consider any bounded weakly Lipschitz domain $V\subset {\mathbb {R}}^n$![]() and note that $\tilde f|_V \in C^{0,\alpha }(\overline V)$
and note that $\tilde f|_V \in C^{0,\alpha }(\overline V)$![]() . Applying lemma B.1 to $V$
. Applying lemma B.1 to $V$![]() implies that $\tilde f_\varepsilon |_V \to \tilde f|_V$
implies that $\tilde f_\varepsilon |_V \to \tilde f|_V$![]() in $C^{0,\alpha }(\overline V)$
in $C^{0,\alpha }(\overline V)$![]() as $\varepsilon \to 0$
as $\varepsilon \to 0$![]() and thus $\tilde f|_V \in c^{0,\alpha } (\overline V)$
and thus $\tilde f|_V \in c^{0,\alpha } (\overline V)$![]() . Both conclusions in (ii) follow.
. Both conclusions in (ii) follow.
(ii) $\Rightarrow$![]() (i): This statement trivially follows from definition 3.3.
(i): This statement trivially follows from definition 3.3.
Corollary 3.6 Let $0<\alpha <\beta <1$![]() and let $U\subset {\mathbb {R}}^n$
and let $U\subset {\mathbb {R}}^n$![]() be a bounded weakly Lipschitz domain. Then $c^{1,\beta }(\overline U) \subsetneq C^{1,\beta } (\overline U) \subsetneq c^{1,\alpha }(\overline U)$
be a bounded weakly Lipschitz domain. Then $c^{1,\beta }(\overline U) \subsetneq C^{1,\beta } (\overline U) \subsetneq c^{1,\alpha }(\overline U)$![]() .
.
Proof. The first inclusion is trivial. If $f\in C^{1,\beta } (\overline U)$![]() , then $\omega _{f;U}(r)$
, then $\omega _{f;U}(r)$![]() is $O(r^\beta )$
is $O(r^\beta )$![]() and so the second inclusion follows by proposition 3.5.
and so the second inclusion follows by proposition 3.5.
3.3. A distributional product and a criteria for Hölder continuity
The following two propositions are practically known by the community at large. Similar or more general statements in the same spirit have appeared in various contexts, e.g. in the discussion of the Young integral [Reference Young58] or of the paraproducts [Reference Runst and Sickel53, Chapter 4]. For example, see [Reference Bahouri, Chemin and Danchin2, Theorem 2.52] and [Reference Friz and Hairer23, Theorem 13.16], or compare with [Reference Marschall45, Theorem 22]. Here, we have formulated and proved rather accessible straightforward versions for the little Hölder spaces which are more adapted to our needs.
Definition 3.7 Let $U\subset {\mathbb {R}}^n$![]() be a bounded weakly Lipschitz domain. We say that a distribution $T\in \mathcal {D}'(U,\,{\mathbb {R}}^n)$
be a bounded weakly Lipschitz domain. We say that a distribution $T\in \mathcal {D}'(U,\,{\mathbb {R}}^n)$![]() satisfies the $\alpha$
satisfies the $\alpha$![]() -interpolation property on $W^{1,1}_0(U)$
-interpolation property on $W^{1,1}_0(U)$![]() whenever for $C>0$
whenever for $C>0$![]()
We say that $T$![]() satisfies the fine $\alpha$
satisfies the fine $\alpha$![]() -interpolation property on $W^{1,1}_0(U)$
-interpolation property on $W^{1,1}_0(U)$![]() whenever for $C>0$
whenever for $C>0$![]()
with $\delta (1)= +\infty$![]()
Proposition 3.8 Let $U\subset {\mathbb {R}}^n$![]() be a bounded weakly Lipschitz domain and $V \Subset U$
be a bounded weakly Lipschitz domain and $V \Subset U$![]() be an open set compactly contained in $U$
be an open set compactly contained in $U$![]() . Let $0 < \alpha < 1$
. Let $0 < \alpha < 1$![]() , $f \in C^{0,\alpha } (\overline U)$
, $f \in C^{0,\alpha } (\overline U)$![]() and $h\in c^{0,\alpha }(\overline U)$
and $h\in c^{0,\alpha }(\overline U)$![]() . If $\alpha >1/2$
. If $\alpha >1/2$![]() , then as $\varepsilon \to 0$
, then as $\varepsilon \to 0$![]() , for all $j=1,\,\cdots n$
, for all $j=1,\,\cdots n$![]() the sequence $f_\varepsilon \partial _j h_\varepsilon$
the sequence $f_\varepsilon \partial _j h_\varepsilon$![]() converges in the sense of distributions to a distribution on $V$
converges in the sense of distributions to a distribution on $V$![]() which we denote by $f\partial _j h$
which we denote by $f\partial _j h$![]() . More precisely, the convergence is in the dual of $W^{1,1}_0(V)$
. More precisely, the convergence is in the dual of $W^{1,1}_0(V)$![]() , i.e. if $\psi \in W^{1,1}_0(V)$
, i.e. if $\psi \in W^{1,1}_0(V)$![]()
exists. Moreover for all $\psi \in C^\infty _c(V)$![]()

and $T= (f\partial _1\,h,\, \dots,\, f\partial _n h)$![]() satisfies the fine $\alpha$
satisfies the fine $\alpha$![]() -interpolation property (3.1) on $W^{1,1}_0(U)$
-interpolation property (3.1) on $W^{1,1}_0(U)$![]() with $C= c(U,\,V) \|f\|_{0,\alpha } [h]_{0,\alpha }$
with $C= c(U,\,V) \|f\|_{0,\alpha } [h]_{0,\alpha }$![]() .
.
Remark 3.9 If $h$![]() is merely in $C^{0,\alpha }(\overline U)$
is merely in $C^{0,\alpha }(\overline U)$![]() , a similar result holds true with the following estimates for all $\psi \in W^{1,1}_0(U)$
, a similar result holds true with the following estimates for all $\psi \in W^{1,1}_0(U)$![]() :
:

and
i.e. $T= (f\partial _1\,h,\, \dots,\, f\partial _n h)$![]() satisfies the $\alpha$
satisfies the $\alpha$![]() -interpolation property on $W^{1,1}_0(U)$
-interpolation property on $W^{1,1}_0(U)$![]() .
.
Proof. Let $\psi \in W^{1,1}_0(V)$![]() , and for $\varepsilon < {\rm dist}( \overline V,\, \partial U)$
, and for $\varepsilon < {\rm dist}( \overline V,\, \partial U)$![]() we define:
we define:
We first prove that $a^{(\varepsilon )}$![]() is a Cauchy sequence. For any $0<\varepsilon '<\varepsilon$
is a Cauchy sequence. For any $0<\varepsilon '<\varepsilon$![]() we have
we have

We estimate, using $\varepsilon '<\varepsilon$![]() :
:

where we used lemma 3.1-(i) and proposition 3.5 in the third line. For $I_3(\varepsilon,\, \varepsilon ')$![]() , we note that $\varepsilon \not \le \varepsilon '$
, we note that $\varepsilon \not \le \varepsilon '$![]() and hence the same estimate as for $I_1$
and hence the same estimate as for $I_1$![]() is not obtained, but through the same calculations as for $I_1$
is not obtained, but through the same calculations as for $I_1$![]() , we obtain
, we obtain
In the same manner, we can also obtain an estimate for $I_2$![]() :
:

Putting the three estimates together in view of (3.3), we obtain a first crude estimate:

This estimate is not enough to establish the Cauchy property of the sequence $a^{(\varepsilon )}$![]() . Therefore, we proceed as follows. If $\varepsilon '/\varepsilon \ge 1/2$
. Therefore, we proceed as follows. If $\varepsilon '/\varepsilon \ge 1/2$![]() , we set $\rho = \varepsilon '/\varepsilon$
, we set $\rho = \varepsilon '/\varepsilon$![]() , $m=1$
, $m=1$![]() . Otherwise there exists $m \in \mathbb {N}$
. Otherwise there exists $m \in \mathbb {N}$![]() , depending on $\varepsilon '/\varepsilon <1$
, depending on $\varepsilon '/\varepsilon <1$![]() , such that $1/4 \le \rho = ({\varepsilon '}/{\varepsilon })^{1/m} <1/2$
, such that $1/4 \le \rho = ({\varepsilon '}/{\varepsilon })^{1/m} <1/2$![]() . We now write
. We now write

We apply (3.4) successively to $0 <\rho ^{k}\varepsilon < \rho ^{k-1}\varepsilon$![]() (as the new $\varepsilon '$
(as the new $\varepsilon '$![]() and $\varepsilon$
and $\varepsilon$![]() ) to obtain
) to obtain

since by our choice either $1/2 \le \rho <1$![]() and $m=1$
and $m=1$![]() , or $1/4\le \rho <1/2$
, or $1/4\le \rho <1/2$![]() , independent of $\varepsilon ',\, \varepsilon$
, independent of $\varepsilon ',\, \varepsilon$![]() . This implies that $a^{(\varepsilon )}$
. This implies that $a^{(\varepsilon )}$![]() is Cauchy sequence. Hence, the limit
is Cauchy sequence. Hence, the limit
exists.
Now, we estimate for a fixed $\varepsilon >0$![]() , as $\varepsilon '\to 0$
, as $\varepsilon '\to 0$![]() :
:

which establishes (3.2). To obtain (3.1), applying lemma 3.1-(ii) and proposition 3.5 to $\partial _j h_\varepsilon$![]() we observe that:
we observe that:

In other words,

with $\delta _0 (1) = +\infty$![]() .
.
We conclude the proof of (3.1): Given, $\sigma >0$![]() , we let
, we let
Assume $\|\psi \|_{L^1} \le \delta \|\partial _j \psi \|_{L^1}$![]() for a given nonzero $\psi$
for a given nonzero $\psi$![]() , then letting
, then letting

we obtain $\varepsilon < {\rm dist} (\overline V,\, \partial U)$![]() by the Poincaré inequality $\|\psi \|_{L^1} \le {\rm diam}(V) \|\partial _j \psi \|_{L^1}$
by the Poincaré inequality $\|\psi \|_{L^1} \le {\rm diam}(V) \|\partial _j \psi \|_{L^1}$![]() on $V$
on $V$![]() . On the other hand we also have $\varepsilon \le \delta _0$
. On the other hand we also have $\varepsilon \le \delta _0$![]() and therefore applying (3.5) we obtain as required:
and therefore applying (3.5) we obtain as required:

Definition 3.10 We say $U \subset {\mathbb {R}}^n$![]() is an open coordinate rectangular box when it is a rectangular cuboid with edges parallel to the coordinate axes, i.e.
is an open coordinate rectangular box when it is a rectangular cuboid with edges parallel to the coordinate axes, i.e.

for $I_k$![]() an open interval in ${\mathbb {R}}$
an open interval in ${\mathbb {R}}$![]() .
.
Proposition 3.11 Assume that $U \subset {\mathbb {R}}^n$![]() is an open coordinate rectangular box and that for $f\in L^1(U)$
is an open coordinate rectangular box and that for $f\in L^1(U)$![]() , $T=\nabla f$
, $T=\nabla f$![]() satisfies the fine $\alpha$
satisfies the fine $\alpha$![]() -interpolation property on $W^{1,1}_0(U)$
-interpolation property on $W^{1,1}_0(U)$![]() according to definition 3.7 with $C=1$
according to definition 3.7 with $C=1$![]() . Then
. Then
In particular, by proposition 3.5, $f\in c^{0,\alpha } (\overline U)$![]() and $[f]_{0,\alpha ;U} \le 2^{n+1}.$
and $[f]_{0,\alpha ;U} \le 2^{n+1}.$![]()
Proof. The proof of the proposition follows classical ideas relating the decay of mean oscillations to pointwise behaviour of functions, as pioneered by Morrey and Campanato, see for instance [Reference Campanato8]. We prove the statement by induction over the dimension.
First let $n=1$![]() and $U \subset {\mathbb {R}}$
and $U \subset {\mathbb {R}}$![]() and be an open interval and let $I\subset U$
and be an open interval and let $I\subset U$![]() be any open subinterval. Note that for any $\phi \in C^\infty _c (I)$
be any open subinterval. Note that for any $\phi \in C^\infty _c (I)$![]() , we can construct a sequence $\tilde \phi _k \in C^\infty _c(I)$
, we can construct a sequence $\tilde \phi _k \in C^\infty _c(I)$![]() such that $\|\tilde \phi _k\|_{0}\le 1+ 2 \|\phi \|_{0}$
such that $\|\tilde \phi _k\|_{0}\le 1+ 2 \|\phi \|_{0}$![]() , and $\tilde \phi _k$
, and $\tilde \phi _k$![]() converges strongly in $L^1$
converges strongly in $L^1$![]() to $\phi - {\unicode{x2A0F}} _I \phi$
to $\phi - {\unicode{x2A0F}} _I \phi$![]() . Now fix $\varphi \in C^\infty _c(I)$
. Now fix $\varphi \in C^\infty _c(I)$![]() with ${\unicode{x2A0F}} _I \varphi =1$
with ${\unicode{x2A0F}} _I \varphi =1$![]() and let
and let

By the dominated convergence theorem we have
Let $\psi _k (t) = \int _{-\infty }^t \phi _k(s) {\rm d}s$![]() and note that $\psi _k \in C^\infty _c(I)$
and note that $\psi _k \in C^\infty _c(I)$![]() . We have therefore for all $\phi \in C^\infty _c(I)$
. We have therefore for all $\phi \in C^\infty _c(I)$![]() and $\sigma >0$
and $\sigma >0$![]() , provided $|I|\le \delta (\sigma )$
, provided $|I|\le \delta (\sigma )$![]() :
:

where we used the Poincaré inequality on $I$![]() . Since $(L^1)' = L^\infty$
. Since $(L^1)' = L^\infty$![]() , and $C^\infty _c(I)$
, and $C^\infty _c(I)$![]() is dense in $L^1(I)$
is dense in $L^1(I)$![]() , we conclude that
, we conclude that
Now, let $y\in U$![]() , and let $d= {\rm dist}(y,\, \partial U)$
, and let $d= {\rm dist}(y,\, \partial U)$![]() , and for $z\in (y-d/2,\, y+d/2)$
, and for $z\in (y-d/2,\, y+d/2)$![]() and $r< d/2$
and $r< d/2$![]() define
define
$h_r$![]() is continuous in $z$
is continuous in $z$![]() and converges a.e. to $f$
and converges a.e. to $f$![]() on $(y-d/2,\, y+d/2)$
on $(y-d/2,\, y+d/2)$![]() as $r\to 0$
as $r\to 0$![]() . On the other hand, for all $r'< r< d/2$
. On the other hand, for all $r'< r< d/2$![]() :
:

where we applied bound (3.6) to $I=(z-r,\, z+r)$![]() , $\sigma =1$
, $\sigma =1$![]() , $\delta (1)=+\infty$
, $\delta (1)=+\infty$![]() . As a consequence, $h_r$
. As a consequence, $h_r$![]() is a Cauchy sequence in the uniform norm and $f$
is a Cauchy sequence in the uniform norm and $f$![]() is continuous as the uniform limit of the $h_r$
is continuous as the uniform limit of the $h_r$![]() for $r \to 0$
for $r \to 0$![]() . Now, applying once again (3.6) to $I= (x,\,y) \subset U$
. Now, applying once again (3.6) to $I= (x,\,y) \subset U$![]() we obtain that
we obtain that
which implies $[f]_{0,\alpha ;U|\delta (\sigma )} \le 4 \sigma$![]() , as required.
, as required.
Now, assume that $n>1$![]() and that the statement is true for $n-1$
and that the statement is true for $n-1$![]() . Let $Q\subset U$
. Let $Q\subset U$![]() be any coordinate rectangular box, i.e.
be any coordinate rectangular box, i.e.

with the open intervals $I_k\subset {\mathbb {R}}$![]() . Let $\widehat {x}:= (x_1,\, \cdots,\, x_{n-1})$
. Let $\widehat {x}:= (x_1,\, \cdots,\, x_{n-1})$![]() and note that for all $h\in L^1(Q)$
and note that for all $h\in L^1(Q)$![]() ,
,

is well defined and belongs to $L^1(Q)$![]() . We claim that:
. We claim that:

Let us first show that the conclusion holds assuming claim (3.7) is true for all coordinate boxes $Q\subset U$![]() . For $a,\,b$
. For $a,\,b$![]() the extremities of $I_n$
the extremities of $I_n$![]() , choose $0 \le \theta _k \le 1$
, choose $0 \le \theta _k \le 1$![]() in $C^\infty _c (I_n)$
in $C^\infty _c (I_n)$![]() such that $\theta _k \equiv 1$
such that $\theta _k \equiv 1$![]() on $(a+1/k,\, b-1/k)$
on $(a+1/k,\, b-1/k)$![]() . Given $\sigma >0$
. Given $\sigma >0$![]() , for $1 \le j \le n-1$
, for $1 \le j \le n-1$![]() , and $\psi \in C^\infty _c (Q^{n-1})$
, and $\psi \in C^\infty _c (Q^{n-1})$![]() , assuming that $\|\psi \|_{L^1(Q^{n-1})} \le \delta (\sigma ) \|\partial _j \psi \|_{L^1(Q^{n-1})}$
, assuming that $\|\psi \|_{L^1(Q^{n-1})} \le \delta (\sigma ) \|\partial _j \psi \|_{L^1(Q^{n-1})}$![]() , we have by our main assumption on $f$
, we have by our main assumption on $f$![]() :
:

since $\theta _k \psi \in C^\infty _c(Q)$![]() and
and

Applying the induction assumption, we deduce that
To prove that $f$![]() is continuous, fix $y\in U$
is continuous, fix $y\in U$![]() and consider a box $Q_d = Q^{n-1} \times (y_n-d,\, y_n+d) \subset U$
and consider a box $Q_d = Q^{n-1} \times (y_n-d,\, y_n+d) \subset U$![]() containing $y$
containing $y$![]() . For all $z\in Q^{n-1} \times (y_n -d/2,\, y_n+ d/2)$
. For all $z\in Q^{n-1} \times (y_n -d/2,\, y_n+ d/2)$![]() , and $r< d/2$
, and $r< d/2$![]() we define
we define
Note that, if $r$![]() is fixed, the vertical averages of $f$
is fixed, the vertical averages of $f$![]() are continuous in $\widehat {z}$
are continuous in $\widehat {z}$![]() as established in (3.8), and so $h_r$
as established in (3.8), and so $h_r$![]() is continuous in $z$
is continuous in $z$![]() . Applying (3.7) with $\sigma =1$
. Applying (3.7) with $\sigma =1$![]() to $Q=Q^{n-1} \times (z_n -r,\, z_n+ r)$
to $Q=Q^{n-1} \times (z_n -r,\, z_n+ r)$![]() we have for $r'< r< d/2$
we have for $r'< r< d/2$![]() :
:

which implies that $h_r$![]() locally uniformly converge to their limit, which happens to be $f$
locally uniformly converge to their limit, which happens to be $f$![]() . Hence $f$
. Hence $f$![]() is continuous in $U$
is continuous in $U$![]() .
.
To obtain a Hölder estimate, let $x,\,y\in U$![]() . First, assume $x_j=y_j$
. First, assume $x_j=y_j$![]() for some $1 \le j\le n$
for some $1 \le j\le n$![]() . We re-arrange the coordinates so that $j=n$
. We re-arrange the coordinates so that $j=n$![]() and note that for any sequence of coordinate rectangular boxes $Q_k$
and note that for any sequence of coordinate rectangular boxes $Q_k$![]() of height $1/k$
of height $1/k$![]() , containing $x$
, containing $x$![]() and $y$
and $y$![]() , such that $x_n=y_n$
, such that $x_n=y_n$![]() is the midpoint of $I_{n,k}$
is the midpoint of $I_{n,k}$![]() , we have by (3.8)
, we have by (3.8)

If, on the other hand, $x_j\neq y_j$![]() for all $j$
for all $j$![]() , we can choose a coordinate rectangular box $Q\subset U$
, we can choose a coordinate rectangular box $Q\subset U$![]() which has $x$
which has $x$![]() and $y$
and $y$![]() as its opposite vertices on the largest diameter. We obtain by applying (3.7) and (3.8) to the now continuous $f$
as its opposite vertices on the largest diameter. We obtain by applying (3.7) and (3.8) to the now continuous $f$![]() , provided $|x-y| \le \delta (\sigma )$
, provided $|x-y| \le \delta (\sigma )$![]() :
:

In both cases we can conclude with the desired bound, i.e. $[f]_{0,\alpha ; U |\delta (\sigma )} \le 2^{n+1}\sigma$![]() . Note that the sequence $Q_k$
. Note that the sequence $Q_k$![]() in the first case and the box $Q$
in the first case and the box $Q$![]() in the second case exist since $U$
in the second case exist since $U$![]() is assumed to be a coordinate box itself.
is assumed to be a coordinate box itself.
It remains to prove claim (3.7). Given $\sigma >0$![]() assume that $|I_n|\le \delta (\sigma )$
assume that $|I_n|\le \delta (\sigma )$![]() as required in (3.7). For any $\phi \in C^\infty _c (Q)$
as required in (3.7). For any $\phi \in C^\infty _c (Q)$![]() , consider a sequence $\tilde \phi _k \in C^\infty _c(Q)$
, consider a sequence $\tilde \phi _k \in C^\infty _c(Q)$![]() , $\|\tilde \phi _k\|_0 \le 1 + 2\|\phi \|_0$
, $\|\tilde \phi _k\|_0 \le 1 + 2\|\phi \|_0$![]() , converging strongly in $L^1$
, converging strongly in $L^1$![]() to $\phi - \hat \phi (\widehat {x})$
to $\phi - \hat \phi (\widehat {x})$![]() . As a consequence,
. As a consequence,
Choose a $\varphi \in C^\infty _c(I_n)$![]() such that ${\unicode{x2A0F}} _{I_n} \varphi =1$
such that ${\unicode{x2A0F}} _{I_n} \varphi =1$![]() and define
and define

Then $\phi _k \in C^\infty _c(Q)$![]() converges in $L^1$
converges in $L^1$![]() to $\phi - \hat \phi (\widehat {x})$
to $\phi - \hat \phi (\widehat {x})$![]() and $\hat \phi _k (\widehat {x}) = {\unicode{x2A0F}} _{I_n} \phi _k(x) {\rm d}x_n =0$
and $\hat \phi _k (\widehat {x}) = {\unicode{x2A0F}} _{I_n} \phi _k(x) {\rm d}x_n =0$![]() . Letting $\psi _k (\widehat {x},\, t) = \int _{-\infty }^t \phi _k(\widehat {x},\, s) {\rm d}s$
. Letting $\psi _k (\widehat {x},\, t) = \int _{-\infty }^t \phi _k(\widehat {x},\, s) {\rm d}s$![]() we obtain for all $\phi \in C^\infty _c (Q)$
we obtain for all $\phi \in C^\infty _c (Q)$![]() , $\psi _k \in C^\infty _c(Q)$
, $\psi _k \in C^\infty _c(Q)$![]() . We hence obtain
. We hence obtain

where we used the Poincaré inequality
on $I_n$![]() . Once again, using the fact that $L^\infty$
. Once again, using the fact that $L^\infty$![]() is the dual of $L^1$
is the dual of $L^1$![]() , and the density of $C^\infty _c(Q)$
, and the density of $C^\infty _c(Q)$![]() in $L^1(Q)$
in $L^1(Q)$![]() , we conclude with (3.7).
, we conclude with (3.7).
4. A second fundamental form for $c^{1,\alpha }$ isometries
isometries
Let u$\in c^{1,\alpha }(\Omega,\, {\mathbb {R}}^3)$![]() be an immersion with $2/3 \le \alpha < 1$
be an immersion with $2/3 \le \alpha < 1$![]() and let $V \Subset \Omega$
and let $V \Subset \Omega$![]() be any smooth simply connected domain compactly contained in $\Omega$
be any smooth simply connected domain compactly contained in $\Omega$![]() , e.g. an open disk. We intend to show the following three statements, which we will formulate more precisely later on. We shall prove:
, e.g. an open disk. We intend to show the following three statements, which we will formulate more precisely later on. We shall prove:
1. A weak notion of the second fundamental form $A_{ij}= -\partial _i u \cdot \partial _j \vec n$
 makes sense for the immersion $u$
makes sense for the immersion $u$ on $V$
on $V$ . $A=[A_{ij}]$
. $A=[A_{ij}]$ is symmetric. This part can be carried out for $\alpha >1/2$
is symmetric. This part can be carried out for $\alpha >1/2$ .
.2. If $u$
 is isometric, then $A$
is isometric, then $A$ is curl free, and is equal to $\nabla ^2 v$
is curl free, and is equal to $\nabla ^2 v$ for a scalar function $v\in c^{1,\alpha }(V)$
for a scalar function $v\in c^{1,\alpha }(V)$ .
.3. $\displaystyle {\mathcal {D}et}\, (D^2 v) = -1/2 {\rm curl}^T {\rm curl}\, (\nabla v \otimes \nabla v)=0$
 in $\mathcal {D}'(V)$
in $\mathcal {D}'(V)$ .
.
We choose an open smooth domain $U$![]() such that $V \Subset U \Subset \Omega$
such that $V \Subset U \Subset \Omega$![]() . Let $\phi \in C^\infty _c (B(0,\,1))$
. Let $\phi \in C^\infty _c (B(0,\,1))$![]() be a nonnegative function with $\int \phi =1$
be a nonnegative function with $\int \phi =1$![]() . For $\varepsilon < {\rm dist}(\overline V,\, \partial U)$
. For $\varepsilon < {\rm dist}(\overline V,\, \partial U)$![]() we define
we define
to be the mollification of the unit normal
of immersion $u$![]() . Note that by assumption $C_0:= \|\partial _1 u \times \partial _2 u\|_{0;U}>0$
. Note that by assumption $C_0:= \|\partial _1 u \times \partial _2 u\|_{0;U}>0$![]() and $\vec n \in c^{0,\alpha } (\Omega,\,{\mathbb {R}}^3)$
and $\vec n \in c^{0,\alpha } (\Omega,\,{\mathbb {R}}^3)$![]() . Let $u_\varepsilon := u \ast \phi _\varepsilon : V\to {\mathbb {R}}^3$
. Let $u_\varepsilon := u \ast \phi _\varepsilon : V\to {\mathbb {R}}^3$![]() be the standard mollification of $u$
be the standard mollification of $u$![]() on $V$
on $V$![]() . If $\varepsilon$
. If $\varepsilon$![]() is small enough $u_\varepsilon$
is small enough $u_\varepsilon$![]() is an immersion since $\nabla u_\varepsilon$
is an immersion since $\nabla u_\varepsilon$![]() converges uniformly to $\nabla u$
converges uniformly to $\nabla u$![]() on $V$
on $V$![]() , and
, and
We define
to be the unit normal corresponding to $u_\varepsilon$![]() . A direct application of lemma 3.1 yields:
. A direct application of lemma 3.1 yields:

We also note that
To see the first estimate we observe that

where we used (4.1). The second estimate also follows from (4.1) and a direct calculation.
We finally denote by the symmetric matrix field $A^{\varepsilon } :=[A^\varepsilon _{ij}]$![]() the second fundamental form associated with the immersion $u_\varepsilon$
the second fundamental form associated with the immersion $u_\varepsilon$![]() in the local coordinates, i.e.
in the local coordinates, i.e.
which by (4.1) satisfies the obvious bound
4.1. Definition of the second fundamental form $A$
We are ready now to prove our main claims about the existence of a second fundamental form for the immersion $u$![]() and its properties. In what follows the constant $C=c(U,\, V,\, \|u\|_{1,\alpha ;U},\, C_0)$
and its properties. In what follows the constant $C=c(U,\, V,\, \|u\|_{1,\alpha ;U},\, C_0)$![]() might change but it has a universal upper bound only depending on the stated quantities.
might change but it has a universal upper bound only depending on the stated quantities.
Proposition 4.1 If $\alpha > 1/2$![]() , then $A^{\varepsilon }_{ij}$
, then $A^{\varepsilon }_{ij}$![]() converges in the sense of distributions to a distribution $A_{ij} \in \mathcal {D}'(V)$
converges in the sense of distributions to a distribution $A_{ij} \in \mathcal {D}'(V)$![]() . More precisely, the convergence is in the dual of $W^{1,1}_0(V)$
. More precisely, the convergence is in the dual of $W^{1,1}_0(V)$![]() , and we have:
, and we have:

Moreover, for each $i$![]() , the distribution $T=(A_{ij})_{j=1}^n$
, the distribution $T=(A_{ij})_{j=1}^n$![]() satisfies the fine $\alpha$
satisfies the fine $\alpha$![]() -interpolation property on $W^{1,1}_0(V)$
-interpolation property on $W^{1,1}_0(V)$![]() according to definition 3.7.
according to definition 3.7.
Proof. Applying proposition 3.8 to the components $f:= \partial _i u^m$![]() , $h:= \vec n^m$
, $h:= \vec n^m$![]() , for $m\in \{1,\,2,\,3\}$
, for $m\in \{1,\,2,\,3\}$![]() , we deduce that for a distribution $A_{ij} \in \mathcal {D'}(V)$
, we deduce that for a distribution $A_{ij} \in \mathcal {D'}(V)$![]() ,
,
and

On the other hand, we have for all $\psi \in W^{1,1}_0(V)$![]() :
:

where we used proposition 3.8, (4.1) and (4.2). The stated fine $\alpha$![]() -interpolation property follows as in proposition 3.8.
-interpolation property follows as in proposition 3.8.
Definition 4.2 For $1/2 < \alpha <1$![]() , we define the weak second fundamental form of an immersion $u\in c^{1,\alpha }(\Omega,\, {\mathbb {R}}^3)$
, we define the weak second fundamental form of an immersion $u\in c^{1,\alpha }(\Omega,\, {\mathbb {R}}^3)$![]() on $V$
on $V$![]() as the distribution
as the distribution
Remark 4.3 The definition of $A$![]() can be uniquely extended to a distribution globally defined on $\Omega$
can be uniquely extended to a distribution globally defined on $\Omega$![]() , i.e. belonging to $\mathcal {D}'(\Omega,\, {\mathbb {R}}_{sym}^{2\times 2})$
, i.e. belonging to $\mathcal {D}'(\Omega,\, {\mathbb {R}}_{sym}^{2\times 2})$![]() , but we will not need this fact.
, but we will not need this fact.
4.2. $A$ satisfies Gauss-Codazzi-Mainardi equations (in a weak sense)
satisfies Gauss-Codazzi-Mainardi equations (in a weak sense)
From now on we assume that the immersion $u$![]() is also isometric, i.e. the pull back-metric $g:= (\nabla u)^T (\nabla u)$
is also isometric, i.e. the pull back-metric $g:= (\nabla u)^T (\nabla u)$![]() is the Euclidean metric $\mathscr {E}_2$
is the Euclidean metric $\mathscr {E}_2$![]() on $\Omega$
on $\Omega$![]() . We consider $\mathscr {G}^{\varepsilon }:= (\nabla u_\varepsilon )^T \nabla u_\varepsilon = u_\varepsilon ^\ast \mathscr {E}_3$
. We consider $\mathscr {G}^{\varepsilon }:= (\nabla u_\varepsilon )^T \nabla u_\varepsilon = u_\varepsilon ^\ast \mathscr {E}_3$![]() , the pull-back metric induced by $u_\varepsilon$
, the pull-back metric induced by $u_\varepsilon$![]() , where $\mathscr {E}_3$
, where $\mathscr {E}_3$![]() is the Euclidean metric of ${\mathbb {R}}^3$
is the Euclidean metric of ${\mathbb {R}}^3$![]() . The commutator estimate lemma 3.1-(iii) implies
. The commutator estimate lemma 3.1-(iii) implies
So, in view of the fact that $\mathscr {E}_2\ast \phi _\varepsilon = \mathscr {E}_2$![]() on $V$
on $V$![]() we obtain:
we obtain:
Compare with [Reference Conti, De Lellis and Székelyhidi13, Proposition 1], which is stated under more general settings and where the mollifier needs to be symmetric.
Proposition 4.4 We have the uniform estimate
In particular, if $\alpha \ge 2/3$![]() , then ${\rm curl} \, A =0$
, then ${\rm curl} \, A =0$![]() in $\mathcal {D}'(V)$
in $\mathcal {D}'(V)$![]() .
.
Proof. We recall that the Christoffel symbols associated with a metric $g$![]() are given by
are given by
where the Einstein summation convention is used. Hence, in view of (4.5), we have
uniformly, if $\alpha \ge 1/2$![]() , with the estimate
, with the estimate
Writing the Codazzi–Mainardi equations [Reference Han and Hong27, Equation (2.1.6)] for the immersion $u_\varepsilon$![]() we have
we have

which completes the proof.
Before proceeding to the next step, we need to establish a further property of the sequence $A^\varepsilon$![]() . Observe that if $u \in C^2(\Omega,\, {\mathbb {R}}^3)$
. Observe that if $u \in C^2(\Omega,\, {\mathbb {R}}^3)$![]() were an isometric immersion, then the determinant of its second fundamental form $A$
were an isometric immersion, then the determinant of its second fundamental form $A$![]() would vanish, since, in this particular case, it would be equal to the Gaussian curvature of the Euclidean metric. In the case considered here, $u$
would vanish, since, in this particular case, it would be equal to the Gaussian curvature of the Euclidean metric. In the case considered here, $u$![]() does not enjoy the sufficient regularity for $\det A$
does not enjoy the sufficient regularity for $\det A$![]() to be defined. However, we can show that for $\alpha \ge 1/2$
to be defined. However, we can show that for $\alpha \ge 1/2$![]() , $\det A^\varepsilon$
, $\det A^\varepsilon$![]() converges in the sense of distributions to $0$
converges in the sense of distributions to $0$![]() as $\varepsilon \to 0$
as $\varepsilon \to 0$![]() , that with a rate which will be crucial in our analysis. The following statement is a slight variant of [Reference Conti, De Lellis and Székelyhidi13, Proposition 7] recast for our purposes:
, that with a rate which will be crucial in our analysis. The following statement is a slight variant of [Reference Conti, De Lellis and Székelyhidi13, Proposition 7] recast for our purposes:
Proposition 4.5 Let $A^\varepsilon$![]() be as defined in (4.3). Then for all $\psi \in C^\infty _c(V)$
be as defined in (4.3). Then for all $\psi \in C^\infty _c(V)$![]() ,
,

Proof. In view of the formula for the $(0,\,4)$![]() -Riemann curvature tensor [Reference Han and Hong27, Equation (2.1.2)]
-Riemann curvature tensor [Reference Han and Hong27, Equation (2.1.2)]
and by the Gauss equation [Reference Han and Hong27, Equation (2.1.7)], (4.5) and (4.7) we have on $V$![]() :
:

The conclusion follows by an integration by parts involving the first term and applying (4.5).
4.3. $A$ as the Hessian of a scalar function
as the Hessian of a scalar function
Proposition 4.6 Let $\alpha \ge 2/3$![]() , $u\in c^{1,\alpha }(\Omega,\, {\mathbb {R}}^3)$
, $u\in c^{1,\alpha }(\Omega,\, {\mathbb {R}}^3)$![]() be an isometric immersion and $V$
be an isometric immersion and $V$![]() be a smooth simply connected domain compactly contained in $\Omega$
be a smooth simply connected domain compactly contained in $\Omega$![]() . There exists $v\in c^{1,\alpha } (V) \cap W^{1,2}(V)$
. There exists $v\in c^{1,\alpha } (V) \cap W^{1,2}(V)$![]() such that $A$
such that $A$![]() , the second fundamental form of $u$
, the second fundamental form of $u$![]() on $V$
on $V$![]() , equals $\nabla ^2 v$
, equals $\nabla ^2 v$![]() in the sense of distributions. Moreover
in the sense of distributions. Moreover
Remark 4.7 In our setting, it can also be shown that $v\in c^{1,\alpha }(\overline V)$![]() . In view of remark 4.3, one can find such $v\in c^{1, \alpha }(\Omega )$
. In view of remark 4.3, one can find such $v\in c^{1, \alpha }(\Omega )$![]() provided $\Omega$
provided $\Omega$![]() is simply connected. We will not need these facts.
is simply connected. We will not need these facts.
Proof. Let $A^{\varepsilon }$![]() be as defined in (4.3) and let $F^\varepsilon$
be as defined in (4.3) and let $F^\varepsilon$![]() be the solution to the Neumann problem
be the solution to the Neumann problem
Since ${\rm div} (\nabla F^\varepsilon - A^{\varepsilon }) =0$![]() , there exists a vector field $E^\varepsilon$
, there exists a vector field $E^\varepsilon$![]() such that $A^\varepsilon = \nabla F^\varepsilon + \nabla ^\perp E^\varepsilon$
such that $A^\varepsilon = \nabla F^\varepsilon + \nabla ^\perp E^\varepsilon$![]() . $E^\varepsilon$
. $E^\varepsilon$![]() solves
solves
Since $A^\varepsilon$![]() is symmetric, we have $\partial _2 (F_1^\varepsilon + E_2^\varepsilon ) = \partial _1 (F_2^\varepsilon - E_1^\varepsilon )$
is symmetric, we have $\partial _2 (F_1^\varepsilon + E_2^\varepsilon ) = \partial _1 (F_2^\varepsilon - E_1^\varepsilon )$![]() , and thus we derive the existence of a scalar function $v^{(\varepsilon )} \in C^\infty (V)$
, and thus we derive the existence of a scalar function $v^{(\varepsilon )} \in C^\infty (V)$![]() satisfying
satisfying
i.e. $\nabla v^{(\varepsilon )} = F^\varepsilon + (E_1^\varepsilon,\, -E_2^\varepsilon )$![]() . As a consequence
. As a consequence
Standard elliptic estimates imply that for any $p<\infty$![]()
As a consequence, fixing $p>2$![]() , and in view of (4.6), $\|A^\varepsilon - \nabla ^2 v^{(\varepsilon )}\|_{0;V} \le C o(\varepsilon ^{3\alpha -2}) \to 0$
, and in view of (4.6), $\|A^\varepsilon - \nabla ^2 v^{(\varepsilon )}\|_{0;V} \le C o(\varepsilon ^{3\alpha -2}) \to 0$![]() and therefore $\nabla ^2 v^{(\varepsilon )}$
and therefore $\nabla ^2 v^{(\varepsilon )}$![]() converges to $A$
converges to $A$![]() in the sense of distributions.
in the sense of distributions.
Now, for all $\varphi \in C^\infty _c (V)$![]() , there exists a vector field $\Psi$
, there exists a vector field $\Psi$![]() in $V$
in $V$![]() , vanishing on $\partial V$
, vanishing on $\partial V$![]() , such that ${\rm div} \, \Psi = \varphi - {\unicode{x2A0F}} _V \varphi$
, such that ${\rm div} \, \Psi = \varphi - {\unicode{x2A0F}} _V \varphi$![]() , for which $\|\Psi \|_{W^{1,2}(V)} \le c(V) \|\varphi \|_{L^2(V)}$
, for which $\|\Psi \|_{W^{1,2}(V)} \le c(V) \|\varphi \|_{L^2(V)}$![]() (see e.g. [Reference Arnold, Scott and Vogelius1]). By adjusting the $\nabla v^{(\varepsilon )}$
(see e.g. [Reference Arnold, Scott and Vogelius1]). By adjusting the $\nabla v^{(\varepsilon )}$![]() so that it is of average 0 over $V$
so that it is of average 0 over $V$![]() , and in view of proposition 4.1, we obtain that for all $\varepsilon,\, \varepsilon ' \le \delta$
, and in view of proposition 4.1, we obtain that for all $\varepsilon,\, \varepsilon ' \le \delta$![]() :
:

By duality, we conclude that $\nabla v^{(\varepsilon )}$![]() converges strongly in $L^2(V)$
converges strongly in $L^2(V)$![]() to a vector field $F$
to a vector field $F$![]() and that $\nabla F = A$
and that $\nabla F = A$![]() . It is now straightforward to see that, if necessary by adjusting the $v^{(\varepsilon )}$
. It is now straightforward to see that, if necessary by adjusting the $v^{(\varepsilon )}$![]() by constants, $v^{(\varepsilon )}$
by constants, $v^{(\varepsilon )}$![]() converges strongly in $W^{1,2}$
converges strongly in $W^{1,2}$![]() to some $v\in W^{1,2}(V)$
to some $v\in W^{1,2}(V)$![]() and that $A= \nabla ^2 v$
and that $A= \nabla ^2 v$![]() .
.
To complete the proof, it is only necessary to show that (a) ${\mathcal {D}et}\, D^2 v =0$![]() and (b) $v\in c^{1,\alpha }(V)$
and (b) $v\in c^{1,\alpha }(V)$![]() .
.
In order to show (a), we first observe that since $\nabla v^{(\varepsilon )} \to \nabla v$![]() in $L^2(V)$
in $L^2(V)$![]() , for all $\psi \in C^\infty _c(V)$
, for all $\psi \in C^\infty _c(V)$![]() we obtain:
we obtain:

The third term obviously converges to $0$![]() , and so does the first term by proposition 4.5. For the second term, we have, using propositions 4.1, (4.6) and (4.8)
, and so does the first term by proposition 4.5. For the second term, we have, using propositions 4.1, (4.6) and (4.8)

This completes the proof of (a).
It remains to prove (b) $v\in c^{1,\alpha }(V)$![]() . Since $\nabla ^2 v =A$
. Since $\nabla ^2 v =A$![]() is symmetric in $i,\,j$
is symmetric in $i,\,j$![]() , we have $\partial _{ji} v = \partial _{ij}v = A_{ij}$
, we have $\partial _{ji} v = \partial _{ij}v = A_{ij}$![]() , as distributions. Proposition 4.1 implies that, for each $i$
, as distributions. Proposition 4.1 implies that, for each $i$![]() , $\nabla (\partial _i v)$
, $\nabla (\partial _i v)$![]() satisfies the fine $\alpha$
satisfies the fine $\alpha$![]() -interpolation inequality on $W^{1,1}_0(V)$
-interpolation inequality on $W^{1,1}_0(V)$![]() . For any $x\in V$
. For any $x\in V$![]() , we apply proposition 3.11 to a coordinate rectangular box containing $x$
, we apply proposition 3.11 to a coordinate rectangular box containing $x$![]() and compactly included in $V$
and compactly included in $V$![]() to conclude that $\partial _i v \in c^{0,\alpha } (V)$
to conclude that $\partial _i v \in c^{0,\alpha } (V)$![]() for $i=1,\,2$
for $i=1,\,2$![]() , which yields $v\in c^{1,\alpha }(V)$
, which yields $v\in c^{1,\alpha }(V)$![]() .
.
5. Developability: a proof of theorem 1.3
Let $u\in c^{1,\alpha }(\Omega,\, {\mathbb {R}}^3)$![]() be an isometric immersion for $2/3 \le \alpha <1$
be an isometric immersion for $2/3 \le \alpha <1$![]() . In order to prove our main theorem, and in view of proposition 2.1, it is sufficient to show that $\nabla u$
. In order to prove our main theorem, and in view of proposition 2.1, it is sufficient to show that $\nabla u$![]() satisfies condition (c). We first fix an open disk $V$
satisfies condition (c). We first fix an open disk $V$![]() containing $x$
containing $x$![]() and compactly contained in $\Omega$
and compactly contained in $\Omega$![]() and note the existence of the function $v\in c^{1,\alpha }(V) \subset c^{1,2/3}(V)$
and note the existence of the function $v\in c^{1,\alpha }(V) \subset c^{1,2/3}(V)$![]() as defined in proposition 4.6. We apply the key developability result theorem 1.5 to $v$
as defined in proposition 4.6. We apply the key developability result theorem 1.5 to $v$![]() to obtain that $\nabla v$
to obtain that $\nabla v$![]() satisfies any of the equivalent conditions of proposition 2.1 in $V$
satisfies any of the equivalent conditions of proposition 2.1 in $V$![]() . The developability of $u$
. The developability of $u$![]() is a consequence of corollory 2.2 and proposition 5.1 below. The second conclusion follows from corollary 3.6.
is a consequence of corollory 2.2 and proposition 5.1 below. The second conclusion follows from corollary 3.6.
Proposition 5.1 Let $1/2 < \alpha <1$![]() and $u\in c^{1,\alpha }(\Omega,\, {\mathbb {R}}^3)$
and $u\in c^{1,\alpha }(\Omega,\, {\mathbb {R}}^3)$![]() be an immersion, with the second fundamental form $A$
be an immersion, with the second fundamental form $A$![]() defined as in proposition 4.1 on $V \Subset \Omega$
defined as in proposition 4.1 on $V \Subset \Omega$![]() . Assume moreover that $A= \nabla ^2 v$
. Assume moreover that $A= \nabla ^2 v$![]() , where $v\in C^1(V)$
, where $v\in C^1(V)$![]() . Then $u|_V$
. Then $u|_V$![]() is developable if and only if $v$
is developable if and only if $v$![]() is developable.
is developable.
Proof. We consider the following identity [Reference Han and Hong27, Equation (2.1.3)] (also known as the Gauss equation in the literature), which is valid for the mollified sequence of smooth immersions $u_\varepsilon$![]() :
:
where the standard Einstein summation convention is used.
Let $B\subset V$![]() be a given disk, $\psi \in C^\infty _c(B)$
be a given disk, $\psi \in C^\infty _c(B)$![]() and Lipschitz unit vector field $\vec \eta : B \to {\mathbb {R}}^2$
and Lipschitz unit vector field $\vec \eta : B \to {\mathbb {R}}^2$![]() . We denote the coefficients of $u$
. We denote the coefficients of $u$![]() and $N^\varepsilon$
and $N^\varepsilon$![]() respectively by $u^m$
respectively by $u^m$![]() and $N^{\varepsilon, m}$
and $N^{\varepsilon, m}$![]() and calculate for $m=1,\,2,\,3$
and calculate for $m=1,\,2,\,3$![]() ,
,

where we used (4.7). We have

By proposition 4.1 we have:

where we used (4.2). Note also that in view of $A= \nabla ^2 v$![]() , we have for all $\varepsilon$
, we have for all $\varepsilon$![]() , in view of the fact that $N^{\varepsilon,m} \psi \in C^\infty _c(B)$
, in view of the fact that $N^{\varepsilon,m} \psi \in C^\infty _c(B)$![]() :
:
Therefore, (5.2) implies
If $v$![]() is developable, we apply corollary 2.10 to $\nabla v$
is developable, we apply corollary 2.10 to $\nabla v$![]() , and choose accordingly the open disk $B$
, and choose accordingly the open disk $B$![]() around $x\in V$
around $x\in V$![]() and the Lipschitz unit vector field $\vec \eta : B \to {\mathbb {R}}^2$
and the Lipschitz unit vector field $\vec \eta : B \to {\mathbb {R}}^2$![]() . Therefore,
. Therefore,
We apply lemma 2.11 to $f=\nabla v$![]() and $B= B_x$
and $B= B_x$![]() to obtain for any $\psi \in C^\infty _c(B)$
to obtain for any $\psi \in C^\infty _c(B)$![]() :
:
where we used the fact that $N^{\varepsilon,m} \psi \in C^\infty _c(B)$![]() . By (5.3) we conclude that
. By (5.3) we conclude that
Once again applying lemma 2.11 and (5.4) implies that the Jacobian derivative $\nabla u$![]() of the isometric immersion $u$
of the isometric immersion $u$![]() is constant along the segments generated by the vector field $\vec \eta$
is constant along the segments generated by the vector field $\vec \eta$![]() in $B$
in $B$![]() . Therefore, $\nabla u$
. Therefore, $\nabla u$![]() satisfies condition (c) of proposition 2.1, which implies the developability of $u|_V$
satisfies condition (c) of proposition 2.1, which implies the developability of $u|_V$![]() . As already mentioned, this part of the proof concludes the proof of theorem 1.3 for $u\in c^{1,\alpha }$
. As already mentioned, this part of the proof concludes the proof of theorem 1.3 for $u\in c^{1,\alpha }$![]() , $2/3 \le \alpha <1$
, $2/3 \le \alpha <1$![]() .
.
To finish the proof of proposition 5.1 we need to prove the converse statement. If, on the other hand, $u|_V$![]() is assumed to be developable, we proceed in a similar manner. According to corollary 2.10 and lemma 2.11, for all $x\in V$
is assumed to be developable, we proceed in a similar manner. According to corollary 2.10 and lemma 2.11, for all $x\in V$![]() there exist a disk $B\subset V$
there exist a disk $B\subset V$![]() centred at $x$
centred at $x$![]() and a unit Lipschitz vector field $\vec \eta : B \to {\mathbb {R}}^2$
and a unit Lipschitz vector field $\vec \eta : B \to {\mathbb {R}}^2$![]() such that for all $\psi \in C^\infty _c(B)$
such that for all $\psi \in C^\infty _c(B)$![]() :
:
Hence, using the fact that $A_{ij}^\varepsilon = \partial _{ij} u_\varepsilon \cdot N^\varepsilon$![]() we deduce for all $\psi \in C^\infty _c(B)$
we deduce for all $\psi \in C^\infty _c(B)$![]() :
:

where we used (4.1) and (4.2) to obtain a convergence of order $o(\varepsilon ^{2\alpha -1})$![]() in the last line. Following the same line of argument as before $v$
in the last line. Following the same line of argument as before $v$![]() is hence developable in view of lemma 2.11.
is hence developable in view of lemma 2.11.
Acknowledgements
This project was based upon work supported by the National Science Foundation and was partially funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation). M. R. P. was supported by the NSF award DMS-1813738 and by the DFG via SFB 1060—project Id 211504053. The second author would like to personally thank Stefan Müller for the opportunity to work at IAM, University of Bonn, Germany, where part of this work was completed, and for his kind support.
Appendix A. Developabiltiy of each component can be shown independently
Proposition A.1 Assume $\Omega \subset {\mathbb {R}}^2$![]() is an arbitrary domain, $2/3 \le \alpha <1$
is an arbitrary domain, $2/3 \le \alpha <1$![]() and let $u\in c^{1, \alpha } (\Omega,\, {\mathbb {R}}^3)$
and let $u\in c^{1, \alpha } (\Omega,\, {\mathbb {R}}^3)$![]() be an isometric immersion. Then for each $m=1,\,2,\,3$
be an isometric immersion. Then for each $m=1,\,2,\,3$![]() , the component $u^m$
, the component $u^m$![]() is developable in $\Omega$
is developable in $\Omega$![]() .
.
Remark A.2 Obviously this statement does not guarantee that the constancy lines or regions of $\nabla u^m$![]() are the same for the three components. If this fact is independently shown (e.g. through geometric arguments) theorem 1.3 will also be proved through this approach.
are the same for the three components. If this fact is independently shown (e.g. through geometric arguments) theorem 1.3 will also be proved through this approach.
Proof. In view of thereom 1.5, it suffices to show that ${\mathcal {D}et}\, D^2 u^m=0$![]() for each $m$
for each $m$![]() . Once again, we consider the mollifications $u_\varepsilon = u\ast \phi _\varepsilon$
. Once again, we consider the mollifications $u_\varepsilon = u\ast \phi _\varepsilon$![]() defined on a suitably chosen domain $V\Subset \Omega$
defined on a suitably chosen domain $V\Subset \Omega$![]() and use (5.1) to calculate for m=1,2,3 and $\psi \in C^\infty _c(V)$
and use (5.1) to calculate for m=1,2,3 and $\psi \in C^\infty _c(V)$![]() :
:

The second term obviously converges to $0$![]() in view of (4.7). For the third term we use (4.1), (4.4) and (4.7) to prove:
in view of (4.7). For the third term we use (4.1), (4.4) and (4.7) to prove:

Finally, the vanishing of the first term follows from Propostion 4.5 and (4.2) since

□
Appendix B. Little Hölder spaces and modulus of continuity
Here we will prove two auxiliary statements regarding little Hölder spaces.
Lemma B.1 Let $V\subset U\subset {\mathbb {R}}^n$![]() be open sets such that ${\rm dist}{(\overline V,\, \partial U)} >0$
be open sets such that ${\rm dist}{(\overline V,\, \partial U)} >0$![]() and $f: U\to {\mathbb {R}}$
and $f: U\to {\mathbb {R}}$![]() . If for $0<\alpha <1$
. If for $0<\alpha <1$![]() , $[f]_{0,\alpha ;U|r}$
, $[f]_{0,\alpha ;U|r}$![]() is $o(1)$
is $o(1)$![]() as a function of $r$
as a function of $r$![]() , then $\|f_\varepsilon - f\|_{0,\alpha ;V}\to 0$
, then $\|f_\varepsilon - f\|_{0,\alpha ;V}\to 0$![]() as $\varepsilon \to 0$
as $\varepsilon \to 0$![]() .
.
Proof. Let $\varepsilon < {\rm dist}{(\overline V,\, \partial U)}$![]() . We first note that by lemma 3.1-(i) we have
. We first note that by lemma 3.1-(i) we have
We therefore estimate

We now observe that

Combining the latter two estimates we hence obtain
In view of (B.1) and the main assumption, we conclude with the desired approximation of $f$![]() by $f_\varepsilon \in C^\infty (\overline V)$
by $f_\varepsilon \in C^\infty (\overline V)$![]() in $C^{0,\alpha }$
in $C^{0,\alpha }$![]() .
.
Proposition B.2 Let $U\subset {\mathbb {R}}^n$![]() be a bounded weakly Lipschitz domain and let $f: U \to {\mathbb {R}}$
be a bounded weakly Lipschitz domain and let $f: U \to {\mathbb {R}}$![]() be uniformly continuous. Then $f$
be uniformly continuous. Then $f$![]() admits an extension $\tilde f: {\mathbb {R}}^n \to {\mathbb {R}}$
admits an extension $\tilde f: {\mathbb {R}}^n \to {\mathbb {R}}$![]() with $\omega _{\tilde f;{\mathbb {R}}^n}\le c(U) \omega _{f;U}$
with $\omega _{\tilde f;{\mathbb {R}}^n}\le c(U) \omega _{f;U}$![]() .
.
Proof. $U$![]() is a bounded weakly Lipschitz domain, i.e. by the standard definition, there is a covering of $\overline U$
is a bounded weakly Lipschitz domain, i.e. by the standard definition, there is a covering of $\overline U$![]() of open sets $U_i$
of open sets $U_i$![]() and charts $\psi _i: U_i \to {\mathbb {R}}^n$
and charts $\psi _i: U_i \to {\mathbb {R}}^n$![]() , $0\le i\le N$
, $0\le i\le N$![]() such that $U_0 \subset U$
such that $U_0 \subset U$![]() and for $0 \le i\le N$
and for $0 \le i\le N$![]() , $\psi _i$
, $\psi _i$![]() is a bilipschitz diffeomorphism between $U_i$
is a bilipschitz diffeomorphism between $U_i$![]() and an open cylinder $V_i:= B_i \times (-1,\,1) \subset {\mathbb {R}}^n$
and an open cylinder $V_i:= B_i \times (-1,\,1) \subset {\mathbb {R}}^n$![]() such that $\psi _i(U\cap U_i)= V_i^+ := B_i \times (0,\,1)$
such that $\psi _i(U\cap U_i)= V_i^+ := B_i \times (0,\,1)$![]() and $\psi _i (\partial U \cap U_i) = B_i \times \{0\}$
and $\psi _i (\partial U \cap U_i) = B_i \times \{0\}$![]() , where $B_i \subset {\mathbb {R}}^{n-1}$
, where $B_i \subset {\mathbb {R}}^{n-1}$![]() is the unit ball.
is the unit ball.
For each $1 \le i\le N$![]() , consider the function $h_i:= f \circ \psi ^{-1} : V_i^+ \to {\mathbb {R}}$
, consider the function $h_i:= f \circ \psi ^{-1} : V_i^+ \to {\mathbb {R}}$![]() . We can estimate the modulus of continuity of each $h_i$
. We can estimate the modulus of continuity of each $h_i$![]() from above by the modulus of continuity of $f$
from above by the modulus of continuity of $f$![]() using the maximum bilipschitz constant of the $\psi _i$
using the maximum bilipschitz constant of the $\psi _i$![]() , which depends on $U$
, which depends on $U$![]() :
:
Note that $\omega _i$![]() is necessarily nondecreasing by definition. Since each $V_i^+$
is necessarily nondecreasing by definition. Since each $V_i^+$![]() is convex, $\omega _i$
is convex, $\omega _i$![]() is also subadditive, i.e. for all $r_1,\, r_2\ge 0$
is also subadditive, i.e. for all $r_1,\, r_2\ge 0$![]() ,
,
Moreover the uniform continuity of $f$![]() implies that
implies that
A direct application of [Reference Wells and Williams57, Theorem 13.16] implies that $h_i$![]() admits an extension $\tilde h_i$
admits an extension $\tilde h_i$![]() , given by
, given by
to the whole ${\mathbb {R}}^n$![]() also satisfying
also satisfying
Let $\{\theta _i\}_{0 \le i\le N}$![]() be a partition of unity corresponding to the covering $U_i$
be a partition of unity corresponding to the covering $U_i$![]() , i.e.
, i.e.

We extend $\theta _0 f :U_0 \to {\mathbb {R}}$![]() to $\tilde f_0:{\mathbb {R}}^n \to {\mathbb {R}}$
to $\tilde f_0:{\mathbb {R}}^n \to {\mathbb {R}}$![]() , and $\theta _i (\tilde h_i \circ \psi _i) : U_i \to {\mathbb {R}}$
, and $\theta _i (\tilde h_i \circ \psi _i) : U_i \to {\mathbb {R}}$![]() to $\tilde f_i: {\mathbb {R}}^n \to {\mathbb {R}}$
to $\tilde f_i: {\mathbb {R}}^n \to {\mathbb {R}}$![]() by the trivial zero extension and write
by the trivial zero extension and write

The conclusion follows.