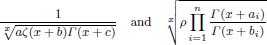Contents
Research Article
Minkowski Symmetry Sets of Plane Curves
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2016, pp. 461-480
-
- Article
- Export citation
On the Universal SL2-Representation Rings of Free Groups
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2017, pp. 973-1001
-
- Article
- Export citation
Applications of the Alexander Ideals to the Isomorphism Problem for Families of Groups
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2016, pp. 177-185
-
- Article
- Export citation
Theorems of the Phragmén–Lindelöf Type for Subfunctions in a Cone
- Part of:
-
- Published online by Cambridge University Press:
- 29 December 2016, pp. 739-751
-
- Article
- Export citation
Nilpotent, Algebraic and Quasi-Regular Elements in Rings and Algebras
- Part of:
-
- Published online by Cambridge University Press:
- 29 December 2016, pp. 753-769
-
- Article
- Export citation
Global Well-Posedness and Finite-Time Blow-Up of Some Heat-Type Equations
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 481-497
-
- Article
- Export citation
Multiple Spectra of Bernoulli Convolutions
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2016, pp. 187-202
-
- Article
- Export citation
Infinitely Many Solutions for Schrödinger–Kirchhoff-Type Fourth-Order Elliptic Equations
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2017, pp. 1003-1020
-
- Article
- Export citation
Periodic Navier Solutions for the Plate Equation with Non-Monotone Nonlinearities: the Multidimensional Case
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2016, pp. 203-230
-
- Article
- Export citation
The Applications of Critical-Point Theory to Discontinuous Fractional-Order Differential Equations
- Part of:
-
- Published online by Cambridge University Press:
- 16 March 2017, pp. 1021-1051
-
- Article
- Export citation
Factoriality and Type Classification of k-Graph von Neumann Algebras
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 499-518
-
- Article
- Export citation
A Fractal Operator on Some Standard Spaces of Functions
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2017, pp. 771-786
-
- Article
- Export citation
Equivariant Maps from Stiefel Bundles to Vector Bundles
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 231-250
-
- Article
- Export citation
Hyperbolic Metric and Multiply Connected Wandering Domains of Meromorphic Functions
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2017, pp. 787-810
-
- Article
- Export citation
Extremal Beltrami Differentials of Non-Landslide Type
- Part of:
-
- Published online by Cambridge University Press:
- 25 October 2016, pp. 519-526
-
- Article
- Export citation
Divisorial Models of Normal Varieties
- Part of:
-
- Published online by Cambridge University Press:
- 31 January 2017, pp. 1053-1064
-
- Article
- Export citation
Coexistence Solutions for a Periodic Competition Model with Singular–Degenerate Diffusion
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2016, pp. 1065-1075
-
- Article
- Export citation
Fischer Decomposition and Cauchy–Kovalevskaya Extension in Fractional Clifford Analysis: The Riemann–Liouville Case
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2016, pp. 251-272
-
- Article
- Export citation
Book Reviews
Antony G. O'Farrell and Ian Short, Reversibility in Dynamics and Group Theory, London Mathematical Society Lecture Notes Series, Volume 416 (Cambridge University Press, 2015), 294 pp., 978-1-107-44288-7 (paperback), £40.99.
-
- Published online by Cambridge University Press:
- 06 July 2017, pp. 811-812
-
- Article
- Export citation
Research Article
The Monotonicity and Log-Behaviour of Some Functions Related to the Euler Gamma Function
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2016, pp. 527-543
-
- Article
- Export citation
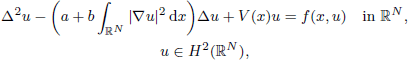
 be a single vertex
be a single vertex  be the von Neumann algebra induced from the Gelfand–Naimark–Segal (GNS) representation of a distinguished state
be the von Neumann algebra induced from the Gelfand–Naimark–Segal (GNS) representation of a distinguished state 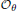 . In this paper we prove the factoriality of
. In this paper we prove the factoriality of  , the space of all real-valued continuous functions defined on a compact interval
, the space of all real-valued continuous functions defined on a compact interval 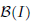 of all bounded functions and the Lebesgue space
of all bounded functions and the Lebesgue space 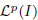 , and in some standard spaces of smooth functions such as the space
, and in some standard spaces of smooth functions such as the space 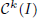 of
of 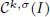 and Sobolev spaces
and Sobolev spaces 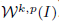 . Using properties of the
. Using properties of the 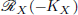 is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.
is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.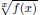 is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions
is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions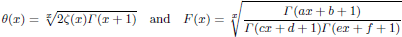
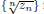 for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients
for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients 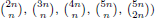 are demonstrated. In particular, this contains some results of Chen
are demonstrated. In particular, this contains some results of Chen 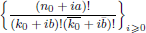
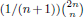 and the central binomial coefficients
and the central binomial coefficients 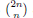 are infinitely log-monotonic, and strengthens one result of Su and Wang that
are infinitely log-monotonic, and strengthens one result of Su and Wang that 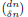 is log-convex in
is log-convex in