Contents
Research Article
The total curvature of a smooth closed curve in En is an upper bound to the total swing of its position vector
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 148-151
-
- Article
- Export citation
The volume of the intersection of a convex body with its translates
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 278-289
-
- Article
- Export citation
Decomposition of sets of small or large boundary
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 290-304
-
- Article
- Export citation
Corrigendum: On Vinogradov's mean value theorem
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 152
-
- Article
- Export citation
Book Reviews
W. A. Adkins and S. H. Weintraub. Algebra, An Approach via Module Theory. Springer. 1992, 526 pp., DM88. - V. I. Arnol'd. Singularities of Caustics and Wave Fronts. Kluwer. 1990, 259 pp., £56. - V. I. Arnol'd. Catastrophy Theory. Springer. 1992, 150 pp., DM 38. - D. K. Arrowsmith and C. M. Place. Dynamical Systems. Differential Equations, Maps and Chaotic Behaviour. Chapman & Hall. 1992, 330 pp., £17·95 - D. J. Bell. Mathematics of Linear and Nonlinear Systems—for Engineers and Applied Scientists. Clarendon Press. 1991, 304 pp., £16·50 - M. Bognár. Foundations of Linking Theory. Akadémiai Kiadó, Budapest. 1992, 164 pp., $20. - Y. A. Brychkov, H.-J. Glaeske, A. P. Prudnikov and Vu Kim Tuan. Multidimensional Integral Transformations. Gordon and Breach. 1992, 386 pp., £44. - C. K. Chui. An Introduction to Wavelets. Academic Press. 1992, 264 pp., $49.95. - C. K. Chui. Editor. Wavelets: a Tutorial in Theory and Applications. Academic Press. 1992, 713 pp., $69.95 - J. Dieudonné. Mathematics—the Music of Reason. Springer. 1992, 287 pp., DM 68. - P. Drábek. Solvability and Bifurcations of Nonlinear Equations. Longman. 1992, 227 pp., £25. - A. Dzhuraev. Degenerate and other Problems. Longman. 1992, 316 pp., £56. - A. Dzhuraev. Methods of Singular Integral Equations. Longman. 1992, 311 pp., £56. - R. Henstock. The General Theory of Integration. Clarendon Press. 1991, 262 pp., £40. - P. N. Hoffman and J. F. Humphreys. Projective Representations of the Symmetric Group, Q-functions and Shifted Tableaux. Clarendon Press. 1992, 304 pp., £40. - B. R. Gelbaum. Problems in Real and Complex Analysis. Springer. 1992, 488 pp., DM 118. - J. Gregory and C. Lin. Constrained Optimization in the Calculus of Variations and Optimal Control Theory. Van Nostrand Reinhold. 1992, 217 pp., £39. - G. R. Grimmett and D. R. Stirzaker. Probability and Random Processes, 2nd edition. Clarendon Press. 1992, 541 pp., £22·50. Probability and Random Processes: Problems and Solutions. Clarendon Press. 1991, 356 pp., £19·50. - A. R. Hall. Isaac Newton: Adventurer in Thought. Blackwell. 1992, 468 pp., £19·95. - P. M. Harman and A. E. Shapiro. Editors. The Investigation of Difficult Things: Essays on Newton and the History of the Exact Sciences. Cambridge University Press. 1992, 531 pp., £90 - G. G. Joseph. The Crest of the Peacock: non-European Roots of Mathematics. Penguin. 1992, 371 pp., £8·99. - Johannes Kepler. New Astronomy. Translated by W. H. Donohue. Cambridge. 1992, 665 pp., £85. - V. V. Kharchenko. Automorphisms and Derivations of Associative Rings. Kluwer. 1991, 385 pp., £88. - Li Ta-Tsien and Chen Yunmei. Global Classical Solutions for Nonlinear Evolution Equations. Longman. 1992, 209 pp., £47. - G. Micula and P. Pavel. Differential and Integral Equations through Practical Problems and Exercises. Kluwer. 1992, 395 pp., £82. - H.-O. Peitgen, H. Jürgens and D. Saupe. Chaos and Fractals. Springer. 1992, 984 pp., DM98. - L. W. Tung. Japanese/English, English/Japanese Glossary of Scientific and Technical Terms. Wiley. 1993, 1146 pp., £56. - P. Wesseling. An Introduction to Multigrid Methods. Wiley. 1992, 284 pp., £49.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-159
-
- Article
- Export citation
Research Article
Smooth bump functions and geomentry of Banach spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-321
-
- Article
- Export citation
Front matter
MTK volume 40 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Research Article
Estimates of spherial averages of Fourier transforms and dimensions of sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 322-330
-
- Article
- Export citation
Asymptotic behaviour of orthogonal polynomials relative to measures with mass points
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 331-344
-
- Article
- Export citation
Toeplitz and Hankel type operators on Bergman space
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 345-356
-
- Article
- Export citation
A sharp inequality related to Moser's inequality
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 357-366
-
- Article
- Export citation
The Hausdorff dimension of systems of simultaneously small linear forms
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 367-374
-
- Article
- Export citation
Book Reviews
A. M. Anile, J. K. Hunter, P. Pantano and G. Russo. Ray methods for nonlinear waves in fluids and plasmas. Longman. 1993, 243pp., £39. - K. Arczewski and J. Pietrucha. Mathematical Modelling of Mechanical Complex Systems. Ellis Horwood. 1993, 293 pp., £45. - T. A. Bick. Elementary Boundary Value Problems. Marcel Dekker. 1993, 264 pp., $49.75. - P. Biler and T. Nadzieja. Problems and examples in differential equations. Marcel Dekker. 1992, 264 pp., $55. - W. C. Brown. Matrices over Commutative Rings. Marcel Dekker. 1993, 281pp., $115. - B. Choudhary. The Elements of Complex Analysis. 2nd Edition. Wiley Eastern. 1992, 325 pp., 85 Rupees. - J. R. Clay. Nearrings, Geneses and Applications. Oxford University Press. 1992, 469 pp., £55. - H. Davenport. The Higher Arithmetic. 6th Edition. Cambridge University Press. 1992, 217 pp., £12·95. - G. Evans. Practical Numerical Integration. Wiley. 1993, 328 pp., £37·95. - A. Fassler and E. Stiefel. Group Theoretical Methods and their Applications. Birkhauser. 1992, 296 pp., 98SFr. - J. Fauvel, R. Flood and R. Wilson, Editors. Möbius and his Band: Mathematics and Astronomy in Nineteenth Century Germany. Oxford University Press. 1993, 172 pp., £19·50. - G. H. Hardy. A Mathematician's Apology. Cambridge University Press. 1992, 153 pp., £4·95. - B. Makarov, M. G. Goluzina, A. A. Lodkin and A. N. Podkorytov. Selected Problems in Real Analysis. American Mathematical Society, 1992, 371 pp., £78. - J. E. Marsden. Lectures on Mechanics. Cambridge University Press. 1992, 254 pp., £19.95. - D. S. Mitrinovic, J. E. Pecaric and A. M. Fink. Classical and New Inequalities in Analysis. Kluwer Academic. 1993, 740 pp., £170·50. - K. W. Morton and M. J. Baines, Editors. Numerical Methods for Fluid Dynamics III. Clarendon Press. 1988, 529 pp., £50. - J. E. Munro. Discrete Mathematics. Chapman & Hall. 1992, 306 pp., £16·95. - C. Nash. Differential Topology and Quantum Field Theory. Academic Press. 1991, 386 pp., £27. - E. R. Pinch. Optimal Control and the Calculus of Variations. Oxford University Press. 1993, 234 pp., £35. - S. C. Power. Limit Algebras: an Introduction to Subalgebras of C*-algebras. Longman Scientific & Technical. 1992, 201 pp., £23. - C. Reutenauer. Free Lie Algebras. LMS Monographs New Series, No. 7. Clarendon Press. 1993, 269 pp., £55. - H. Triebel. Higher Analysis. J. A. Barth. 1992, 473 pp., DM 148. - N. E. Wegge-Olsen. K-Theory and C*-algebras, a friendly approach. Oxford University Press. 1993, 370 pp., £35. - G. C. Wen. Conformal Mappings and boundary value problems. American Mathematical Society. 1992, 303 pp., £68. - Yau Chuen Wong. Introductory Theory of Topological Vector Spaces. Marcel Dekker. 1992, 440 pp., $59·75.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 375-380
-
- Article
- Export citation
Index
Index to Volume 40
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 381-382
-
- Article
- Export citation
Index to Volume 31–40
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 383-391
-
- Article
- Export citation
Front matter
MTK volume 40 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
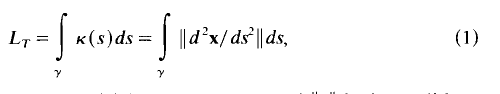

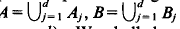 and vectors
and vectors 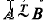 In [3], Theorem 3 we proved that if
In [3], Theorem 3 we proved that if 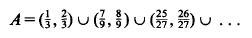
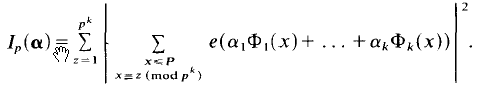
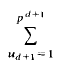
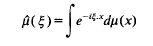
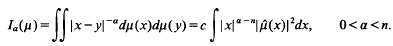
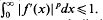 .
.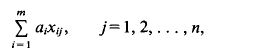

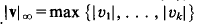 of any vector in
of any vector in