Article contents
Decomposition of sets of small or large boundary
Part of:
Combinatorics
Published online by Cambridge University Press: 26 February 2010
Extract
We shall say that the sets A, B ⊂ Rk are equivalent, if they are equidecomposable using translations; that is, if there are finite decompositions 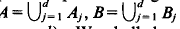 and vectors x1,…, xd∈Rk such that Bj = Aj + xj, (j = 1,…,d). We shall denote this fact by
and vectors x1,…, xd∈Rk such that Bj = Aj + xj, (j = 1,…,d). We shall denote this fact by 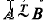 In [3], Theorem 3 we proved that if A ⊂ Rk is a bounded measurable set of positive measure then A is equivalent to a cube provided that Δ(δA)<k where δA denotes the boundary of A and Δ(E) denotes the packing dimension (or box dimension or upper entropy index) of the bounded set E. This implies, in particular, that any bounded convex set of positive measure is equivalent to a cube. C. A. Rogers asked whether or not the set
In [3], Theorem 3 we proved that if A ⊂ Rk is a bounded measurable set of positive measure then A is equivalent to a cube provided that Δ(δA)<k where δA denotes the boundary of A and Δ(E) denotes the packing dimension (or box dimension or upper entropy index) of the bounded set E. This implies, in particular, that any bounded convex set of positive measure is equivalent to a cube. C. A. Rogers asked whether or not the set
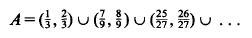
MSC classification
Secondary:
05A18: Partitions of sets
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1993
References
2.Kuipers, L. and Niederreiter, H.. Uniform distribution of sequences (John Wiley & Sons, 1974).Google Scholar
3.Laczkovich, M.. Decomposition of sets with small boundary. J. London Math. Soc., 46 (1992), 58–64.CrossRefGoogle Scholar
4.Schmidt, W.. Metrical theorems on fractional parts of sequences. Trans. Amer. Math. Soc., 110 (1964), 493–518.Google Scholar
5.Tricot, C. Jr. Two definitions of fractional dimension. Math. Proc. Cambridge Phil. Soc., 91 (1982), 5774.Google Scholar
- 4
- Cited by

