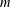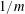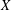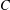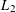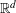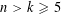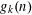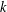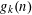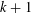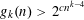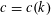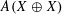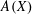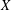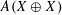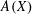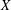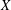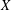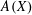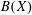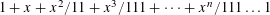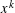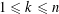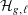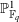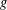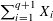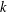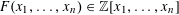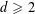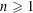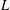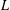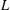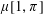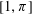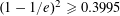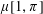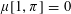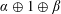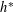Contents
Research Article
LONELY RUNNERS IN FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2019, pp. 677-701
-
- Article
- Export citation
FINITE FLAT SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1010-1017
-
- Article
- Export citation
THE ERDŐS–SZEKERES PROBLEM AND AN INDUCED RAMSEY QUESTION
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2019, pp. 702-707
-
- Article
- Export citation
INTERVALS BETWEEN CONSECUTIVE NUMBERS WHICH ARE SUMS OF TWO SQUARES
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1018-1032
-
- Article
- Export citation
EMBEDDING OF THE FREE ABELIAN TOPOLOGICAL GROUP
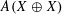 $A(X\oplus X)$ INTO
$A(X\oplus X)$ INTO 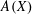 $A(X)$
$A(X)$
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2019, pp. 708-718
-
- Article
- Export citation
A CLASS OF IRREDUCIBLE POLYNOMIALS ASSOCIATED WITH PRIME DIVISORS OF VALUES OF CYCLOTOMIC POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1033-1037
-
- Article
- Export citation
ON THE DISTRIBUTION OF THE RATIONAL POINTS ON CYCLIC COVERS IN THE ABSENCE OF ROOTS OF UNITY
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2019, pp. 719-742
-
- Article
- Export citation
DENSITY OF POWER-FREE VALUES OF POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1038-1050
-
- Article
- Export citation
RANDOMNESS AND NON-RANDOMNESS PROPERTIES OF PIATETSKI-SHAPIRO SEQUENCES MODULO
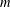 $m$
$m$
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1051-1073
-
- Article
- Export citation
A MEAN VALUE RESULT FOR A PRODUCT OF GL(2) AND GL(3)
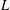 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2019, pp. 743-762
-
- Article
- Export citation
ZEROS OF THE MÖBIUS FUNCTION OF PERMUTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1074-1092
-
- Article
- Export citation
ARITHMETIC ASPECTS OF SYMMETRIC EDGE POLYTOPES
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2019, pp. 763-784
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MTK volume 65 Issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 September 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
A COUNTEREXAMPLE TO A CONJECTURE OF LARMAN AND ROGERS ON SETS AVOIDING DISTANCE 1
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2019, pp. 785-787
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MTK volume 65 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 June 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
MTK volume 65 Issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 06 September 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation
MTK volume 65 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 June 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation