Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Delucchi, Emanuele
and
Hoessly, Linard
2020.
Fundamental polytopes of metric trees via parallel connections of matroids.
European Journal of Combinatorics,
Vol. 87,
Issue. ,
p.
103098.
Ohsugi, Hidefumi
and
Tsuchiya, Akiyoshi
2020.
Reflexive polytopes arising from bipartite graphs with $$\gamma $$-positivity associated to interior polynomials.
Selecta Mathematica,
Vol. 26,
Issue. 4,
Athanasiadis, Christos A.
and
Tzanaki, Eleni
2021.
SYMMETRIC DECOMPOSITIONS, TRIANGULATIONS AND REAL‐ROOTEDNESS.
Mathematika,
Vol. 67,
Issue. 4,
p.
840.
Hibi, Takayuki
Lasoń, Michał
Matsuda, Kazunori
Michałek, Mateusz
and
Vodička, Martin
2021.
Gorenstein graphic matroids.
Israel Journal of Mathematics,
Vol. 243,
Issue. 1,
p.
1.
Ohsugi, Hidefumi
and
Tsuchiya, Akiyoshi
2021.
The $$h^*$$-Polynomials of Locally Anti-Blocking Lattice Polytopes and Their $$\gamma $$-Positivity.
Discrete & Computational Geometry,
Vol. 66,
Issue. 2,
p.
701.
Jochemko, Katharina
2022.
Symmetric Decompositions and the Veronese Construction.
International Mathematics Research Notices,
Vol. 2022,
Issue. 15,
p.
11427.
Chen, Tianran
and
Davis, Robert
2022.
A toric deformation method for solving Kuramoto equations on cycle networks.
Nonlinear Dynamics,
Vol. 109,
Issue. 3,
p.
2203.
Kálmán, Tamás
and
Tóthmérész, Lilla
2022.
Root polytopes and Jaeger‐type dissections for directed graphs.
Mathematika,
Vol. 68,
Issue. 4,
p.
1176.
Ostrovska, Sofiya
and
Ostrovskii, Mikhail I.
2022.
Isometric structure of transportation cost spaces on finite metric spaces.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 116,
Issue. 4,
Ohsugi, Hidefumi
and
Tsuchiya, Akiyoshi
2023.
PQ-Type Adjacency Polytopes of Join Graphs.
Discrete & Computational Geometry,
Vol. 70,
Issue. 1,
p.
214.
D’AlÌ, Alessio
Juhnke-Kubitzke, Martina
Köhne, Daniel
and
Venturello, Lorenzo
2023.
On the Gamma-Vector of Symmetric Edge Polytopes.
SIAM Journal on Discrete Mathematics,
Vol. 37,
Issue. 2,
p.
487.
Chen, Tianran
Davis, Robert
and
Korchevskaia, Evgeniia
2023.
Facets and facet subgraphs of symmetric edge polytopes.
Discrete Applied Mathematics,
Vol. 328,
Issue. ,
p.
139.
Kara, Selvi
Portakal, Irem
and
Tsuchiya, Akiyoshi
2023.
Rigid Gorenstein toric Fano varieties arising from directed graphs.
Collectanea Mathematica,
Vol. 74,
Issue. 2,
p.
333.
Becedas, Adrian
Kohn, Kathlén
and
Venturello, Lorenzo
2024.
Voronoi diagrams of algebraic varieties under polyhedral norms.
Journal of Symbolic Computation,
Vol. 120,
Issue. ,
p.
102229.
Tóthmérész, Lilla
2024.
A geometric proof for the root-independence of the greedoid polynomial of Eulerian branching greedoids.
Journal of Combinatorial Theory, Series A,
Vol. 206,
Issue. ,
p.
105891.
D’Alì, Alessio
Juhnke-Kubitzke, Martina
and
Koch, Melissa
2024.
On a Generalization of Symmetric Edge Polytopes to Regular Matroids.
International Mathematics Research Notices,
Vol. 2024,
Issue. 14,
p.
10844.
Kálmán, Tamás
and
Tóthmérész, Lilla
2024.
h * -vectors of graph polytopes using activities of dissecting spanning trees.
Algebraic Combinatorics,
Vol. 6,
Issue. 6,
p.
1637.
Davis, Robert
Jakovleski, Joakim
and
Pan, Qizhe
2024.
Normalized volumes of type-PQ adjacency polytopes for certain classes of graphs.
Involve, a Journal of Mathematics,
Vol. 17,
Issue. 3,
p.
425.
Jal, Aryaman
and
Jochemko, Katharina
2025.
Polyhedral combinatorics of bisectors.
Advances in Geometry,
Vol. 25,
Issue. 2,
p.
147.
Juhnke, Martina
Solus, Liam
and
Venturello, Lorenzo
2025.
Triangulations of cosmological polytopes.
Algebraic Combinatorics,
Vol. 8,
Issue. 4,
p.
1141.
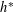 $h^{\ast }$-polynomial in case of complete bipartite graphs. In particular, we show that the
$h^{\ast }$-polynomial in case of complete bipartite graphs. In particular, we show that the 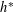 $h^{\ast }$-polynomial is
$h^{\ast }$-polynomial is  $\unicode[STIX]{x1D6FE}$-positive and real-rooted. This proves Gal’s conjecture for arbitrary flag unimodular triangulations in this case, and, beyond that, we prove a strengthening due to Nevo and Petersen [On
$\unicode[STIX]{x1D6FE}$-positive and real-rooted. This proves Gal’s conjecture for arbitrary flag unimodular triangulations in this case, and, beyond that, we prove a strengthening due to Nevo and Petersen [On 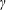 $\unicode[STIX]{x1D6FE}$-vectors satisfying the Kruskal–Katona inequalities. Discrete Comput. Geom.45(3) (2011), 503–521].
$\unicode[STIX]{x1D6FE}$-vectors satisfying the Kruskal–Katona inequalities. Discrete Comput. Geom.45(3) (2011), 503–521].
