Contents
Research Article
The resultant and the Koszul complex of a set of forms
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 348-356
-
- Article
- Export citation
Decomposition of flat manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-119
-
- Article
- Export citation
The linearity of wreath products
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 357-367
-
- Article
- Export citation
HB-subspaces and Godun sets of subspaces in Banach spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 120-132
-
- Article
- Export citation
Liouville properties on graphs
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-148
-
- Article
- Export citation
The number of blocks with a given defect group
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 368-373
-
- Article
- Export citation
The form of the spectral functions associated with Sturm-Liouville problems with continuous spectrum
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-161
-
- Article
- Export citation
Functional iterations and stopping times for Brownian motion on the Sierpiński gasket
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 374-400
-
- Article
- Export citation
On the asymptotic expansion of certain functions defined by infinite series
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 401-418
-
- Article
- Export citation
Triangulations of cyclic polytopes and higher Bruhat orders
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 162-194
-
- Article
- Export citation
The structure of Rabinowitz' global bifurcating continua for problems with weak nonlinearities
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 419-433
-
- Article
- Export citation
A Steiner type formula for convex functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 195-214
-
- Article
- Export citation
Covering convex bodies by translates of convex bodies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 215-218
-
- Article
- Export citation
Book-Reviews
G. Baumslag. Topics in Combinatorial Group Theory. Birkhauser. 1993, ISBN 3 7643 2921 1, (1993), 164 pp., 38 Swiss Francs. - L. Berggren, J. Borwein and P. Borwein, Editors. Pi: A Source Book. Springer. 1997, ISBN 0 387 94924 0; 716 pp., £38·50. - D. Berlinski. A Tour of the Calculus. Heinemann. 1996, ISBN 0 434 09844 2; 331 pp., paperback, £8·99. - M. R. Darnel. Theory of lattice-ordered groups. M. Dekker. 1995, ISBN 0 8247 9326 9; 539 pp., $165. - D. M. Evans, Editor. Model Theory of Groups and Automorphism Groups. L.M.S. Lecture Notes, 244. Cambridge University Press. 1997, ISBN 0 521 58955 X; 212 pp., paperback, £24·95. - W. Fulton. Young Tableaux: With Applications to Representation Theory and Geometry, L.M.S. Student Texts, 35. Cambridge University Press. 1997, ISBN 0 521 56724 6; 260 pp., paperback £14·95. - H. Groemer. Geometric Applications of Fourier Series and Spherical Harmonics. Cambridge University Press. 1996, ISBN 0 521 47318 7; 329 pp., hardback, £40. - W. Hodges. A shorter Model Theory. Cambridge University Press. 1997, ISBN 0 521 58713 1; 310 pp., paperback, £22·95. - M. N. Huxley. Area, Lattice Points and Exponential Sums. L.M.S. Monograph, New Series, 13. Clarendon Press. 1996, ISBN 0 19 853466 3; 494 pp., hardback, £85. - N. Jacobson. Finite-dimensional Division Algebras over Fields. Springer. 1996, ISBN 3 540 57029 2; 278 pp., £42·50. - D. L. Johnson. Presentations of Groups. L.M.S. Student Texts, 15, 2nd Edition. Cambridge University Press. 1997, ISBN 0 521 58542 2; 216 pp., paperback, £17·95. - D. Jungnickel and S. A. Vanstone, Editors. Coding Theory, Design Theory, Group Theory. Proceedings of the Marshall Hall Conference. J. Wiley. 1993, ISBN 0 471 55703 X; 299 pp., £71. - P.-L. Lions. Mathematical Topics in Fluid Mechanics, Vol. I, Incompressible Models. Clarendon Press. 1996, ISBN 0 19 851487 5; 237 pp., hardback, £29·50. - P. Lounesto. Clifford Algebras and Spinors, L.M.S. Lecture Notes, 239. Cambridge University Press. 1997, ISBN 0 521 59916 4; 306 pp., paperback, £27·95. - H. T. Nguyen and E. A. Walker. A first course in Fuzzy Logic. CRC Press, Boca Raton. 1977. ISBN 0 8493 9477 5; 266 pp., £49. - C. Peskine. An algebraic Introduction to Complex Projective Geometry, I. Commutative Algebra. Cambridge University Press. 1996, ISBN 0 521 48072 8; 230 pp., hardback, £25. - L. A. Petrosjan and V. V. Mazalov, Editors. Game Theory and Applications. Nova Science Publications. Vol. I, 1995, ISBN 1 56072 266 5; 219 pp., $79. Vol. II, 1996, ISBN 1 56072 390 4; 257 pp., $69. - L. Schneps and P. Lochak, Editors. Geometric Galois Action. Vol. 1, Around Grothendieck's Esquisse d'un Programme. Vol. 2, The Inverse Galois Problem, Moduli Spaces and Mapping Class Groups. L.M.S. Lecture Notes 242 and 243. Cambridge University Press. Vol. 1, 1997, ISBN 0 521 59642 4; 293 pp., paperback, £24'95. Vol. 2, 1997, ISBN 0 521 59641 6; 347 pp., £24·95. - J.-P. Serre. Galois cohomology. Springer. 1997, ISBN 3 540 61990 9; 210 pp., £32. - I. R. Shafarevich. Basic Notions of Algebra. Springer. 1997, ISBN 3 540 61221 1; 258 pp., paperback, £32. - A. C. Thompson. Minkowski Geometry. Cambridge University Press. 1996, ISBN 0 521 40472 X; 346 pp., hardback, £40. - T. A. Whitelaw. Introduction to Abstract Algebra. Blackie Academic & Professional. 1995, ISBN 0 7514 0147 1; 247 pp., paperback, £19·99.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 434-438
-
- Article
- Export citation
Book Reviews
M. Aschbacher. 3-Transposition Groups. Cambridge Tracts in Mathematics No. 124. Cambridge University Press. 1997, ISBN 0 521 57196 0, 260 pp., hardback, £35. - S. Axler. Linear Algebra done right. Springer. 1995, ISBN 0 387 94596 2, 238 pp. paperback, DM 40. - E. D. Bloch. A first course in Geometric Topology and Differential Geometry. Birkhäuser. 1997, ISBN 3 7643 3840 7, 421 pp., SFr 98. - J. F. Carlson. Modules and Group Algebras. Birkhäuser. 1996, ISBN 3 7643 5389 9, 91 pp., DM 34. - R. Carter, G. Segal and I. Macdonald. Lectures on Lie Groups and Lie Algebras. LMS Student Texts 32. Cambridge University Press. 1995, ISBN 0 521 49922 4, 190 pp., paperback, £13·95. - J. W. S. Cassels and E. V. Flynn. Prolegomina to a Middle-brow Arithmetic of Curves of Genus 2. Cambridge University Press. 1996, ISBN 0 521 48370 0, 219 pp., paperback, £24·95. - B. Fornberg. A Practical Guide to Pseudospectral Methods. Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press. 1996, ISBN 0 521 49582 2, 231 pp., £37·50. - B. V. Gnedenko and V. Y. Korolev. Random Summation: Limit Theorems and Applications. CRC Press. 1996, ISBN 0 8493 2875 6, 267 pp., $79.95. - I. Gratton Guinness. The Fontana History of the Mathematical Sciences. Fontana Press. 1997, ISBN 0 00 686179 2, 817 pp., paperback, £12·99. - E. Hernández and G. Weiss. A first course on Wavelets. CRC Press. 1996, ISBN 0 8493 8274 2, 489 pp., $64.95. - N. H. Ibragimov. Editor. Lie group analysis of differential equations. Vol. 3. New Trends in Theoretical Developments and Computational Methods. CRC Press. 1996, ISBN 0 8493 9419 8, 536 pp., $95. - T. W. Körner. The Pleasures of counting. Cambridge University Press. 1996, ISBN 0 521 56823 4, 534 pp., paperback, £17·95. - M. Machover. Set Theory, Logic and their Limitations. Cambridge University Press. 1996, ISBN 0 521 47998 3, 288 pp., paperback, £14·95. - I. Madsen and J. Tornehave. From Calculus to Cohomology. Cambridge University Press. 1997, ISBN 0 521 58956 8, 8, pp. paperback, £16·95. - C. Moeglin and J.-L. Waldspurger. Spectral Decomposition and Eisenstein Series. Cambridge University Press. 1995, ISBN 0 521 41893 3, 338 pp., £50. - C. E. Praeger and L. H. Soicher. Low Rank Representations and Graphs for Sporadic Groups. Australian Math. Soc. Lecture Series, No. 8. Cambridge University Press. 1997, ISBN 0 521 56737 8, 541 pp., paperback, £24·95. - D. Quinney and R. Harding. Calculus Connections, Vol. 1, A Multimedia Adventure. Wiley. 1996, Workbook ISBN 0 471 02111 3, 120 pp., and CD ISBN 0 471 01040, Workbook and CD, £22·50. - L. T. Rigatelli. Evariste Galois, 1811–1832. Birkhäuser. 1996, ISBN 0 8176 5410 0, 163, pp., paperback, SFr 32. - P. G. Saffman. Vortex Dynamics. Cambridge University Press. Reprinted 1995, ISBN 0 521 47739 5, 311 pp., paperback, £17·95. - A. D. Taylor. Mathematics and Politics, Strategy, voting, power and proof. Springer. 1995, ISBN 0 387 94391 9, 284 pp., paperback, £16. - G. Tenenbaum. Introduction to Analytic and Probabilistic Number Theory. Cambridge University Press. 1995, ISBN 0 521 41261 7, 448 pp., £45. - A. van der Poorten. Notes on Fermat's Last Theorem. Wiley. 1996, ISBN 0 471 06261 8, 222 pp., £35. - P. Wojtaszczyk. A mathematical introduction to Wavelets. Cambridge University Press. 1997, ISBN 0 521 57894 9, 261 pp., paperback, £13·95.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 219-224
-
- Article
- Export citation
Index
Index to Volume 44
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 439-440
-
- Article
- Export citation
Front matter
MTK volume 44 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
MTK volume 44 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation
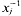 of degree - 1 be a formal inverse of
of degree - 1 be a formal inverse of 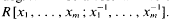 In [2, §2] we introduced a graded complex of
In [2, §2] we introduced a graded complex of 
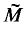 ×
× 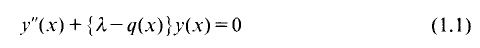
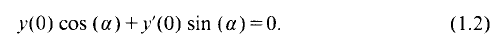
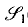 (
(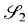 (
(