Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 3
KAKEYA-TYPE SETS IN LOCAL FIELDS WITH FINITE RESIDUE FIELD
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 614-629
-
- Article
- Export citation
- Cited by 3
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
-
- Article
- Export citation
- Cited by 3
Real classification of complex conics
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 36-53
-
- Article
- Export citation
- Cited by 3
MOVING STONE IN THE HELE-SHAW FLOW
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2015, pp. 457-474
-
- Article
- Export citation
- Cited by 3
A LIMITATION OF THE ESTIMATION OF INTRINSIC VOLUMES VIA PIXEL CONFIGURATION COUNTS
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2014, pp. 485-511
-
- Article
- Export citation
- Cited by 3
Transcendental numbers arising from Drinfeld modules
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 61-66
-
- Article
- Export citation
- Cited by 3
Isoperimetric problems for tilings
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-15
-
- Article
- Export citation
- Cited by 3
A property of the star domain |xy| ≤ 1
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 80
-
- Article
- Export citation
- Cited by 3
Continuous functions on products of compact Hausdorff spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 323-330
-
- Article
- Export citation
- Cited by 3
ARITHMETIC PROGRESSIONS IN SETS OF SMALL DOUBLING
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 587-613
-
- Article
- Export citation
- Cited by 3
On the distribution of gaps between squarefree numbers
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-101
-
- Article
- Export citation
- Cited by 3
Steady magnetohydrodynamic flow in an insulating circular pipe
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 249-262
-
- Article
- Export citation
- Cited by 3
A remark on Siegel's theorem on algebraic curves
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-127
-
- Article
- Export citation
- Cited by 3
Piatetski-Shapiro prime k-tuplets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 351-357
-
- Article
- Export citation
- Cited by 3
Projective representations of the infinite orthogonal group
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-121
-
- Article
- Export citation
- Cited by 3
On Minkowski reduction of positive quaternary quadratic forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 156-158
-
- Article
- Export citation
- Cited by 3
The fractional parts of a smooth sequence
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 292-296
-
- Article
- Export citation
- Cited by 3
On some axisymmetrical two sphere potential problems
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-70
-
- Article
- Export citation
- Cited by 3
The measure of the s-skeleton of a convex body
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 290-301
-
- Article
- Export citation
- Cited by 3
Surfaces with congruent shadow-lines
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-58
-
- Article
- Export citation
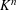
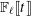
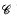 be a smooth projective, geometrically irreducible curve over a finite field
be a smooth projective, geometrically irreducible curve over a finite field 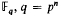 . We fix a rational point ∞on
. We fix a rational point ∞on 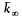 whose elements will be called “numbers”.
whose elements will be called “numbers”.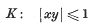
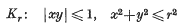
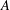
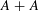
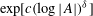
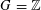
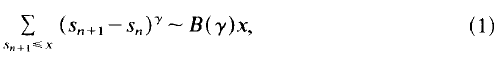
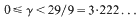
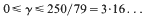
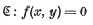
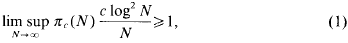
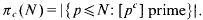
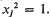

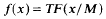
 -set [see 6] and it is therefore measurable with respect to the
-set [see 6] and it is therefore measurable with respect to the 