It is well known that, in the terminology of Moschovakis, Descriptive set theory (1980), every adequate normed pointclass closed under ∀ω has an effective version of the generalized reduction property (GRP) called the easy uniformization property (EUP). We prove a dual result: every adequate normed pointclass closed under ∃ω has the EUP. Moschovakis was concerned with the descriptive set theory of subsets of Polish topological spaces. We set up a general framework for parts of descriptive set theory and prove results that have as special cases not only the just-mentioned topological results, but also corresponding results concerning the descriptive set theory of classes of classes of structures.

Vaught (1973) asked whether the class of cPCδ classes of countable structures has the GRP. It does. A cPC(A) class is the class of all models of a sentence of the form , where ϕ is a sentence of ℒ∞ω that is in A and is a set of relation symbols that is in A. Vaught also asked whether there is any primitive recursively closed set A such that some effective version of the GRP holds for the class of cPC(A) classes of countable structures. There is: The class of cPC(A) classes of countable structures has the EUP if ω ∈ A and A is countable and primitive recursively closed. Those results and some extensions are obtained by first showing that the relevant classes of classes of structures, which Vaught showed normed, are in a suitable sense adequate and closed under ∃ω, and then applying the dual easy uniformization theorem.

For a structure let φ() be the number of nonisomorphic, countably infinite substructures of . The problem considered here, suggested by M. Pouzet, is that of characterizing those countable for which φ() ≤ ℵ0. In this paper we will deal exclusively with structures in a finite, binary relational language L. The characterization of those L-structures for which φ() ≤ ℵ0 (which turns out to be equivalent to ) is given in Theorem 3. It is the culmination of a three-step process. The first step, resulting in Theorem 1, shows that for a countable stable L-structure , φ() ≤ ℵ0 iff is cellular. (See Definition 0.1.) In the second step we consider linearly ordered sets = (A, ≤ ℵ0), and characterize in Theorem 2 the order types of those for which φ() ≤ ℵ0. Finally, in Theorem 3, we amalgamate Theorems 1 and 2 to get the classification of all countable L-structures for which φ() ≤ ℵ0.

The logic KM is the smallest normal modal logic that includes the McKinsey axiom

It is shown here that this axiom is not valid in the canonical frame for KM, answering a question first posed in the Lemmon-Scott manuscript [Lemmon, 1966].

The result is not just an esoteric counterexample: apart from interest generated by the long delay in a solution being found, the problem has been of historical importance in the development of our understanding of intensional model theory, and is of some conceptual significance, as will now be explained.

The relational semantics for normal modal logics first appeared in [Kripke, 1963], where a number of well-known systems were shown to be characterised by simple first-order conditions on binary relations (frames). This phenomenon was systematically investigated in [Lemmon, 1966], which introduced the technique of associating with each logic L a canonical frame which invalidates every nontheorem of L. If, in addition, each L-theorem is valid in , then L is said to be canonical. The problem of showing that L is determined by some validating condition C, meaning that the L-theorems are precisely those formulae valid in all frames satisfying C, can be solved by showing that satisfies C—in which case canonicity is also established. Numerous cases were studied, leading to the definition of a first-order condition Cφ associated with each formula φ of the form

where Ψ is a positive modal formula.

Let Γ be the unique (up to isomorphism) countable graph with the following property: (*) Given any two finite disjoint subsets U and V of Γ, there exists a vertex z ∈ Γ joined to every vertex in U and to none in V.

Thus Γ is the countable, universal, homogeneous graph; also known as the random graph. In this paper, we shall study the reducts of Γ Here a reduct of Γ is defined to be a permutation group (G, Γ) such that:

(i) Aut(Γ) ≤ G; and

(ii) G is a closed subgroup of Sym(Γ).

Equivalently, there exists a structure for some language L such that:

(iii) has universe Γ;

(iv) for each R ∈ L, is definable without parameters in Γ; and

(v) G = Aut().

In [12] Slaman and Steel posed the following problem:

Assume ZF + DC + AD. Suppose we have a function assigning to each Turing degree d a linear order <d of d. Then must the rationals embed order preservingly in <d for a cone of d's?

They had already obtained a partial answer to this question by showing that there is no such d ↦ <d with <d of order type ζ = ω* + ω on a cone. Already the possibility that <d has order type ζ · ζ was left open.

We use here, ideas and methods associated with the concept of amenability (of groups, actions, equivalence relations, etc.) to prove some general results from which one can obtain a positive answer to the above problem.

Let S be a recursive theory. Let a theory T* consisting of Σ1 sentences be called maximal (with respect to S) if T* is maximal consistent with S, i.e. there is no Σ1 sentence consistent with T* + S which is not in T*.

A maximal theory with respect to IΔ0 was considered by Wilkie and Paris in [WP] in connection with the end-extension problem.

Let us recall that IΔ0 is the fragment of Peano arithmetic consisting of the finite collection of algebraic axioms PA− together with the induction scheme restricted to bounded formulas.

The main open problem concerning the end-extendability of models of IΔ0 is the following:

(*) Does every model of IΔ0 + BΣ1 have a proper end-extension to a model of IΔ0?

Here BΣ1 is the following collection scheme:

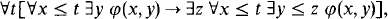
where φ runs over bounded formulas and may contain parameters.

It is well known(see [KP]) that if I is a proper initial segment of a model M of IΔ0, then I satisfies IΔ0 + BΣ1.

For a wide discussion of the problem (*) see [WP]. Wilkie and Paris construct in [WP] a model M of IΔ0 + BΣ1 which has no proper end-extension to a model of IΔ0 under the assumption IΔ0 ⊢¬Δ0 H (see [WP] for an explanation of this assumption). Their model M is a model of a maximal theory T* where S = IΔ0.

Moreover, T*, which is the set Σ1(M) of all Σ1 sentences true in M, is not codable in M.

Since its introduction in [K1-Po], the upper semilattice of Turing degrees has been an object of fascination to practitioners of the recursion-theoretic art. Starting from relatively simple concepts and definitions, it has turned out to be a structure of enormous complexity and richness. This paper is a contribution to the ongoing study of this structure.

Much of the work on Turing degrees may be formulated in terms of the embeddability of certain first-order structures in a structure whose universe is some set of degrees and whose relations, functions, and constants are natural degree-theoretic ones. Thus, for example, we know that if {P, ≤P) is a partial ordering of cardinality at most ℵ1 which is locally countable—each point has at most countably many predecessors—then there is an embedding

where D is the set of all Turing degrees and <T is Turing reducibility. If (P, ≤P) is a countable partial ordering, then the image of the embedding may be taken to be a subset of R, the set of recursively enumerable degrees. Without attempting to make the notion completely precise, we shall call embeddings of the first sort global, in contrast to local embeddings which impose some restrictions on the image set.

It is shown lhat no infinite group is interpretable in any structure which is homogeneous in a finite relational language. Related questions are discussed for other ω-categorical structures.

We generalize the ultrapower in a way suitable for choiceless set theory. Given an ultrafilter, forcing is used to construct an extended ultrapower of the universe, designed so that the fundamental theorem of ultrapowers holds even in the absence of the axiom of choice. If, in addition, we assume DC, then an extended ultrapower of the universe by a countably complete ultrafilter must be well-founded. As an application, we prove the Vopěnka-Hrbáček theorem from ZF + DC only (the proof of Vopěnka and Hrbáček used the full axiom of choice): if there exists a strongly compact cardinal, then the universe is not constructible from a set. The same method shows that, in L[2ω], there cannot exist a θ-compact cardinal less than θ (where θ is the least cardinal onto which the continuum cannot be mapped); a similar result can be proven for other models of the form L[A]. The result for L[2ω] is of particular interest in connection with the axiom of determinacy. The extended ultrapower construction of this paper is an improved version of the author's earlier pseudo-ultrapower method, making use of forcing rather than the omitting types theorem.

For countable structures and , let abbreviate the statement that every sentence true in also holds in . One can define a back and forth game between the structures and that determines whether . We verify that if θ is an Lω,ω sentence that is not equivalent to any Lω,ω sentence, then there are countably infinite models and such that ⊨ θ, ⊨ ¬θ, and . For countable languages ℒ there is a natural way to view ℒ structúres with universe ω as a topological space, Xℒ. Let [] = { ∊ Xℒ∣ ≅ } denote the isomorphism class of . Let and be countably infinite nonisomorphic ℒ structures, and let C ⊆ ωω be any subset. Our main result states that if , then there is a continuous function f: ωω → Xℒ with the property that x ∊ C ⇒ f(x) ∊ [] and x ∉ C ⇒ f(x) ∊ f(x) ∈ []. In fact, for α ≤ 3, the continuous function f can be defined from the relation.

It is shown that many different problems have the same degree of unsolvability. Among these problems are:

The Inductive Inference Problem. Infer in the limit an index for a recursive function f presented as f(0), f(1),f(2),….

The Recursive Index Problem. Decide in the limit if i is the index of a total recursive function.

The Zero Nonvariant Problem. Decide in the limit if a recursive function f presented as f(0), f(1), f(2),… has value unequal to zero for infinitely many arguments.

Finally, it is shown that these unsolvable problems are strictly easier than the halting problem.

Lachlan [5] has shown that it is not possible to embed the diamond lattice in the r.e. Turing degrees while preserving least and greatest elements; that is, there do not exist incomparable r.e. Turing degrees a and b such that a ∧ b = 0 and a ∨ b = 0′. Cooper [3] has compared the r.e. Turing degrees to the enumeration degrees below 0e′ and has asked if the two structures are elementarily equivalent.

In this paper we show that such an embedding is possible in the Σ2enumeration degrees, which implies a negative answer to Cooper's question.

Theorem. There are low enumeration degreesaandbsuch thata ∧ b = 0eanda ∨ b = 0e′.

Lower case italic letters denote elements of ω while upper case italic letters denote subsets of ω. D, E and F are reserved for finite sets, and K for ′. If D = {x0, x1, …, xn} then the canonical index of D is , and the canonical index of is ∅. Dx denotes the set with canonical index x. {Wi}i∈ω is any fixed standard listing of the r.e. sets, and <·, ·> is any fixed recursive bijection from ω × ω to ω.

Intuitively, A is enumeration reducible to B if there is an effective algorithm for producing an enumeration of A from any enumeration of B. There is a natural one-to-one correspondence between all such algorithms and the r.e. sets.

The purpose of this paper is an axiomatic study of the interrelations between certain continuity properties. We show that every mapping is sequentially continuous if and only if it is sequentially nondiscontinuous and strongly extensional, and that “every mapping is strongly extensional”, “every sequentially nondiscontinuous mapping is sequentially continuous”, and a weak version of Markov's principle are equivalent. Also, assuming a consequence of Church's thesis, we prove a version of the Kreisel-Lacombe-Shoenfield-Tseĭtin theorem.

In this paper, we show the normalization of proofs of NF (Quine's New Foundations; see [15]) minus extensionality. This system, called SF (Stratified Foundations) differs in many respects from the associated system of simple type theory. It is written in a first order language and not in a multi-sorted one, and the formulas need not be stratifiable, except in the instances of the comprehension scheme. There is a universal set, but, for a similar reason as in type theory, the paradoxical sets cannot be formed.

It is not immediately apparent, however, that SF is essentially richer than type theory. But it follows from Specker's celebrated result (see [16] and [4]) that the stratifiable formula (extensionality → the universe is not well-orderable) is a theorem of SF.

It is known (see [11]) that this set theory is consistent, though the consistency of NF is still an open problem.

The connections between consistency and cut-elimination are rather loose. Cut-elimination generally implies consistency. But the converse is not true. In the case of set theory, for example, ZF-like systems, though consistent, cannot be freed of cuts because the separation axioms allow the formation of sets from unstratifiable formulas. There are nevertheless interesting partial results obtained when restrictions are imposed on the removable cuts (see [1] and [9]). The systems with stratifiable comprehension are the only known set-theoretic systems that enjoy full cut-elimination.

We axiomatize all quantifier properties which can be expressed by a universal condition on the class of algebras of sets.

We consider the language L(Q), where L is a countable first-order language and Q is an additional generalized quantifier. A weak model for L(Q) is a pair 〈, q〉 where is a first-order structure for L and q is a family of subsets of its universe. In case that q is the set of classes of some equivalence relation the weak model 〈, q〉 is called a partition model. The interpretation of Q in partition models was studied by Szczerba [3], who was inspired by Pawlak's paper [2]. The corresponding set of tautologies in L(Q) is called rough logic. In the following we will give a set of axioms of rough logic and prove its completeness. Rough logic is designed for creating partition models.

The partition models are the weak models arising from equivalence relations. For the basic properties of the logic of weak models the reader is referred to Keisler's paper [1]. In a weak model 〈, q〉 the formulas of L(Q) are interpreted as usual with the additional clause for the quantifier Q: 〈, q〉 ⊨ Qx φ(x) iff there is some X ∊ q such that 〈, q〉 ⊨ φ(a) for all a ∊ X.

In case X satisfies the right side of the above equivalence we say that X is contained in φ(x) or, equivalently, φ(x) contains X.

We determine precisely those locally finite varieties of unary algebras of finite type which, when augmented by a ternary discriminator, generate a variety with a decidable theory.

We begin with some notes concerning the genesis of this paper. A preliminary version of it was written by the third author, who was moved by the desire to correct a mistake in Poizat [1987, p. 97], and to refresh some other minor results of the same book, concerning equations which are satisfied generically in a stable group. The book in question will be considered here as our basic reference on stable groups, and these other results will be discussed elsewhere.

This preliminary version contained §§1, 2 and 3 of the present paper, restricted to the context of groups of finite Morley rank. It was observed that a counterexample of finite rank to the above theorem would be an extreme refutation of a conjecture by Zil'ber and Cherlin (cyrillic alphabet order), that may be not so solid as was believed some time ago, which states that a simple group of finite rank should be an algebraic group. Additional motivation for the problem was seen in Reineke's theorem (Reineke [1975]), stating that a connected group of rank one is abelian—the cornerstone for the study of superstable groups—whose proof rests on the fact that a group with two conjugacy classes either has only two elements, or has infinite chains of centralizers (a property that violates stability).

We prove that every countably determined set C is U-meager if and only if every internal subset A of C is U-meager, provided that the cofinality and coinitiality of the cut U are both uncountable. As a consequence we prove that for such cuts a countably determined set C which intersects every U-monad in at most countably many points is U-meager. That complements a similar result in [KL]. We also give some partial solutions to some open problems from [KL]. We prove that the set , where H is an infinite integer, cannot be expressed as a countable union of countably determined sets each of which is U-meager for some cut U with min{cf(U), ci(U)} ≥ ω1. Also, every Borel, or countably determined set C which is U-meager for every cut U is a countable union of Borel, or countably determined sets respectively, which are U-nowhere dense for every cut U. Further, the class of Borel U-meager sets for min{cf(U),ci(U)} ≥ ω1 coincides with the least family of sets containing internal U-meager sets and closed with respect to the operation of countable union and intersection. The same is true if the phrase “U-meager sets” is replaced by “U-meager for every cut U.”

In this paper the existence or nonexistence of isomorphic mappings between graph models for the untyped lambda calculus is studied. It is shown that Engeler's is DA completely determined, up to isomorphism, by the cardinality of its ‘atom-set’ A. A similar characterization is given for a collection of graph models of the -type; from this some propositions regarding automorphisms are obtained. Also we give an indication of the complexity of the first-order theory of graph models by showing that the second-order theory of first-order definable elements of a graph model is first-order expressable in the model.