Article contents
Binary relational structures having only countably many nonisomorphic substructures
Published online by Cambridge University Press: 12 March 2014
Extract
For a structure 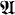 let φ(
let φ(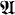 ) be the number of nonisomorphic, countably infinite substructures of
) be the number of nonisomorphic, countably infinite substructures of 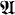 . The problem considered here, suggested by M. Pouzet, is that of characterizing those countable
. The problem considered here, suggested by M. Pouzet, is that of characterizing those countable 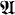 for which φ(
for which φ(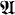 ) ≤ ℵ0. In this paper we will deal exclusively with structures in a finite, binary relational language L. The characterization of those L-structures for which φ(
) ≤ ℵ0. In this paper we will deal exclusively with structures in a finite, binary relational language L. The characterization of those L-structures for which φ(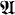 ) ≤ ℵ0 (which turns out to be equivalent to
) ≤ ℵ0 (which turns out to be equivalent to 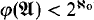 ) is given in Theorem 3. It is the culmination of a three-step process. The first step, resulting in Theorem 1, shows that for a countable stable L-structure
) is given in Theorem 3. It is the culmination of a three-step process. The first step, resulting in Theorem 1, shows that for a countable stable L-structure 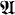 , φ(
, φ(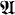 ) ≤ ℵ0 iff
) ≤ ℵ0 iff 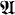 is cellular. (See Definition 0.1.) In the second step we consider linearly ordered sets
is cellular. (See Definition 0.1.) In the second step we consider linearly ordered sets 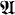 = (A, ≤ ℵ0), and characterize in Theorem 2 the order types of those
= (A, ≤ ℵ0), and characterize in Theorem 2 the order types of those 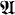 for which φ(
for which φ(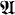 ) ≤ ℵ0. Finally, in Theorem 3, we amalgamate Theorems 1 and 2 to get the classification of all countable L-structures for which φ(
) ≤ ℵ0. Finally, in Theorem 3, we amalgamate Theorems 1 and 2 to get the classification of all countable L-structures for which φ(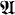 ) ≤ ℵ0.
) ≤ ℵ0.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1991
References
REFERENCES
- 2
- Cited by

