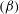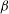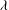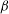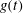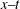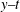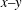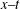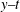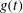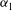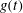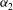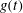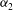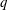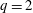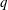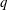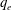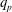Contents
Research Article
Solitary waves in asymmetric electron–positron–ion plasmas
-
- Published online by Cambridge University Press:
- 13 July 2015, 905810508
Nonlinear dust acoustic travelling waves in dusty plasmas due to dust charge fluctuations
-
- Published online by Cambridge University Press:
- 13 July 2015, 905810509
Nonlinear dynamics of ion acoustic waves in quantum pair-ion plasmas
-
- Published online by Cambridge University Press:
- 13 July 2015, 905810510
Theoretical analysis and simulation study on a coaxial vircator with enhanced modulation
-
- Published online by Cambridge University Press:
- 14 July 2015, 905810511
Generation of zonal flow and magnetic field in the ionospheric E-layer
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2015, 905810512
Turbulent dissipation challenge: a community-driven effort
-
- Published online by Cambridge University Press:
- 23 July 2015, 905810513
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service
Effect of the laser intensity profile on the shock non-uniformity in a directly driven spherical target
-
- Published online by Cambridge University Press:
- 29 July 2015, 905810514
Soliton-like solutions and chaotic motions for a forced and damped Zakharov–Kuznetsov equation in a magnetized electron–positron–ion plasma
-
- Published online by Cambridge University Press:
- 29 July 2015, 905810515
Effects of parallel sound wave damping and drift kinetic damping on the resistive wall mode stability with various plasma rotation profiles
-
- Published online by Cambridge University Press:
- 18 August 2015, 905810516
Nonlinear propagation of positron-acoustic waves in a four component space plasma
-
- Published online by Cambridge University Press:
- 20 August 2015, 905810517
Transverse instability of ion acoustic solitons in a magnetized plasma including
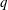 $q$ -nonextensive electrons and positrons
$q$ -nonextensive electrons and positrons
-
- Published online by Cambridge University Press:
- 04 September 2015, 905810518