Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Alam, M S
and
Talukder, M R
2020.
Head-on collision of ion-acoustic solitons in collisional pair ions plasmas with non-Maxwellian electrons.
Plasma Research Express,
Vol. 2,
Issue. 1,
p.
015014.
Deka, Manoj Kr.
and
Dev, Apul N.
2020.
Solitary Wave with Quantisation of Electron’s Orbit in a Magnetised Plasma in the Presence of Heavy Negative Ions.
Zeitschrift für Naturforschung A,
Vol. 75,
Issue. 3,
p.
211.
Mahmood, Shahzad
Ur‐Rehman, Hafeez
Ali, Munazza Zulfiqar
and
Basit, Abdul
2021.
Higher‐order inertial Alfvén wave dressed solitons, quasiperiodic structures, and chaos in plasmas.
Contributions to Plasma Physics,
Vol. 61,
Issue. 6,
Pradhan, Barsha
Saha, Asit
and
Natiq, Hayder
2021.
Multistability and dynamical properties of quantum ion-acoustic flow.
The European Physical Journal Special Topics,
Vol. 230,
Issue. 5,
p.
1503.
Baruah, Swati
Sarma, U.
and
Ganesh, R.
2021.
Effect of external magnetic field on lane formation in driven pair-ion plasmas.
Journal of Plasma Physics,
Vol. 87,
Issue. 2,
López, Álvaro G.
Ali, Rustam
Mandi, Laxmikanta
and
Chatterjee, Prasanta
2021.
Average conservative chaos in quantum dusty plasmas.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 31,
Issue. 1,
Pradhan, Barsha
Mukherjee, Sayan
Saha, Asit
Natiq, Hayder
and
Banerjee, Santo
2021.
Multistability and chaotic scenario in a quantum pair-ion plasma.
Zeitschrift für Naturforschung A,
Vol. 76,
Issue. 2,
p.
109.
Mandi, Laxmikanta
Natiq, Hayder
Chatterjee, Prasanta
Ali, Rustam
and
Banerjee, Santo
2021.
In search of hyperchaos in a high dimensional unmagnetized quantum plasma.
Zeitschrift für Naturforschung A,
Vol. 76,
Issue. 2,
p.
99.
Saha, Asit
Pradhan, Barsha
and
Natiq, Hayder
2022.
Multiperiodic and chaotic wave phenomena of collective ion dynamics under KP-type equation in a magnetised nonextensive plasma.
Physica Scripta,
Vol. 97,
Issue. 9,
p.
095604.
Kolay, Debaditya
Dutta, Debjit
and
Saha, Abhijit
2023.
Dynamics of ion-acoustic waves in multi-species quantum plasmas with arbitrary degeneracy.
Indian Journal of Physics,
Vol. 97,
Issue. 14,
p.
4465.
Pradhan, Barsha
Abdikian, Alireza
and
Saha, Asit
2025.
Nonlinear and supernonlinear ion-acoustic wave phenomena in an electron-positron-pair-ion quantum plasma.
Waves in Random and Complex Media,
Vol. 35,
Issue. 3,
p.
5432.
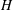 $H$ , positive to negative ion density ratio
$H$ , positive to negative ion density ratio 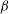 ${\it\beta}$ and Mach number on the nonlinear structures are investigated. It is found that these factors can significantly modify the properties of the IAWs. The existence of quasi-periodic and chaotic oscillations in the system is established. Switching from quasi-periodic to chaotic is possible with the variation of Mach number or quantum parameter
${\it\beta}$ and Mach number on the nonlinear structures are investigated. It is found that these factors can significantly modify the properties of the IAWs. The existence of quasi-periodic and chaotic oscillations in the system is established. Switching from quasi-periodic to chaotic is possible with the variation of Mach number or quantum parameter 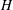 $H$ .
$H$ .
