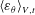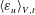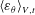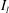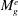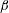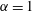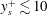Contents
Focus on Fluids
Deep learning in fluid dynamics
-
- Published online by Cambridge University Press:
- 31 January 2017, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
Modelling steady shear flows of Newtonian liquids with non-Newtonian interfaces
-
- Published online by Cambridge University Press:
- 31 January 2017, pp. 5-23
-
- Article
- Export citation
Viscosity effect on the longwave instability of a fluid interface subjected to horizontal vibrations
-
- Published online by Cambridge University Press:
- 02 February 2017, pp. 24-41
-
- Article
- Export citation
Temporally resolved measurements of heavy, rigid fibre translation and rotation in nearly homogeneous isotropic turbulence
-
- Published online by Cambridge University Press:
- 02 February 2017, pp. 42-68
-
- Article
- Export citation
Influence of slip on the three-dimensional instability of flow past an elongated superhydrophobic bluff body
-
- Published online by Cambridge University Press:
- 02 February 2017, pp. 69-94
-
- Article
- Export citation
Boundary-layer development and gravity waves in conventionally neutral wind farms
-
- Published online by Cambridge University Press:
- 06 February 2017, pp. 95-130
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical investigation of the water entry of cylinders without and with spin
-
- Published online by Cambridge University Press:
- 02 February 2017, pp. 131-164
-
- Article
- Export citation
Statistics of kinetic and thermal energy dissipation rates in two-dimensional turbulent Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 03 February 2017, pp. 165-184
-
- Article
- Export citation
One-dimensional refraction properties of compression shocks in non-ideal gases
-
- Published online by Cambridge University Press:
- 02 February 2017, pp. 185-221
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two-layer electrified pressure-driven flow in topographically structured channels
-
- Published online by Cambridge University Press:
- 02 February 2017, pp. 222-248
-
- Article
- Export citation
Small perturbation evolution in compressible Poiseuille flow: pressure–velocity interactions and obliqueness effects
-
- Published online by Cambridge University Press:
- 03 February 2017, pp. 249-276
-
- Article
- Export citation
Colliding drops as coalescing and fragmenting liquid springs
-
- Published online by Cambridge University Press:
- 03 February 2017, pp. 277-300
-
- Article
- Export citation
Effect of thermocapillary stress on slip length for a channel textured with parallel ridges
-
- Published online by Cambridge University Press:
- 06 February 2017, pp. 301-324
-
- Article
- Export citation
Near-critical swirling flow of a viscoelastic fluid in a circular pipe
-
- Published online by Cambridge University Press:
- 06 February 2017, pp. 325-360
-
- Article
- Export citation
Large eddy simulation of propeller wake instabilities
-
- Published online by Cambridge University Press:
- 06 February 2017, pp. 361-396
-
- Article
- Export citation
Curvature instability of a curved Batchelor vortex
-
- Published online by Cambridge University Press:
- 06 February 2017, pp. 397-415
-
- Article
- Export citation
Very-large-scale motions in rough-bed open-channel flow
-
- Published online by Cambridge University Press:
- 09 February 2017, pp. 416-429
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear proportional–integral control for skin-friction reduction in a turbulent channel flow
-
- Published online by Cambridge University Press:
- 08 February 2017, pp. 430-451
-
- Article
- Export citation
Droplet dynamics and fine-scale structure in a shearless turbulent mixing layer with phase changes
-
- Published online by Cambridge University Press:
- 08 February 2017, pp. 452-483
-
- Article
- Export citation
Optimal convection cooling flows in general 2D geometries
-
- Published online by Cambridge University Press:
- 08 February 2017, pp. 484-509
-
- Article
- Export citation