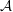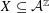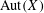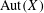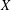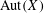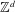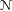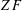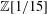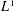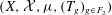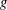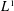Contents
Computational Mathematics
Research Article
THE HYPERBOLIC QUADRATIC EIGENVALUE PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 13 August 2015, e13
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
THE AUTOMORPHISM GROUP OF A SHIFT OF LINEAR GROWTH: BEYOND TRANSITIVITY
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2015, e5
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Research Article
ON THE IRREGULAR HODGE FILTRATION OF EXPONENTIALLY TWISTED MIXED HODGE MODULES
- Part of:
-
- Published online by Cambridge University Press:
- 25 May 2015, e9
-
- Article
-
- You have access
- Open access
- Export citation
Computational Mathematics
Research Article
DUAL EQUIVALENCE GRAPHS I: A NEW PARADIGM FOR SCHUR POSITIVITY
- Part of:
-
- Published online by Cambridge University Press:
- 22 July 2015, e12
-
- Article
-
- You have access
- Open access
- Export citation
Foundations
Research Article
ANALYTIC EQUIVALENCE RELATIONS SATISFYING HYPERARITHMETIC-IS-RECURSIVE
- Part of:
-
- Published online by Cambridge University Press:
- 27 April 2015, e8
-
- Article
-
- You have access
- Open access
- Export citation
Topology
Research Article
THE SHIMURA CURVE OF DISCRIMINANT 15 AND TOPOLOGICAL AUTOMORPHIC FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 05 February 2015, e3
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
FAILURE OF THE
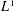 $L^{1}$ POINTWISE AND MAXIMAL ERGODIC THEOREMS FOR THE FREE GROUP
$L^{1}$ POINTWISE AND MAXIMAL ERGODIC THEOREMS FOR THE FREE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2015, e27
-
- Article
-
- You have access
- Open access
- Export citation
QUASIINVARIANT GAUSSIAN MEASURES FOR ONE-DIMENSIONAL HAMILTONIAN PARTIAL DIFFERENTIAL EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 02 December 2015, e28
-
- Article
-
- You have access
- Open access
- Export citation